[논문리뷰] TreeMeshGPT: Artistic Mesh Generation with Autoregressive Tree Sequencing

CVPR 2025. [Paper] [Github]
Stefan Lionar, Jiabin Liang, Gim Hee Lee
Sea AI Lab | Garena | National University of Singapore
14 Mar 2025

Introduction

MeshAnything은 MeshGPT에서 처음 제안한 메쉬 생성 Transformer에 포인트 클라우드 조건을 추가하여 3D 생성 기술과 아티스트 수준의 메쉬 생성 간의 격차를 메우고자 하였다. 포인트 클라우드는 고급 3D 생성 기법을 통해 생성된 Marching Cubes 메쉬에서 직접 출력되거나 편리하게 얻을 수 있기 때문에 조건으로 선택되었다.

MeshAnything은 각 삼각형 면을 9개의 latent 토큰으로 표현하기 때문에 시퀀스가 ​​길어지고, Transformer의 2차 복잡도로 인해 메쉬 생성은 800개의 면으로 제한된다. 이러한 제약은 복잡한 물체와 환경을 정확하게 표현하기 위해 훨씬 더 많은 면의 메쉬를 필요로 하는 실제 응용 분야에 어려움을 야기한다. MeshAnythingV2와 EdgeRunner는 삼각형 인접성을 활용하여 동일한 메쉬를 표현하는 더 짧은 시퀀스를 생성한다. 결과적으로 각각 최대 1,600개와 4,000개의 면을 가진 메쉬를 생성할 수 있다. 그러나 많은 실제 응용 분야에서는 세부적인 표면 토폴로지를 정확하게 표현하기 위해 더 많은 면의 메쉬를 요구한다. 또한, 유격, 누락된 부분, 뒤집힌 normal과 같은 아티팩트가 없는 고품질 메쉬를 생성하는 데는 여전히 어려움이 있다.

본 논문은 tokenization 효율성과 메쉬 품질을 더욱 향상시키기 위해 TreeMeshGPT를 도입했다. Transformer에서 next-token prediction에 의존하는 기존 방식과 달리, TreeMeshGPT는 새로운 Autoregressive Tree Sequencing 방식을 도입했다. 다음 토큰을 순차적으로 예측하는 대신, 본 방법은 메쉬 내 삼각형 인접성을 기반으로 동적으로 증가하는 트리 구조에서 다음 토큰을 검색한다. 이 전략을 통해 메쉬는 각 step에서 마지막으로 생성된 삼각형 면으로부터 로컬하게 확장되어 학습 난이도를 줄이고 메쉬 품질을 향상시킨다.

본 방법은 각 삼각형 면을 두 개의 토큰으로 표현하여, 면당 9개의 토큰을 사용하는 기존 면 tokenization 방식과 비교하여 22%의 압축률을 달성하였다. 이 효율적인 tokenization 기법은 메쉬 생성의 경계를 넓힌다. 7-bit discretization을 통해 2,048개의 토큰으로 구성된 강력한 포인트 클라우드 조건에서 최대 5,500개의 삼각형을 포함하는 메쉬를 생성할 수 있다. 또한, TreeMeshGPT는 강력한 normal 방향 제약을 갖는 메쉬를 생성하여 MeshAnything과 MeshAnythingV2에서 일반적으로 발생하는 반전된 normal을 최소화하였다.

Method

Tokenization은 autoregressive model, 특히 3D 메쉬 생성과 같은 복잡한 task에서 중요한 역할을 한다. Tokenization의 품질과 효율성은 모델 성능과 확장성에 큰 영향을 미친다. 메쉬 생성 맥락에서 tokenization은 꼭짓점, 모서리, 또는 면을 모델이 step별로 처리할 수 있는 순차적인 토큰으로 인코딩하는 것을 의미한다. 기존의 autoregressive한 메쉬 생성 방법은 각 출력을 다음 step의 입력으로 명시적으로 사용하는 next-token prediction 전략을 따랐다.

TreeMeshGPT는 생성 프로세스 동안 메쉬를 확장하기 위해 트리 기반 순회 방식을 사용한다는 점에서 다른 방식과 다르다. 특히, Transformer 디코더에 대한 입력은 방향이 있는 메쉬 모서리로,

\[\begin{equation} \textbf{I} = \{(v_1^n, v_2^n)\}_{n=1}^N \in \mathbb{R}^{N \times 6} \end{equation}\]

으로 표현된다. 각 $(v_1^n, v_2^n)$은 step $n$에서 생성을 위한 dequantize된 꼭짓점 쌍을 나타낸다. 각 step에서 Transformer 디코더는 메쉬를 확장하기 위해 초기 꼭짓점 쌍 $(v_1^n, v_2^n)$에 연결하여 새 꼭짓점 $v_3^n$을 추가하거나, 입력 모서리에서 더 이상 확장이 발생하지 않아야 함을 나타내는 [STOP] 레이블을 예측하는 로컬한 예측을 수행한다.

시퀀스 순서

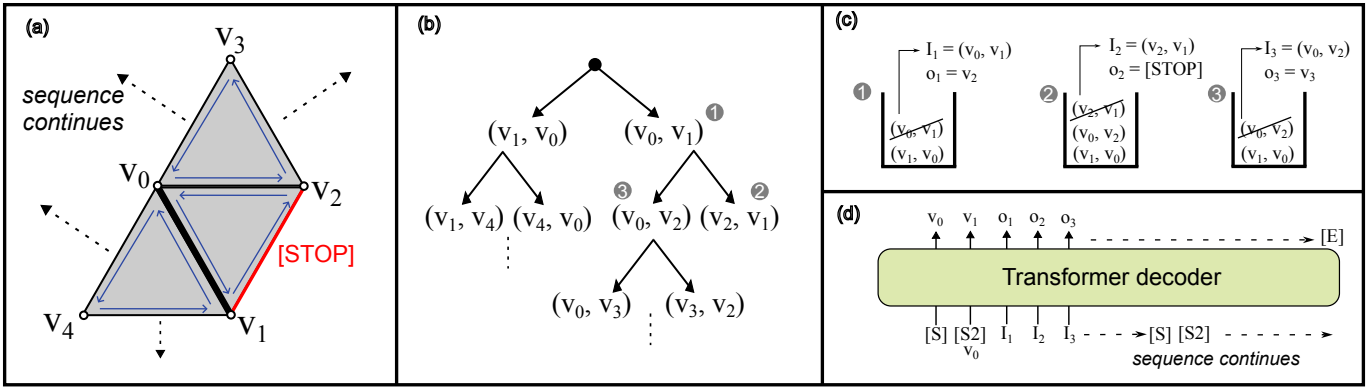
TreeMeshGPT는 트리 순회 프로세스를 활용하여 autoregressive한 생성을 위한 순차적 입력-출력 쌍 \((\textbf{I}, \textbf{O}) = \{(I_n, o_n)\}_{n=1}^N\)을 구성한다. 순차적 입력-출력 쌍을 구성하기 위해 DFS를 사용하는 half-edge 데이터 구조를 활용하는데, 순회 프로세스를 관리하기 위한 동적 stack $\textbf{S}$와 함께 사용된다.

순회 프로세스는 메쉬의 모서리에서 시작하며, 이 모서리에 삼각형을 형성하는 반대쪽 꼭짓점이 있는지, 경계인지, 또는 삼각형이 이미 방문되었는지 확인한다.

새로운 삼각형이 형성되면 반대쪽 꼭짓점 $v_3^n$이 출력으로 정의된다. $v_3^n$을 초기 모서리의 꼭짓점 $I_n = (v_1^n, v_2^n)$에 연결하여 두 개의 새로운 모서리가 생성되며, 그 결과 모서리 $(v_3^n, v_2^n)$와 $(v_1^n, v_3^n)$이 생성된다. 이러한 모서리는 잠재적으로 인접한 다음 면에 대해 반시계 방향으로 향한다. 새로 생성된 모서리는 계속적인 탐색을 위해 stack $\textbf{S}$에 push된다.

\[\begin{equation} \textbf{S} := \textbf{S} \odot (v_1^n, v_3^n) \quad \textrm{and} \quad \textbf{S} := \textbf{S} \odot (v_3^n, v_2^n) \end{equation}\]

($\odot$는 모서리 $(v_i, v_j)$를 stack $\textbf{S}$의 맨 위로 push하는 연산)

반대로, 입력 모서리가 경계이거나 새 꼭짓점을 추가하여 이전에 방문한 삼각형을 형성하는 경우, 출력은 [STOP] 레이블로 설정된다. 이 경우 새 꼭짓점이나 모서리가 추가되지 않는다.

다음 step인 $n+1$의 입력은 stack에서 맨 위 모서리를 pop하여 얻는다.

\[\begin{equation} I_{n+1} = (v_1^{n+1}, v_2^{n+1}) := \textrm{top} (\textbf{S}), \quad \textbf{S} := \textbf{S} \, \backslash \, \textrm{top} (\textbf{S}) \end{equation}\]

($\textrm{top}(\textbf{S})$는 stack $\textbf{S}$의 현재 가장 위에 있는 모서리를 가져오고, $\backslash$는 모서리 제거)

맨 처음에 stack은 메쉬의 가장 낮은 위치의 모서리으로 초기화된다 (모서리에 방향이 있으므로 2개가 stack에 포함됨). 그런 다음, 모든 삼각형을 방문할 때까지 순회가 진행된다.

메쉬는 여러 개의 연결 요소(connected component)로 구성될 수 있다. 연결 요소는 초기 모서리에서 시작하여 모서리가 stack에 추가됨에 따라 확장되고, stack이 비어 있으면 완전히 순회한 것으로 간주된다. 메쉬에 여러 연결 요소가 있는 경우, 첫 번째 연결 요소의 순회는 메쉬에서 가장 낮은 위치에 있는 모서리에서 시작하여 stack에 더 이상 모서리가 남지 않을 때까지 계속된다. 이후의 각 연결 요소는 나머지 방문하지 않은 면 중 가장 낮은 위치에 있는 모서리에서 시작한다.

생성 프로세스

메쉬 생성을 초기화하기 위해 보조 토큰 [SOS] $\in \mathbb{R}^D$를 입력으로 사용하여 첫 번째 꼭짓점 $v_1$을 예측한다. 다음 step에서는 $v_1$의 임베딩된 표현과 concat된 두 번째 보조 토큰 [SOS2] $\in \mathbb{R}^C$를 입력으로 사용하여 두 번째 꼭짓점 $v_2$를 예측한다. 초기 꼭짓점이 예측되면 메쉬 생성은 $(v_1, v_2)$와 $(v_2, v_1)$으로 초기화된 stack을 사용하는 Autoregressive Tree Sequencing을 진행한다. Stack이 비어 있으면, 즉 현재 연결 요소가 완료되면, [SOS] 토큰과 [SOS2] 토큰을 다시 추가하여 새 연결 요소를 초기화한다. 모든 연결 요소가 생성된 후 시퀀스는 [EOS] 레이블로 종료된다.

최종 메쉬는 초기 입력 꼭짓점 쌍과 예측된 반대 꼭짓점에서 형성된 면을 모아서 구성된다.

\[\begin{equation} \mathcal{M} = \bigcup_{n=1}^N (v_1^n, v_2^n, v_3^n) \\ \textrm{where} \; I_n \notin \{ [\textrm{SOS}], [\textrm{SOS2}] \}, \; o_n \notin \{ [\textrm{STOP}], [\textrm{EOS}] \} \end{equation}\]

입력 임베딩

각 꼭짓점을 고차원 공간에 인코딩하고 여러 주파수 기반에 걸쳐 위치 정보를 포착하기 위해 positional embedding을 사용한다. 이 임베딩 함수 \(\textrm{PosEmbed}(\cdot): \mathbb{R}^{3} \rightarrow \mathbb{R}^C\)는 3D 좌표를 $C$차원 임베딩에 매핑한다. 각 모서리에 대해 꼭짓점 쌍의 임베딩을 concat하여 $\mathbb{R}^{2C}$의 표현을 생성하고, 이후 MLP를 통해 Transformer의 hidden dimension인 $\mathbb{R}^D$에 매핑한다.

꼭짓점 예측

메쉬 생성에 관한 기존 방법들에서는 각 꼭짓점이 양자화된 $x$, $y$, $z$ 좌표에 해당하는 세 개의 토큰으로 구성된 시퀀스로 표현되었다. 특히, 하나의 꼭짓점 위치를 ​​예측하기 위해 이러한 모델은 각 좌표를 별도의 토큰으로 독립적으로 시퀀스에 생성한다. 이 방식은 각 꼭짓점에 세 개의 개별 토큰이 필요하므로 시퀀스가 ​​더 길어진다.

이와 대조적으로, 본 논문에서는 계층적 MLP head를 사용하여 꼭짓점의 quantize된 $x$, $y$, $z$ 좌표를 하나의 시퀀스 길이로 예측한다. 이 계층적 방식은 $x$, $y$, $z$ 좌표를 예측할 때 순차적인 특성을 유지하며, $x$, $y$, $z$ 좌표를 동시에 예측하는 예측 head에 비해 좌표 샘플링이 더 쉽다.

장점

Autoregressive Tree Sequencing은 트리 순회 과정에서 각 면이 두 개의 새로운 노드를 도입하기 때문에 삼각형 면당 두 개의 시퀀스 step만 추가한다. 또한 대부분의 메쉬는 적은 수의 연결 요소로만 구성되므로, 최소한의 보조 토큰만 사용한다. 이 효율적인 시퀀싱은 면당 9개의 토큰을 사용하는 단순 tokenization과 비교하여 대부분의 메쉬에서 약 22%의 압축률을 달성한며, MeshAnythingV2와 EdgeRunner의 약 두 배이다.

또한, 입력 시퀀스를 관리하기 위해 동적 stack을 사용함으로써, Transformer가 각 step에서 로컬한 예측에만 집중할 수 있도록 하여 학습 효율성을 향상시킨다. 더 나아가, 강력한 normal 방향 제약 조건을 갖는 메쉬를 생성하여 MeshAnything과 MeshAnythingV2에서 흔히 발생하는 뒤집힌 normal을 최소화한다.

Loss function

입력 시퀀스 \(\{I_n\}_{n=1}^N\)이 주어졌을 때 출력 시퀀스 \(\{o_n\}_{n=1}^N\)을 생성할 likelihood를 최대화하도록 Transformer 디코더 $\theta$를 학습시키는 것을 목표로 한다.

\[\begin{equation} \prod_{n=1}^N P (o_n \, \vert \, I_{\le n}; \theta) \end{equation}\]

이를 위해 모든 step에 걸쳐 teacher-forcing을 적용한다. GT 값 \(\textbf{O} = \{\textbf{O}_x, \textbf{O}_y, \textbf{O}_z\}\)와 예측 값 \(\hat{\textbf{O}} = \{\hat{\textbf{O}}_x, \hat{\textbf{O}}_y, \hat{\textbf{O}}_z\}\)는 특정 축을 따라 discretize된 꼭짓점 좌표를 나타내며, 각 좌표에 대한 cross-entropy loss들의 합으로 정의된 loss function을 사용한다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{CE} (\textbf{O}_x, \hat{\textbf{O}}_x) + \mathcal{L}_\textrm{CE} (\textbf{O}_y, \hat{\textbf{O}}_y) + \mathcal{L}_\textrm{CE} (\textbf{O}_z, \hat{\textbf{O}}_z) \end{equation}\]

정지 조건을 통합하기 위해, 높이 축의 클래스 선택에 [STOP] 레이블과 [EOS] 레이블을 추가하여 discretize된 좌표 클래스에 두 개의 클래스를 추가한다.

포인트 클라우드 컨디셔닝

메쉬 표면에서 8192개의 포인트 $\textbf{X} \in \mathbb{R}^{8192 \times 3}$를 샘플링한다. 그런 다음, cross-attention layer를 사용하여 각 포인트를 latent code $\textbf{Z}$로 만든다.

\[\begin{equation} \textbf{Z} = \textrm{CrossAtt} (\textbf{Q}, \textrm{PosEmbed} (\textbf{X})) \in \mathbb{R}^{2048 \times L} \end{equation}\]

($\textbf{Q} \in \mathbb{R}^{2048 \times C}$는 query 임베딩, $\textrm{PosEmbed}$는 Autoregressive Tree Sequencing과 동일한 임베딩 함수)

$\textbf{Z}$는 포인트 클라우드 컨디셔닝을 위해 첫 번째 [SOS] 토큰 앞에 추가된다.

Experiments

• 데이터셋: Objaverse
  • 모든 메쉬는 $[-0.5, 0.5]^3$으로 정규화
  • 7-bit discretization 적용, 중복 삼각형 제거, 5,500개보다 적은 수의 면을 가진 메쉬만 선택
  • 직각 투영(orthographic projection) 후, 하나의 투영된 넓이가 다른 것보다 매우 작으면 해당 메쉬를 선택하지 않음
  • data augmentation
    • scaling: 각 축을 독립적으로 [0.75, 0.95] 범위에서 샘플링
    • rotation: 먼저 $x$축 또는 $y$축을 따라 90° 또는 -90° 회전을 0.3의 확률로 적용한 후, [-180°, 180°]에서 균일하게 샘플링된 각도로 $z$축을 중심으로 회전
• 아키텍처 디테일
  • layer 24개, attention head 16개, hidden dimension 1024
  • latent code 조건에는 full self-attention, 디코더는 causal self-attention
  • positional embedding 차원: $C$ = 512
  • 좌표 클래스 수: 128 (7-bit quantization)
• 학습 디테일
  • optimizer: AdamW
  • learning rate: $10^{-4}$
  • effective batch size: 128
  • GPU: 학습은 A100-80GB 8개로 약 5일 소요

1. Results on Objaverse Dataset

다음은 Objaverse 데이터셋에서의 비교 결과이다.

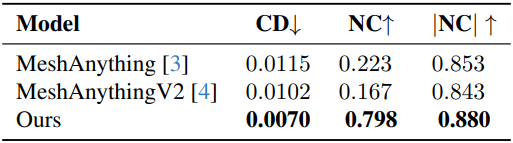
다음은 tokenizer를 제외한 모든 요인을 동일하게 설정하고 tokenizer의 영향을 비교한 표이다.

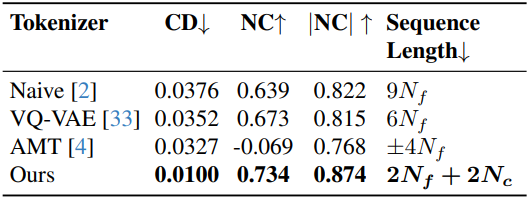
2. Results on GSO Dataset

다음은 Objaverse 데이터셋에서의 비교 결과이다.

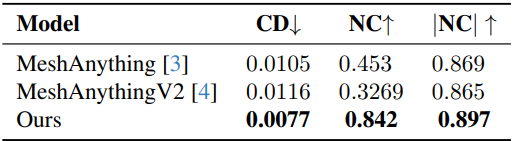
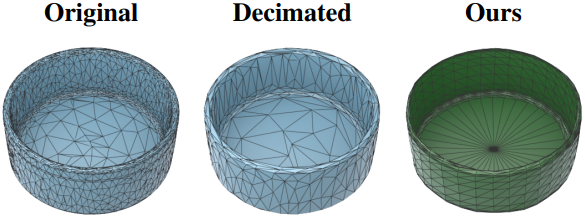
다음은 원본mesh decimation으로 면의 개수를 줄인 메쉬와 비교한 결과이다.

3. Ablation Study

다음은 MLP head에 대한 ablation 결과이다.

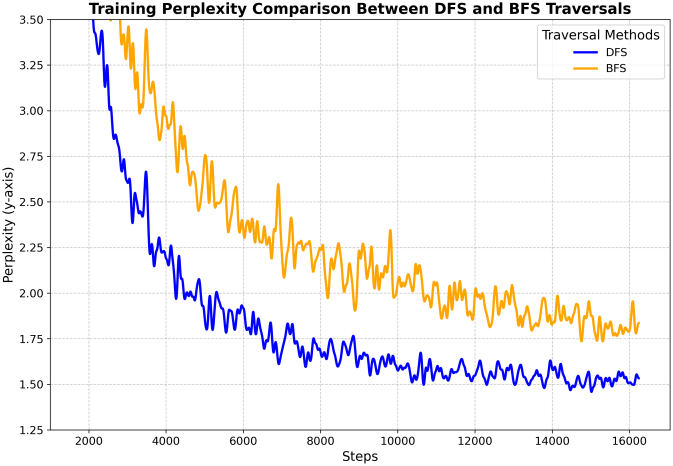
다음은 트리 순회 방법에 대한 ablation 결과이다. (DFS vs. BFS)

Limitations

1. 시퀀스 길이가 증가함에 따라 성공률이 감소한다.
2. 최적의 메쉬 토폴로지를 구현하는 데에는 여전히 어려움이 있다.