[논문리뷰] Semi-Implicit Denoising Diffusion Models (SIDDMs)
arXiv 2023. [Paper]
Yanwu Xu, Mingming Gong, Shaoan Xie, Wei Wei, Matthias Grundmann, kayhan Batmanghelich, Tingbo Hou
Google | Boston University | The University of Melbourne | Carnegie Mellon University
21 Jun 2023
Introduction
생성 모델은 다양한 영역에서 상당한 성공을 거두었으며, 특정 문제를 해결하기 위해 다양한 유형의 생성 모델이 개발되었다. VAE는 명시적인 목적 함수를 가진 학습 모델에 대한 변형 하한 (VLB)을 제공한다. GAN은 min-max 게임 프레임워크를 도입하여 암시적으로 데이터 분포를 모델링하고 one-step 생성을 가능하게 한다. Score 기반 생성 모델이라고도 하는 DDPM은 초기 랜덤 Gaussian noise 벡터에서 반복적인 denoising을 통해 원래 데이터 분포를 복구한다. 그러나 이러한 모델은 고품질 샘플링, 모드 커버리지, 빠른 샘플링 속도를 동시에 보장하는 것과 관련된 “TRILEMMA“로 알려진 일반적인 문제에 직면해 있다. GAN, VAE, DDPM과 같은 기존 접근 방식은 세 가지 측면을 모두 동시에 해결하는 데 어려움을 겪고 있다. 본 논문에서는 이러한 TRILEMMA 문제를 해결하고 대규모 데이터 생성을 효과적으로 모델링할 수 있는 모델을 개발하는 데 중점을 둔다.
Diffusion model은 VAE에 비해 고품질 샘플을 생성하는 데 탁월하고 GAN보다 더 나은 학습 수렴을 보여주지만 일반적으로 최고 품질의 결과를 얻으려면 수천 번의 반복 step이 필요하다. 이러한 긴 샘플링 step은 forward diffusion process에서 noise 추가가 작을 때 reverse diffusion 분포가 가우시안 분포에 의해 근사될 수 있다는 가정을 기반으로 한다. 그러나 noise 추가가 중요하면 reverse diffusion 분포가 non-Gaussian multimodal 분포가 된다. 결과적으로 더 빠른 생성을 위해 샘플링 step의 수를 줄이면 이 가정을 위반하고 생성된 샘플에 편향을 도입할 수 있다.
이 문제를 해결하기 위해 DDGAN은 forward diffusion 샘플링의 재구성을 제안하고 조건부 GAN을 사용하여 정의되지 않은 denoising 분포를 모델링한다. 이 접근 방식을 사용하면 생성된 샘플의 품질을 손상시키지 않고 더 빠르게 샘플링할 수 있다. 또한 DDGAN은 일반 GAN에 비해 학습 중에 향상된 수렴과 안정성을 나타낸다. 그러나 DDGAN은 여전히 ImageNet과 같은 다양한 대규모 데이터셋을 생성하는 데 한계가 있다. 저자들은 인접한 단계에서 변수의 공동 분포를 캡처하는 암시적 적대적 학습의 효과가 제한적이라는 가설을 제안하였다. 이 제한은 discriminator가 인접한 변수의 고차원 concatenation에서 작동해야 한다는 사실에서 발생하며 이는 어려울 수 있다.
빠른 샘플링 속도와 대규모 데이터셋 생성 능력을 달성하기 위해 Semi-Implicit Denoising Diffusion Model (SIDDM)이라는 새로운 접근 방식을 도입했다. SIDDM은 diffusion model의 denoising 분포를 재구성하고 암시적 및 명시적 목적 함수를 통합한다. 구체적으로 denoising 분포를 두 가지 구성 요소로 분해한다.
- Noisy하게 샘플링된 데이터의 주변 분포
- 조건부 forward diffusion 분포
이러한 구성 요소는 각 diffusion step에서 denoising 분포를 공동으로 공식화한다. SIDDM은 암시적 GAN 목적 함수와 명시적 L2 재구성 loss를 최종 목적 함수로 사용한다. 암시적 GAN 목적 함수는 주변 분포에 적용되는 반면 명시적 L2 재구성 loss는 조건부 분포에 적용된다. 여기에서 조건부 분포를 일치시키는 프로세스를 목적 함수에서 Auxiliary Forward Diffusion (AFD)로 명명한다. 이 조합은 DDGAN에 비해 추가 계산 오버헤드를 도입하지 않고도 우수한 학습 수렴을 보장한다. 모델의 생성 품질을 더욱 향상시키기 위해 discriminator에 Unet 모양의 구조를 통합한다. 또한 보조 denoising task를 포함하는 새로운 정규화 기술을 도입한다. 이 정규화 방법은 추가 계산 부담 없이 discriminator의 학습을 효과적으로 안정화한다.
Semi-Implicit Denoising Diffusion Models
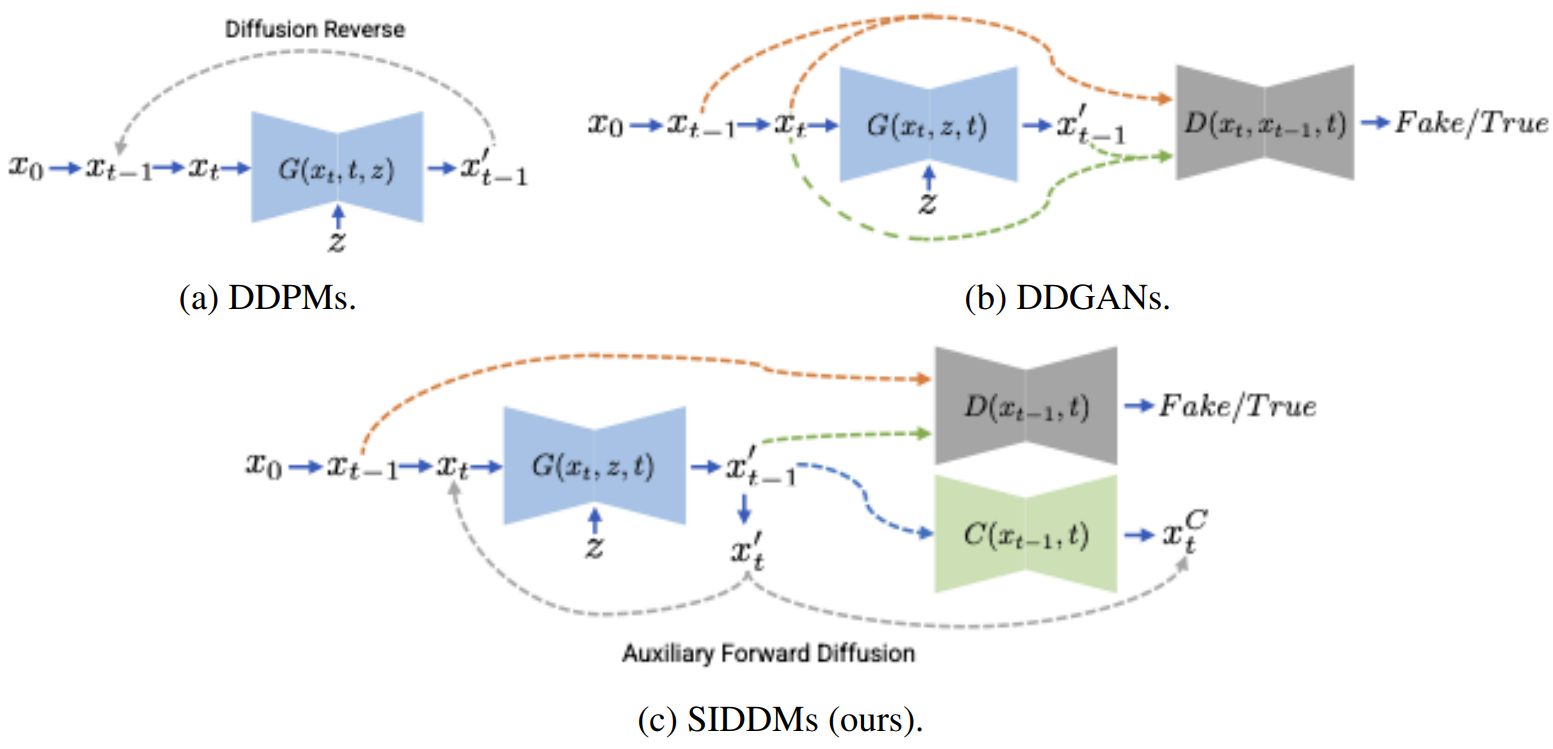
1. Revisiting Denoising Distribution and the Improved Decomposition
DDGAN의 목적 함수는 다음과 같다.
\[\begin{aligned} \min_\theta \max_{D_\phi} \sum_{t > 0} \mathbb{E}_{q(x_0) q(x_{t-1} \vert x_0) q(x_t \vert x_{t-1})} & [[-\log (D_\phi (x_{t-1}, x_t, t))] \\ &\;+ \mathbb{E}_{p_\theta (x_{t-1} \vert x_t)} [-\log (1 - D_\phi (x_{t-1}, x_t, t))]] \end{aligned}\]이는 다음과 같이 재구성될 수 있다.
\[\begin{equation} \min_\theta \max_{D_\textrm{adv}} \mathbb{E}_{q(x_0) q(x_{t-1} \vert x_0) q(x_t \vert x_{t-1})} D_\textrm{adv} (q(x_{t-1}, x_t) \| p_\theta (x_{t-1}, x_t)) \end{equation}\]여기서 DDGAN의 공식은 $q(x_{t−1}, x_t)$와 $p_\theta (x_{t−1}, x_t)$ 사이의 결합 분포를 일치시켜 통해 두 분포의 조건부 분포를 간접적으로 일치시킨다.
이것으로부터 시작하여 역방향으로 두 개의 결합 분포를 인수 분해하여
\[\begin{equation} q(x_{t−1}, x_t) = q(x_t \vert x_{t-1})q(x_{t−1}) \\ p_\theta (x_{t−1}, xt) = p_\theta (x_t \vert x_{t-1}) p_\theta (x_{t-1}) \end{equation}\]를 얻는다. 조건부 분포는 forward diffusion이며, 분포 일치 목적 함수에서 Auxiliary Forward Diffusion (AFD)라고 부른다. 이 분해에서 denoise된 데이터 $q(x_{t−1})$, $p_\theta (x_{t−1})$의 주변 분포 쌍과 조건부 분포 $q(x_t \vert x_{t-1})$, $p_\theta (x_t \vert x_{t-1})$ 쌍을 가진다. 주변 분포에는 명시적 형식이 없기 때문에 적대적 학습을 통해 Jensen-Shannon divergence (JSD)를 최소화하여 암시적으로 일치시킬 수 있다. Forward diffusion의 조건부 분포의 경우 $q(x_t \vert x_{t-1})$은 명시적인 가우시안 형식을 가지므로 KL을 통해 일치시킬 수 있다. 다음 정리는 이 두 쌍의 분포를 개별적으로 일치시키면 결합 분포와 대략적으로 일치할 수 있음을 나타낸다.
Theroem 1 $q(x_{t-1}, x_t)$와 $p_\theta (x_{t-1}, x_t)$가 각각 denoiser $G_\theta$에 의해 지정된 forward diffusion과 denoising 분포로부터의 데이터 분포를 나타낸다고 하자. 그러면 다음과 같은 부등식이 성립한다.
\[\begin{aligned} \textrm{JSD} (q (x_{t-1}, x_t), p_\theta (x_{t-1}, x_t)) & \le 2 c_1 \sqrt{2 \textrm{JSD} (q(x_{t-1}), p_\theta (x_{t-1}))} \\ & + 2 c_2 \sqrt{2 \textrm{KL} (p_\theta (x_t \vert x_{t-1}) \| q (x_t \vert x_{t-1}))} \end{aligned}\]여기서 $c_1$과 $c_2$는 각각 $\frac{1}{2} \int \vert q(x_t \vert x_{t-1}) \vert \mu (x_{t-1}, x_t)$와 $\frac{1}{2} \int \vert p(x_{t-1}) \vert \mu (x_{t-1})$의 상한이다 ($\mu$는 $\sigma$-finite measure).
2. Semi-Implicit Objective
위의 분석을 기반으로 SIDDM 분포 일치 목적 함수를 다음과 같이 쓸 수 있다.
\[\begin{aligned} \min_\theta \max_{D_\textrm{adv}} \mathbb{E}_{q(x_0) q(x_{t-1} \vert x_0) q (x_t \vert x_{t-1})} & [D_\textrm{adv} (q(x_{t-1}) \| p_\theta (x_{t-1})) \\ & + \lambda_\textrm{AFD} \textrm{KL} (p_\theta (x_t \vert x_{t-1}) \| q(x_t \vert x_{t-1}))] \end{aligned}\]여기서 \(\lambda_\textrm{AFD}\)는 AFD의 일치를 위한 가중치이다. 위 식에서 적대적 부분 \(D_\textrm{adv}\)는 표준 GAN 목적 함수이다. KL을 통해 AFD의 분포를 일치시키기 위해 다음과 같이 확장할 수 있다.
\[\begin{aligned} \textrm{KL} (p_\theta (x_t \vert x_{t-1}) \| q(x_t \vert x_{t-1})) &= \int p_\theta (x_t \vert x_{t-1}) \log p_\theta (x_t \vert x_{t-1}) - \int p_\theta (x_t \vert x_{t-1}) \log q(x_t \vert x_{t-1}) \\ &= -H (p_\theta (x_t \vert x_{t-1})) + H (p_\theta (x_t \vert x_{t-1}), q(x_t \vert x_{t-1})) \end{aligned}\]이는 $p_\theta (x_t \vert x_{t-1})$의 음의 엔트로피와 $p_\theta (x_t \vert x_{t-1})$과 $q(x_t \vert x_{t-1})$ 사이의 cross entropy의 결합이다. Cross entropy 항을 최적화하는 것은 평균 제곱 오차 (MSE)를 사용하여 경험적 분포와 가우시안 분포 사이의 cross entropy를 쉽게 나타낼 수 있기 때문에 간단하다. 이는 forward diffusion $q(x_t \vert x_{t-1})$이 가우시안 분포를 따르기 때문에 가능하다.
그러나 음의 엔트로피 항은 다루기 어렵다. 하지만 $p_\theta (x_t \vert x_{t-1})$은 $p_\theta (x_{t-1} \vert x_t)$를 모델링하는 denoiser $G$의 샘플에서 추정할 수 있다. 따라서 $−H(p_\theta (x_t \vert x_{t-1}))$를 대략적으로 계산하기 위해 또 다른 분포 $p_\psi (x_t \vert x_{t-1})$이 필요하다.
조건부 엔트로피의 최대화는 다음과 같은 적대적 목적 함수에 의해 근사화될 수 있다.
\[\begin{equation} \min_\theta \max_\psi \mathbb{E}_{p_\theta (x_t \vert x_{t-1})} \log p_\psi (x_t \vert x_{t-1}) \end{equation}\]이 식은 최대화 step과 최소화 step을 분리하여 고려하면 쉽게 증명할 수 있다. 먼저 $p_\theta$를 고정하면 다음과 같이 된다.
\[\begin{equation} \max_\psi \mathbb{E}_{p_\theta (x_t \vert x_{t-1})} \log p_\psi (x_t \vert x_{t-1}) = \max_\psi - H (p_\theta (x_t \vert x_{t-1}), p_\psi (x_t \vert x_{t-1})) \end{equation}\]$p_\theta (x_{t-1} \vert x_t) = p_\psi (x_t \vert x_{t-1})$일 때 음의 cross entropy가 최대가 된다.
최소화 step의 경우 $\psi$를 고정하면 다음과 같이 된다.
\[\begin{aligned} \min_\theta \mathbb{E}_{p_\theta (x_t \vert x_{t-1})} \log p_\psi (x_t \vert x_{t-1}) &= \min_\theta - H (p_\theta (x_t \vert x_{t-1}), p_\psi (x_t \vert x_{t-1})) \\ &= \min_\theta - H (p_\theta (x_t \vert x_{t-1})) \end{aligned}\]따라서 generator $p_\theta$와 조건부 estimator $p_\psi$ 사이의 이 반복적인 min-max 게임은 $−H(p_\theta (x_t \vert x_{t-1}))$를 최소화할 수 있다. 이 적대적 프로세스는 $p_\psi (x_t \vert x_{t-1})$에 대한 likelihood에 액세스할 수 있는 한 수행할 수 있다. 본 논문의 경우 forward diffusion이며 가우시안 분포를 따른다.
DDGAN과 비슷하게, 사후 확률 분포를 통해
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) := q(x_{t-1} \vert x_t, x_0 = G_\theta (x_t, t)) \end{equation}\]로 정의한다. 분포 일치 목적 함수에서 GAN을 적용하여 주변 분포의 JSD를 최적화하고, $L_2$ reconstruction을 적용하여 cross entropy를 최적화한다. 또한 \(x'_{t-1}\)을 새로 정의된 분포에서 샘플링된 데이터로 정의하고, forward diffusion을 통해 \(x'_{t-1}\)에서 \(x'_t\)를 샘플링한다.
전체 목적 함수는 아래와 같다.
\[\begin{aligned} \min_\theta \max_{D_\phi, C_\psi} \sum_{t > 0} \mathbb{E}_{q (x_0) q(x_{t-1} \vert x_0) q(x_t \vert x_{t-1})} & \bigg[ [-\log (D_\phi (x_{t-1}, t))] + [-\log (1 - D_\phi (x'_{t-1}, t))] \\ &+ \lambda_\textrm{AFD} \frac{(1 - \beta_t) \| x'_{t-1} - x_{t-1} \|^2 - \| C_\psi (x'_{t-1}) - x'_t \|^2}{\beta_t} \bigg] \end{aligned}\]여기서 $C_\psi$는 음의 조건부 엔트로피를 최소화하는 방법을 배우는 회귀 모델이다. 구현에서 discriminator와 회귀 모델 간에 가장 많은 레이어를 공유한다.
DDGAN과 비교할 때, SIDDM은 순전히 적대적인 목적 함수를 포기하고 이를 주변 분포와 하나의 조건부 분포로 분해한다. 여기서 조건부 분포는 덜 복잡한 목적 함수로 최적화될 수 있으며 denoising 모델 업데이트를 위한 안정적인 학습으로 이어진다. SIDDM은 DDPM과 동일한 모델 구조를 공유하고 고급 DDPM 네트워크 구조를 기반으로 개선될 수 있다. 또한 본 논문의 분해는 DDGAN에 비해 어떤 오버헤드도 가져오지 않으며 꾸준한 성능 향상을 달성할 수 있다.
3. Regularizer of Discriminator
UnetGAN은 생성된 샘플에서 더 자세한 정보를 보여주기 위해 discriminator에 Unet 구조를 채택할 것을 제안하였다. “True/Fake”의 글로벌 binary logit만 출력하는 discriminator의 일반적인 디자인과 달리 Unet 모양의 discriminator는 다른 레벨에서 디테일을 구별할 수 있다. Diffusion model의 denoising process는 픽셀 레벨 분포 일치의 이점을 얻을 수도 있다. 따라서 denoiser $G_\theta$와 discriminator $D_\phi$ 사이에 동일한 네트워크 구조를 공유한다. 분해 공식에서 영감을 얻은 reconstruction 항은 더 나은 기울기 추정을 제공하고 모델 성능을 향상시킨다. 또한 독립적으로 discriminator에 동일한 전략을 적용한다. 즉, discriminator에서 denoising 출력을 가져와서 ground-truth $x_0$로 재구성한다. 다음과 같이 regularizer를 공식화한다.
\[\begin{equation} \min_{D_\phi} \mathbb{E}_{q(x_0) q(x_{t-1} \vert x_0)} L_2 (D_\phi (x_{t-1}, t), x_0) \end{equation}\]여기서 이 정규화는 샘플링된 데이터 $q(x_t)$에만 적용된다. 일반적으로 사용되는 spectral norm과 달리 이 정규화는 모델 용량 제한과 같은 부작용을 가져오지 않아 추가 오버헤드 또는 각 데이터셋에서 hyperparameter의 grid search가 필요하다. Regularizer는 모델과 DDGAN에 쉽게 연결할 수 있으며 GAN으로 diffusion model을 강화하기 위해 특별히 설계된 추가 네트워크 설계가 필요하지 않다.
Experiments
- 데이터셋: Mixture of Gaussians (MOG), CIFAR10-32, CelebA-HQ-256, ImageNet1000-64
- 구현 디테일
- 아키텍처는 ADM과 같이 Unet 적용
- Imagen과 동일하게 Unet 블록의 다운샘플링 레이어와 업샘플링 레이어의 순서를 변경
- Discriminator도 Unet 사용
1. MOG Synthetic Data
다음은 5$\times$5 Mixture of Gaussians의 생성 결과이다.

다음은 5$\times$5 Mixture of Gaussians의 FID를 비교한 표이다.

2. Generation on Real Data
다음은 CIFAR10에서 생성된 샘플이다.

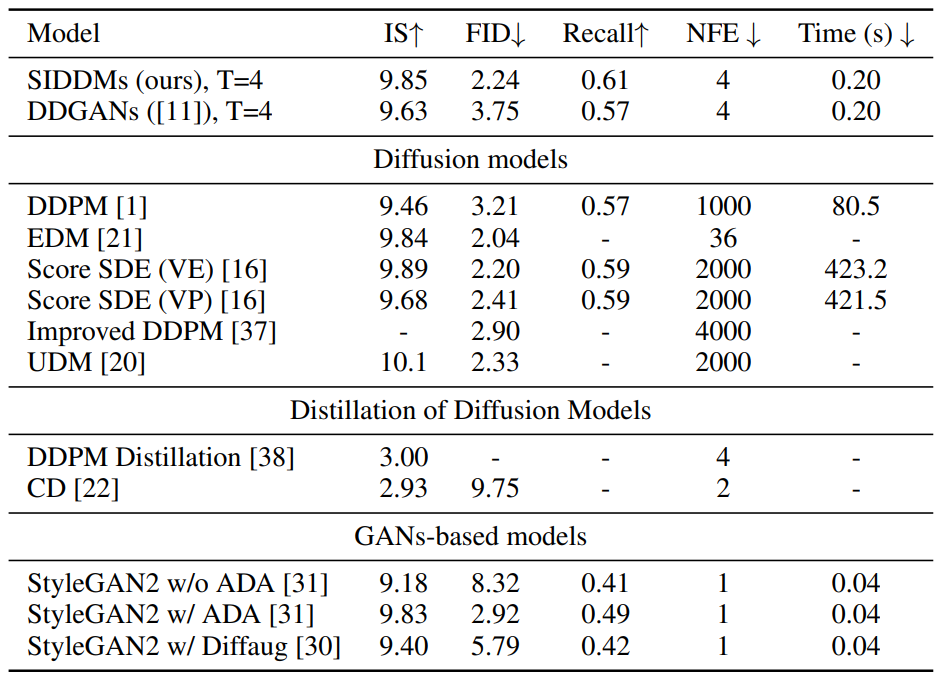
다음은 CIFAR10에서의 생성 결과를 비교한 표이다.
다음은 CelebHQ에서 생성된 샘플이다.

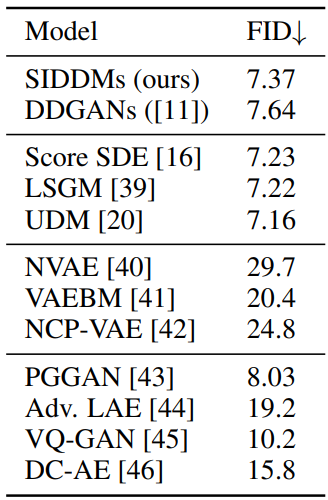
다음은 CelebHQ에서의 생성 결과를 비교한 표이다.
다음은 ImageNet에서 생성된 샘플이다.
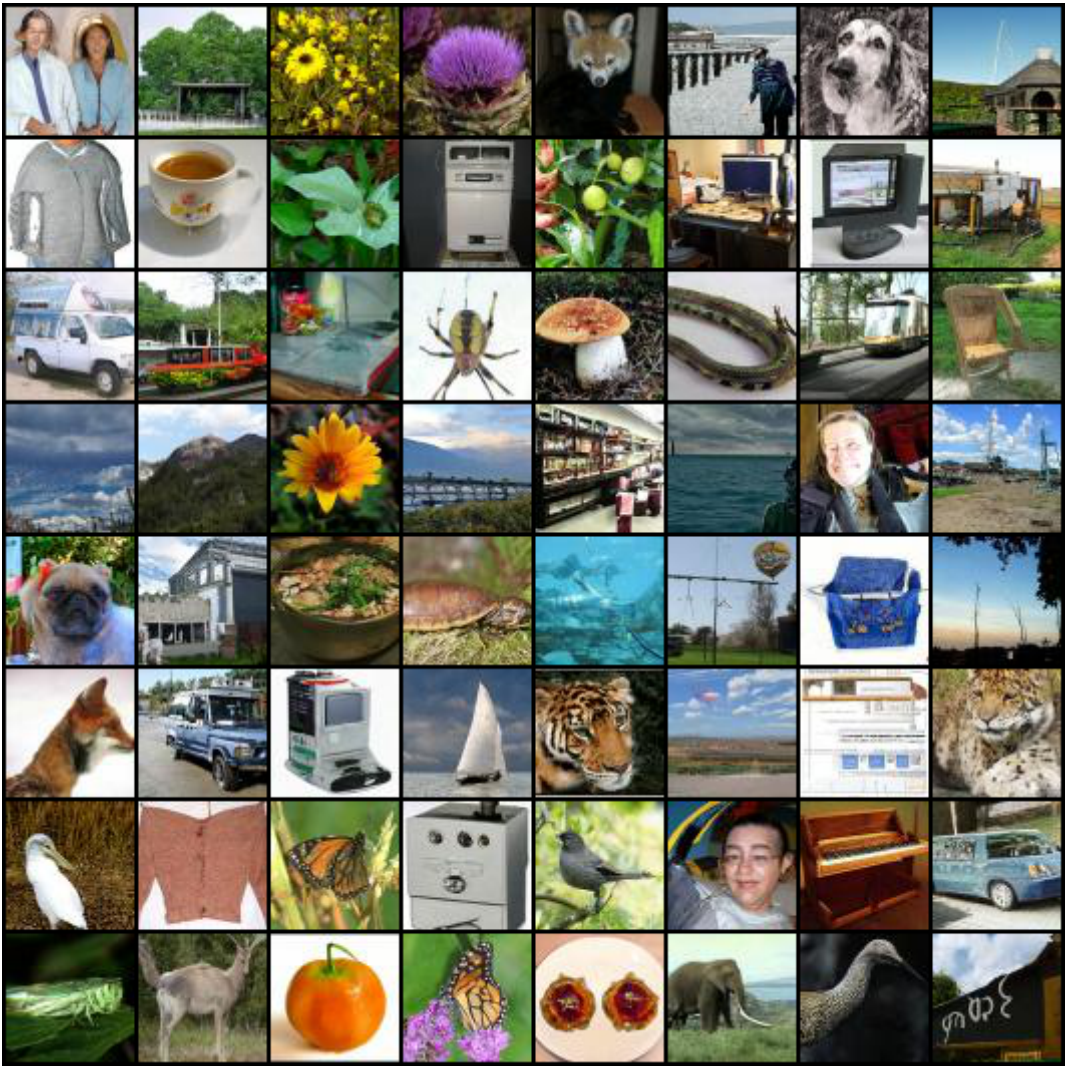
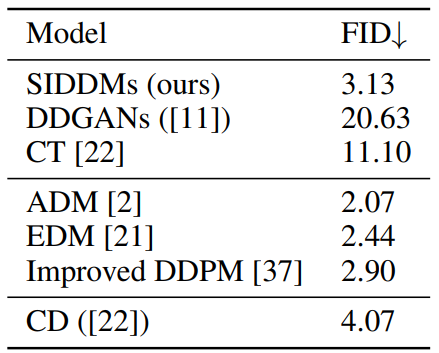
다음은 ImageNet에서의 생성 결과를 비교한 표이다.
Ablations
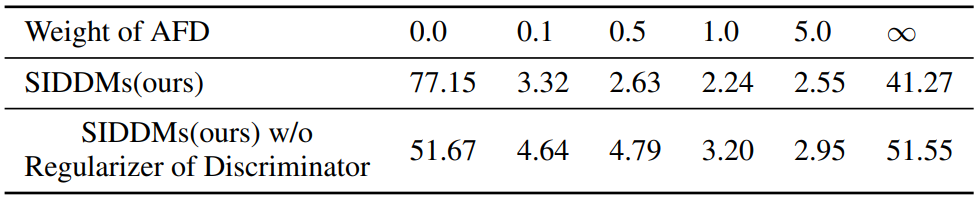
다음은 AFD 가중치에 따른 샘플들이다.

다음은 AFD 가중치에 따른 성능 변화를 나타낸 표이다.
다음은 diffusion step에 따른 성능 변화를 나타낸 표이다.
