[논문리뷰] Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
ICLR 2022 (Spotlight). [Paper] [Page] [Github]
Zhisheng Xiao, Karsten Kreis, Arash Vahdat
The University of Chicago | NVIDIA
15 Dec 2021
Introduction
현재의 생성 학습 프레임워크는 실제 문제에서 널리 적용되는 데 필요한 세 가지 주요 요구 사항을 동시에 충족할 수 없다.
- 고품질 샘플링
- 모드 커버리지와 샘플의 다양성
- 빠르고 계산 비용이 저렴한 샘플링
기존 모델은 일반적으로 이러한 요구 사항 사이에서 타협하기 때문에 문제가 발생하며, 이를 생성 학습 트릴레마(generative learning trilemma)라 한다.
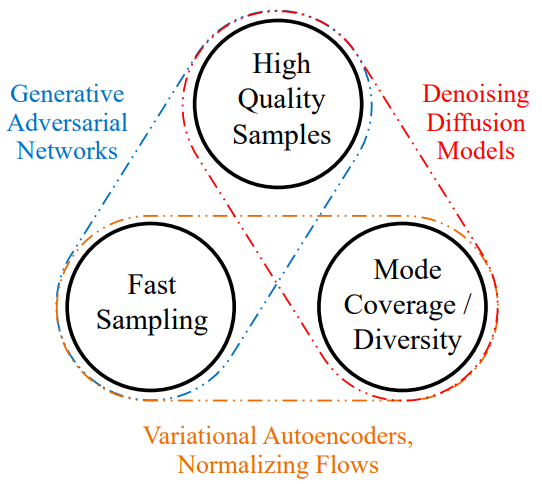
위 그림은 주류 생성 프레임워크가 트릴레마를 해결하는 방법을 요약한 것이다. GAN은 고품질 샘플을 빠르게 생성하지만 모드 커버리지가 나빠 mode collapse가 발생하기 쉽다. VAE와 normalizing flow는 모드 커버리지가 좋지만 샘플의 품질이 떨어진다. 최근 강력한 생성 모델로 떠오르고 있는 diffusion model은 이미지 생성 분야에서 GAN보다 좋은 성능을 보였으며, 모드 커버리지도 좋다. 하지만 샘플링에 수 천번 신경망을 돌려야 하므로 오래 걸린다.
본 논문에서는 강력한 모드 커버리지와 샘플 품질을 유지하면서 샘플링을 빠르게 하기 위해 denoising diffusion model을 재구성하여 생성 학습 트릴레마를 해결한다. Diffusion model의 느린 샘플링 문제를 조사한 결과 일반적으로 denoising 분포가 가우시안 분포에 의해 근사될 수 있다고 가정한다는 것을 관찰하였다. 그러나 가우시안 분포 가정은 denoising step의 무한소 극한에서만 유지되는 것으로 알려져 있으며, reverse process에서 많은 수의 step이 필요하다. Reverse process가 더 큰 step 크기를 사용하는 경우 (즉, denoising step이 더 적음) denoising 분포를 모델링하기 위해 non-Gaussian multimodal 분포가 필요하다. 이미지 합성에서 multimodal 분포는 여러 개의 그럴듯한 깨끗한 이미지가 동일한 noise 이미지에 해당할 수 있다는 사실을 기반으로 한다.
여기에서 영감을 받아 큰 step에 대한 denoising을 가능하게 하는 표현적인 multimodal 분포로 denoising 분포를 parameterize할 것을 제안한다. 특히, denoising 분포가 조건부 GAN으로 모델링되는 denoising diffusion GAN이라는 새로운 생성 모델을 도입한다. 이미지 생성에서 본 논문의 모델이 diffusion model에 비해 경쟁력 있는 샘플 품질과 모드 커버리지를 얻음과 동시에 2개의 denoising step만 수행하여 CIFAR-10에서 predictor-corrector sampling에 비해 샘플링에서 약 2000배의 속도 향상을 달성하였다. 기존의 GAN과 비교하여 본 논문의 모델은 샘플 다양성에서 state-of-the-art GAN보다 훨씬 뛰어나며 샘플 fidelity에서 경쟁력이 있음을 보여준다.
Denoising Diffusion GANs
1. Multimodal Denoising Distributions for Large Denoising Steps
Diffusion model 논문에서의 공통적인 가정은 $q(x_{t-1} \vert x_t)$를 가우시안 분포로 근사하는 것이다. 저자들은 이 근사가 정확한 지 질문을 던진다.
실제 denoising 분포 $q(x_{t-1} \vert x_t)$는 베이즈 정리에 의해
\[\begin{equation} q(x_{t-1} \vert x_t) \propto q(x_t \vert x_{t-1}) q(x_{t-1}) \end{equation}\]로 쓸 수 있으며, 여기서 $q(x_t \vert x_{t-1})$는 가우시안 diffusion이며 $q(x_{t-1})$은 step $t$에서의 데이터 분포이다.
실제 denoising 분포가 가우시안 형태가 되는 2가지 경우가 있다. 첫 번째 경우는 step 크기 $\beta_t$가 0에 가까운 경우로, 위 식의 곱 부분은 $q(x_t \vert x_{t-1})$가 지배적이며, diffusion process의 역은 forward process와 동일한 함수 형태로 얻을 수 있다. 따라서, $\beta_t$가 충분히 작으면 $q(x_t \vert x_{t-1})$가 가우시안이므로 denoising 분포 $q(x_{t-1} \vert x_t)$도 가우시안이며, 현재 diffusion model에서 사용되는 근사가 정확하다. 이를 만족하기 위해서 작은 $\beta_t$로 수 천 step으로 diffusion model을 구성한다.
두 번째 경우는 $q(x_t)$가 가우시안이면 denoising 분포 $q(x_{t-1} \vert x_t)$도 가우시안이 경우다. VAE 인코더로 데이터 분포 $q(x_0)$와 $q(x_t)$를 가우시안과 가깝게 하는 방법이 최근 LSGM 논문에서 연구되었다. 그러나 데이터를 가우시안으로 변환하는 것 자체가 어려우며 VAE 인코더가 이 문제를 완벽하게 해결할 수 없다. 따라서 LSGM도 복잡한 데이터셋에서는 여전히 수 십에서 수 백개의 step이 필요하다.
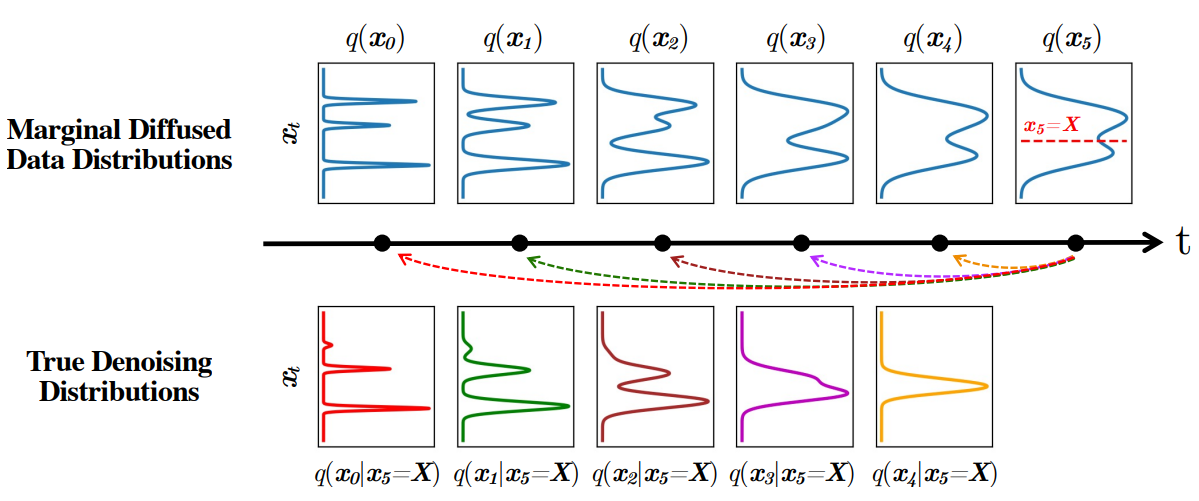
본 논문에서는 두 조건이 모두 충족되지 않는 경우, 즉 denoising step이 크고 데이터 분포가 가우시안이 아닌 경우 denoising 분포에 대한 가우시안 가정을 보장할 수 없다고 주장한다. 이를 설명하기 위해 위 그림에서 multimodal한 데이터 분포에서 다양한 denoising step 크기에 대한 실제 denoising 분포를 시각화한다. Denoising step이 커짐에 따라 실제 denoising 분포가 더 복잡해지고 다양해진다.
2. Modeling Denoising Distributions with Conitional GANs
본 논문의 목표는 denoising diffusion step $T$의 수를 줄이는 것이다. 저자들은 위의 결과에서 영감을 받아 표현적인 multimodal 분포로 denoising 분포를 모델링할 것을 제안한다. 조건부 GAN은 이미지 도메인에서 복잡한 조건부 분포를 모델링하는 것으로 나타났기 때문에 조건부 GAN을 적용하여 실제 denoising 분포 $q(x_{t-1} \vert x_t)$를 근사한다.
구체적으로, forward diffusion은 일반 diffusion model과 같으며, $T$가 작고 ($T \le 8$) $\beta_t$가 크다는 점만 다르다. Advarsarial loss를 사용하여 조건부 GAN generator $p_\theta (x_{t-1} \vert x_t)$와 $q(x_{t-1} \vert x_t)$를 일치시도록 학습된다.
\[\begin{equation} \min_\theta \sum_{t \ge 1} \mathbb{E}_{q(x_t)} [D_\textrm{adv} (q(x_{t-1} \vert x_t) \| p_\theta (x_{t-1} \vert x_t))] \end{equation}\]$D_\textrm{adv}$는 Wasserstein 거리나 JS divergence, f-divergence 등이 될 수 있다. 본 논문에서는 StyleGAN과 같은 성공적인 GAN 프레임워크들에서 널리 사용되는 non-saturating GAN을 사용한다. 이 경우 $D_\textrm{adv}$는 softened reverse KL이라 불리는 특별한 f-divergence가 되며, 이는 원래 diffusion model 학습에 사용되던 KL divergence와 다르다.
적대적 학습을 위한 시간에 의존하는 discriminator를 $D_\phi (x_{t-1}, x_t, t)$로 표기한다. Discriminator는 $N$ 차원의 $x_{t-1}$과 $x_t$를 입력으로 받아 $x_{t-1}$이 $x_t$의 그럴듯한 denoised 버전인지 결정한다. Discriminator는 다음 식으로 학습된다.
\[\begin{equation} \min_\phi \sum_{t \ge 1} \mathbb{E}_{q(x_t)} [\mathbb{E}_{q(x_{t-1} \vert x_t)}[- \log D_\phi (x_{t-1}, x_t, t)] + \mathbb{E}_{p_\theta (x_{t-1} \vert x_t)} [-\log (1-D_\phi (x_{t-1}, x_t, t))]] \end{equation}\]$p_\theta (x_{t-1} \vert x_t)$에서 뽑은 가짜 샘플이 실제 샘플 $q(x_{t-1} \vert x_t)$와 대조된다. 첫번째 기대값은 모르는 $q(x_{t-1} \vert x_t)$에서의 샘플링 필요하다. 그러나
\[\begin{equation} q(x_t, x_{t-1}) = \int dx_0 q(x_0) q(x_t, x_{t-1} \vert x_0) = \int dx_0 q(x_0) q(x_{t-1} \vert x_0) q(x_t \vert x_{t-1}) \end{equation}\]를 사용하면 첫번째 기대값을 다시 쓸 수 있다.
\[\begin{equation} \mathbb{E}_{q(x_t) q(x_{t-1} \vert x_t)} [-\log (D_\phi (x_{t-1}, x_t, t))] = \mathbb{E}_{q(x_0)q(x_{t-1} \vert x_0)q(x_t \vert x_{t-1})} [-\log(D_\phi (x_{t-1}, x_t, t))] \end{equation}\]Discriminator가 주어지면, generator를
\[\begin{equation} \max_\theta \sum_{t \ge 1} \mathbb{E}_{q(x_t)} \mathbb{E}_{p_\theta (x_{t-1} \vert x_t)} [\log (D_\phi (x_{t-1} \vert x_t, t))] \end{equation}\]로 학습시킬 수 있으며, generator를 non-saturating GAN의 목적 함수로 업데이트할 수 있다.
Parameterizing the implicit denoising model
Denoising step에서 $x_{t-1}$을 바로 예측하는 대신, diffusion model은 denoising model을
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) := q(x_{t-1} \vert x_t, x_0 = f_\theta (x_t, t))로 \end{equation}\]로 parameterize하는 것으로 해설할 수 있다. $x_0$를 denoising model $f_\theta (x_t, t)$로 예측한 다음 $x_{t-1}$을 사후 확률 분포 $q(x_{t-1} \vert x_t, x_0)$로 샘플링하는 것이다. 이 사후 확률 분포도 step 크기나 데이터 분포의 복잡성에 무관하게 항상 가우시안 분포이다.
이와 유사하게 $p_\theta(x_{t-1} \vert x_t)$를 다음과 같이 정의할 수 있다.
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) := \int p_\theta (x_0 \vert x_t) q (x_{t-1} \vert x_t, x_0) dx_0 = \int p(z) q(x_{t-1} \vert x_t, x_0 = G_\theta (x_t, z, t)) dz \end{equation}\]GAN generator $G_\theta (x_t, z, t)$는 $x_t$와 $L$차원의 잠재 변수 $z \sim p(z) := \mathcal{N}(0,I)$가 주어지면 $x_0$를 출력한다.
위와 같은 parameterization은 몇가지 장점이 있다.
- $p_\theta (x_{t-1} \vert x_t)$은 DDPM과 유사하다. 따라서 DDPM의 신경망 디자인과 같은 inductive bias를 가져올 수 있다. 주요 차이점은 DDPM의 경우 $x_0$를 $x_t$의 deterministic한 매핑으로 예측하고 본 논문의 경우 $z$에서 generator가 $x_0$를 생성한다는 것이다. 이는 본 논문의 denoising 분포가 multimodal하고 복잡할 수 있는 주요 차이점이다.
- 서로 다른 $t$에 대하여 $x_t$가 서로 다른 noise의 레벨을 가지기 때문에 1개의 신경망으로 $x_{t-1}$을 바로 예측하는 것이 어려울 수 있다. 반면 본 논문의 generator는 noise가 없는 $x_0$만 예측하고 $q(x_{t-1} \vert x_t, x_0)$로 noise를 더한다.
다음은 본 논문의 학습 파이프라인을 시각화한 것이다.
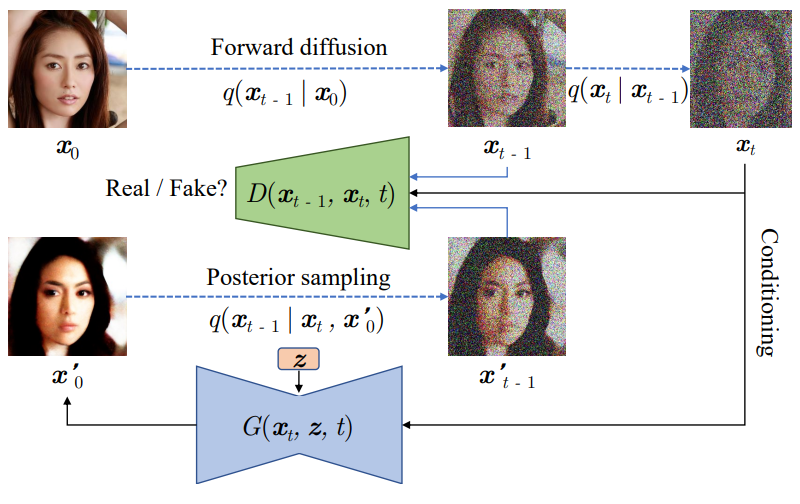
Advantage over one-shot generator
본 논문의 모델에 대한 자연스러운 질문 중 하나는 반복적으로 denoising하여 샘플을 생성하는 모델 대신 GAN을 사용하여 한 번에 샘플을 생성하도록 학습시키면 안 되는지이다. 본 논문의 모델은 전통적인 GAN에 비해 몇 가지 장점이 있다. GAN은 학습이 불안정하고 mode collapse를 겪는 것으로 알려져 있으며, 복잡한 분포에서 샘플을 one-shot으로 직접 생성하는 것이 어렵고 discriminator가 깨끗한 샘플만 볼 때 overfitting 문제가 발생한다.
반면, 본 논문의 모델은 $x_t$에 대한 강력한 컨디셔닝으로 인해 각 step이 상대적으로 모델링하기 쉬운 여러 조건부 denoising diffusion step으로 생성 프로세스를 나눈다. 또한 diffusion process는 데이터 분포를 매끄럽게 하여 discriminator가 overfitting될 가능성을 줄인다. 따라서 더 나은 학습 안정성과 모드 커버리지를 보일 것으로 기대할 수 있다.
Experiments
1. Overcoming the Generative Learning Trilemma
본 논문의 모델의 주요 장점 중 하나는 생성 학습 트릴레마의 세 가지 기준 모두에서 탁월하다는 것이다. 샘플 fidelity, 샘플 다양성, 샘플링 시간에 대한 모델의 성능을 신중하게 평가하고 CIFAR-10 데이터셋에 대한 다양한 모델과 성능을 비교한다.
그 결과는 아래 표와 같다.
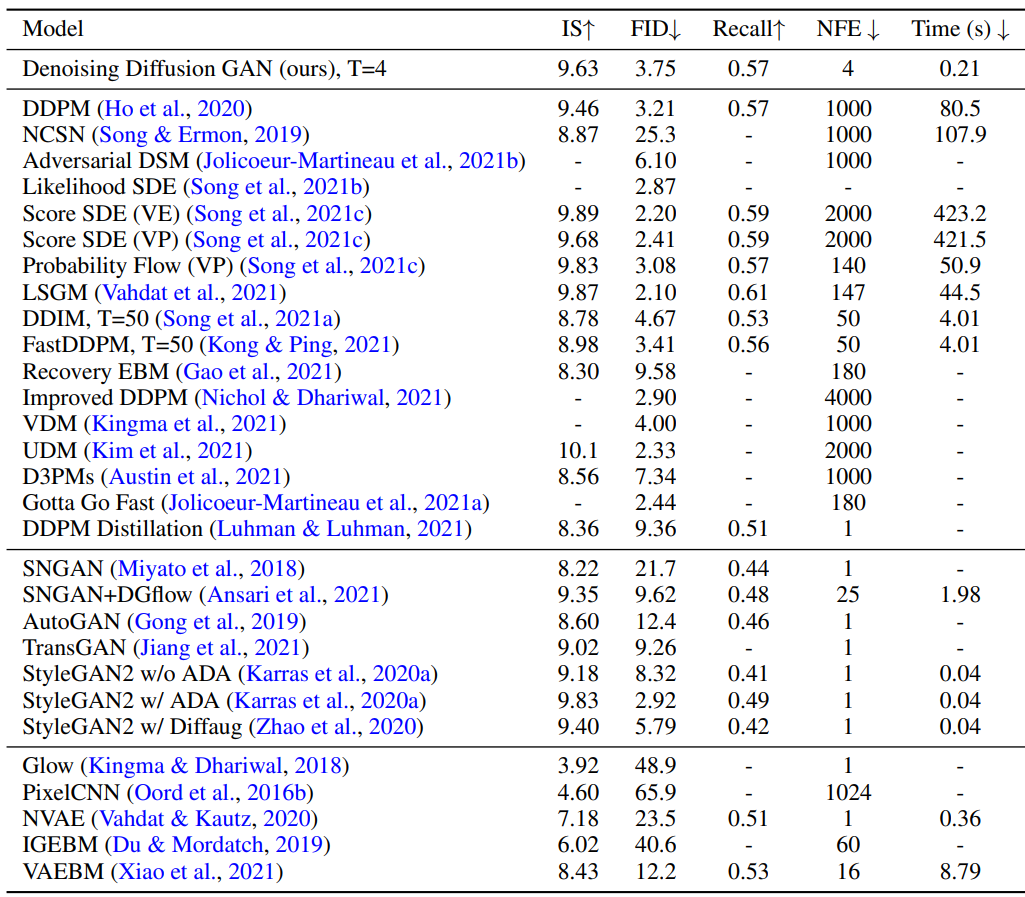
샘플 품질이 다른 diffusion model 및 GAN과 비교했을 때 경쟁력 있다는 것을 알 수 있다. 몇몇 모델들은 IS와 FID가 더 좋았지만 샘플을 생성하는 데 오래 걸린다.
다음은 다른 diffusion model들과 성능을 비교하기 위하여 FID와 샘플링 시간에 대하여 plot한 것이다.
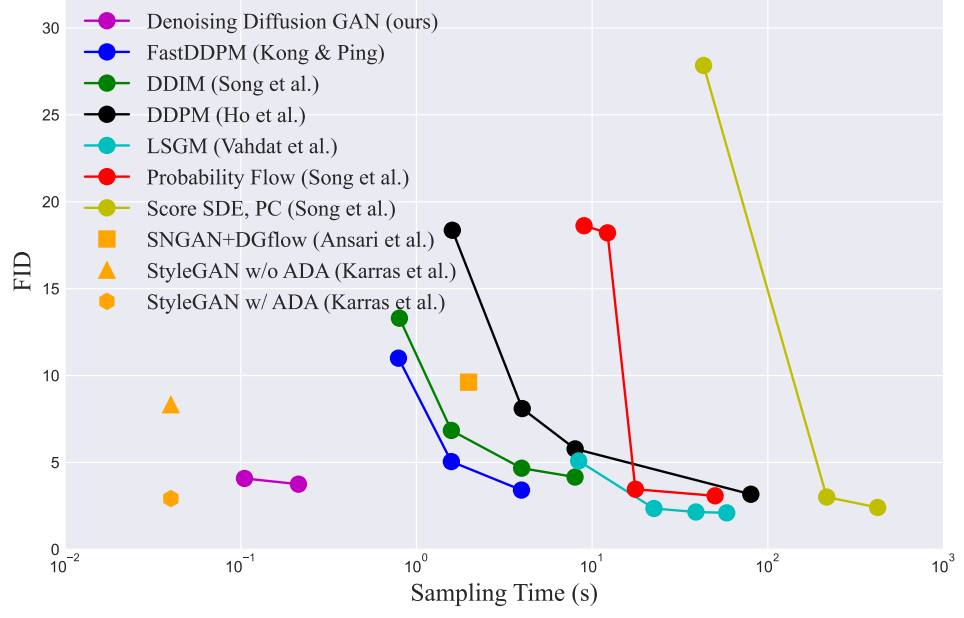
GAN과 비교하면 ADA를 적용한 StyleGAN2만 본 논문의 모델보다 샘플 품질이 더 좋다. 그러나 위 표에서 보면 recall 점수가 0.5보다 낮아 다양성에 한계가 있음을 알 수 있다. 반면, 본 논문의 모델은 상당히 더 좋은 recall 점수를 얻었으며 likelihood 기반 모델보다도 recall 점수가 좋은 경우도 있다.
다음은 CIFAR-10에서의 샘플들이다.

2. Ablation studies
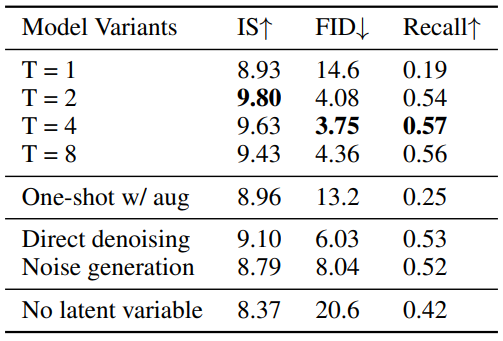
Number of denoising steps
위 표의 첫 번째 부분을 보면 다양한 denoising step 수 $T$에 대하여 ablation study를 진행한 결과를 볼 수 있다.
Diffusion as data augmentation
본 논문의 모델은 noise가 추가된 이미지를 입력으로 주기 때문에 최근 논문에서 GAN에 적용된 data augmentation과 비슷한 점이 있다. Noise가 추가된 이미지의 효과를 알아보기 위하여 저자들은 one-shot GAN을 본 논문의 신경망 구조에 forward diffusion process를 data augmentation으로 사용하여 학습시켰다. 그 결과는 위 표의 두 번째 부분에 나와 있으며, 본 논문의 모델보다 성능이 상당히 낮기 때문에 data augmentation과 동등하지 않다고 볼 수 있다.
Parameterization for $p_\theta (x_{t-1} \vert x_t)$
$x_0$의 추정된 샘플을 generator가 생성하는 대신 denoising 분포를 parameterize하는 2가지 다른 방법에 대하여 비교 실험을 하였다.
- direct denoising: 사후 확률 샘플링 없이 바로 $x_{t-1}$을 출력
- noise generation: $x_t$를 생성하는 데 추가된 noise $\epsilon_t$를 출력
2번째 방법은 deterministic하게 noise를 예측하는 대부분의 diffusion model에서 사용하는 방법이다. 실험 결과는 위 표의 세 번째 부분에 나와 있다. 2가지 방법들도 잘 작동하지만 본 논문의 parameterization의 성능이 큰 차이로 좋다.
Importance of latent variable
잠재 변수 $z$를 제거하면 denoising model이 unimodal 분포로 변환된다. 위 표의 마지막 부분을 보면 본 논문의 모델에서 $z$를 사용하지 않은 경우에 대한 실험 결과를 볼 수 있다. $z$를 사용하지 않으면 샘플 품질이 상당히 낮아지며, 이는 multimodal denoising 분포의 중요성을 보여준다.
아래 그림은 잠재 변수의 영향을 시각화하기 위해 고정된 $x_1$에 대하여 $p_\theta (x_0 \vert x_1)$로 샘플링한 샘플들을 나타낸 그림이다.

왼쪽 2개의 그림이 원본 $x_0$와 $x_0$에 noise를 추가한 $x_1$이다. 오른쪽 3개의 그림이 $p_\theta (x_0 \vert x_1)$로 샘플링한 샘플들이다. $x_1$의 대부분의 정보가 보존되면서 잠재 변수에 의해 샘플들이 다양한 것을 볼 수 있다.
3. Additional Studies
Mode Coverage
저자들은 recall 점수 외에 추가로 25-Gaussians 데이터셋과 StackedMNIST 데이터셋에서 모드 커버리지를 평가하였다. 아래 그림은 4 denoising step으로 학습한 denoising diffusion GAN의 결과를 다른 모델들과 비교한 것이다.

일반 GAN은 mode collapse가 심하게 발생하였으며, WGAN-GP는 모드 커버리지를 개선하였지만 샘플의 품질에 제한이 있다. 반면, 본 논문의 모델은 높은 샘플 품질을 유지하면서 모든 모드들을 커버하였다. DDPM의 경우 샘플 품질을 높게 유지하려면 많은 step이 필요하다는 것을 알 수 있다.
아래 표는 StackedMNIST로 모드 커버리지를 측정한 것이다.
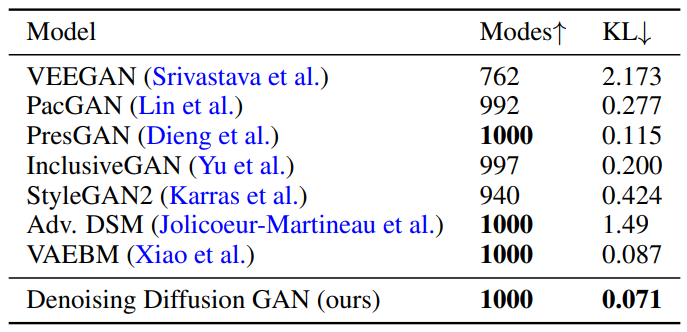
본 논문의 모델이 가장 낮은 KL을 달성하였으며, StyleGAN2과 같이 최고의 샘플 품질을 가지는 모델보다 모드 커버리지가 좋았다.
Training Stability
다음은 각각의 timestep에 대한 discriminator loss를 plot한 것이다.
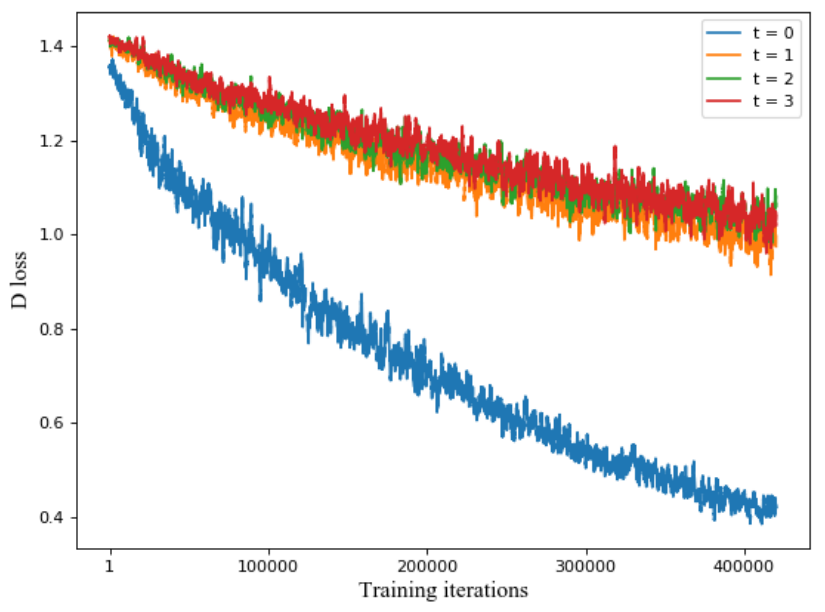
Denoising diffusion GAN의 학습이 안정적인 것을 확인할 수 있다. 이러한 안정성이 생기는 데에는 2가지 이유가 있다.
- Generator와 discriminator 모두 $x_t$로 컨디셔닝되어 강한 신호를 제공받기 때문에 둘의 균형이 유지된다.
- Diffusion process는 가짜 샘플과 실제 샘플의 분포를 서로 더 가깝게 만드는 smoothening process로 알려져 있기 때문에 상대적으로 매끄러운 분포에 대해 GAN을 학습하고 있다. 위 그래프에서 보면 $t > 0$에 대한 loss가 $t = 0$에 대한 loss보다 크다. $t > 0$은 noisy한 이미지로 학습하는 것이므로 실제 샘플과 생성된 샘플의 분포가 가깝고 이는 discriminator를 어렵게 만든다. 이러한 속성이 discriminator가 overfitting되는 것을 막아 학습 안정성을 높인다.
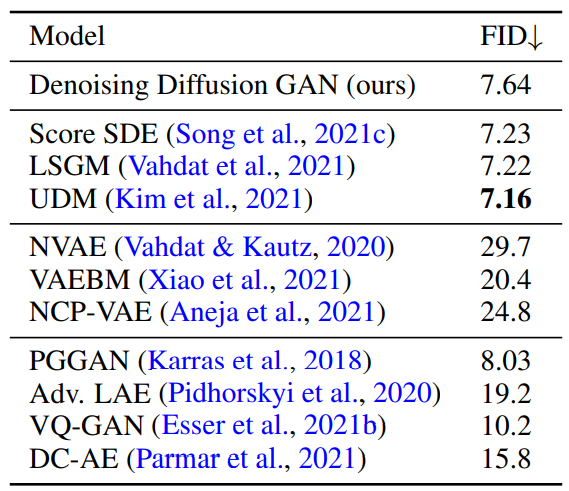
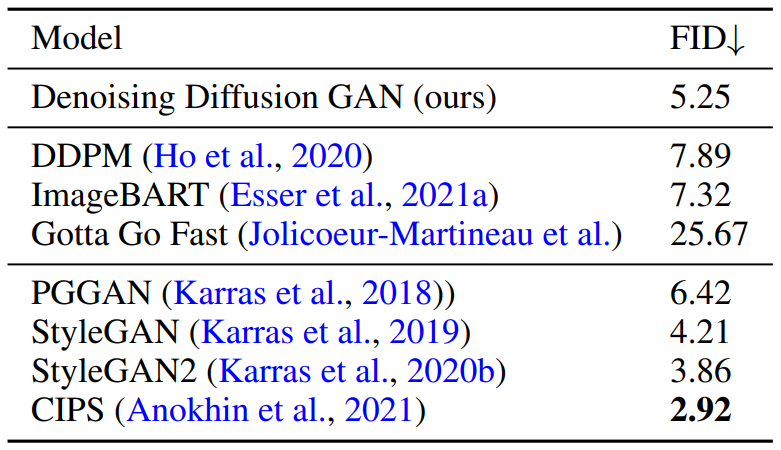
High Resolution Images
다음은 CelebA-HQ와 LSUN Church 데이터셋으로 256$\times$256에서 학습한 모델의 FID를 측정한 표와 샘플들이다.

Stroke-based image synthesis
다음은 본 논문의 모델을 stroke 기반 이미지 합성에 적용한 결과이다.

Stroke 기반 이미지 합성 모델인 SDEdit의 경우 1개의 이미지를 생성하는 데 181초가 걸리지만, 본 논문의 모델은 0.16초밖에 걸리지 않는다. 이를 통해 이미지 편집과 같은 다양한 분야에 적용할 수 있음을 알 수 있다.