[논문리뷰] Shape of Motion: 4D Reconstruction from a Single Video
ICCV 2025 (Highlight). [Paper] [Page] [Github]
Qianqian Wang, Vickie Ye, Hang Gao, Jake Austin, Zhengqi Li, Angjoo Kanazawa
UC Berkeley | Google Research
18 Jul 2024

Introduction
최근 몇 년 동안 정적인 3D 장면 모델링에서 인상적인 진전이 있었지만, 특히 하나의 동영상에서 복잡하고 동적인 3D 장면의 형상과 모션을 복구하는 것은 여전히 열린 문제로 남아 있다. 여러 동적 재구성 및 novel view synthesis (NVS) 접근법이 이 문제를 해결하려고 시도했다. 그러나 대부분의 방법은 동기화된 멀티뷰 동영상 또는 추가 LIDAR/깊이 센서에 의존한다. 최근의 monocular 접근 방식은 일반 동적 동영상에서 작동할 수 있지만 일반적으로 짧은 거리의 scene flow 또는 deformation field로 3D 장면 모션을 모델링하므로 동영상에 지속되는 3D 모션 궤적을 캡처하지 못한다.
일반적인 동영상에 대한 오랜 과제는 재구성 문제의 제약이 부족하다는 것이다. 저자들은 두 가지 주요 통찰력을 통해 이 문제를 해결하였다. 첫 번째는 이미지 공간에서의 역학은 복잡하고 불연속적일 수 있지만 3D 모션은 연속적인 단순 rigid motion의 합이라는 것이다. 두 번째는 데이터 기반 prior가 3D 장면 형상과 모션에 글로벌하게 일관된 표현으로 잘 통합되는 보완적인 단서라는 것이다.
저자들은 이 두 가지 통찰력에 기반으로 동적 장면을 지속적인 3D Gaussian 세트로 표현하고 공유된 \(\mathbb{SE}(3)\) motion base들로 동영상 전체의 모션을 표현하였다. 연속되는 프레임 간의 3D correspondence를 계산하는 기존 scene flow와 달리 본 논문의 표현은 전체 동영상에 대한 지속적인 3D 궤적을 복구하여 지속적인 3D tracking을 가능하게 한다. 생성된 3D 궤적은 3D 공간과 시간을 통해 각 포인트의 움직임을 추적하는 기하학적 패턴을 캡처하므로 본 논문의 방법을 Shape of Motion이라 부른다.
Method
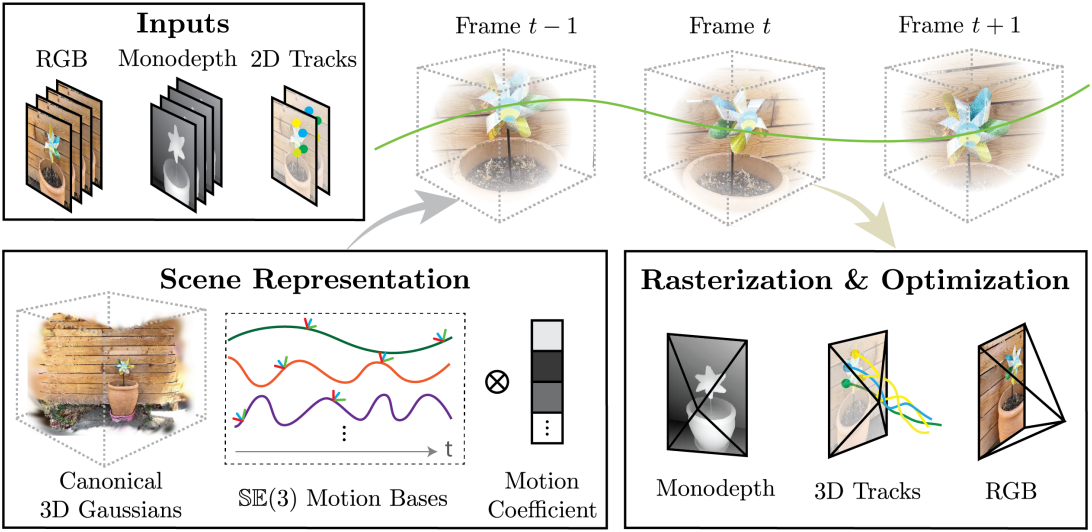
- 목표: 전체 동적 장면의 형상과 장면의 모든 포인트의 전체 길이 3D 모션 궤적을 복구
- 입력
- $T$개의 동영상 프레임 \(\{I_t \in \mathbb{R}^{H \times W \times 3}\}\)
- 카메라 intrinsics \(\mathbf{K}_t \in \mathbb{R}^{3 \times 3}\)
- world-to-camera extrinsics \(\textbf{E}_t \in \mathbb{SE}(3)\)
동영상에서 동적인 3D Gaussian을 최적화하는 것은 매우 어렵다. 각 시점에서 장면의 움직이는 피사체는 하나의 시점에서만 해당 포즈로 관찰된다. 이러한 모호함을 극복하기 위해 저자들은 두 가지 통찰력을 얻었다.
- Projection된 2D 역학은 동영상에서 복잡할 수 있지만 장면의 3D 모션은 저차원이며 더 간단한 rigid motion들의 합으로 구성된다.
- 강력한 데이터 기반 prior, 즉 monocular depth 추정과 장거리 2D tracking은 3D 장면에 대한 보완적이지만 잡음이 많은 신호를 제공한다.
저자들은 이러한 잡음이 많은 추정치를 장면 형상과 모션 모두에 대해 전체적으로 일관된 표현으로 융합할 수 있는 시스템을 제안하였다.
- Notation
- \(\mathbf{g}_0 = (\boldsymbol{\mu}_0, \mathbf{R}_0, \mathbf{s}, o, \mathbf{c})\): 표준 프레임 $t_0$에서의 3D Gaussian
- \(\boldsymbol{\mu}_0 \in \mathbb{R}^3\): $t_0$에서의 3D mean
- \(\mathbf{R}_0 \in \mathbb{SO}(3)\): $t_0$에서의 orientation
- $\mathbf{s} \in \mathbb{R}^3$, $o \in \mathbb{R}$, $\mathbf{c} \in \mathbb{R}^3$: scale, opacity, color
1. Dynamic Scene Representation
Scene Motion Parameterization
동적인 3D 장면을 모델링하기 위해 $N$개의 3D Gaussian을 추적하고 프레임당 rigid transformation을 통해 시간이 지남에 따라 위치와 방향을 변경한다. 시간 $t$에서 움직이는 3D Gaussian의 경우, 포즈 파라미터 \((\boldsymbol{\mu}_t, \mathbf{R}_t)\)는
\[\begin{equation} \mathbf{T}_{0 \rightarrow t} = [\mathbf{R}_{0 \rightarrow t} \; \mathbf{t}_{0 \rightarrow t}] \in \mathbb{SE}(3) \end{equation}\]을 통해 표준 프레임 $t_0$에서 $t$로 변환된다.
\[\begin{equation} \boldsymbol{\mu}_t = \mathbf{R}_{0 \rightarrow t} \boldsymbol{\mu}_0 + \mathbf{t}_{0 \rightarrow t}, \quad \mathbf{R}_t = \mathbf{R}_{0 \rightarrow t} \mathbf{R}_0 \end{equation}\]각 Gaussian에 대해 독립적으로 3D 모션 궤적을 모델링하는 대신 모든 Gaussian에서 공유되는 $B \ll N$개의 학습 가능한 basis 궤적의 세트 \(\{\mathbf{T}_{0 \rightarrow t}^{(b)}\}_{b=1}^B\)를 정의한다. 그런 다음 각 시간 $t$에서의 transformation \(\mathbf{T}_{0 \rightarrow t}\)는 다음과 같이 포인트별 basis 계수 \(\mathbf{w}^{(b)}\)를 통해 basis 궤적 세트의 가중합으로 계산된다.
\[\begin{equation} \mathbf{T}_{0 \rightarrow t} = \sum_{b=0}^B \mathbf{w}^{(b)} \mathbf{T}_{0 \rightarrow t}^{(b)}, \quad \textrm{where} \; \| \mathbf{w}^{(b)} \| = 1 \end{equation}\]\(\mathbf{T}_{0 \rightarrow t}^{(b)}\)를 6D rotation 및 translation으로 parameterize한다. 최적화 과정에서 global motion base와 각 3D Gaussian의 모션 계수들을 공동으로 학습시킨다. 이러한 motion base는 궤적을 저차원으로 명시적으로 정규화하여 서로 유사하게 움직이는 3D Gaussian이 유사한 모션 계수로 표시되도록 장려한다.
Rasterizing 3D trajectories
3D Gaussian의 모션 궤적을 쿼리 프레임 $I_t$로 rasterize한다. 즉, intrinsics \(\textbf{K}_t\)와 extrinsics \(\textbf{E}_t\)가 있는 시간 $t$의 쿼리 카메라에 대해 rasterization을 수행하여 목표 시간 $t^\prime$에서 각 픽셀에 해당하는 표면 점의 예상 3D world 좌표를 포함하는 맵 \({}^{\textbf{w}} \hat{\textbf{X}}_{t \rightarrow t^\prime} \in \mathbb{R}^{H \times W \times 3}\)을 얻는다.
\[\begin{equation} {}^{\textbf{w}} \hat{\textbf{X}}_{t \rightarrow t^\prime} (\textbf{p}) = \sum_{i \in H(\textbf{p})} T_i \alpha_i \boldsymbol{\mu}_{i, t^\prime} \end{equation}\]여기서 $H(\textbf{p})$는 쿼리 시간 $t$에서 픽셀 $p$와 교차하는 Gaussian 집합이다. 주어진 픽셀 $p$에 대한 시간 $t^\prime$에서의 2D 대응 위치인 \(\hat{\textbf{U}}_{t \rightarrow t^\prime} (\textbf{p})\)와 해당 깊이 값 \(\hat{\textbf{D}}_{t \rightarrow t^\prime} (\textbf{p})\)은 다음과 같다.
\[\begin{equation} \hat{\textbf{U}}_{t \rightarrow t^\prime} (\textbf{p}) = \Pi (\textbf{K}_{t^\prime} {}^{\textbf{c}} \hat{\textbf{X}}_{t \rightarrow t^\prime} (\textbf{p})), \quad \hat{\textbf{D}}_{t \rightarrow t^\prime} (\textbf{p}) = ({}^{\textbf{c}} \hat{\textbf{X}}_{t \rightarrow t^\prime} (\textbf{p}))_{[3]} \\ \textrm{where} \quad {}^{\textbf{c}} \hat{\textbf{X}}_{t \rightarrow t^\prime} (\textbf{p}) = \textbf{E}_{t^\prime} {}^{\textbf{w}} \hat{\textbf{X}}_{t \rightarrow t^\prime} (\textbf{p}) \end{equation}\]여기서 $\Pi$는 perspective projection 연산이고, $(\cdot)_{[3]}$은 벡터의 세 번째 element이다.
2. Optimization
먼저 기존 방법들을 사용하여 다음 추정치들을 준비한다.
- \(\{\textbf{M}_t\}\): Track-Anything을 사용하여 얻을 수 있는 각 프레임에 대한 움직이는 물체 마스크
- \(\{\textbf{D}_t\}\): Depth Anything을 사용하여 계산된 각 프레임에 대한 monocular depth map
- \(\{\textbf{U}_{t \rightarrow t^\prime}\}\): TAPIR을 사용하여 얻을 수 있는 전경 픽셀에 대한 long-range 2D track
Relative depth map이 더 세밀한 디테일을 포함하는 경향이 있기 때문에 프레임별로 글로벌 scale과 shift를 계산하여 relative depth map을 metric depth map과 정렬하고 이를 최적화에 사용한다. 정렬된 depth map을 사용하여 unprojection된 2D track을 움직이는 물체에 대한 잡음이 있는 초기 3D track \(\{\textbf{X}_t\}\)로 처리한다.
장면의 정적 부분의 경우 표준 정적 3D Gaussian을 사용하여 모델링하고 정렬된 depth map을 사용하여 3D 공간으로 unprojection하여 3D 위치를 초기화한다. 정적 및 동적 Gaussian은 공동으로 최적화되고 함께 rasterize되어 이미지를 형성한다. 아래에서는 동적 Gaussian의 최적화 프로세스를 설명하는 데 중점을 둔다.
Initialization
먼저, 가장 많은 3D track이 있는 프레임을 표준 프레임 $t_0$로 선택한다. 이 초기 관측에서 무작위로 샘플링된 $N$개의 3D track 위치로 표준 프레임의 Gaussian 평균 \(\boldsymbol{\mu}_0\)를 초기화한다.
그런 다음 잡음이 있는 3D track \(\{\textbf{X}_t\}\)의 속도에 대해 k-means clustering을 수행하고 이러한 $B$개의 track 클러스터에서 motion base \(\{\textbf{T}_{0 \rightarrow t}^{(b)}\}_{b=1}^B\)을 초기화한다. 모든 $t\tau = 0, \ldots, T$에 대해 클러스터 $b$에 속하는 궤적 세트 \(\{\textbf{X}_0\}_b\)와 \(\{\textbf{X}_\tau\}_b\) 사이의 weighted Procrustes alignment을 사용하여 basis transform \(\textbf{T}_{0 \rightarrow \tau}^{(b)}\)를 초기화한다. 여기서 가중치는 TAPIR 예측의 uncertainty 및 visibility score를 사용하여 계산된다.
표준 프레임의 클러스터 $b$ 중심으로부터의 거리에 따라 지수적으로 감소하도록 각 Gaussian의 \(\textbf{w}^{(b)}\)를 초기화한다. 그런 다음 \(\boldsymbol{\mu}_0\), \(\textbf{w}^{(b)}\), \(\{\textbf{T}_{0 \rightarrow t}^{(b)}\}_{b=1}^B\)을 최적화하여 temporal smoothness 제약 조건 하에서 L1 loss로 관찰된 3D track들을 fitting한다.
Training
두 가지 loss 세트로 동적 Gaussian을 학습시킨다. 첫 번째 loss 세트는 프레임별 색상, 깊이, 마스크 입력에 대한 재구성 loss로 구성된다. 구체적으로, 각 학습 step에서 학습 카메라 \((\textbf{K}_t, \textbf{E}_t)\)로부터 이미지 \(\hat{\textbf{I}}_t\), 깊이 \(\hat{\textbf{D}}_t\) 및 마스크 \(\hat{\textbf{M}}_t\)를 렌더링한다. 프레임별로 독립적으로 적용된 재구성 loss를 사용하여 렌더링된 값들을 supervise한다.
\[\begin{equation} L_\textrm{recon} = \| \hat{\mathbf{I}} - \mathbf{I} \|_1 + \lambda_\textrm{depth} \| \hat{\mathbf{D}} - \mathbf{D} \|_1 + \lambda_\textrm{mask} \| \hat{\mathbf{M}} - 1 \|_1 \end{equation}\]두 번째 loss 세트는 프레임 간 Gaussian의 모션을 학습시킨다. 구체적으로, 무작위로 샘플링된 쿼리 시간 $t$와 목표 시간 $t^\prime$ 쌍에 대해 2D track \(\hat{\textbf{U}}_{t \rightarrow t^\prime}\)와 reprojection된 깊이 \(\hat{\textbf{D}}_{t \rightarrow t^\prime}\)를 추가로 렌더링한다. 그런 다음 long-range 2D track 추정치로 이러한 렌더링된 correspondence들을 학습시킨다.
\[\begin{aligned} L_\textrm{track-2d} &= \| \mathbf{U}_{t \rightarrow t^\prime} - \hat{\mathbf{U}}_{t \rightarrow t^\prime} \|_1 \\ L_\textrm{track-depth} &= \| \hat{\mathbf{D}}_{t \rightarrow t^\prime} - \hat{\mathbf{D}} (\mathbf{U}_{t \rightarrow t^\prime}) \|_1 \end{aligned}\]마지막으로 무작위로 샘플링된 동적 Gaussian과 k-nearest neighbor들 간의 거리 보존 loss를 적용한다.
\[\begin{equation} L_\textrm{rigidity} = \| \textrm{dist} (\hat{\mathbf{X}}_t, \mathcal{C}_k (\hat{\mathbf{X}}_t)) - \textrm{dist} (\hat{\mathbf{X}}_{t^\prime}, \mathcal{C}_k (\hat{\mathbf{X}}_{t^\prime})) \|_2^2 \end{equation}\]\(\hat{\textbf{X}}_t\)와 \(\hat{\textbf{X}}_{t^\prime}\)은 시간 $t$ 및 $t^\prime$에서 Gaussian의 위치를 나타내고 \(\mathcal{C}_k(\hat{\textbf{X}}_t)\)는 \(\hat{\textbf{X}}_t\)의 k-nearest neighbor들을 나타낸다. $\textrm{dist}(\cdot,\cdot)$는 Euclidean distance이다.
Experiments
- 구현 디테일
- UniDepth로 intrinsic과 metric depth map을 계산
- Droid-SLAM을 RGB-D 모드로 실행하여 카메라 포즈를 계산
- optimizer: Adam
- iteration
- 초기 fitting: 1,000 iteration
- 공동 최적화: 500 epochs
- $B$ = 20
- 초기 Gaussian 수
- 정적 Gaussian: 10만 개
- 동적 Gaussian: 4만 개
- 프레임 수: 300
- 해상도: 960$\times$720
- 학습은 A100 GPU 1개에서 2시간 소요
- 렌더링 FPS: 40
1. Evaluation on iPhone Dataset
다음은 iPhone 데이터셋에서 3D tracking 결과를 비교한 것이다.
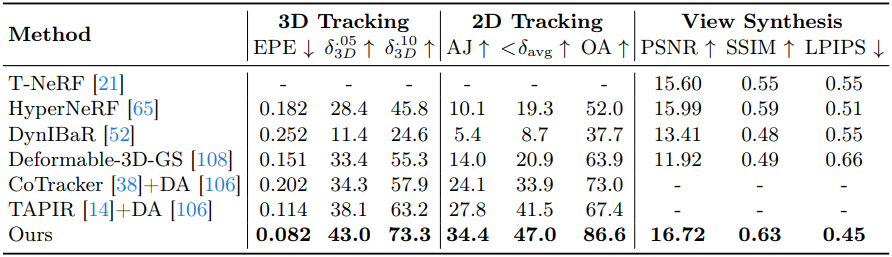
다음은 iPhone 데이터셋에서 NVS를 비교한 것이다.

다음은 PCA 이후의 모션 계수와 depth map 예측의 예시들이다.

2. Evaluation on the Kubric dataset
다음은 Kubric 데이터셋에서 3D tracking을 평가한 표이다.

다음은 최적화된 모션 계수의 처음 3개 PCA 성분을 시각화한 것이다.

3. Ablation studies
다음은 iPhone 데이터셋에서의 ablation 결과이다.

Limitations
- 대부분의 이전 monocular 동적 NVS 방법과 유사하게 여전히 장면별 test-time 최적화가 필요하다.
- 카메라 시점의 큰 변화를 처리할 수 없다.
- 기존 알고리즘에서 얻은 정확한 카메라 파라미터에 의존하여 텍스처가 없는 영역이나 움직이는 물체가 지배하는 장면에서 잠재적인 오차가 발생한다.
- 움직이는 물의 마스크를 생성하기 위해 사용자 입력에 의존한다.