[논문리뷰] Regularized Vector Quantization for Tokenized Image Synthesis (Reg-VQ)

arXiv 2023. [Paper]
Jiahui Zhang, Fangneng Zhan, Christian Theobalt, Shijian Lu
Nanyang Technological University | Max Planck Institute for Informatics
11 Mar 2023

Introduction

Multi-modal 이미지 합성과 Transformer의 보급으로 인해 데이터 modality에 관계없이 데이터 모델링을 통합하는 것이 연구 커뮤니티의 관심을 끌었다. 서로 다른 데이터 modality에 걸쳐 일반적인 데이터 표현을 목표로 하는 discrete representation learning은 통합 모델링에서 중요한 역할을 한다. 특히, vector quantization model(ex. VQ-VAE, VQ-GAN)은 이미지를 개별 토큰으로 이산화하여 일반적인 이미지 표현을 학습하기 위한 유망한 모델로 부상하고 있다. 토큰화된 표현을 사용하면 autoregressive model과 diffusion model과 같은 생성 모델을 적용하여 이미지 생성을 위한 순차적 토큰의 종속성을 수용할 수 있으며, 이를 이 컨텍스트에서 tokenized image synthesis라고 한다.

Vector quantization model은 이산적인 토큰의 선택에 따라 deterministic quantization과 stochastic quantization으로 크게 분류할 수 있다. 특히 VQ-GAN과 같은 일반적인 deterministic 방법은 Argmin이나 Argmax를 통해 가장 일치하는 토큰을 직접 선택하는 반면 Gumbel-VQ와 같은 stochastic 방법은 예측된 토큰 분포에서 확률적으로 샘플링하여 토큰을 선택한다. 반면에 deterministic quantization은 codebook embedding의 많은 부분이 0에 가까운 값으로 유효하지 않은 codebook collapse라는 잘 알려진 어려움을 겪는다.

또한 deterministic quantization은 토큰이 가장 일치하는 토큰을 선택하는 대신 일반적으로 랜덤하게 샘플링되는 생성 모델링의 inference 단계와 일치하지 않는다. 대신 stochastic quantization은 Gumbel-Softmax를 사용하여 예측된 토큰 분포에 따라 토큰을 샘플링하여 codebook collapse를 방지하고 inference 불일치를 완화한다. 그러나 stochastic quantization에서는 대부분의 codebook embedding이 유효한 값임에도 불구하고 vector quantization에 실제로 활용되는 부분은 극히 일부에 불과하여 codebook 활용도가 낮다. 게다가 stochastic 방법은 분포에서 랜덤하게 토큰을 샘플링하기 때문에 샘플링된 토큰에서 재구성된 이미지는 일반적으로 원본 이미지와 잘 일치하지 않아 섭동된 재구성 목적 함수와 신뢰할 수 없는 이미지 재구성으로 이어진다.

본 연구에서는 두 가지 관점에서 정규화를 통해 위의 문제를 효과적으로 방지할 수 있는 regularized quantization 프레임워크를 도입한다. 특히, 소수의 codebook embedding만 유효하거나 quantization에 사용되는 codebook collapse와 낮은 codebook 활용을 피하기 위해 균등 분포를 토큰 분포의 prior로 가정하여 prior distribution regularization을 도입한다. Posterior 토큰 분포는 quantization 결과에 의해 근사화될 수 있으므로 prior 토큰 분포와 posterior 토큰 분포 간의 불일치를 측정할 수 있다. 학습 중 불일치를 최소화함으로써 quantization 프로세스는 모든 codebook embedding을 사용하도록 정규화되어 예측된 토큰 분포가 소수의 codebook embedding으로 collapse되는 것을 방지한다.

Deterministic quantization은 inference 단계 불일치로 인해 어려움을 겪고 stochastic quantization은 섭동된 재구성 목적 함수로 인해 어려움을 겪기 때문에 stochastic mask regularization를 도입하여 이들 사이의 균형을 잘 맞춘다. 구체적으로, stochastic mask regularization는 stochastic quantization을 위해 특정 비율의 영역을 임의로 마스킹하고 deterministic quantization을 위해 마스킹되지 않은 영역을 남겨둔다. 이는 토큰 선택과 quantization 결과에 대한 불확실성을 도입하여 토큰이 랜덤하게 선택되는 생성 모델링의 inference 단계와의 격차를 좁한다. 또한 최적의 이미지 재구성 및 생성을 위한 마스킹 비율 선택을 분석하기 위해 철저하고 포괄적인 실험을 수행한다.

반면에 랜덤하게 샘플링된 토큰을 사용하면 stochastic하게 quantize된 영역이 섭동된 재구성 목적 함수로 인해 어려움을 겪을 것이다. 섭동된 재구성 목적 함수는 주로 랜덤하게 샘플링된 토큰에서 원본 이미지의 완벽한 재구성을 위한 target에서 발생한다. L1 loss로 완벽한 이미지 재구성을 naive하게 시행하는 대신 탄력있는 이미지 재구성을 위한 contrastive loss를 도입하여 섭동된 재구성 목적 함수를 크게 완화한다. PatchNCE와 유사하게 contrastive loss는 동일한 공간적 위치에 있는 patch를 positive pair로 취급하고 다른 것들은 negative pair로 취급한다. Positive pair을 더 가깝게 밀고 negative pair을 멀리 당기면 탄력적인 이미지 재구성이 가능하다.

랜덤하게 샘플링된 토큰의 또 다른 문제는 재구성 목적 함수에서 서로 다른 스케일의 섭동(perturbation)을 도입하는 경향이 있다는 것이다. 따라서 샘플링된 토큰 임베딩과 가장 일치하는 토큰 임베딩 간의 불일치에 따라 서로 다른 영역의 당기는 힘을 조정하는 Probabilistic Contrastive Loss (PCL)을 도입한다.

Method

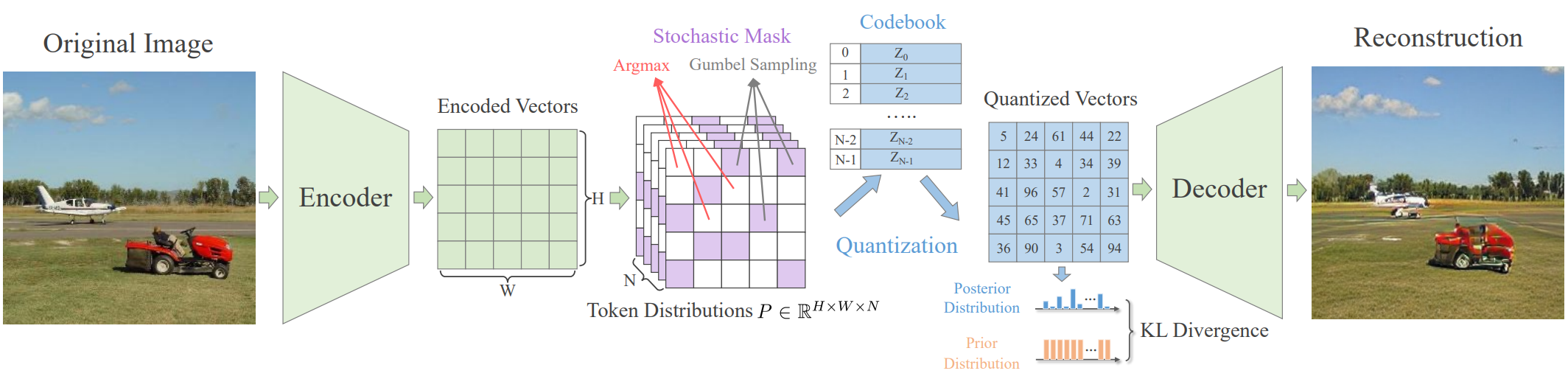
위 그림에서 볼 수 있듯이 regularized quantization 프레임워크는 deterministic quantization과 stochastic quantization을 결합하며 인코더 $E$, 디코더 $G$, codebook \(\mathcal{Z} = \{z_n\}_{n=1}^N \in \mathbb{R}^{N \times d}\)로 구성된다. 여기서 $N$은 codebook의 크기이고 $d$는 임베딩의 차원이다. 입력 이미지 $X$가 주어지면 인코더는 토큰 분포 $x_i \in \mathbb{R}^N, i \in [1, H \times W]$의 공간적 컬렉션을 생성하는 데 사용된다. 여기서 $H \times W$는 공간 벡터의 크기이다. 그런 다음 각 인코딩된 벡터는 토큰화된 표현 (즉, codebook embedding의 인덱스)을 생성하는 예측된 토큰 분포에 따라 개별 토큰으로 매핑된다. 인덱스와 관련된 codebook embedding은 최종적으로 디코더에 입력되어 입력 이미지를 재구성한다.

학습된 vector quantization 프레임워크를 사용하면 codebook 인덱스(즉, 토큰)로 이미지를 표현할 수 있다. 이미지의 개별 토큰을 사용하여 autoregressive model과 diffusion model과 같은 생성 모델을 적용하여 토큰 간의 종속성을 구축할 수 있다. 생성 모델링의 inference 단계에서 이미지 합성을 위해 일련의 토큰을 샘플링할 수 있다. 토큰 시퀀스를 해당 codebook embedding에 다시 매핑하면 임베딩을 디코더에 공급하여 이미지를 쉽게 생성할 수 있다.

1. Prior Distribution Regularization

널리 사용되는 vector quantization model은 일반적으로 codebook collapse나 codebook 활용도가 낮아서 소수의 codebook embedding만 quantization에 사용되는 문제가 심각하다. 따라서 저자들은 vector quantization 프로세스를 정규화하기 위해 prior distribution regularization를 제안한다. 특히 quantization에 사용되는 토큰에 대한 사전 분포(prior)를 가정한다. 이상적으로는 사전 분포는

\[\begin{equation} P_{prior} = \bigg[ \frac{1}{N}, \cdots, \frac{1}{N} \bigg] \in \mathbb{R}^N \end{equation}\]

으로 표시되는 균일한 이산 분포일 것으로 기대되며, 이는 모든 code embedding이 균일하게 사용될 수 있고 해당 정보 용량이 최대 엔트로피 원칙에 따라 최대화될 수 있음을 의미한다. Quantization 과정에서 $H \times W$ 크기의 이미지 feature가 해당 토큰에 매핑되므로 각 feature의 예측된 quantization 결과는 one-hot vector $p_i, i \in [1, HW]$로 나타낼 수 있다. 따라서 posterior 토큰 분포 $P_{post}$는

\[\begin{equation} P_{post} = \sum_{i=1}^{H \times W} \frac{p_i}{H \times W} = [p_1, p_2, \cdots, p_N] \end{equation}\]

와 같이 모든 one-hot vector의 평균으로 근사할 수 있다. 그러면 prior 토큰 분포와 예상 토큰 분포 간의 불일치는 다음과 같이 KL-divergence로 측정할 수 있다.

\[\begin{equation} \mathcal{L}_{kl} = KL (P_{post}, P_{prior}) = - \sum_n^N p_n \log \frac{1 / N}{p_n} \end{equation}\]

KL-divergence $\mathcal{L}_{kl}$을 최소화함으로써 vector quantization을 효과적으로 정규화하여 codebook collapse와 낮은 codebook 활용을 방지할 수 있다.

2. Stochastic Mask Regularization

반면에 가장 가능성이 높은 토큰을 선택하는 deterministic quantization은 토큰이 예측된 분포에 따라 랜덤하게 샘플링되는 생성적 모델링의 inference 단계와의 불일치로 이어질 것이다. 대신 stochastic quantization을 사용하면 quantization 중에 stochasticity를 도입하여 inference 단계와의 불일치을 완화하는 데 도움이 된다. 그럼에도 불구하고, stochastic quantization은 샘플링된 토큰이 원본 이미지와 일치하지 않을 수 있으므로 재구성 목적 함수를 섭동시키는 경향이 있다. 결과적으로, stochastic quantization의 생성 품질(FID)은 아래 그래프와 같이 deterministic quantization에 비해 작은 개선을 보인다.

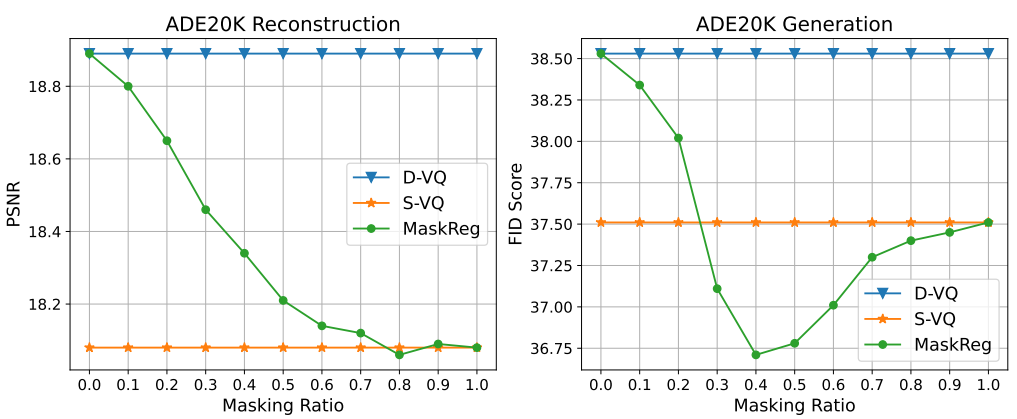
섭동되지 않은 재구성 목적 함수와 inference 단계 불일치 사이의 균형을 잘 맞추기 위해 stochastic quantization과 deterministic quantization을 위한 이미지 영역을 조정한다. 이미지 영역 조정을 위해 확률적 마스크를 적용하여 deterministic quantization과 stochastic quantization을 결합하는 stochastic mask regularization을 설계한다.

구체적으로, 모든 인코딩된 벡터에 대해 예측된 토큰 확률 $P \in \mathbb{R}^{H \times W \times N}$을 사용하여 마스크 $M \in \mathbb{R}^{H \times W}$을 Gumbel-softmax로 랜덤하게 설정한다. 마스크에서 토큰 샘플링을 위한 영역은 ‘1’로, Argmax와 가장 일치하는 토큰을 선택하기 위한 영역은 ‘0’으로 나타낸다. Argmax 및 Gumbel 샘플링을 통해 quantize된 벡터를 각각 $X_{argmax}$와 $X_{gumbel} \in \mathbb{R}^{H \times W \times N}$으로 나타내면 재구성 목적 함수는 다음과 같이 공식화될 수 있다.

\[\begin{equation} \mathcal{L}_{rec} = \| X - G(X_{argmax} \ast (1-M) + X_{gumbel} \ast M) \|_1 \end{equation}\]

여기서 $G$는 디코더이다.

위 그림에서와 같이 다양한 마스킹 비율에 따른 효과를 분석하기 위해 포괄적인 실험을 수행했으며 40%의 마스킹 비율이 최상의 이미지 재구성 및 생성 품질(최상의 FID)을 산출하는 것으로 입증되었다. Argmax와 Gumbel 샘플링 연산은 모두 미분할 수 없으므로 기울기 역전파에서 Argmax 연산을 Softmax로, Gumbel 연산을 Gumbel-Softmax로 대체하여 reparameterization trick을 적용한다. 제안된 regularized quantization의 forward 및 backward propagation의 pseudo code는 Algorithm 1과 같다.

3. Probabilistic Contrastive Loss

Stochastic mask regularization는 inference 단계와의 불일치를 완화한다. 그러나 stochastic quantization을 사용하는 이미지 영역의 경우 모델 학습은 여전히 랜덤하게 샘플링된 토큰으로 인해 재구성 목적 함수가 섭동되는 문제가 있다. 따라서 저자들은 stochastic quantization 영역에서 섭동된 목적 함수를 완화하기 위해 probabilistic contrastive loss (PCL)을 제안한다. L1 loss가 있는 원본 이미지의 완벽한 재구성을 위한 대상의 섭동된 목적 함수로서 제안된 PCL은 contrastive learning을 통해 stochastic quantization 영역에서 탄력적인 이미지 재구성이 가능하다.

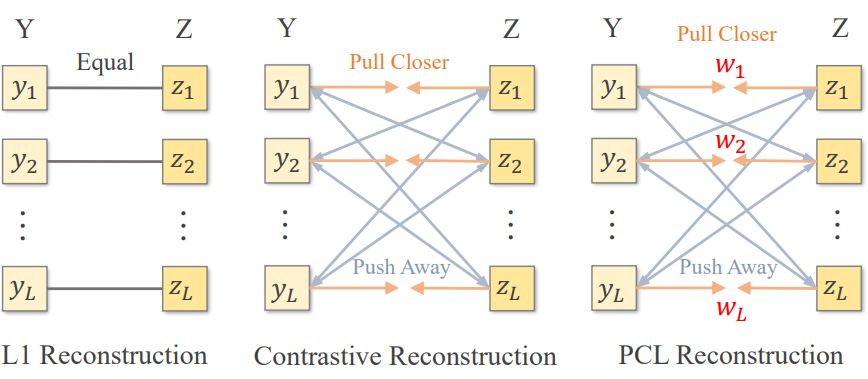
완벽한 이미지 재구성을 강요하는 대신, contrastive learning은 위 그림과 같이 선택된 positive pair을 더 가깝게 당기고 negative pair을 밀어냄으로써 해당 이미지 간의 상호 의존 정보(mutual information)를 최대화하는 것을 목표로 한다. 원본 이미지와 재구성된 이미지의 공간적 위치는 PCL에서 positive pair로 간주되고 나머지는 negative pair로 간주된다. 따라서 이미지 재구성을 위한 vanilla contrastive loss \(\mathcal{L}_{cl}\)은 다음과 같이 공식화될 수 있다.

\[\begin{equation} \mathcal{L}_{cl} = - \frac{1}{L} \sum_{i=1}^L \log \frac{e^{y_i \cdot z_i / \tau}}{e^{y_i \cdot z_i / \tau} + \sum_{j \ne i} e^{y_i \cdot z_j / \tau}} \end{equation}\]

여기서 $Y = [y_1, \cdots, y_L]$과 $Z = [z_1, \cdots, z_L]$은 각각 원본 이미지와 재구성 이미지에서 추출된 feature patch들이다. $\tau$는 temperature parameter이고 $L$은 이미지 feature의 수이다.

Perceptual loss는 이미지 재구성을 위해 좋은 지각 품질을 유지하는 데 도움이 된다. 따라서 사전 학습된 VGG-19 네트워크를 사용하여 원본 이미지와 재구성된 이미지에서 multi-layer 이미지 feature (relu1_2, relu2_2, relu3_3, relu4_3, relu5_3)을 추출하여 contrastive learning pair을 구성한다. Contrastive loss는 학습 중 perceptual loss와 함께 사용된다.

Probabilistic Contrast

Gumbel 샘플링의 stochasticity로 인해 샘플링된 토큰은 Argmax에서 선택한 가장 일치하는 토큰과 다양한 불일치를 나타내는 경향이 있다. 직관적으로 가장 잘 일치하는 것과 더 큰 불일치가 있는 샘플링된 토큰은 더 심각한 객관적 섭동을 생성한다. 따라서 원본 이미지와 재구성된 이미지 사이의 당기는 힘은 최적의 contrastive learning을 위해 섭동 크기에 따라 적응되어야 한다.

토큰 샘플링 결과(즉, 섭동 크기)에 따라 서로 다른 feature의 당기는 힘을 조정하기 위해 weighting parameters \(\{w_i\}_{i=1}^L\)을 사용하는 Probabilistic Contrastive Loss (PCL)을 도입한다. $w_i$는 랜덤하게 샘플링된 임베딩 $z_s$와 가장 일치하는 임베딩 $z_q$ 사이의 유클리드 거리를 계산하여 생성된다.

\[\begin{equation} w_i = \| z_s - z_q \|_2^2 \end{equation}\]

그러면 probabilistic contrastive loss \(\mathcal{L}_{pcl}\)은 다음과 같이 정규화된 weighting parameters \(\{w_i'\}_{i=1}^L\)로 positive pair의 당기는 힘을 조정하여 공식화할 수 있다.

\[\begin{equation} \mathcal{L}_{pcl} = - \frac{1}{L} \sum_{i=1}^L \log \frac{w_i' \cdot e^{y_i \cdot z_i / \tau}}{w_i' \cdot e^{y_i \cdot z_i / \tau} + \frac{1}{L} \sum_{j \ne i} e^{y_i \cdot z_j / \tau}} \\ \sum_{i=1}^N w_i' = 1 \end{equation}\]

Negative pair은 $1/L$로 균형을 맞춘다. 그렇지 않으면 negative pair가 \(\mathcal{L}_{cl}\)에 비해 너무 클 것이다.

Experiments

• 데이터셋: ADE20K, CelebA-HQ (semantic 이미지 합성) / CUB-200, MS-COCO (text-to-image 합성)
• Evaluation Metrics: FID (이미지 품질), PSNR (재구성 정확도)
• Implementation Details
  • VQ-GAN을 따름 ($H \times W = 16 \times 16$, $N = 1024$)
  • 이미지 재구성과 이미지 생성 모두 이미지 크기 256$\times$256를 적용
  • 마스킹 비율은 40%

1. Quantitative Evaluation

다음은 autoregressive model의 semantic 이미지 합성과 diffusion model의 text-to-image 합성 결과이다.

2. Qualitative Evaluation

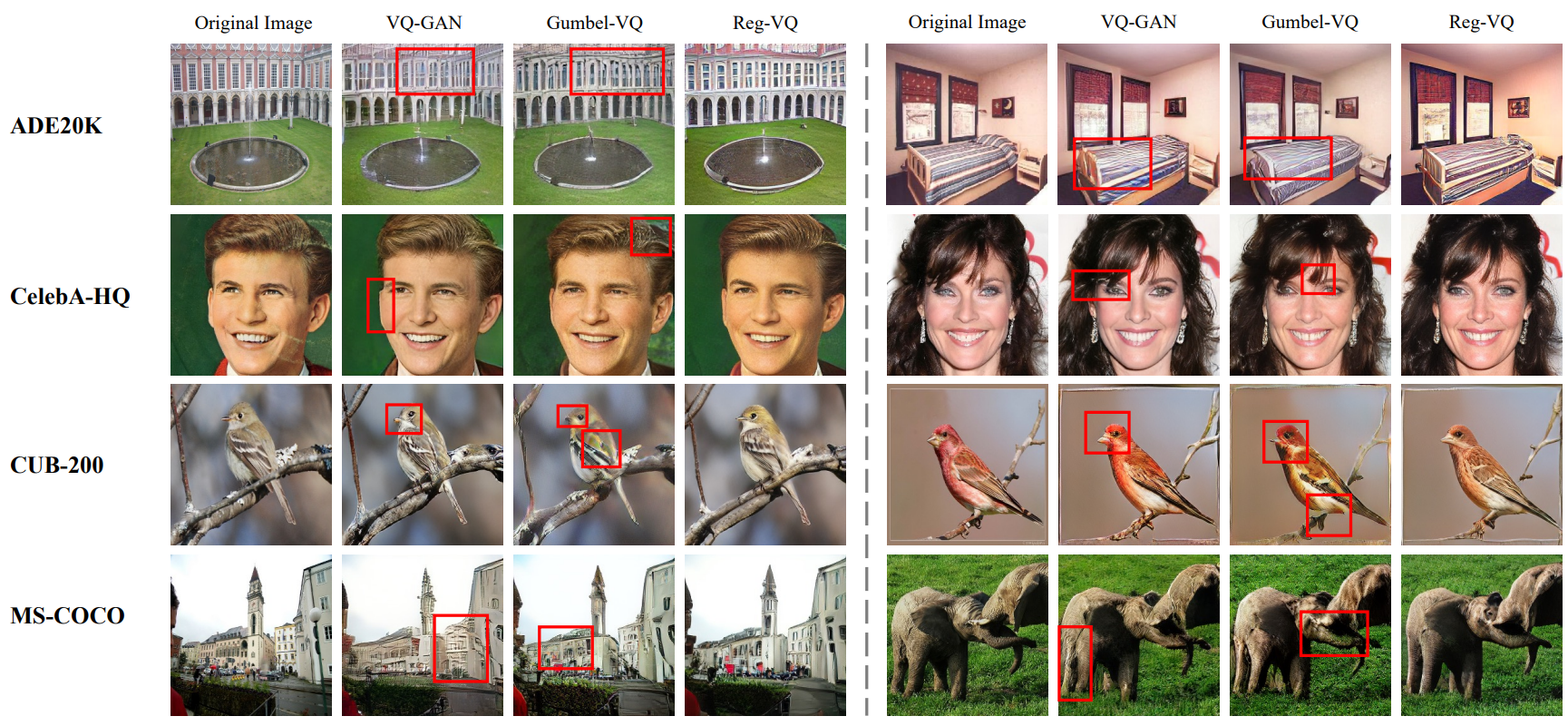
다은은 다양한 quantization 방법의 재구성 이미지이다. 빨간색 박스는 재구성 아티팩트를 강조한 것이다.

다음은 semantic 이미지 합성과 text-to-image 합성의 예시이다.

3. Ablation Study

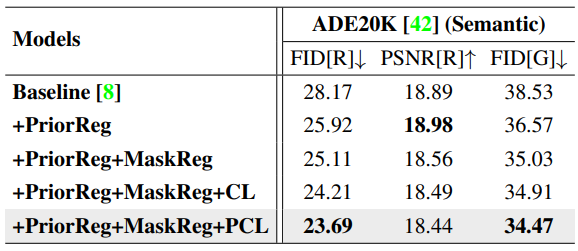
다음은 regularized quantization을 평가하기 위해 진행한 ablation study 결과이다.

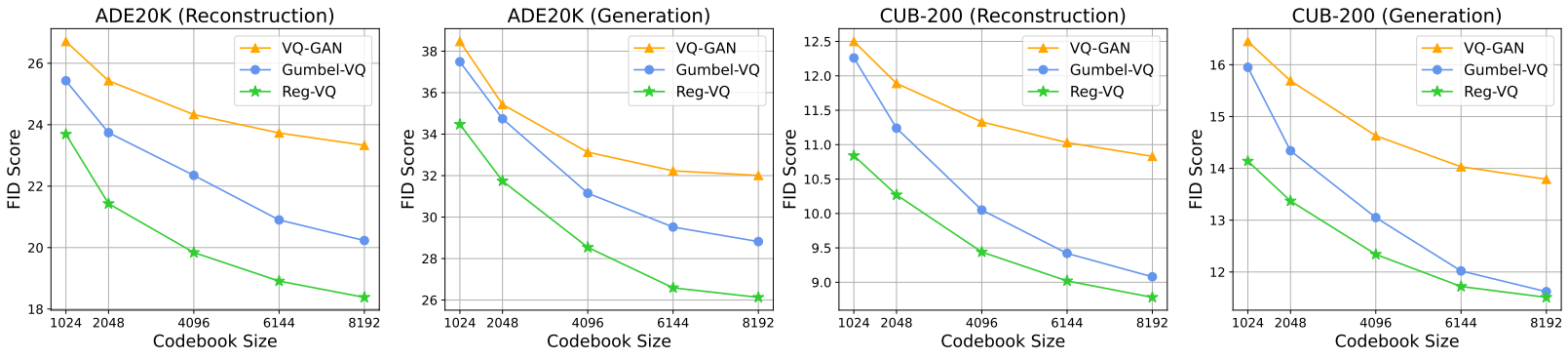
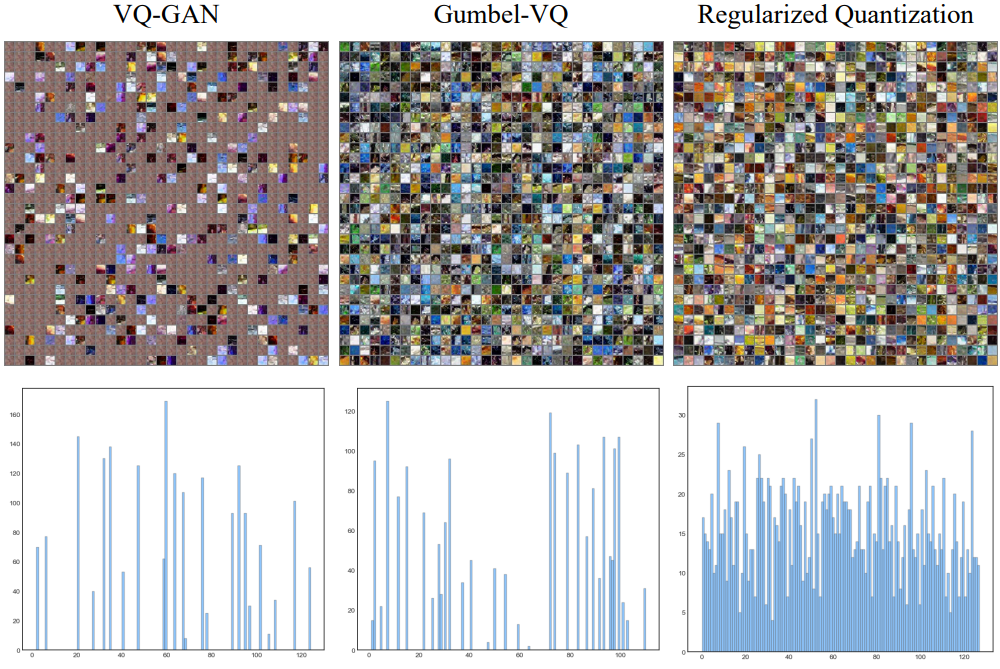
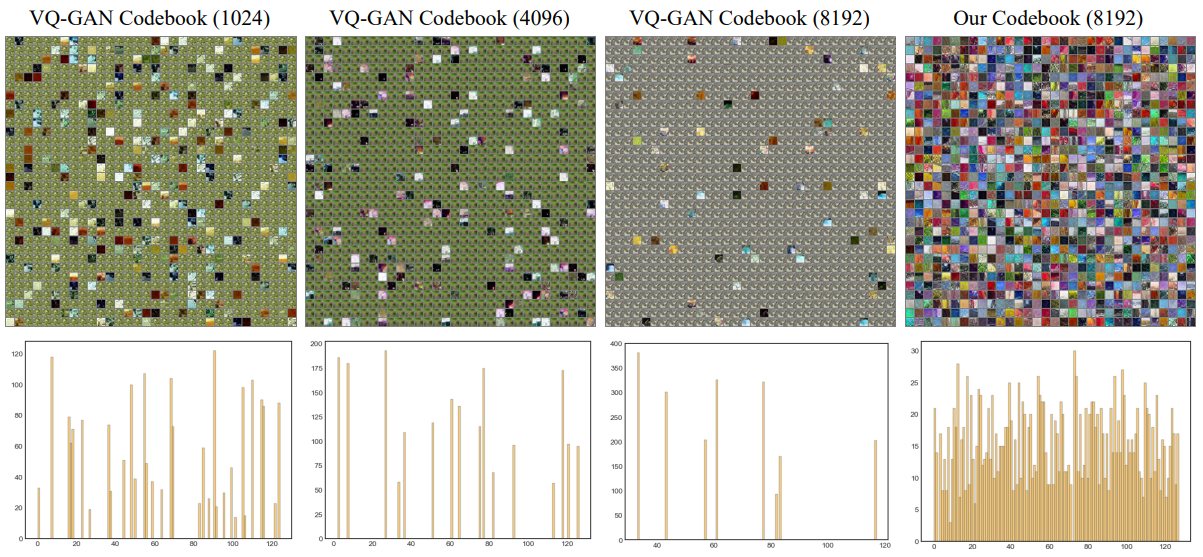
다음은 ADE20K에서의 다양한 크기의 codebook을 시각화한 것이다.

다음은 다양한 codebook 크기가 이미지 재구성과 이미지 생성에 미치는 영향을 나타낸 그래프이다.