[논문리뷰] ReconX: Reconstruct Any Scene from Sparse Views with Video Diffusion Model
arXiv 2024. [Paper] [Page]
Fangfu Liu, Wenqiang Sun, Hanyang Wang, Yikai Wang, Haowen Sun, Junliang Ye, Jun Zhang, Yueqi Duan
Tsinghua University | HKUST
29 Aug 2024

Introduction
최근, 빠른 렌더링 속도와 높은 품질을 갖춘 효율적이고 표현력이 뛰어난 3DGS를 기반으로, sparse view 이미지에서 3D 장면을 재구성하기 위한 여러 방법들이 제안되었다. Feature 추출 모듈에서 장면 prior를 학습하여 유망한 interpolation 결과를 얻을 수 있지만, 장면을 충분히 캡처하지 못하면 여전히 잘못된 최적화 문제가 발생한다. 결과적으로, 특히 보이지 않는 영역에서 3D 장면을 렌더링할 때 심각한 아티팩트와 비현실적인 이미지가 렌더링되는 경우가 많다.
이러한 한계를 해결하기 위해, 본 논문은 본질적으로 모호한 재구성 문제를 생성 문제로 재구성하는 새로운 3D 장면 재구성 패러다임인 ReconX를 제안하였다. 핵심 통찰력은 사전 학습된 대규모 video diffusion model의 강력한 generative prior를 활용하여 다운스트림 재구성 task에 대한 더 많은 observation을 생성하는 것이다.
현재 video diffusion model은 생성된 2D 프레임에서 3D 뷰 일관성이 좋지 않아 고품질 3D 장면을 복구하는 것이 여전히 어렵다. 저자들은 이론적 분석을 토대로, 3D 구조 guidance를 동영상 생성 프로세스에 통합하여 under-determined인 3D 생성 문제와 완전히 관찰된 3D 재구성 간의 격차를 메우는 잠재력을 탐구하였다.
구체적으로, sparse한 이미지들이 주어지면, 포즈가 필요 없는 스테레오 재구성 방법을 통해 먼저 글로벌 포인트 클라우드를 구축한다. 그런 다음, 포인트 클라우드를 cross-attention layer의 3D 조건으로 사용하기 위해 풍부한 컨텍스트 표현 공간으로 인코딩한다. 이를 통해 video diffusion model이 디테일이 보존된 3D 일관된 새로운 observation을 합성하도록 가이드한다. 마지막으로, 생성된 동영상에서 3D 장면을 Gaussian splatting을 통해 재구성하며, 이 때 3D confidence-aware 및 robust한 장면 최적화 체계를 사용하여 동영상 프레임의 불확실성을 효과적으로 줄인다.
ReconX는 높은 품질과 일반화 측면에서 기존 방법을 능가하여 video diffusion model에서 복잡한 3D 세계를 만들 수 있는 엄청난 잠재력을 보여주었다.
Motivation
본 논문은 매우 sparse한 뷰의 이미지들에서 3D 장면 재구성과 novel view synthesis (NVS)의 근본적인 문제에 초점을 맞추었다. 대부분의 기존 방법들은 관찰된 영역과 새로운 영역 간의 차이를 채우기 위해 3D prior과 기하학적 제약 (ex. depth, normal, cost volume)을 활용하였다. 이러한 방법들은 종종 불충분한 시점과 그로 인한 재구성 프로세스의 불안정성이라는 본질적인 문제로 인해 입력 시점에서 볼 수 없는 영역에서 고품질 이미지를 생성하는 데 어려움을 겪는다. 이를 해결하기 위해 자연스러운 아이디어는 더 많은 observation을 생성하여 under-determined인 3D 생성 문제를 완전히 제한된 3D 재구성 설정으로 축소하는 것이다.
최근 video diffusion model은 3D 구조를 특징으로 하는 동영상 클립을 합성하는 데 유망한 것으로 나타났다. 이는 저자들이 대규모 사전 학습된 video diffusion model의 강력한 generative prior를 활용하여 sparse view 재구성을 위한 시간적으로 일관된 동영상 프레임을 생성하도록 영감을 주었다.
하지만, 동영상 프레임 간의 3D 뷰 일관성이 좋지 않아 3DGS 학습 프로세스가 크게 제한되는 주요 문제가 존재한다. 저자들은 동영상 생성 내에서 3D 일관성을 달성하기 위해 먼저 3D 뷰 분포에서 video diffusion modeling을 분석하였다. $x$를 세계의 모든 3D 장면에서 렌더링된 2D 이미지의 집합이라고 하고 $q(x)$를 렌더링 데이터 $x$의 분포라고 하면, divergence $\mathcal{D}$를 최소화하는 것이 목표이다.
\[\begin{equation} \min_{\theta \in \Theta, \psi \in \Psi} \mathcal{D} (q(x) \| p_{\theta, \psi} (x)) \end{equation}\]여기서 \(p_{\theta, \psi}\)는 backbone의 파라미터 $\theta$와 모든 데이터가 공유하는 임베딩 함수 $\psi$로 parameterize된 diffusion model이다. Video diffusion model에서 이들은 이미지 기반 조건을 추가하기 위해 CLIP 모델 $g$를 선택하였다 (즉, $\psi = g$).
그러나 sparse view 3D 재구성에서 제한된 2D 이미지만을 조건으로 사용하면 $q(x)$를 근사하는 데 충분한 guidance를 제공할 수 없다. 저자들은 보다 최적의 솔루션을 찾기 위해 3D prior $\mathcal{F}$를 통합할 가능성을 탐구하고 다음과 같은 이론적 공식을 도출하였다.
Proposition 1. $\theta^\ast$와 $\psi^\ast = g^\ast$가 이미지 기반 조건부 diffusion 방식의 최적해이고 \(\tilde{\theta^\ast}\)와 \(\tilde{\psi^\ast} = \{g^\ast, \mathcal{F}^\ast\}\)가 3D prior를 갖는 diffusion 방식의 최적해라고 하자. Divergence $\mathcal{D}$가 볼록하고 임베딩 함수 공간 $\Psi$에 모든 측정 가능한 함수가 포함된다고 가정하면
\[\begin{equation} \mathcal{D} \, (q(x) \| p_{\tilde{\theta^\ast}, \tilde{\psi^\ast}} (x)) < \mathcal{D} \, (q(x) \| p_{\theta^\ast, \psi^\ast} (x)) \end{equation}\]가 성립한다.
증명)
$\mathcal{D}$가 볼록하므로 Jensen’s inequality $\mathcal{D}(\mathbb{E}[X]) \le \mathbb{E}[\mathcal{D}(X)]$에 의해 다음 식이 성립한다. $$ \begin{aligned} \mathcal{D} (q(x) \| p_{\tilde{\theta^\ast}, \tilde{\psi^\ast}} (x)) &= \mathcal{D} (\mathbb{E}_{q(s)} q(x \vert s) \| \mathbb{E}_{q(s)} p_{\tilde{\theta^\ast}, \tilde{\psi^\ast}} (x \vert s)) \\ &\le \mathbb{E}_{q(s)} \mathcal{D} (q(x \vert s) \| p_{\tilde{\theta^\ast}, \tilde{\psi^\ast}} (x \vert s)) \\ &= \mathbb{E}_{q(s)} \mathcal{D} (q(x \vert s) \| p_{\tilde{\theta^\ast}, g^\ast, \mathcal{F}^\ast} (x \vert s)) \end{aligned} $$ 여기서 $s$는 특정 장면을 나타내며, $q(x \vert s)$는 주어진 장면 $s$에 대한 렌더링 데이터 $x$의 조건부 분포이다. $\tilde{\theta^\ast}$, $g^\ast$, $\mathcal{F}^\ast$의 정의에 의해 다음 식이 성립한다. $$ \begin{aligned} \mathbb{E}_{q(s)} \mathcal{D} \, (q(x \vert s) \| p_{\tilde{\theta^\ast}, g^\ast, \mathcal{F}^\ast} (x \vert s)) &= \min_{\theta, g, \mathcal{F}} \mathbb{E}_{q(s)} \mathcal{D} \, (q (x \vert s) \| p_{\theta, g, \mathcal{F}} (x \vert s)) \\ &= \min_\theta \mathbb{E}_{q(s)} \min_{g(s), \mathcal{F}(s)} \mathcal{D} \, (q (x \vert s) \| p_{\theta, g(s), \mathcal{F}(s)} (x)) \\ &= \min_\theta \mathbb{E}_{q(s)} \min_{g, E} \mathcal{D} \, (q (x \vert s) \| p_{\theta, g, E} (x)) \end{aligned} $$ 여기서 $E$는 3D 구조 조건부 체계의 3D 인코더이며, 이미지 기반 조건부 체계와 중복되는 임베딩이다. (즉, $\psi = \{g, E(\varnothing)\}$)
임의의 장면 $s$에 대하여 $q(x \vert s)$를 근사하는 것은 인코더 $E$만 튜닝하면 되기 때문에 $q(x)$를 근사하는 것보다 간단하다. $$ \begin{equation} \min_E \mathcal{D} \, (q(x \vert s) \| p_{\theta, g, E} (x)) < \min_E \mathcal{D} \, (q(x) \| p_{\theta, g, E} (x)) \end{equation} $$ 위의 식들을 모두 합치고 정리하면 다음과 같다. $$ \begin{aligned} \mathcal{D} \, (q(x) \| p_{\tilde{\theta^\ast}, \tilde{\psi^\ast}} (x)) &\le \mathbb{E}_{q(s)} \mathcal{D} \, (q(x \vert s) \| p_{\tilde{\theta^\ast}, g^\ast, \mathcal{F}^\ast} (x \vert s)) \\ &= \min_\theta \mathbb{E}_{q(s)} \min_{g, E} \mathcal{D} \, (q (x \vert s) \| p_{\theta, g, E} (x)) \\ &< \min_{\theta, g, E} \mathcal{D} \, (q (x) \| p_{\theta, g, E} (x)) = \min_{\theta, g, E(\varnothing)} \mathcal{D} \, (q (x) \| p_{\theta, g, E(\varnothing)} (x)) \\ &= \min_{\theta, \psi} \mathcal{D} \, (q (x) \| p_{\theta, \psi} (x)) = \mathcal{D} \, (q(x) \| p_{\theta^\ast, \psi^\ast} (x)) \end{aligned} $$ 따라서, Proposition 1이 성립한다.
따라서 저자들은 diffusion process에 3D 구조 guidance를 통합하여 본질적으로 모호한 재구성 문제를 생성 문제로 재구성하였다.
Method
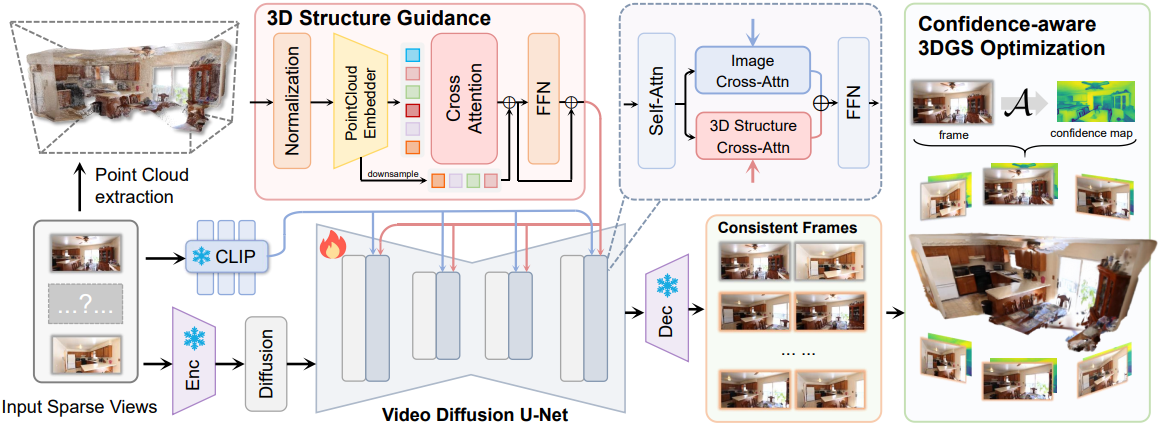
1. Overview of ReconX
- 입력: $K$개의 sparse view 이미지 \(\mathcal{I} = \{I^i\}_{i=1}^K\), (\(I^i \in \mathbb{R}^{H \times W \times 3}\))
- 목표: 보이지 않는 시점의 새로운 뷰를 합성할 수 있는 3D 장면을 재구성
- $\mathcal{I}$에서 글로벌 포인트 클라우드 \(\mathcal{P} = \{p_i, 1 \le i \le N\} \in \mathbb{R}^{N \times 3}\)을 구축
- $\mathcal{P}$를 구조 guidance $\mathcal{F}(\mathcal{P})$로 3D 컨텍스트 표현 공간 $\mathcal{F}$에 projection
- $\mathcal{F}(\mathcal{P})$를 video diffusion process에 주입하여 3D 일관된 동영상 프레임 \(\mathcal{I}^\prime = \{I^i\}_{i=1}^{K^\prime}\)를 생성. ($K^\prime > K$)
- 생성된 동영상 간의 불일치로 인해 발생하는 아티팩트를 완화하기 위해, DUSt3R 모델의 confidence map \(\mathcal{C} = \{\mathcal{C}^i\}_{i=1}^{K^\prime}\)와 LPIPS loss를 활용하여 robust한 3D 재구성을 달성
이런 식으로 video diffusion model의 모든 힘을 발휘하여 매우 sparse한 뷰에서 복잡한 3D 장면을 재구성할 수 있다.
2. Building the 3D Structure Guidance
이론적 분석을 토대로 DUSt3R를 활용하여 3D 구조 guidance $\mathcal{F}$를 구축한다.
- $K$개의 입력 뷰의 연결 그래프 \(\mathcal{G} (\mathcal{V}, \mathcal{E})\)를 구성한다. 여기서 vertex들 $\mathcal{V}$와 각 edge $e = (n, m) \in \mathcal{E}$는 이미지 $I^n$과 $I^m$이 시각적 콘텐츠를 공유함을 나타낸다.
- $\mathcal{G}$를 사용하여 글로벌하게 정렬된 포인트 클라우드 $\mathcal{P}$를 복구한다.
- 각 이미지 쌍 $e = (n, m)$에 대해 쌍별 point map $P^{n,n}$, $P^{m,n}$과 이에 대응되는 confidence map $\mathcal{C}^{n,n}, \mathcal{C}^{m,n} \in \mathbb{R}^{H \times W \times 3}$을 예측한다.
모든 쌍별 예측을 공유 좌표 프레임으로 회전하는 것을 목표로 하기 때문에 각 쌍 $e$와 연관된 transformation matrix $T_e$와 scaling factor $\sigma_e$를 도입하여 글로벌 포인트 클라우드 $\mathcal{P}$를 다음과 같이 최적화한다.
\[\begin{equation} \mathcal{P}^\ast = \underset{\mathcal{P}, \mathcal{T}, \sigma}{\arg \min} \sum_{e \in \mathcal{E}} \sum_{v \in e} \sum_{i=1}^{HW} \mathcal{C}_i^{v,e} \| \mathcal{P}_i^v - \sigma_e T_e P_i^{v,e} \| \end{equation}\]포인트 클라우드 $\mathcal{P}$를 정렬한 후, video diffusion model의 latent feature와 더 나은 상호 작용을 위해 transformer 기반 인코더를 통해 3D 컨텍스트 표현 공간 $\mathcal{F}$로 projection한다. 구체적으로, 학습 가능한 임베딩 함수와 cross-attention 인코딩 모듈을 사용하여 $\mathcal{P}$를 latent code에 임베딩한다.
\[\begin{equation} \mathcal{F} (\mathcal{P}) = \textrm{FFN} (\textrm{CrossAttn} (\textrm{PosEmb} (\tilde{\mathcal{P}}), \textrm{PosEmb} (\mathcal{P}))) \end{equation}\]여기서 \(\tilde{\mathcal{P}}\)는 입력 포인트를 컴팩트한 3D 컨텍스트 공간으로 효율적으로 증류하기 위하여 $\mathcal{P}$를 1/8로 다운샘플링한 것이다.
3. 3D Consistent Video Frames Generation
3D 구조 안내 $\mathcal{F} (\mathcal{P})$를 video diffusion process에 통합하여 일관된 3D 프레임을 얻는다. 생성된 프레임과 장면의 고화질 렌더링 뷰 간의 일관성을 달성하기 위해 동영상 interpolation 능력을 활용하여 더 많은 보이지 않는 observation을 복구한다. 첫 번째 프레임과 마지막 입력 프레임은 두 개의 레퍼런스 뷰이다.
구체적으로, 입력으로 sparse view 이미지 \(\mathcal{I} = \{I_\textrm{ref}^i\}_{i=1}^K\)가 주어지면 $T+2$개의 일관된 프레임 \(f(I_\textrm{ref}^{i−1}, I_\textrm{ref}^i) = \{I_\textrm{ref}^{i−1}, I_1, \ldots, I_T, I_\textrm{ref}^i\}\)를 렌더링하는 것을 목표로 한다. $T$는 생성된 새로운 프레임의 수이다.
Spatial layer의 cross-attention을 통해 U-Net 중간 feature \(F_\textrm{in}\)과 상호 작용하여 3D guidance를 video diffusion process에 주입한다.
\[\begin{equation} F_\textrm{out} = \textrm{Softmax} (\frac{QK_g^\top}{\sqrt{d}}) V_g + \lambda_\mathcal{F} \cdot \textrm{Softmax} (\frac{QK_\mathcal{F}^\top}{\sqrt{d}}) V_\mathcal{F} \\ \textrm{where} \; Q = F_\textrm{in} W_Q, \; K_g = g(I_\textrm{ref}) W_K, \; V_g = g(I_\textrm{ref}) W_V, \\ \qquad K_\mathcal{F} = \mathcal{F}(\mathcal{P}) W_K^\prime, \; V_\mathcal{F} = \mathcal{F}(\mathcal{P}) W_V^\prime \end{equation}\]$W_Q$, $W_K$, $W_K^\prime$, $W_V$, $W_V^\prime$은 projection matrix이다. 첫 번째와 마지막 두 개의 뷰 조건 $c_\textrm{view}$를 $g(I_\textrm{ref})$에서 가져오고, 3D 구조 조건 $c_\textrm{struc}$을 $\mathcal{F}(\mathcal{P})$에서 가져온 후, classifier-free guidance를 적용하여 조건을 통합한다. 학습 목적 함수는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{diffusion} = \mathbb{E}_{x \sim p, \epsilon \sim \mathcal{N}(0,I), c_\textrm{view}, c_\textrm{struc}, t} [\| \epsilon - \epsilon_\theta (x_t, t, c_\textrm{view}, c_\textrm{struc}) \|_2^2] \end{equation}\]($x_t$는 학습 데이터의 GT 뷰에서 얻은 latent noise)
4. Confidence-Aware 3DGS Optimization
기존의 3D 재구성 방법은 원래 캘리브레이션된 카메라 메트릭을 사용하여 실제로 촬영한 사진을 처리하도록 설계되었기 때문에 생성된 동영상에 직접 적용하는 것은 이미지의 불확실성으로 인해 일관된 장면을 복구하기에 완벽하지 않다. 불확실성 문제를 완화하기 위해 저자들은 confidence-aware 3DGS 메커니즘을 채택하여 복잡한 장면을 재구성하였다.
이미지별 불확실성을 모델링하는 최근의 접근 방식과 달리 본 논문은 일련의 프레임 간의 global alignment에 중점을 두었다. 생성된 프레임 \(\{I^i\}_{i=1}^{K^\prime}\)에 대하여, 생성된 뷰와 GT 뷰 $i$에 대한 픽셀별 색상 값을 \(\hat{C}_i\)와 $C_i$라 하자. 저자들은 3DGS에서 픽셀 값을 가우시안 분포로 모델링하였으며, 여기서 $I^i$의 평균과 분산은 각각 $C_i$와 $\sigma_i$이다. 분산 $sigma_i$는 생성된 뷰와 실제 뷰 사이의 불일치를 측정한다. 목표는 모든 프레임에서 다음과 같은 negative log-likelihood를 최소화하는 것이다.
\[\begin{equation} \mathcal{L}_{I_i} = - \log \bigg( \frac{1}{\sqrt{2 \pi \sigma_i^2}} \exp \bigg( - \frac{\| \hat{C}_i^\prime - C_i \|_2^2}{2 \sigma^2} \bigg) \bigg) \\ \textrm{where} \; \hat{C}_i^\prime = \mathcal{A} (\hat{C}_i, \{\hat{C}_i\}_{i=1}^{K^\prime} \backslash \hat{C}_i) \end{equation}\]$\mathcal{A}$는 global alignment 함수이다. 저자들은 경험적 연구를 통해 DUSt3R의 transformer 디코더에서 잘 정렬된 매핑 함수 $\mathcal{A}$를 찾았는데, 이는 생성된 각 프레임 \(\{I_i\}_{i=1}^{K^\prime}\)에 대한 confidence map \(\{\mathcal{C}_i\}_{i=1}^{K^\prime}\)을 구축한다. 구체적으로, 신뢰도 점수는 추정하기 어려운 영역에서 낮아지는 경향이 있는 반면, 불확실성이 적은 영역에서는 점수가 높아진다. 또한, 아티팩트를 제거하고 시각적 품질을 더욱 향상시키기 위해 LPIPS loss를 도입하였다. Confidence-aware 3DGS loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{conf} = \sum_{i=1}^{K^\prime} \mathcal{C}_i (\lambda_\textrm{RGB} \mathcal{L}_1 (\hat{I}_i, I_i) + \lambda_\textrm{ssim} \mathcal{L}_\textrm{ssim} (\hat{I}_i, I_i) + \lambda_\textrm{lpips} \mathcal{L}_\textrm{lpips} (\hat{I}_i, I_i)) \end{equation}\]Experiments
- 데이터셋: RealEstate-10K, ACID, DL3DV-10K
- 구현 디테일
- 3D reconstruction backbone: DUSt3R
- video diffusion backbone: DynamiCrafter (512$\times$512)
- 1단계: 이미지 cross-attention layer fine-tuning
- step: 2,000
- learning rate: $1 \times 10^{-4}$
- 2단계: Spatial layer fine-tuning
- step: 30,000
- learning rate: $1 \times 10^{-5}$
- optimizer: AdamW
- 32개의 프레임을 샘플링하여 학습에 사용
- DynamiCrafter와 마찬가지로 tanh gating으로 \(\lambda_\mathcal{F}\)를 적응적으로 학습
- 학습은 NVIDIA A800 (80G) GPU 8개에서 2일 소요
- 3DGS 최적화 단계
- 첫 번째와 마지막 프레임의 point map을 글로벌 포인트 클라우드로 사용
- 생성된 32개의 프레임을 모두 사용하여 장면을 재구성
- 원래 3DGS와 다르게 adaptive control을 생략하고 1,000 step만으로 최적화
- \(\lambda_\textrm{rgb}\) = 0.8, \(\lambda_\textrm{ssim}\) = 0.2, \(\lambda_\textrm{lpips}\) = 0.5
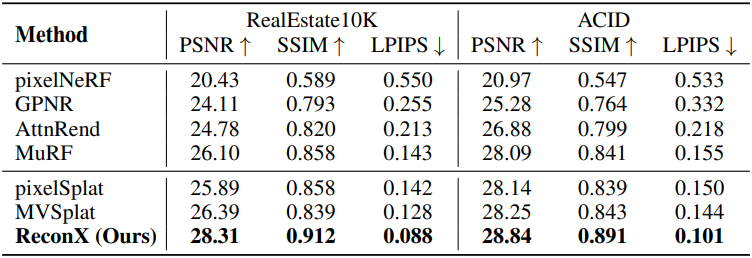
1. Comparison with Baselines
다음은 입력 뷰 사이의 각도 차이가 작은 경우에 대한 결과이다.

다음은 입력 뷰 사이의 각도 차이가 큰 경우에 대한 결과이다.


다음은 RealEstate10K에서 학습된 모델을 NeRF-LLFF와 DTU 데이터셋에서 테스트한 결과이다.


2. Ablation Study
다음은 ablation study 결과이다.

