[논문리뷰] MeshAnything V2: Artist-Created Mesh Generation With Adjacent Mesh Tokenization

ICCV 2025. [Paper] [Page] [Github]
Yiwen Chen, Yikai Wang, Yihao Luo, Zhengyi Wang, Zilong Chen, Jun Zhu, Chi Zhang, Guosheng Lin
S-Lab, Nanyang Technological University | Shengshu | Tsinghua University | Imperial College London | Westlake University
5 Aug 2024

Introduction

본 논문에서는 autoregressive 메쉬 생성의 tokenization 방식에 초점을 맞추고, 메쉬 생성의 효율성과 품질을 향상시키고자 하였다. 본질적으로 순차적인 구조를 갖는 텍스트와 달리 메쉬는 3차원 특성을 가진 그래프 기반 구조이다. 주어진 메쉬를 1차원 토큰 시퀀스로 표현하는 방법은 무수히 많기 때문에, tokenization 방식의 영향력은 메쉬에 더욱 두드러진다. 따라서 메쉬 tokenization 방식에 대한 연구가 매우 중요하다.

메쉬 tokenization이 autoregressive 메쉬 생성에 미치는 영향은 두 가지 주요 측면에서 고려할 수 있다.

1. 효율성: 메쉬를 더 짧고 간결한 토큰 시퀀스로 표현하면 컨텍스트 길이가 줄어들어 메모리와 계산 복잡도가 감소한다.
2. 규칙성: 짧은 토큰 시퀀스가 ​​메쉬 생성에 항상 더 나은 것은 아니며, 시퀀스의 규칙성과 패턴 일관성은 효과적인 시퀀스 학습에 필수적이다.

효과적인 메쉬 tokenization은 고품질의 효율적인 메쉬 생성을 위해 효율성과 규칙성의 균형을 맞춰야 한다.

위의 내용을 고려하여, 본 논문은 메쉬를 생성하는 고급 모델인 MeshAnything V2를 소개한다. 이 모델은 성능과 효율성을 모두 향상시키기 위한 몇 가지 주요 개선 사항을 포함하고 있다. MeshAnything V2의 핵심은 혁신적인 Adjacent Mesh Tokenization (AMT)이다. AMT는 각 면을 기존의 세 개의 vertex 대신 하나의 vertex로 표현하여 tokenization 프로세스를 최적화한다. AMT는 인접한 면을 단 하나의 vertex만 사용하여 인코딩하여 시퀀스 길이를 크게 줄인다. 인접한 면을 식별할 수 없는 경우, 특수 토큰 ‘&’를 사용하여 이러한 중단을 표시하고, 모델은 인코딩되지 않은 면부터 다시 시작할 수 있다.

이전 메쉬 생성 방법에서는 사용자가 모델에서 생성되는 면의 개수를 제어할 수 없어 요구 사항을 충족하지 못하는 메쉬가 생성되는 경우가 많았다. 이 문제를 해결하기 위해, 사용자가 대략적인 면의 개수를 지정할 수 있도록 하는 면 개수 조건을 도입하여 생성된 메쉬가 원하는 사양에 부합하도록 보장하엿다. 또한, inference 중 AMT의 robustness를 향상시키기 위해, 모델이 ‘&’ 토큰 바로 뒤에 또 다른 ‘&’ 토큰을 생성하는 등 유효하지 않은 토큰을 생성하는 것을 방지하는 Masking Invalid Predictions 기능을 통합했다.

Method

1. Adjacent Mesh Tokenization (AMT)

Tokenization은 텍스트, 이미지, 오디오 등 다양한 데이터 형식을 토큰 시퀀스로 처리하기 때문에 시퀀스 학습에 매우 중요한 부분이다. 처리된 토큰은 시퀀스 모델 학습을 위한 실제 입력으로 사용된다. Inference 과정에서 시퀀스 모델은 토큰 시퀀스를 생성하고, 이 토큰 시퀀스는 이후 목표 데이터 형식으로 detokenize된다. 따라서 tokenization은 시퀀스 학습에서 중요한 역할을 하며, 시퀀스 모델이 학습하는 데이터 시퀀스의 품질을 결정한다.

먼저 이전 방법들에서 사용된 tokenization 방법을 살펴보자. 메쉬 $\mathcal{M}$이 주어지면, vertex들을 먼저 z-y-x 좌표를 기준으로 오름차순으로 정렬한다. 여기서 z는 수직축을 나타낸다. 다음으로, 면들을 가장 낮은 vertex 인덱스 순으로 정렬하고, 그 다음으로 낮은 vertex 인덱스 순으로 정렬한다. 메쉬는 정렬된 면들의 시퀀스로 간주된다.

\[\begin{equation} \mathcal{M} := (f_1, f_2, \ldots, f_N) \end{equation}\]

그러면 각 $f_i$는 세 개의 vertex $v$의 순서 있는 시퀀스로 표현된다.

\[\begin{equation} f_i := (v_{i1}, v_{i2}, v_{i3}) \end{equation}\]

$v_{i1}$, $v_{i2}$, $v_{i3}$는 이미 정렬되어 있고 순서가 고정되어 있다.

\[\begin{equation} \mathcal{M} := ((v_{11}, v_{12}, v_{13}), \ldots, (v_{N1}, v_{N2}, v_{N3})) = \textrm{Seq}_V \end{equation}\]

정렬 덕분에 생성된 \(\textrm{Seq}_V\)는 고유하며, 길이는 메쉬에 포함된 면의 개수의 3배이다. 각 vertex가 속한 면의 개수만큼 반복되므로 \(\textrm{Seq}_V\)에 상당한 양의 중복 정보가 포함되어 있음을 알 수 있다.

본 논문은 이전 방법들보다 더 컴팩트하고 잘 구조화된 \(\textrm{Seq}_V\)를 얻기 위해 Adjacent Mesh Tokenization (AMT)를 제안하였다. 저자들의 주요 관찰은 \(\textrm{Seq}_V\)의 주요 중복성이 각 면을 세 개의 vertex로 표현하는 데서 비롯된다는 것이다. 이로 인해 이미 방문한 vertex가 \(\textrm{Seq}_V\)에 중복되어 나타난다. 따라서 AMT는 가능한 한 각 면을 하나의 vertex만 사용하여 표현하는 것을 목표로 한다.

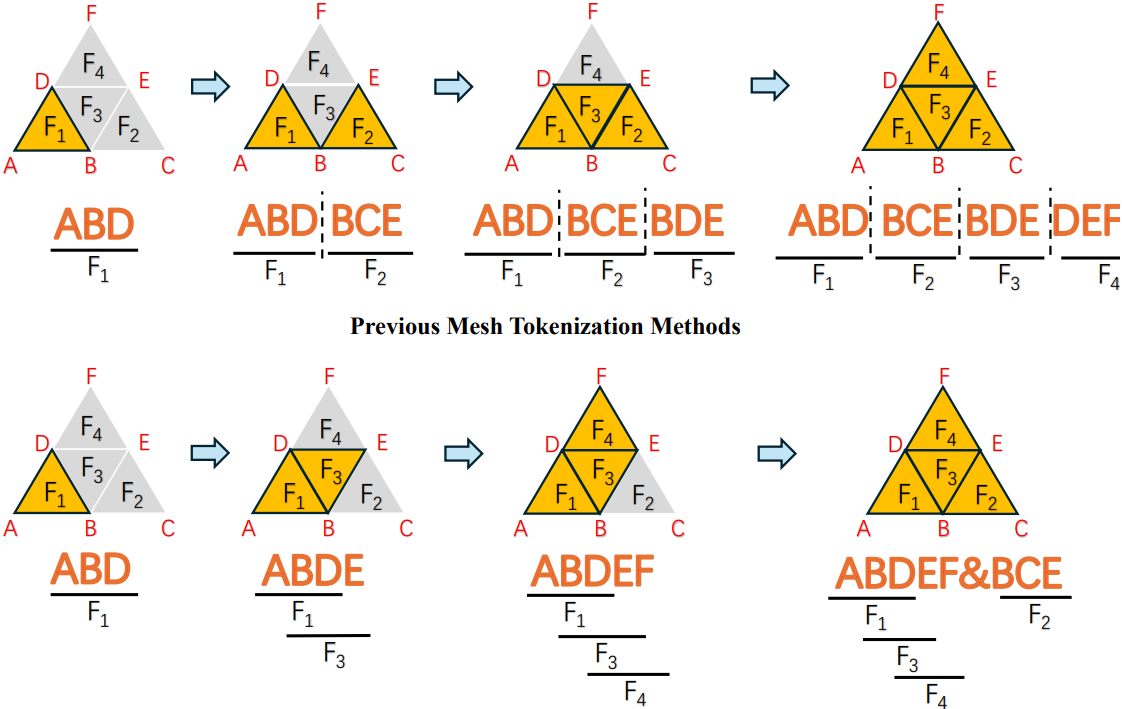
AMT는 tokenization 중에 추가 vertex를 하나만 사용하여 인접한 면을 효율적으로 인코딩한다. 위 그림의 마지막 단계에 표시된 대로 인접한 면을 사용할 수 없는 경우, AMT는 이를 나타내는 특수 토큰 “&”를 시퀀스에 삽입하고 아직 인코딩되지 않은 면에서 프로세스를 다시 시작한다. Detokenize하려면 tokenization 알고리즘을 반대로 실행하면 된다.

특수 토큰 “&”가 거의 사용되지 않는 이상적인 경우, AMT는 이전 방법으로 얻은 \(\textrm{Seq}_V\)의 길이를 거의 1/3로 줄일 수 있다. 물론, 메쉬의 각 면이 다른 면과 완전히 분리된 극단적인 경우에는 AMT의 성능이 이전 방법보다 떨어진다. 그러나 메쉬 생성에 사용되는 데이터셋은 사람이 직접 생성한 것이므로 메쉬는 일반적으로 잘 구조화된 topology를 갖는다. 따라서 AMT의 전반적인 성능은 이전 방법보다 훨씬 뛰어나다. 예를 들어, AMT는 Objaverse test set에서 \(\textrm{Seq}_V\)의 길이를 평균 절반으로 줄일 수 있다.

Vertices Swap

두 면 $f_1$과 $f_2$를 고려하자.

\[\begin{equation} f_1 = (v_1, v_2, v_3), \quad f_2 = (v_1, v_3, v_4) \end{equation}\]

이 두 면은 edge $(v_1, v_3)$으로 연결되어 있다. 먼저 $f_1$을 $(v_1, v_2, v_3)$으로 표현한다고 가정하면, $f_1$과 $f_2$가 실제로 인접해 있음에도 불구하고 $f_2$가 $v_2$를 포함하지 않기 때문에 AMT가 중단된다. 이 문제를 해결하기 위해 vertex를 교환하는 특수 토큰 “\(\$\)“를 도입한다. “\(\$\)” 토큰이 vertex 앞에 나타나면 다음 면이 이전 면의 마지막 두 vertex가 아닌 첫 번째 vertex와 마지막 vertex로 구성됨을 나타낸다. 예를 들어, 토큰 시퀀스 \((v_1, v_2, v_3, \$, v_4)\)는 메쉬가 두 면, 즉 $(v_1, v_2, v_3)$과 $(v_1, v_3, v_4)$로 구성됨을 의미한다.

Swap 연산은 추가적인 특수 토큰을 도입하지만, 중단 횟수를 줄이고 토큰 시퀀스를 효과적으로 단축한다. 특수 토큰을 추가하면 시퀀스 학습의 난이도가 높아질 수 있지만, 실험에서는 눈에 띄는 영향은 없었다고 한다.

메쉬 tokenization에서의 정렬

이전 방법과 AMT는 모두 메쉬의 vertex와 면을 처음에 정렬한다. 주요 목표는 메쉬 데이터를 고정된 패턴의 시퀀스로 처리하여 시퀀스 모델의 학습을 용이하게 하는 것이다. AMT에서는 이러한 디자인을 유지하기 위해 여러 선택지가 있을 때마다 정렬된 목록에서 더 빠른 인덱스를 가진 면을 일관되게 선택한다. 또한, 이러한 설계 덕분에 AMT가 처리하는 토큰 시퀀스는 각 메쉬마다 고유하다. 또한, AMT는 가능한 한 인접한 면을 우선적으로 방문한다. 반면, 이전 방법들은 정렬된 순서를 단순하게 따르기 때문에 공간적으로 멀리 떨어진 vertex들이 시퀀스에서 인접한 토큰 시퀀스를 생성하는 경우가 많아 시퀀스 복잡성이 증가할 가능성이 있다. AMT는 이전 방법들에 비해 속도와 메모리 사용량 측면에서 상당한 이점을 제공하며, 정확도도 향상되어 AMT로 생성된 시퀀스가 ​​더욱 간결하고 구조화되어 있다.

AMT와 VQ-VAE의 사용

\(\textrm{Seq}_V\)를 얻은 후, 메쉬 생성 방법은 시퀀스 학습을 위해 토큰 시퀀스로 처리해야 한다. 이를 위해 MeshGPT에서는 VQ-VAE를 학습시킨 다음, VQ-VAE의 quantize된 feature를 transformer의 입력으로 사용하였다. 반면, MeshXL은 VQ-VAE를 버리고 vertex의 discretize된 좌표를 토큰 인덱스로 직접 사용하였다.

VQ-VAE를 사용하든 사용하지 않든 AMT의 효과에 영향을 미치지 않는다. 이는 AMT가 이 방법들보다 먼저 작동하기 때문이다. 예를 들어, VQ-VAE를 사용하는 경우 AMT는 먼저 $\mathcal{M}$을 나타내는 \(\textrm{Seq}_V\)를 줄이고, 단축된 \(\textrm{Seq}_V\)는 VQ-VAE로 임베딩 시퀀스로 quantize된다.

2. MeshAnything V2

MeshAnything을 따라, MeshAnything V2 또한 주어진 shape $\mathcal{S}$에 맞춰 정렬된 메쉬 $\mathcal{M}$을 생성하는 것을 목표로 하며, 다양한 3D 에셋 제작 파이프라인과 통합하여 고도로 제어 가능한 메쉬 생성을 달성할 수 있다. 즉, $p(\mathcal{M} \vert \mathcal{S})$ 분포를 학습하는 것을 목표로 한다.

MeshAnything에서와 같이 V2는 포인트 클라우드를 조건 입력 $\mathcal{S}$로 사용한다. 또한 MeshAnything에서 수집한 동일한 포인트 클라우드-메쉬 데이터 쌍 $(\mathcal{M}, \mathcal{S})$를 사용하였다. 대상 분포 $p(\mathcal{M} \vert \mathcal{S})$는 MeshAnything에서와 동일한 크기와 아키텍처를 가진 decoder-only transformer로 학습되었다. $\mathcal{S}$를 transformer에 주입하려면 먼저 사전 학습된 포인트 클라우드 인코더로 고정 길이 토큰 시퀀스 \(\mathcal{T}_S\)로 인코딩한 다음 transformer의 토큰 시퀀스 prefix로 설정한다. 그런 다음 $\mathcal{M}$을 메쉬 토큰 시퀀스 \(\mathcal{T}_M\)으로 처리한다. 이것은 transformer의 GT 시퀀스로 포인트 클라우드 토큰 시퀀스에 concat된다. Cross-entropy loss로 transformer를 학습시킨 후, \(\mathcal{T}_S\)를 입력하고 transformer가 해당 \(\mathcal{T}_M\)을 autoregressive하게 생성하도록 한 다음, 이를 \(\mathcal{M}\)으로 detokenizea한다.

MeshAnything과 V2의 주요 차이점은 \(\mathcal{T}_M\)을 얻는 방법이다. MeshAnything에서 사용된 단순한 메쉬 tokenization 방법 대신 새로 제안된 AMT로 \(\mathcal{M}\)을 처리하고 더 컴팩트하고 효율적인 시퀀스 \(\textrm{Seq}_V\)를 얻는다. MeshXL를 따라 VQ-VAE를 버리고 \(\textrm{Seq}_V\)에서 discretize된 좌표를 토큰 인덱스로 직접 사용한다. 그런 다음 AMT 시퀀스에서 “&”를 나타내기 위해 새로 초기화된 codebook entry를 추가한다. 마지막으로 좌표 토큰 시퀀스와 “&”에 대한 특수 토큰을 순차적으로 결합하여 transformer 입력에 대한 메쉬 토큰 시퀀스 \(\mathcal{T}_M\)을 얻는다.

Transformer가 AMT 시퀀스 패턴을 쉽게 학습할 수 있도록, MeshAnything에서 사용된 absolute positional encoding 외에도 AMT를 위한 다음과 같은 임베딩을 추가한다.

• 3개의 vertex로 면을 표현할 때는 세 개의 새로운 vertex에 대한 특정 임베딩을 추가한다.
• 하나의 vertex로 면을 표현할 때는 하나의 새로운 vertex에 대해 다른 임베딩을 추가한다.
• “&” 토큰에 대한 별도의 임베딩을 사용한다.

면 개수 조건

일부 애플리케이션에서는 대략적인 면 개수 제어가 필요하다는 점을 고려하여 메쉬 생성 시 면 개수 조건을 추가하였다. 구체적으로, 최대 허용 면 개수와 동일한 크기의 embedding book을 초기화했다. 메쉬의 현재 면 개수를 기반으로 이 embedding book에서 해당 임베딩을 검색하여 포인트 클라우드 prefix 뒤에 배치하여 면 개수를 나타낸다. 학습 과정에서 면 개수에 확률 변수를 추가하여 변동성을 높이고 정확한 조건에 대한 overfitting을 방지한. 또한, 조건의 robustness를 더욱 향상시키기 위해 10% 확률로 이 조건을 삭제한다.

Masking Invalid Predictions

PolyGen은 inference 과정에서 Masking Invalid Predictions 기능을 도입했다. PolyGen에서는 vertex를 먼저 생성한 후 면을 생성하고, vertex와 면을 모두 정렬한다. Inference 과정에서 제약 조건을 적용하지 않으면 생성 모델이 시퀀스 구조를 따르지 않는 결과를 생성할 수 있다. 예를 들어 모든 vertex를 완료하기 전에 면을 생성하거나 정렬된 좌표 순서를 위반하는 vertex를 생성할 수 있다. PolyGen은 inference 단계에서 유효하지 않은 logit을 마스킹하여 유효한 결과만 생성되도록 함으로써 이 문제를 해결하였다.

메쉬에서 좌표 정렬이 널리 사용되기 때문에 이 설계는 다른 tokenization 방법에도 적용될 수 있다. 저자들은 AMT 실험에서도 이 방법을 적용했다. 예를 들어, AMT에서는 새 strip을 시작할 때 중단을 허용하기 전에 최소 세 개의 vertex를 생성해야 한다는 규칙을 적용했다.

Experiments

• 구현 디테일
  • Transformer: OPT-350M
  • 포인트 인코더: Michelangelo
  • AMT를 제외한 나머지는 MeshAnything과 동일

1. Ablation Study

다음은 AMT에 대한 ablation study 결과이다.

2. Comparison

다음은 다른 tokenization 방법들과 비교한 결과이다.