[논문리뷰] ERNIE-Music: Text-to-Waveform Music Generation with Diffusion Models

AACL 2023. [Paper]
Pengfei Zhu, Chao Pang, Shuohuan Wang, Yekun Chai, Yu Sun, Hao Tian, Hua Wu
Baidu Inc.
9 Feb 2023

Introduction

자유 형식 텍스트를 기반으로 waveform 음악을 생성하는 문제는 아직 잘 연구되지 않았다. BUTTER와 Mubert와 같은 텍스트 조건부 음악 생성에 대한 여러 연구가 있었지만 자유 형식 텍스트를 기반으로 음악 오디오를 직접 생성할 수는 없다. BUTTER는 제한된 키워드만을 텍스트 조건으로 입력받아 추가적인 후처리 악보 합성 작업이 필요한 symbolic 악보를 생성한다. 보다 풍부한 형태의 텍스트를 처리할 수 있지만 symbolic 음악 생성 작업이기도 하다. Mubert의 음악 작품은 모두 인간 음악가에 의해 만들어진다. 특정 텍스트가 주어지면 미리 정해진 장르 텍스트 레이블을 기준으로 음악을 검색하고 순차적으로 결합한다. 제한된 음악만 만들 수 있으며 다른 음악 세그먼트 간의 전환이 부자연스럽다.

본 논문은 이러한 기존 연구의 단점을 극복하기 위해 diffusion model을 사용하여 waveform 도메인에서 자유 형식의 텍스트를 음악으로 생성하는 최초의 시도인 ERNIE-Music을 제안한다. 대량의 텍스트-음악 데이터셋이 부족한 문제를 해결하기 위해 “댓글 투표” 메커니즘을 활용하여 인터넷에서 데이터를 수집한다. 조건부 diffusion model을 적용하여 음악 waveform을 처리하여 생성 프로세스를 모델링하고 어떤 종류의 텍스트 형식이 모델에 도움이 되는지 연구하여 텍스트 음악 관련성을 더 잘 학습한다. 결과적으로 생성된 음악 샘플은 다양하고 우아하며 관련 연구의 방법보다 훨씬 뛰어나다.

Method

1. Unconditional Diffusion Model

Diffusion model은 데이터 샘플에 noise를 반복적으로 추가하는 forward process와 데이터 샘플을 여러 번 제거하여 실제 데이터 분포에 부합하는 샘플을 생성하는 reverse process로 구성된다. 본 논문은 연속 시간으로 정의된 diffusion model을 채택한다. 분포 $p(x)$에서 데이터 샘플 $x$를 고려하자. Diffusion model은 $t \in [0,1]$인 latent 변수 $z_t$를 활용한다. 로그 신호 대 잡음비 (log SNR) $\lambda_t$는 $\lambda_t = \log [\alpha_t^2 / \sigma_t^2]$으로 정의되며, 여기서 $\alpha_t$와 $\sigma_t$는 noise schedule을 나타낸다. Forward process의 경우 Gaussian noise가 샘플에 반복적으로 추가되어 Markov chain을 충족한다.

\[\begin{aligned} q(z_t \vert x) &= \mathcal{N} (z_t; \alpha_t x, \sigma_t^2 I) \\ q(z_{t'} \vert z_t) &= \mathcal{N} (z_{t'}; (\alpha_{t'} / \alpha_t)z_t, \sigma_{t' \vert t}^2 I) \\ \sigma_{t' \vert t}^2 &= (1 - e^{\lambda_{t'} - \lambda_t}) \sigma_{t'}^2 \end{aligned}\]

Reverse process에서 파라미터 $\theta$ (\(\hat{x}_\theta (z_t, \lambda_t, t) \approx x\))를 사용한 함수 근사는 denoising 절차를 추정한다.

\[\begin{aligned} p_\theta(z_{t'} \vert z_t) &= \mathcal{N}(z_t; \tilde{\mu}_{t \vert t'}(z_{t'}, x), \tilde{\sigma}_{t \vert t'}^2 I) \\ \tilde{\mu}_{t \vert t'}(z_{t'}, x, t') &= e^{\lambda_{t'} - \lambda_t} (\alpha_t / \alpha_{t'}) z_{t'} + (1 - e^{\lambda_{t'} - \lambda_t}) \alpha_t x \end{aligned}\]

$z_1 \sim \mathcal{N} (0,I)$에서 시작하여 latent 변수 $z_t$에 denoising 절차를 적용하면 reverse process 끝에 $z_0 = \hat{x}$를 생성할 수 있다. Denoising model \(\hat{x}_\theta (z_t, \lambda_t, t)\)를 학습시키기 위해 가중 MSE loss가 채택된다.

\[\begin{equation} L = \mathbb{E}_{t \sim [0, 1], \epsilon \sim \mathcal{N}(0,I)} [w(\lambda_t) \| \hat{x}_\theta (z_t, \lambda_t, t) - x \|_2^2 ] \end{equation}\]

여기서 $w(\lambda_t)$는 가중치 함수이며 $\epsilon \sim \mathcal{N}(0,I)$은 noise이다.

2. Conditional Diffusion Model

조건부 diffusion model은 denoising process \(\hat{x}_\theta (z_t, \lambda_t, t, y)\)를 모델링하여 $p(x)$ 대신 분포 $p(x \vert y)$를 근사한다. 여기서 $y$는 조건을 나타낸다. $y$는 이미지, 텍스트, 오디오와 같은 모든 유형의 modality가 될 수 있다. 특히 text-to-music 생성 시나리오에서 $y$는 관련 음악을 생성하도록 모델을 안내하는 텍스트 프롬프트이다.

Model Architecture

Text-to-music 생성의 경우 diffusion process의 조건 $y$는 텍스트이다. 위 그림에서 볼 수 있듯이 전체 모델 아키텍처에는 velocity \(\hat{v}_\theta (z_t, t, y)\)를 모델링하는 조건부 음악 diffusion model과 길이가 $n$인 텍스트 토큰을 $d_E$ 차원의 벡터 표현의 시퀀스 $[s_0; S]$로 매핑하는 텍스트 인코더 $E(\cdot)$가 포함되어 있다. 여기서 $S = [s_1, \cdots, s_n]$이고, $s_i \in \mathbb{R}^{d_E}$이며, $s_0$는 텍스트의 classification 표현이다.

음악 diffusion model의 입력은 latent 변수 $z_t \in \mathbb{R}^{d_c \times d_s}$, timestep $t$ (임베딩 $e_t \in \mathbb{R}^{d_t \times d_s}$로 변환됨)와 텍스트 시퀀스 표현 $[s_0; S] \in \mathbb{R}^{(n+1) \times d_E}$이다. 여기서 $d_c$는 채널 수, $d_s$는 샘플 크기, $d_t$는 타임스텝 임베딩의 feature 크기를 나타낸다. 출력은 추정된 velocity \(\hat{v}_t \in \mathbb{R}^{d_c \times d_s}\)이다.

Latent diffusion model에 대한 이전 연구에서 영감을 받아 주요 구성 요소가 convolutional block과 self-attention block을 쌓은 UNet 아키텍처를 채택한다. 생성 모델은 조건부 분포 $p(x \vert y)$를 추정할 수 있으며 조건부 정보 $y$는 여러 가지 방법으로 생성 모델에 융합될 수 있다.

Diffusion network는 noisy한 latent $z_t$와 조건으로 텍스트 입력이 주어지면 랜덤하게 샘플링된 timestep $t$에서 latent velocity \(\hat{v}_\theta\)를 예측하는 것을 목표로 한다. 조건을 diffusion process에 도입하기 위해 timestep embedding $e_t$와 텍스트 classification 표현 $s_0$에 fuse 연산 $\textrm{Fuse} (\cdot, \cdot)$를 수행하여 text-aware timestep embedding \(e'_t = \textrm{Fuse}(e_t, s_0) \in \mathbb{R}^{d_{t'} \times d_s}\)를 얻는다. 그런 다음 $z’t = (z_t \oplus e’_t) \in \mathbb{R}^{(d{t’} + d_c) \times d_s}$를 얻기 위해 $z_t$와 concat된다.

또한 음악 신호의 글로벌한 정보를 모델링하는 self-attention block에 조건부 표현을 도입한다. Self-attention block에서 \(z'_t \in \mathbb{R}^{(d_t + d_c) \times d_s}\)의 중간 표현이 \(\phi (z'_t) \in \mathbb{R}^{d_a \times d_\phi}\)이고 \(S \in \mathbb{R}^{n \times d_E}\)인 경우 출력은 다음과 같이 계산된다.

\[\begin{equation} \textrm{Attention} (Q, K, V) = \textrm{softmax} (\frac{QK^\top}{\sqrt{d_k}}) V \\ \textrm{head}_i = \textrm{Attention} (Q_i, K_i, V_i) \\ Q_i = \phi (z'_t) \cdot W_i^Q \\ K_i = \textrm{Concat} (\phi (z'_t) \cdot W_i^K, S \cdot W_i^{SK}) \\ V_i = \textrm{Concat} (\phi (z'_t) \cdot W_i^V, S \cdot W_i^{SV}) \\ \textrm{CSA} (\phi (z'_t), S) = \textrm{Concat} (\textrm{head}_1, \cdots, \textrm{head}_h) W^O \end{equation}\]

여기서 $W_i^Q \in \mathbb{R}^{d_\phi \times d_q}$, $W_i^K \in \mathbb{R}^{d_\phi \times d_k}$, $W_i^V \in \mathbb{R}^{d_\phi \times d_v}$, $W_i^{SK} \in \mathbb{R}^{d_E \times d_k}$, $W_i^{SV} \in \mathbb{R}^{d_E \times d_v}$, $W^O \in \mathbb{R}^{hd_v \times d_\phi}$는 파라미터 행렬이고, $h$는 head의 수이다. $\textrm{CSA}(\cdot, \cdot)$은 conditional self-attention 연산이다.

Training

Progressive distillation 논문을 따라 더 안정적인 denoising process를 위해 가중치 함수를 “SNR+1” weighting으로 설정한다.

구체적으로, noise schedule $\alpha_t$와 $\sigma_t$에 대하여 cosine schedule $\alpha_t = \cos (\pi t / 2)$, $\sigma_t = \sin (\pi t / 2)$를 채택하고 variance-preserving diffusion process는 $\alpha_t^2 + \sigma_t^2 = 1$을 만족한다.

함수 근사를 \(\hat{v}_\theta (z_t, t, y)\)로 표시한다. 여기서 $y$는 조건을 나타낸다. \(\hat{v}_\theta (z_t, t, y)\)의 예측 목표는 velocity $v_t = \alpha_t - \sigma_t x$이며 \(\hat{x} = \alpha_t z_t - \sigma_t \hat{v}_\theta (z_t, t, y)\)를 얻을 수 있다. 목적 함수는 다음과 같다.

\[\begin{aligned} L_\theta &= (1 + \alpha_t^2 / \sigma_t^2) \| x - \hat{x}_t \|_2^2 \\ &= \| v_t - \hat{v}_t \|_2^2 \end{aligned}\]

Algorithm 1은 progressive distillation 논문이 제안한 diffusion 목적 함수로 전체 학습 과정을 보여준다.

Experiments

1. Dataset

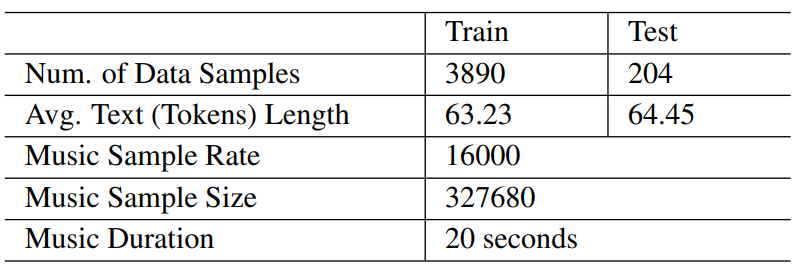
다음은 저자들이 수집하여 데이터셋으로 사용한 웹 음악과 텍스트에 대한 통계이다.

다음은 수집한 데이터셋의 예시들이다.

2. Results

다음은 텍스트-음악 관련성을 비교한 표이다. Score는 1, 2, 3으로 세 모델의 순위를 매긴 것이다.

다음은 음악 품질을 비교한 표이다. Score는 1~5로 인간이 평가한 것이다.

Analysis

Diversity

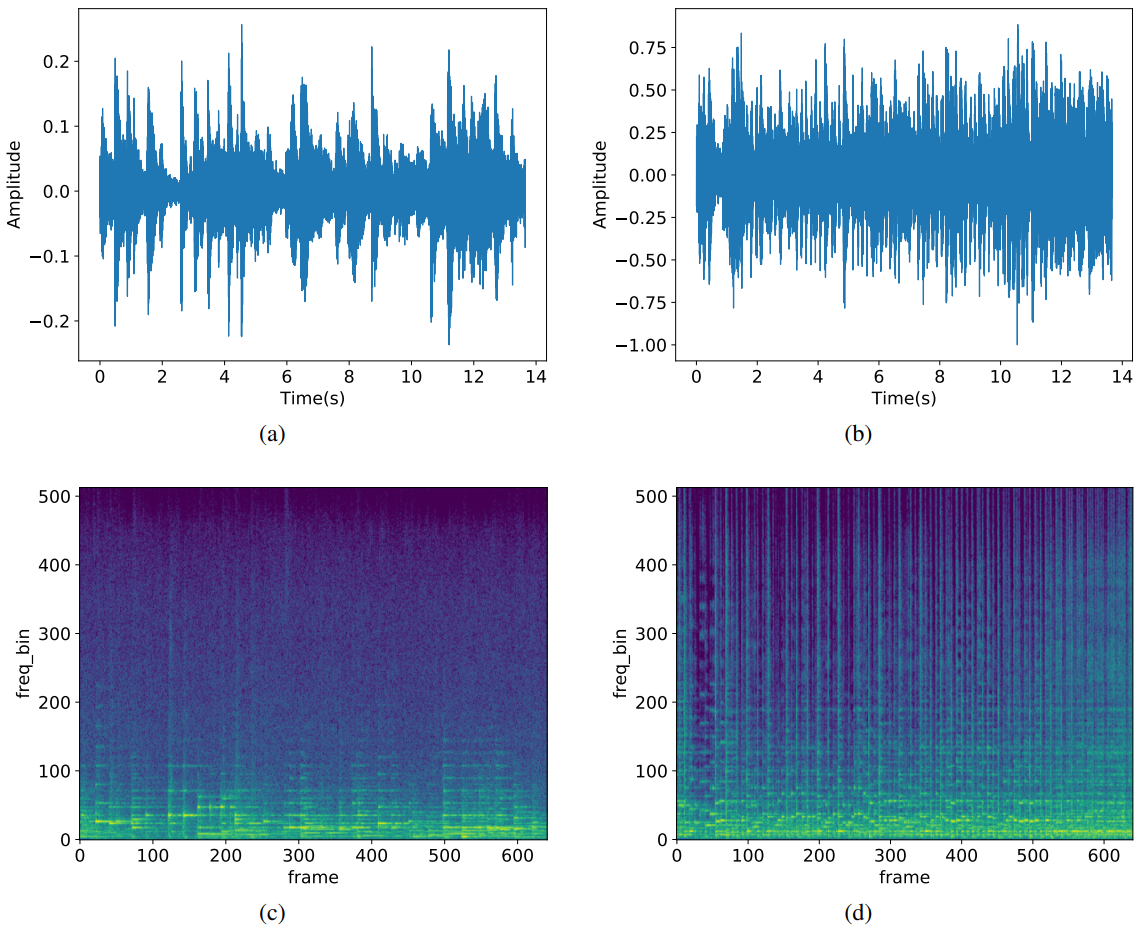
다음은 생성된 음악 샘플의 spectrogram과 waveform이다. (a)와 (c)의 텍스트는 “The piano piece is light and comfortable yet deeply affectionate”이고 (b)와 (d)의 텍스트는 “A passionate, fast-paced guitar piece”이다.

Comparison of Different Text Condition Fusing Operations

다음은 fuse 연산의 선택에 따른 테스트 셋에 대한 MSE이다.

Music Tag Conditioning

다음은 자유 형식 텍스트와 해당 음악 태그의 예시이다.

다음은 채택된 태그와 폐기된 태그의 예시이다.

다음은 두 가지 컨디셔닝 텍스트 포맷 간의 텍스트-음악 관련성을 비교한 표이다.