[논문리뷰] Progressive Distillation for Fast Sampling of Diffusion Models
ICLR 2022. [Paper]
Tim Salimans | Jonathan Ho
Google Research, Brain Team
1 Feb 2022
Introduction
Diffusion model의 주요 단점은 샘플링 속도이다. 강력한 컨디셔닝 설정(TTS, 이미지 super-resolution)이나 보조 classifier를 사용하여 샘플러를 guide하는 경우와 같이 샘플링이 비교적 적은 step으로 수행될 수 있는 경우에는 상황이 크게 다르다. 그러나 적은 컨디셔닝 정보가 사용 가능한 경우에서는 샘플링이 다소 어렵다. 이러한 설정의 예로는 unconditional한 이미지 생성 및 표준 클래스 조건부 이미지 생성이 있으며, 현재 다른 유형의 생성 모델의 캐싱 최적화에 적합하지 않은 네트워크 평가를 사용하여 수백 또는 수천 step을 필요로 한다.
본 논문에서는 이전 연구들에서 가장 느린 설정을 나타내는 unconditional 및 클래스 조건부 이미지 생성에서 diffusion model의 샘플링 시간을 수십 배 줄인다. 사전 학습된 diffusion model에 대한 $N$-step DDIM sampler의 동작을 샘플 품질의 저하가 거의 없는 $N/2$ step의 새 모델로 증류하는 절차를 제시한다. Progressive Distillation라고 하는 이 distillation 절차를 반복하여 4 step으로 생성되는 모델을 생성하며, 여전히 수천 step을 사용하는 최신 모델과 경쟁력 있는 샘플 품질을 유지한다.
Background on Diffusion Models
본 논문에서는 continuous time에서의 diffusion model을 고려한다. 학습 데이터는 $x \sim p(x)$로 나타낸다. Diffusion model은 latent 변수 \(z = \{z_t \vert t \in [0, 1]\}\)을 가지며, $\lambda_t = \log (\alpha_t^2 / \sigma_t^2)$인 $\alpha_t$, $\sigma_t$로 구성된 noise schedule에 의해 지정된다. $\lambda_t$는 SNR(신호 대 잡음 비)이며 $t$에 따라 단조 감소한다.
Forward process $q(z \vert x)$는 다음과 같은 Markovian 구조를 만족하는 Gaussian process이다.
\[\begin{aligned} q(z_t \vert x) &= \mathcal{N}(z_t; \alpha_t x, \sigma_t^2 I) \\ q(z_t \vert z_s) &= \mathcal{N}(z_t; (\alpha_t / \alpha_s) z_s, \sigma_{t \vert s}^2 I) \end{aligned}\]여기서 $0 \le s < t \le 1$이고 $\sigma_{t \vert s}^2 = (1 - e^{\lambda_t - \lambda_s}) \sigma_t^2$이다.
Diffusion model의 역할은 $z_t \sim q(z_t \vert x)$를 \(\hat{x}_\theta (z_t) \approx x\)로 denoise하는 것이다. 이 denoising model \(\hat{x}_\theta\)를 가중 MSE loss를 사용하여 학습시킨다.
\[\begin{equation} \mathbb{E}_{\epsilon, t} [w(\lambda_t) \| \hat{x}_\theta (z_t) - x \|_2^2] \end{equation}\]학습된 모델에서의 샘플링은 여러 방법으로 수행할 수 있다. 가장 간단한 방법은 discrete time ancestral sampling이다. 이 샘플러를 정의하기 위해 forward process를 다음과 같이 역으로 설명할 수 있다.
\[\begin{aligned} q(z_s \vert z_t, x) &= \mathcal{N}(z_s; \tilde{\mu}_{s \vert t} (z_t, x), \tilde{\sigma}_{s \vert t}^2 I) \\ \tilde{\mu}_{s \vert t} (z_t, x) &= e^{\lambda_t - \lambda_s} (\alpha_s / \alpha_t) z_t + (1 - e^{\lambda_t - \lambda_s}) \alpha_s x \\ \tilde{\sigma}_{s \vert t}^2 &= (1 - e^{\lambda_t - \lambda_s}) \sigma_s^2 \end{aligned}\]이 정의를 사용하여 ancestral sampler를 정의할 수 있다. $z_1 \sim \mathcal{N}(0,I)$에서 시작하여 다음 규칙을 따른다.
\[\begin{aligned} z_s &= \tilde{\mu}_{s \vert t} (z_t, \hat{x}_\theta (z_t)) + \sqrt{(\tilde{\sigma}_{s \vert t}^2)^{1-\gamma} (\sigma_{t \vert s}^2)^\gamma} \epsilon \\ &= e^{\lambda_t - \lambda_s} (\alpha_s / \alpha_t) z_t + (1 - e^{\lambda_t - \lambda_s}) \alpha_s \hat{x}_\theta (z_t) + \sqrt{(\tilde{\sigma}_{s \vert t}^2)^{1-\gamma} (\sigma_{t \vert s}^2)^\gamma} \epsilon \end{aligned}\]여기서 $\epsilon$은 Gaussian noise이고 $\gamma$는 샘플링 중에 얼마나 noise를 추가할 지를 제어하는 hyperparameter이다.
Score-based generative modeling through stochastic differential equation 논문에서는 probability flow ODE
\[\begin{equation} dz_t = [f (z_t, t) - \frac{1}{2} g^2 (t) \nabla_z \log \hat{p}_\theta (z_t)] dt \\ \textrm{where} \quad \nabla_z \log \hat{p}_\theta (z_t) = \frac{\alpha_t \hat{x}_\theta (z_t) - z_t}{\sigma_t^2} \end{equation}\]를 풀어 denoising model $\hat{x}_\theta (z_t)$가 noise $z_1$을 샘플 $x$에 deterministic하게 매핑할 수 있음을 보였다.
본 논문은 Variational Diffusion Model 논문을 따라
\[\begin{equation} f(z_t, t) = \frac{d \log \alpha_t}{dt} z_t \\ g^2 (t) = \frac{d \sigma_t^2}{dt} - 2 \frac{d \log \alpha_t}{dt} \sigma_t^2 \end{equation}\]을 사용한다. \(\hat{x}_\theta (z_t)\)가 신경망으로 parameterize되므로 이 방정식은 neural ODE의 특별한 케이스이며, continuous normalizing flow라고 부른다.
위의 방정식의 ODE는 Euler rule이나 Runge-Kutta method와 같은 방법으로 수치적으로 풀 수 있다. DDIM 샘플러는 이 ODE를 위한 integration rule로 이해할 수 있다. DDIM의 업데이트 규칙은 다음과 같다.
\[\begin{aligned} z_s &= \alpha_s \hat{x}_\theta (z_t) + \sigma_s \frac{z_t - \alpha_t \hat{x}_\theta (z_t)}{\alpha_t} \\ &= e^{(\lambda_t - \lambda_s)/2} (\alpha_s / \alpha_t) z_t + (1-e^{(\lambda_t - \lambda_s)/2}) \alpha_s \hat{x}_\theta (z_t) \end{aligned}\]\(\hat{x}_\theta (z_t)\)가 약간의 smoothness 조건을 충족하는 경우 probability flow ODE의 수치 적분에 의해 도입된 오차는 적분 step의 수가 무한대로 커짐에 따라 사라진다. 이는 실제로 수치 적분의 정확도와 모델에서 생성된 샘플의 품질 및 이러한 샘플을 생성하는 데 필요한 시간 사이의 trade-off로 이어진다. 지금까지의 연구에 있는 대부분의 모델은 최고 품질의 샘플을 생성하기 위해 수백 또는 수천 개의 통합 step이 필요했으며, 이는 생성 모델링의 많은 애플리케이션에서 사용할 수 없다. 따라서 여기서는 정확하지만 느린 ODE integrator를 여전히 매우 정확한 훨씬 더 빠른 모델로 증류하는 방법을 제안한다. 이 아이디어는 아래 그림에 시각화되어 있다.
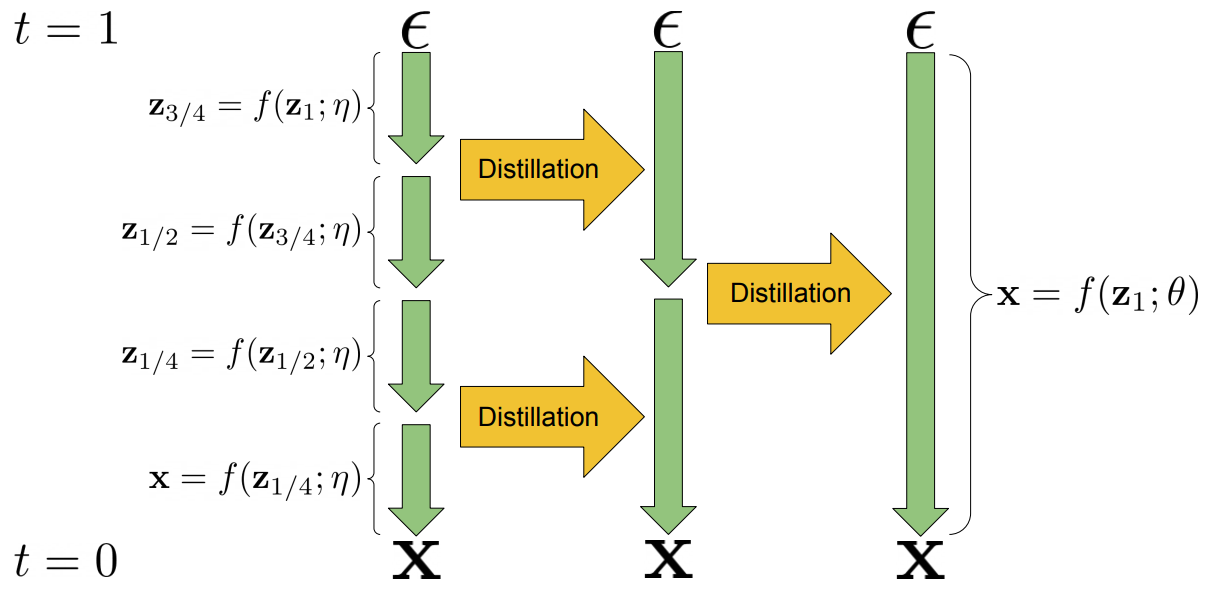
Progressive Distillation
샘플링 시간에 diffusion model을 보다 효율적으로 만들기 위해 느린 teacher diffusion model을 더 빠른 student model로 증류하여 필요한 샘플링 step 수를 반복적으로 절반으로 줄이는 알고리즘인 progressive distillation을 제안한다. Progressive distillation의 구현은 원래 diffusion model을 학습하기 위한 구현과 매우 유사하다. Algorithm 1과 Algorithm 2는 progressive distillation의 상대적 변화를 녹색으로 강조 표시한 diffusion model 학습과 progressive distillation을 나란히 제시한다.

표준 방식으로 학습하여 얻은 teacher diffusion model을 사용하여 progressive distillation 절차를 시작한다. Progressive distillation을 반복할 때마다 동일한 파라미터와 동일한 모델 정의를 모두 사용하여 teacher의 복사본으로 student model을 초기화한다. 표준 학습에서와 같이 학습 데이터셋에서 데이터를 샘플링하고 noise를 추가한 다음 이 noisy한 데이터 $z_t$에 student denoising model을 적용하여 학습 loss를 형성한다.
Progressive distillation의 주요 차이점은 denoising model의 목적 함수를 설정하는 방법에 있다. 원래 데이터 $x$ 대신 student DDIM step 1개가 teacher DDIM step 2개와 일치하도록 만드는 타겟 $\tilde{x}$를 향한 student model denoise가 있다. $z_t$에서 시작하여 $z_{t−1/N}$에서 끝나는 teacher를 사용하여 2개의 DDIM 샘플링 step을 실행하여 이 타겟 값을 계산한다. 여기서 $N$은 student 샘플링 step의 수이다. DDIM의 step 1개를 반전시켜 단일 step에서 $z_t$에서 $z_{t-1/N}$으로 이동하기 위해 student model이 예측해야 하는 값을 계산한다. 결과 타겟 값 $\tilde{x} (z_t)$는 주어진 teacher model과 시작점 $z_t$에 따라 완전히 결정되며, 이를 통해 student model은 $z_t$에서 평가될 때 예리한 예측을 할 수 있다. 대조적으로, 원래 데이터 포인트 $x$는 주어진 $z_t$에서 완전히 결정되지 않는다. 이것은 원래의 denoising model이 가능한 $x$ 값의 가중 평균을 예측하여 흐릿한 예측을 생성한다는 것을 의미한다. 더 예리한 예측을 통해 학생 모델은 샘플링을 더 빠르게 진행할 수 있다.
$N$개의 샘플링 step을 통해 student model을 학습하기 위해 distillation을 실행한 후 $N/2$ step으로 절차를 반복할 수 있다. 그러면 student model이 새 teacher가 되고 새 student model이 이 모델의 복사본을 만들어 초기화된다.
원래 모델을 학습하는 절차와 달리 항상 discrete time에 progressive distillation을 실행한다. 이 discrete time을 샘플링하여 가장 높은 시간 인덱스가 0의 SNR, 즉 $\alpha_1 = 0$에 해당하도록 샘플링한다. 저자들은 이것이 0이 아닌 SNR에서 시작하는 것보다 약간 더 잘 작동한다는 것을 발견했다. 원본 모델을 학습하고 progressive distillation를 수행할 때 모두 사용한다.
Diffusion Model Parameterization and Training Loss
$\sigma_t^2 = 1 − \alpha_t^2$인 표준 variance-preserving diffusion process를 가정하며, 이는 variance-exploding과 같은 다른 diffusion process에서도 동등하게 고려될 수 있다. Cosine schedule $\alpha_t = \cos (0.5 \pi t)$를 사용한다.
DDPM과 다른 연구의 대부분은 암시적으로
\[\begin{equation} \hat{x}_\theta (z_t) = \frac{1}{\alpha_t} (z_t − \sigma_t \hat{\epsilon}_\theta (z_t)) \end{equation}\]를 설정하는 신경망 \(\hat{\epsilon}_\theta (z_t)\)를 사용한 $\epsilon$의 직접 예측을 통해 denoising model을 reparameterize하도록 선택한다. 이 경우 학습 loss는 일반적으로 $\epsilon$-space의 MSE로 정의된다.
\[\begin{equation} L_\theta = \| \epsilon - \hat{\epsilon}_\theta (z_t) \|_2^2 = \bigg\| \frac{1}{\sigma_t} (z_t - \alpha_t x) - \frac{1}{\sigma_t} (z_t - \alpha_t \hat{x}_\theta (z_t)) \bigg\|_2^2 = \frac{\alpha_t^2}{\sigma_t^2} \| x - \hat{x}_\theta (z_t) \|_2^2 \end{equation}\]이는 log-SNR $\lambda_t = \log [\alpha_t^2 / \sigma_t^2]$에 대해 가중치 함수가 $w(\lambda_t) = \exp(\lambda_t)$로 제공되는 $x$-space에서 가중 재구성 loss로 동등하게 볼 수 있다.
이 표준 사양은 원래 모델을 학습하는 데 적합하지만 distillation에는 적합하지 않다. 원래 diffusion model을 학습하고 progressive distillation을 시작할 때 모델이 광범위한 SNR $\alpha_t^2 / \sigma_t^2$에서 평가되지만, distillation이 진행됨에 따라 점점 더 낮아지는 SNR에서 평가하게 된다. SNR이 0이 되면 신경망 출력 \(\hat{\epsilon}_\theta (z_t)\)의 작은 변화가 $x$-space의 암시적 예측에 미치는 영향은 점점 더 증폭된다. 이는 \(\hat{x}_\theta (z_t) = \frac{1}{\alpha_t} (z_t - \sigma_t \hat{\epsilon}_\theta (z_t))\)가 $\alpha_t \rightarrow 0$으로 나누기 때문이다. 초기 실수의 영향은 반복적인 $z_t$의 클리핑에 의해 제한되고 이후 업데이트는 모든 실수를 수정할 수 있기 때문에 많은 step을 수행할 때 큰 문제가 되지 않지만, 샘플링 step의 수를 줄이면 점점 더 중요해진다. 결국 단일 샘플링 step까지 증류하면 모델에 대한 입력은 순수한 noise만 되며 이는 SNR이 0, 즉 $\alpha_t = 0, \sigma_t = 1$에 해당한다. 극단적인 경우 $\epsilon$-예측과 $x$-예측 사이의 연결이 완전히 끊어진다. 관찰된 데이터 $z_t = \epsilon$은 더 이상 $x$에 대해 정보를 제공하지 않으며 예측 \(\hat{\epsilon}_\theta (z_t)\)는 더 이상 암시적으로 $x$를 예측하지 않는다. 가중치 함수 $w(\lambda_t)$가 이 SNR에서 재구성 loss에 0의 가중치를 부여하게 된다.
따라서 distillation이 작동하려면 암시적 예측 \(\hat{x}_\theta (z_t)\)가 $\lambda_t = \log[\alpha_t^2 / \sigma_t^2]$가 변함에 따라 안정적으로 유지되는 방식으로 diffusion model을 parameterize해야 한다. 저자들은 다음 옵션들을 시도했고 모두 progressive distillation과 잘 작동한다는 것을 알았다.
- $x$를 직접 예측
- $x$와 $\epsilon$을 서로 다른 출력 채널로 모두 예측한 다음 \(\hat{x} = \sigma_t^2 \tilde{x}_\theta (z_t) + \alpha_t (z_t - \sigma_t \tilde{\epsilon}_\theta (z_t))\)로 예측을 합쳐 $x$와 $\epsilon$을 부드럽게 보간
- $v = \alpha_t \epsilon = \sigma_t x$를 예측한 다음 \(\hat{x} = \alpha_t z_t - \sigma_t \hat{v}_\theta (z_t)\)를 사용
적절한 parameterization을 결정하는 것 외에도 재구성 loss의 가중치 $w(\lambda_t)$를 결정해야 한다. DDPM 설정은 SNR로 재구성 loss에 가중치를 부여하고 SNR이 0인 데이터에 암시적으로 0의 가중치를 부여하므로 distillation에 적합한 선택이 아니다. 다음과 같은 두 가지 대체 가중치를 고려한다.
- ‘Truncated SNR’ weighting:
- ‘SNR + 1’ weighting:
실제로, loss 가중치 선택은 학습 중에 $\alpha_t$, $\sigma_t$가 샘플링되는 방식도 고려해야 한다. 이 샘플링 분포는 예상 loss가 각 SNR에 부여하는 가중치를 강력하게 결정하기 때문이다. 아래 그림은 cosine schedule의 효과를 포함하거나 제외하여 결과적인 loss 가중치를 시각화한 것이다.
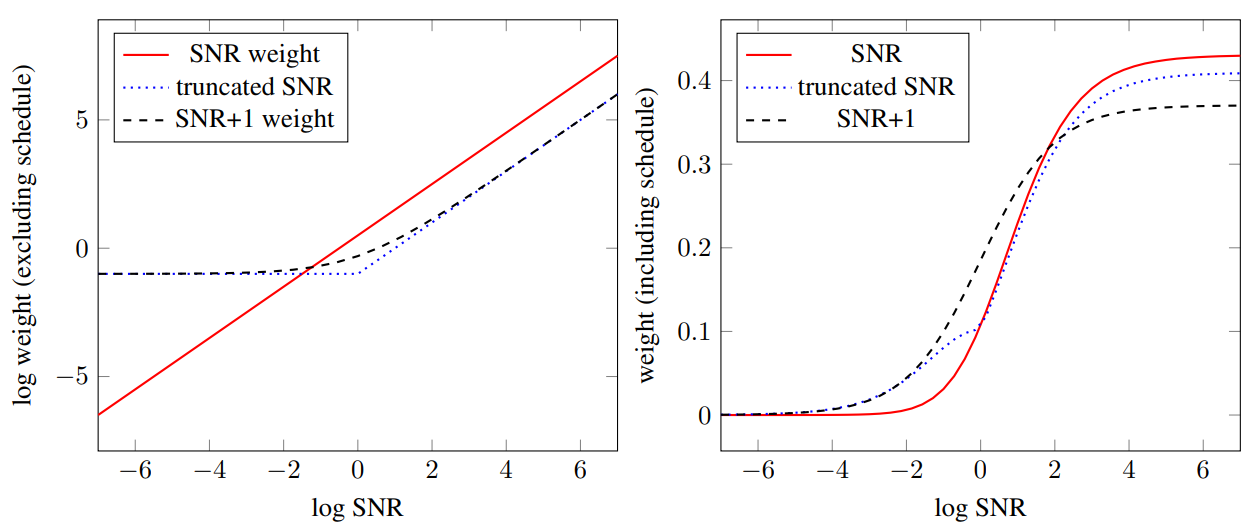
Experiments
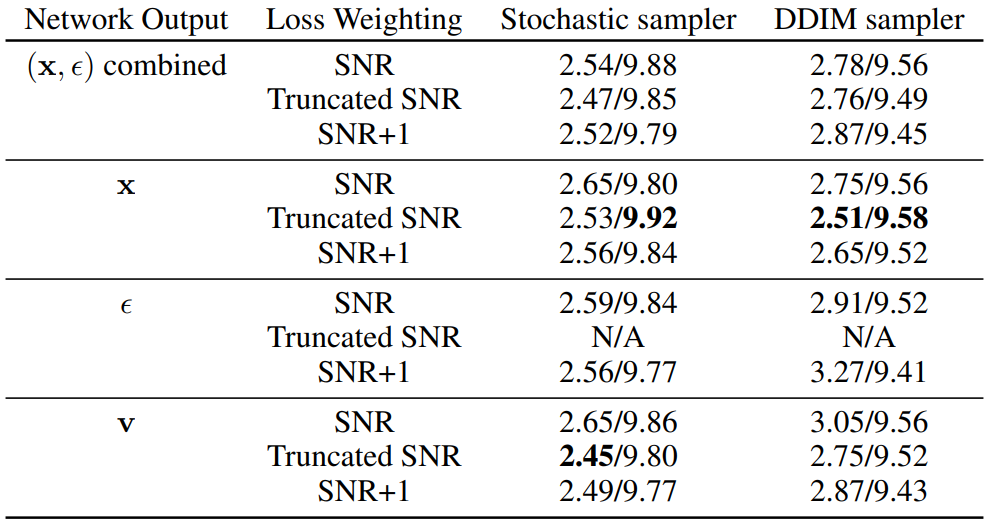
1. Model parameterization and training loss
다음은 unconditional CIFAR-10에 대한 샘플 품질을 측정한 표이다. (FID / IS)
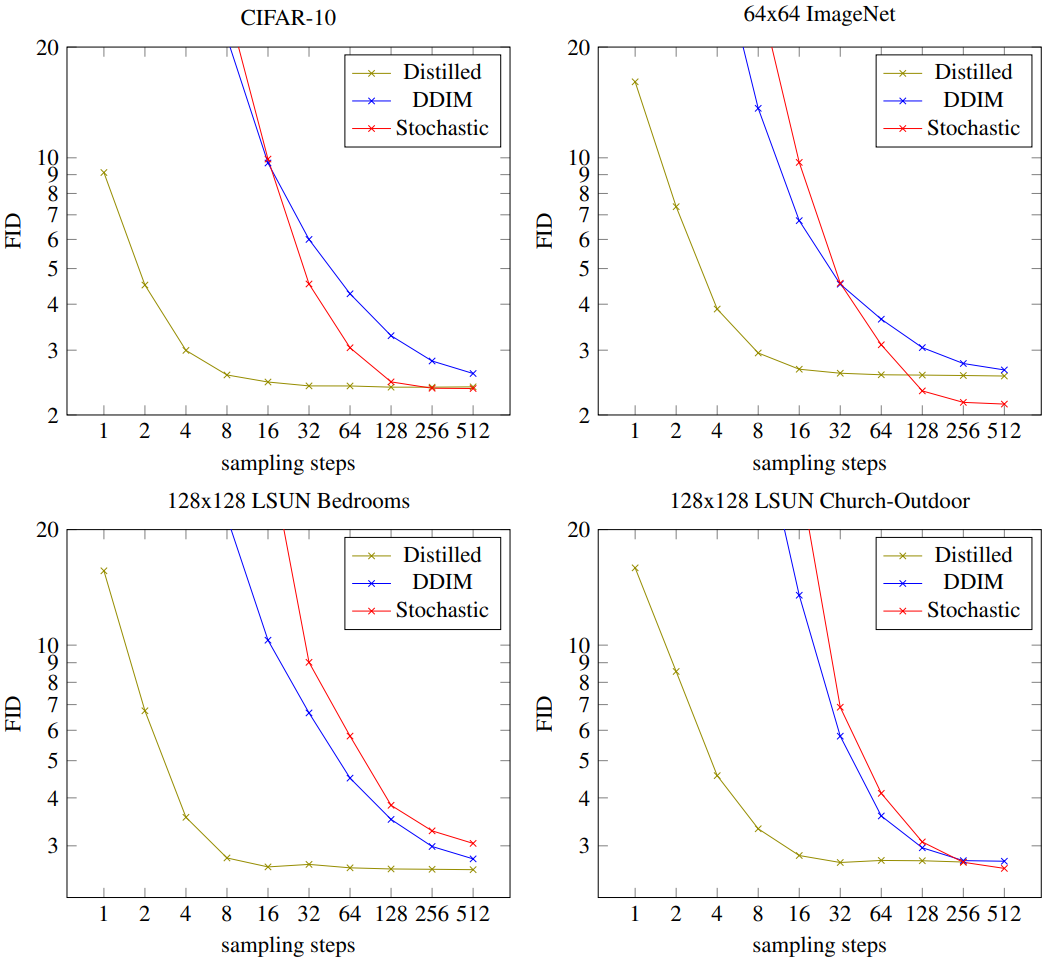
2. Progressive distillation
다음은 다양한 데이터셋에 대하여 샘플링 step에 따른 FID를 나타낸 그래프이다.
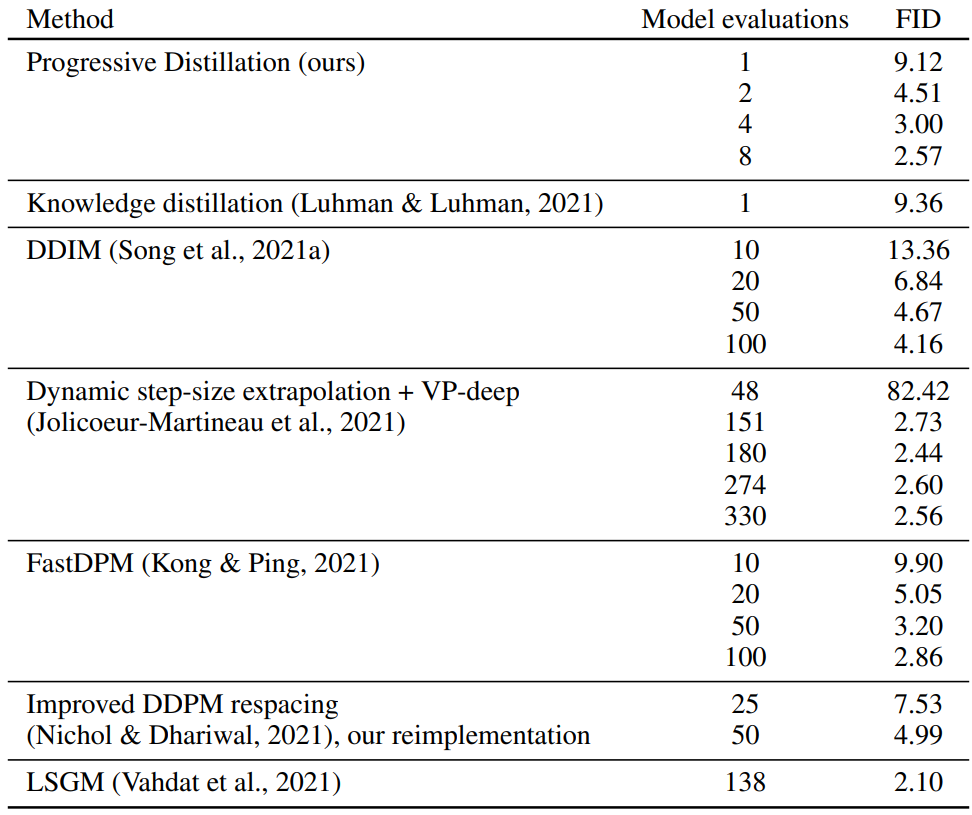
다음은 CIFAR-10에서 다양한 diffusion model과 빠른 샘플링 결과를 비교한 표이다.
다음은 다양한 샘플링 step의 distilled 64$\times$64 ImageNet model의 랜덤한 샘플들이다. (클래스는 malamute, random seed 고정)
