[논문리뷰] Deep Unsupervised Learning using Nonequilibrium Thermodynamics
ICML 2015. [Paper] [Github]
Jascha Sohl-Dickstein, Eric A. Weiss, Niru Maheswaranathan, Surya Ganguli
Stanford University | University of California, Berkeley
12 Mar 2015
Introduction
생성 모델은 tractability와 flexibility 사이에서 trade-off가 있다. Tractable한 모델은 가우시안 분포처럼 수치적으로 계산이 되며 데이터에 쉽게 맞출 수 있다. 하지만, 이러한 모델은 복잡한 데이터셋을 적절하게 설명하기 어렵다. 반대로, flexible한 모델은 임의의 데이터에 대해서도 적절하게 설명할 수 있지만 학습하고 평가하고 샘플을 생성하는데 일반적으로 매우 복잡한 Monte Carlo process가 필요하다.
저자는 다음 4가지가 가능한 probabilistic model을 정의하는 새로운 방법을 제안한다.
- 굉장히 유연한 모델 구조
- 정확한 샘플링
- 사후 계산 등을 위해 다른 분포들과의 쉬운 곱셈
- Model log likelihood와 각 state의 확률 계산이 쉽다
저자는 diffusion process를 사용하여 가우시안 분포처럼 잘 알려진 분포에서 목표로 하는 데이터의 분포로 점진적으로 변환하는 generative Marcov chain을 사용한다. Marcov chain이기 때문에 각 상태는 이전 상태에 대해 독립적이다. Diffusion chain의 각 step의 확률을 수치적으로 계산할 수 있으므로 전체 chain도 수치적으로 계산할 수 있다.
확산 과정에 대한 작은 변화를 추정하는 것이 학습 과정에 포함된다. 이는 수치적으로 정규화할 수 없는 하나의 potential function을 사용하여 전체 분포를 설명하는 것보다 작은 변화를 추정하는 것이 더 tractable하기 때문이다. 또한 임의의 데이터 분포에 대해서 diffusion process가 존재하기 때문에 이 방법은 임의의 형태의 데이터 분포를 표현할 수 있다.
Algorithm
논문의 목표는 어떤 복잡한 데이터 분포라도 간단하고 tractable한 분포로 변환하는 forward diffusion process를 정의하고, 이에 대한 유한시간 (finite-time) 역변환 process를 학습하다. 이 역변환 process는 간단한 분포를 목표 데이터 분포로 변환하기 때문에 목표로 하는 생성적 모델이라고 할 수 있다. 또한 논문에서는 역변환 process의 entropy bound를 유도하고 어떻게 학습된 분포가 다른 분포와 곱해질 수 있는 지 보여준다.
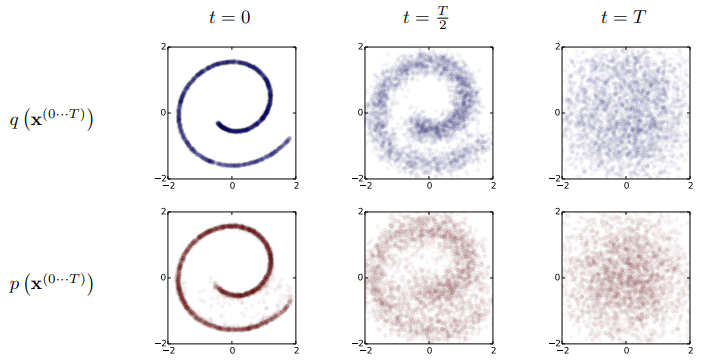
1. Forward Trajectory
데이터 분포를 $q(x^{(0)})$, tractable한 간단한 분포를 $\pi(y)$, $\pi(y)$에 대한 Markov diffusion kernel을 $T_\pi (y | y’)$, diffusion rate를 $\beta$라 하면 다음과 같다.
\[\begin{equation} \pi(y) = \int dy' T_\pi (y | y'; \beta) \pi(y') \\ q(x^{(t)} | x^{(t-1)}) = T_\pi (x^{(t)} | x^{(t-1)} ; \beta _t) \end{equation}\]
데이터 분포 $q(x^{(0)})$에서 $T$ 단계로 diffusion을 수행한다고 하면 다음과 같다.
$q(x^{(t)}|x^{(t-1)})$은 같은 분산을 갖는 가우시안 분포거나 독립적인 이항 분포다.
2. Reverse Trajectory
Reverse trajectory는 forward trajectory와 같은 trajectory지만 반대로 진행되도록 학습된다.
\[\begin{equation} p(x^{(T)}) = \pi (x^{(T)}) \\ p(x^{(0 \cdots T)}) = p(x^{(T)}) \prod_{t=1}^T p(x^{(t-1)} | x^{(t)}) \end{equation}\]연속적인 확산을 위해서는 reverse가 forward와 같은 함수 형태로 되어야 한다. $q(x^{(t)}|x^{(t-1)})$가 가우시안 분포이고 $\beta_t$가 작으면 $q(x^{(t-1)}|x^{(t)})$도 가우시안 분포이다. Trajectory가 길수록 diffusion rate $\beta$가 작아질 수 있다.
학습 과정에서 가우시안 분포 kernel의 평균과 분산만 예측하면 된다. 이 알고리즘의 computational cost는 평균과 분산의 함수의 cost와 time-step의 개수의 곱이다. 논문의 모든 실험에서 이 함수들은 MLP이다.
3. Model Probability
데이터 분포에 대한 생성 모델의 확률은
\[\begin{equation} p(x^{(0)}) = \int dx^{(1 \cdots T)} p(x^{(0 \cdots T)}) \end{equation}\]이다. 이 적분식은 tractable하지 않다. 그러므로 대신 forward에 대해 평균을 낸 forward와 reverse의 상대적 확률을 계산한다. (Annealed importance sampling과 Jarzynski 등식에서 힌트를 얻었다고 함)
\[\begin{aligned} p(x^{(0)}) &= \int dx^{(1 \cdots T)} p(x^{(0 \cdots T)}) \frac{q(x^{(1 \cdots T)} | x^{(0)})}{q(x^{(1 \cdots T)} | x^{(0)})} \\ &= \int dx^{(1 \cdots T)} q(x^{(1 \cdots T)} | x^{(0)}) \frac{p(x^{(0 \cdots T)})}{q(x^{(1 \cdots T)} | x^{(0)})} \\ &= \int dx^{(1 \cdots T)} q(x^{(1 \cdots T)} | x^{(0)}) p(x^{(T)}) \prod_{t=1}^T \frac{p(x^{(t-1)}|x^{(t)})}{q(x^{(t)} | x^{(t-1)})} \end{aligned}\]4. Training
학습은 model log likelihood를 최대화하는 방향으로 진행된다.
\[\begin{aligned} L &= \int dx^{(0)} q(x^{(0)}) \log p(x^{(0)}) \\ &= \int dx^{(0)} q(x^{(0)}) \log \bigg[ \int dx^{(1 \cdots T)} q(x^{(1 \cdots T)} | x^{(0)}) p(x^{(T)}) \prod_{t=1}^T \frac{p(x^{(t-1)}|x^{(t)})}{q(x^{(t)} | x^{(t-1)})} \bigg] \end{aligned}\]Jensen 부등식에 의해 $L$은 lower bound를 가진다.
\[\begin{aligned} L &\ge \int dx^{(0 \cdots T)} q(x^{(0 \cdots T)}) \log \bigg[ p(x^{(T)}) \prod_{t=1}^T \frac{p(x^{(t-1)}|x^{(t)})}{q(x^{(t)} | x^{(t-1)})} \bigg] = K \end{aligned}\]Appendix에 의해 $K$는 다음과 같이 KL divergence와 엔트로피들로 표현할 수 있다.
\[\begin{aligned} L \ge K =& -\sum_{t=2}^T \int dx^{(0)} dx^{(t)} q(x^{(0)}, x^{(t)}) D_{KL} \bigg( q(x^{(t-1)} | x^{(t)}, x^{(0)}) \; || \; p(x^{(t-1)} | x^{(t)}) \bigg) \\ &+ H_q (X^{(T)} | X^{(0)}) - H_q (X^{(1)} | X^{(0)}) - H_p (X^{(T)}) \end{aligned}\]엔트로피들과 KL divergence는 계산이 가능하므로 $K$는 계산이 가능하다. 등호는 forward와 reverse가 같을 때 성립하므로 $\beta_t$가 충분히 작으면 $L$이 $K$와 거의 같다고 볼 수 있다.
Reverse Markov transition을 찾는 학습은 lower bound를 최대화하는 것과 같다.
\[\begin{aligned} \hat{p} (x^{(t-1)} | x^{(t)}) = \underset{p(x^{(t-1)} | x^{(t)})}{\operatorname{argmax}} K \end{aligned}\]$\beta_t$를 어떻게 선택하는 지가 모델의 성능에 중요하다. 가우시안 분포의 경우 $\beta_{2 \cdots T}$는 $K$에 대한 gradient ascent로 구하였으며 $\beta_1$은 overfitting을 막기 위해 고정된 값을 사용하였다고 한다.
5. Multiplying Distributions, and Computing Posteriors
모델의 분포 $p(x^{(0)})$와 다른 분포 $r(x^{(0)})$을 곱하여 새로운 분포 $\tilde{p}(x^{(0)}) \propto p(x^{(0)}) r(x^{(0)})$을 만든다고 하자. $\tilde{p}(x^{(0)})$를 구하기 위해서 $t$에서의 각 분포 $p(x^{(t)})$와 $r(x^{(t)})$를 곱하여 $\tilde{p}(x^{(t)})$를 구하고, $\tilde{p}(x^{(0 \cdots T)})$를 수정된 reverse trajectory라고 생각하자. $\tilde{p}$도 확률 분포이기 때문에 normalizaing constant $\tilde{Z}_t$를 이용하여 정의할 수 있다.
\[\begin{equation} \tilde{p} (x^{(t)}) = \frac{1}{\tilde{Z}_t} p(x^{(t)}) r(x^{(t)}) \end{equation}\]
Reverse diffusion process의 Markov kernel $p(x^{(t)} | x^{(t+1)})$은 다음 식을 따른다.
Pertubed Markov kernel $\tilde{p}(x^{(t)} | x^{(t+1)})$도 위 식을 따른다고 하면 다음과 같다.
따라서 다음 식이 성립한다.
\[\begin{equation} \tilde{p} (x^{(t)} | x^{(t+1)}) = p (x^{(t)} | x^{(t+1)}) \frac{\tilde{Z}_{t+1} r(x^{(t)})}{\tilde{Z}_t r(x^{(t+1)})} \end{equation}\]위 식이 정규화된 확률 분포가 아닐 수 있기 때문에 다음과 같이 정의한다.
\[\begin{equation} \tilde{p} (x^{(t)} | x^{(t+1)}) = \frac{1}{\tilde{Z}_t (x^{(t+1)})} p (x^{(t)} | x^{(t+1)}) r(x^{(t)}) \end{equation}\]
가우시안 분포의 경우, 각각의 diffusion step이 작은 분산에 의해 $r(x^{(t)})$에서 peak를 가진다고 한다. 이는 $\frac{r(x^{(t)})}{r(x^{(t+1)})}$을 $p(x^{(t)} | x^{(t+1)})$에 대한 작은 pertubation으로 생각할 수 있다는 뜻이다. 가우시안 분포에 대한 작은 pertubation은 평균에 영향을 주지만 normalization 상수에는 영향을 주지 않기 때문에 위 식과 같이 정의할 수 있다.
만약 $r(x^{(t)})$가 충분히 부드럽다면 이는 reverse diffusion kernel $p(x^{(t)}|x^{(t+1)})$에 대한 작은 pertubation으로 생각할 수 있고, 이 때 $\tilde{p}$는 $p$와 같은 형태이다. 만약 $r(x^{(t)})$가 가우시안 분포와 closed form으로 곱할 수 있다면 $r(x^{(t)})$는 $p(x^{(t)}|x^{(t+1)})$에 closed from으로 곱할 수 있다.
$r(x^{(t)})$는 trajectory를 따라 천천히 변하는 함수로 골라야 하며 실험에서는 상수로 두었다.
Forward를 알고 있기 때문에 reverse에서 각 step의 조건부 엔트로피에 대한 upper bound와 lower bound를 구할 수 있으므로 log likelihood에 대해 구할 수 있다.
\[\begin{equation} H_q (X^{(t)}|X^{(t-1)}) + H_q (X^{(t-1)}|X^{(0)}) - H_q (X^{(t)}|X^{(0)}) \le H_q (X^{(t-1) }|X^{(t)}) \le H_q (X^{(t)}|X^{(t-1)}) \end{equation}\]
Upper bound와 lower bound는 $q(x^{(1 \cdots T)}|x^{(0)})$에만 의존하므로 계산할 수 있다.
Experiments
- Dataset: Toy data, MNIST, CIFAR10, Dead Leaf Images, Bark Texture Images
- 각 데이터셋에 대한 생성 및 impainting
Forward diffusion kernel과 reverse diffusion kernel은 다음과 같다.
\[\begin{equation} q(x^{(t)}|x^{(t-1)}) = \mathcal{N} (x^{(t)}; x^{(t-1)} \sqrt{1-\beta_t}, I \beta_t) \\ p(x^{(t-1)}|x^{(t)}) = \mathcal{N} (x^{(t-1)}; f_\mu (x^{(t)}, t), f_\Sigma (x^{(t)}, t)) \end{equation}\]$f_\mu$와 $f_\Sigma$는 MLP이고 $f_\mu$, $f_\Sigma$, $\beta_{1 \cdots T}$를 학습 대상이다.
Results
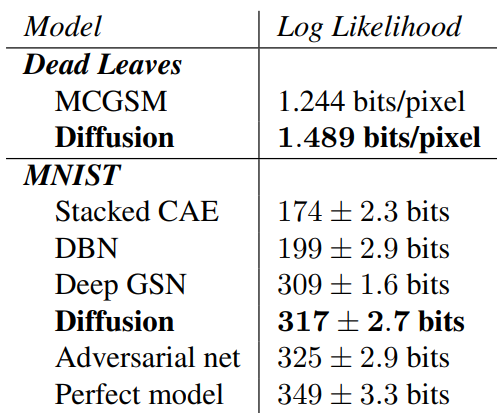

원본과는 조금 다르지만 상당히 괜찮은 결과가 나타났다.