[논문리뷰] Denoising Diffusion Probabilistic Models (DDPM)
NeurIPS 2020. [Paper] [Github]
Jonathan Ho, Ajay Jain, Pieter Abbeel
UC Berkeley
19 Jun 2020
Introduction
이 논문은 diffusion model(리뷰)을 발전시킨 논문이다. Diffusion model은 parameterized Markov chain을 학습시켜 유한 시간 후에 원하는 데이터에 맞는 샘플을 만드는 모델이다. Forward process에서는 Markov chain이 점진적으로 noise를 추가하여 최종적으로 가우시안 noise로 만든다. 반대로 reverse process는 가우시안 noise로부터 점진적으로 noise를 제거하여 최종적으로 원하는 데이터에 맞는 샘플을 만든다. Diffusion이 작은 양의 가우시안 noise로 구성되어 있기 때문에 샘플링 chain을 조건부 가우시안으로 설정하는 것으로 충분하고, 간단한 신경먕으로 parameterize할 수 있다.
기존 diffusion model은 정의하기 쉽고 훈련하기 효율적이지만 고품질의 샘플을 만들지 못하였다. 반면, DDPM은 고품질의 샘플을 만들 수 있을 뿐만 아니라 다른 생성 모델 (ex. GAN)보다 더 우수한 결과를 보였다. 또한, diffusion model의 특정 parameterization이 훈련 중 여러 noise 레벨에서의 denoising score matching과 비슷하며, 샘플링 중 Langevin dynamics 문제를 푸는 것과 동등하다는 것을 보였다.
그 밖의 특징으로는
- DDPM은 고품질의 샘플을 생성하지만 다른 likelihood 기반의 모델보다 경쟁력 있는 log likelihood가 없다.
- DDPM의 lossless codelength가 대부분 인지할 수 없는 이미지 세부 정보를 설명하는 데 사용되었다.
- Diffusion model의 샘플링이 autoregressive model의 디코딩과 유사한 점진적 디코딩이라는 것을 보였다.
Diffusion model

Diffusion model은 $p_\theta (x_0) := \int p_\theta (x_{0:T}) dx_{1:T}$로 정의한다. $x_1, \cdots, x_T$는 데이터 $x_0 \sim q(x_0 )$와 같은 크기이다. Joint distribution (결합 분포) $p_\theta (x_{0:T})$는 reverse process라 불리며, $p(x_T ) = \mathcal{N} (x_T ; 0, I )$에서 시작하는 Gaussian transition으로 이루어진 Markov chain으로 정의된다.
\[\begin{equation} p_\theta (x_{0:T}) := p(x_T) \prod_{t=1}^T p_\theta (x_{t-1}|x_{t}) \\ p_\theta (x_{t-1}|x_{t}) := \mathcal{N} (x_{t-1} ; \mu_\theta (x_t , t), \Sigma_\theta (x_t , t)) \end{equation}\]
Diffusion model이 다른 latent variable model과 다른 점은 forward process 혹은 diffusion process라 불리는 approximate posterior $q(x_{1:T}|x_0)$가
$\beta_1, \cdots, \beta_T$에 따라 가우시안 noise를 점진적으로 추가하는 Markov chain이라는 것이다.
학습은 negative log likelihood에 대한 일반적인 variational bound을 최적화하는 것으로 진행된다.
\[\begin{equation} L:= \mathbb{E} [-\log p_\theta (x_0)] \le \mathbb{E}_q \bigg[ -\log \frac{p_\theta (x_{0:T})}{q(x_{1:T}|x_0)} \bigg] \le \mathbb{E}_q \bigg[ -\log p(x_T) - \sum_{t \ge 1} \log \frac{p_\theta (x_{t-1}|x_t)}{q(x_t|x_{t-1})} \bigg] \end{equation}\]$\beta_t$는 reparameterization으로 학습하거나 hyper-parameter로 상수로 둘 수 있다. 또한 $\beta_t$가 충분히 작으면 forward process와 reverse process가 같은 함수 형태이므로 reverse process의 표현력은 $p_\theta (x_{t-1}|x_t)$에서 가우시안 conditional의 선택에 따라 부분적으로 보장된다.
Forward process에서 주목할만한 것은 closed form으로 임의의 시간 $t$에서 샘플링 $x_t$가 가능하다는 것이다.
\[\begin{equation} \alpha_t := 1-\beta_t, \quad \bar{\alpha_t} := \prod_{s=1}^t \alpha_s \\ q(x_t | x_0) = \mathcal{N} (x_t ; \sqrt{\vphantom{1} \bar{\alpha_t}} x_0 , (1-\bar{\alpha_t})I) \end{equation}\]증명)
$q (x_{t}|x_{t-1}) = \mathcal{N} (x_{t} ; \sqrt{1-\beta_t} x_{t-1}, \beta_t I)$이므로 $$ \begin{aligned} x_t &= \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1} & (\epsilon_{t-1} \sim \mathcal{N} (0, I)) \\ &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1-\alpha_t} \epsilon_{t-1} \\ &= \sqrt{\alpha_t} (\sqrt{\alpha_{t-1}} x_{t-2} + \sqrt{1-\alpha_{t-1}} \epsilon_{t-2}) + \sqrt{1-\alpha_t} \epsilon_{t-1} & (\epsilon_{t-2} \sim \mathcal{N}(0, I))\\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t (1-\alpha_{t-1})} \epsilon_{t-2} + \sqrt{1-\alpha_t} \epsilon_{t-1} \\ \end{aligned} $$ $\alpha_t (1-\alpha_{t-1}) + 1-\alpha_t = 1 - \alpha_t \alpha_{t-1}$이므로 $\sqrt{\alpha_t (1-\alpha_{t-1})} \epsilon_{t-2} + \sqrt{1-\alpha_t} \epsilon_{t-1} \sim \mathcal{N}(0, (1 - \alpha_t \alpha_{t-1})I)$이고 대입하면, $$ \begin{aligned} x_t &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \epsilon'_{t-2} & (\epsilon'_{t-2} \sim \mathcal{N}(0, I)) \\ &= \sqrt{\alpha_t \alpha_{t-1} \alpha_{t-2}} x_{t-3} + \sqrt{1 - \alpha_t \alpha_{t-1} \alpha_{t-2}} \epsilon'_{t-3} & (\epsilon'_{t-3} \sim \mathcal{N}(0, I)) \\ &= \cdots \\ &= \sqrt{ \vphantom{1} \bar{\alpha}_t} x_{0} + \sqrt{1 - \bar{\alpha}_t} \epsilon'_{0} & (\epsilon'_{0} \sim \mathcal{N}(0, I)) \end{aligned} $$
따라서, $q(x_t | x_0) = \mathcal{N} (x_t ; \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 , (1-\bar{\alpha}_t)I)$이다.
한 번에 샘플링이 가능하므로 stochastic gradient descent을 이용하여 효율적인 학습이 가능하다. $L$을 다음과 같이 다시 쓰면 분산 감소로 인해 추가 개선이 가능하다.
위 식은 KL divergence으로 forward process posterior (ground truth)와 $p_\theta (x_{t-1} \vert x_t)$를 직접 비교하며, 이는 tractable하다. 두 가우시안 분포에 대한 KL Divergence는 closed form으로 된 Rao-Blackwellized 방식으로 계산할 수 있기 때문에 $L$을 쉽게 계산할 수 있다.
$q(x_{t-1} \vert x_t, x_0)$는 다음 식으로 계산할 수 있다.
\[\begin{aligned} q (x_{t-1} | x_t, x_0) &= \mathcal{N} (x_{t-1} ; \tilde{\mu_t} (x_t, x_0), \tilde{\beta_t} I), \\ \rm{where} \quad \tilde{\mu_t} (x_t, x_0) &:= \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} x_t \quad \rm{and} \quad \tilde{\beta_t} := \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t \end{aligned}\]증명)
$$ \begin{aligned} q(x_{t-1} | x_t, x_0) &= q(x_t | x_{t-1}, x_0) \frac{q(x_{t-1} | x_0)}{q(x_t | x_0)} \\ & \propto \exp \bigg(- \frac{1}{2} (\frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} x_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\vphantom{1} \bar{\alpha}_{t}} x_0)^2}{1-\bar{\alpha}_{t}}) \bigg) \\ &= \exp \bigg(- \frac{1}{2} (\frac{x_t^2 - 2\sqrt{\alpha_t} x_t x_{t-1} + \alpha_t x_{t-1}^2}{\beta_t} + \frac{x_{t-1}^2 - 2\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} x_{t-1} x_0 + \bar{\alpha}_{t-1} x_0^2}{1-\bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\vphantom{1} \bar{\alpha}_{t}} x_0)^2}{1-\bar{\alpha}_{t}}) \bigg) \\ &= \exp \bigg(- \frac{1}{2} ((\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}}) x_{t-1}^2 - 2(\frac{\sqrt{\alpha_t}}{\beta_t}x_t + \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_0) x_{t-1} + C(x_t, x_0)) \bigg) \\ &= A(x_t, x_0) \exp \bigg( -\frac{1}{2 \tilde{\beta}_t} (x_{t-1} - \tilde{\mu}_t (x_t, x_0))^2 \bigg) \\ \tilde{\beta}_t &= 1 / \bigg( \frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}} \bigg) = \frac{\beta_t (1-\bar{\alpha}_{t-1})}{\alpha_t (1-\bar{\alpha}_{t-1}) + \beta_t} = \frac{\beta_t (1-\bar{\alpha}_{t-1})}{\alpha_t -\alpha_t \bar{\alpha}_{t-1} + \beta_t} = \frac{1-\bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \\ \tilde{\mu_t} (x_t, x_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t}x_t + \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_0) \tilde{\beta}_t = (\frac{\sqrt{\alpha_t}}{\beta_t}x_t + \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_0) \frac{1-\bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \\ &= \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} x_t \end{aligned} $$
위와 같이 $q(x_{t-1} \vert x_t)$는 계산하기 어렵지만 $q(x_{t-1} \vert x_t, x_0)$는 쉽게 계산할 수 있다. 즉, $x_t$에서 $x_{t-1}$을 바로 구하는 것은 어렵지만 $x_0$를 조건으로 주면 쉽게 구할 수 있다.
Diffusion models and denoising autoencoders
1. Forward process와 $L_T$
실험에서 forward process의 분산 $\beta_t$을 상수로 고정할 것이기 때문에 approximate posterior $q$에는 학습되는 파라미터가 없다. 따라서 학습 중에 $L_T$는 상수이므로 무시할 수 있다.
2. Reverse process와 $L_{1:T-1}$
$1 < t \le T$에 대한 $p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (x_{t-1} ; \mu_\theta (x_t, t) ; \Sigma_\theta (x_t, t))$을 다음과 같이 설정하였다.
- $\Sigma_\theta (x_t, t) = \sigma_t^2 I$로 두었으며, $\sigma_t$는 학습하지 않는 $t$에 의존하는 상수이다. 실험을 해 본 결과, $\sigma_t^2 = \beta_t$나 $\sigma_t^2 = \tilde{\beta_t}$로 두어도 비슷한 결과가 나온다고 한다.
- $\mu_\theta (x_t, t)$를 나타내기 위해 특정 parameterization을 제안한다. $p_\theta (x_{t-1}\vert x_t) = \mathcal{N} (x_{t-1} ; \mu_\theta (x_t, t), \sigma_t^2 I)$에 대하여 다음과 같이 쓸 수 있다.
증명)
$q(x) = \mathcal{N} (\mu_1, \sigma_1^2 I)$이고 $p(x) = \mathcal{N} (\mu_2, \sigma_2^2 I)$이라고 하자 ($\mu_1, \mu_2 \in \mathbb{R}^d$). $x \in \mathbb{R}^d$일 때, KL divergence는 다음과 같다. $$ \begin{equation} D_{KL} (q \| p) = - \int q(x) \log p(x) dx + \int q(x) \log q(x) dx \end{equation} $$ $$ \begin{aligned} - \int q(x) \log p(x) dx &= - \int q(x) \log \frac{1}{(\sqrt{2\pi} \sigma_2)^{d}} \exp \bigg(- \frac{(x-\mu_2)^2}{2\sigma_2^2}\bigg) dx \\ &= \frac{d}{2} \log (2\pi \sigma_2^2) - \int q(x) \bigg( - \frac{(x-\mu_2)^2}{2\sigma_2^2} \bigg) dx \\ &= \frac{d}{2} \log (2\pi \sigma_2^2) + \frac{\mathbb{E}_q [(x - \mu_2)^\top (x - \mu_2)]}{2\sigma_2^2} \\ &= \frac{d}{2} \log (2\pi \sigma_2^2) + \frac{\mathbb{E}_q [x^\top x] - 2 \mathbb{E}_q [x^\top \mu_2] + \mathbb{E}_q [\mu_2^\top \mu_2]}{2\sigma_2^2} \\ &= \frac{d}{2} \log (2\pi \sigma_2^2) + \frac{\textrm{tr}(\sigma_1^2 I) + \mu_1^\top \mu_1 - 2 \mu_2^\top \mathbb{E}_q [x] + \mu_2^\top \mu_2}{2\sigma_2^2} \\ &= \frac{d}{2} \log (2\pi \sigma_2^2) + \frac{d \sigma_1^2 + \mu_1^\top \mu_1 - 2 \mu_2^\top \mu_1 + \mu_2^\top \mu_2}{2\sigma_2^2} \\ &= \frac{d}{2} \log (2\pi \sigma_2^2) + \frac{d \sigma_1^2 + \| \mu_1 - \mu_2 \|^2}{2\sigma_2^2} \end{aligned} $$ $$ \begin{aligned} D_{KL} (q \| p) &= \frac{d}{2} \log (2\pi \sigma_2^2) + \frac{d \sigma_1^2 + \| \mu_1 - \mu_2 \|^2}{2\sigma_2^2} - \frac{d}{2} \log (2\pi \sigma_1^2) - \frac{d}{2} \\ &= \frac{d}{2} \log ( \frac{\sigma_2^2}{\sigma_1^2}) + \frac{d(\sigma_1^2 - \sigma_2^2) + \| \mu_1 - \mu_2 \|^2}{2\sigma_2^2} \end{aligned} $$ $q (x_{t-1} \vert x_t, x_0) = \mathcal{N} (x_{t-1} ; \tilde{\mu_t} (x_t, x_0), \tilde{\beta_t} I)$이고 $p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (x_{t-1} ; \mu_\theta (x_t, t), \sigma_t^2 I)$이므로 $\mu_1 = \tilde{\mu_t} (x_t, x_0)$, $\mu_2 = \mu_\theta (x_t, t)$, $\sigma_1^2 = \tilde{\beta_t}$, $\sigma_2^2 = \sigma_t^2$를 $L_{t-1}$에 대입하면 다음과 같다. $$ \begin{aligned} L_{t-1} &= \mathbb{E}_q \bigg[ D_{KL} (q(x_{t-1} | x_t , x_0) \; || \; p_\theta (x_{t-1} | x_t)) \bigg] \\ &= \mathbb{E}_q \bigg[ \frac{d}{2} \log ( \frac{\sigma_t^2}{\tilde{\beta_t}}) + \frac{d (\tilde{\beta_t} - \sigma_t^2) + (\tilde{\mu_t} (x_t, x_0) - \mu_\theta (x_t, t))^2}{2\sigma_t^2} \bigg]\\ &= \mathbb{E}_q \bigg[ \frac{1}{2\sigma_t^2} \| \tilde{\mu_t} (x_t, x_0) - \mu_\theta (x_t, t) \|^2 \bigg] + \mathbb{E}_q \bigg[ \frac{d}{2} \log ( \frac{\sigma_t^2}{\tilde{\beta_t}}) + \frac{d (\tilde{\beta_t} - \sigma_t^2)}{2\sigma_t^2}\bigg] \\ &= \mathbb{E}_q \bigg[ \frac{1}{2\sigma_t^2} \| \tilde{\mu_t} (x_t, x_0) - \mu_\theta (x_t, t) \|^2 \bigg] + C \end{aligned} $$ $C$는 $\tilde{\beta_t}$와 $\sigma_t^2$으로 계산되는 값이므로 $t$에만 의존하는 값이다.
$C$는 $\theta$에 독립적인 상수이다. 따라서 $L_{t-1}$은 ground truth $\tilde{\mu_t}$에 $\mu_\theta$가 가까워지도록 학습된다. 샘플링하는 식
을 변형하면
\[\begin{equation} x_0 = \frac{1}{\sqrt{\vphantom{1} \bar{\alpha}_t}} (x_t(x_0, \epsilon) - \sqrt{1-\bar{\alpha}_t}\epsilon) \end{equation}\]이고 $\tilde{\mu_t} (x_t, x_0)$에 대입하여 정리하면 다음과 같다.
\[\begin{aligned} \tilde{\mu_t} (x_t, x_0) &= \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} x_t \\ &= \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\vphantom{1} \bar{\alpha}_t}} (x_t(x_0, \epsilon) - \sqrt{1-\bar{\alpha}_t}\epsilon) + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} x_t \\ &= \bigg( \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}}}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \frac{\beta_t}{1-\bar{\alpha}_t} + \frac{1}{\sqrt{\alpha_t}} \frac{\alpha_t(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} \bigg) x_t(x_0, \epsilon) - \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}}}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon\\ &= \frac{1}{\sqrt{\alpha_t}} \bigg(\bigg( \frac{\beta_t + \alpha_t - \alpha_t \bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \bigg) x_t(x_0, \epsilon) - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon \bigg) \\ &= \frac{1}{\sqrt{\alpha_t}} \bigg( x_t(x_0, \epsilon) - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon \bigg) \\ L_{t-1} - C &= \mathbb{E}_{x_0, \epsilon} \bigg[ \frac{1}{2\sigma_t^2} \bigg\| \frac{1}{\sqrt{\alpha_t}} \bigg( x_t(x_0, \epsilon) - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon \bigg) - \mu_\theta (x_t(x_0, \epsilon), t) \bigg\|^2 \bigg] \end{aligned}\]$\mu_\theta$에서 $x_t$는 forward process에서 만들어 모델의 입력으로 줄 수 있다. 따라서 다음과 같이 parameterization을 하면 마치 residual을 계산하는 것처럼 $x_{t-1}$을 바로 계산하는 것이 아니라 제거된 noise $\epsilon$을 예측하여 $x_t$에서 빼주는 방식을 사용할 수 있다.
\[\begin{equation} \mu_\theta (x_t, t) = \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta (x_t, t) \bigg) \end{equation}\]$\epsilon_\theta$는 $x_t$로부터 $\epsilon$을 예측하는 function approximator이다.
$x_{t-1} \sim p_\theta (x_{t-1} \vert x_t)$의 샘플링은 다음과 같이 진행된다.
\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{\beta_t}{\sqrt{1- \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \bigg) + \sigma_t z, \quad z \sim \mathcal{N} (0, I) \end{equation}\]정리하면, 학습과 샘플링 과정은 다음 알고리즘과 같이 진행된다.

샘플링 과정 (Algorithm 2)은 데이터 밀도의 학습된 기울기로 $\epsilon_\theta$를 사용하는 Langevin 역학과 유사하다.
추가로, parameterization을 한 $\mu_\theta$를 objective function 식에 대입하면
\[\begin{equation} L_{t-1} - C = \mathbb{E}_{x_0, \epsilon} \bigg[ \frac{\beta_t^2}{2\sigma_t^2 \alpha_t (1-\bar{\alpha}_t)} \| \epsilon - \epsilon_\theta (\sqrt{\vphantom{1} \bar{\alpha}_t} + \sqrt{1-\bar{\alpha}_t} \epsilon, t) \|^2 \bigg] \end{equation}\]인데, 이는 여러 noise 레벨에서의 denoising score matching과 유사하며 Langevin-like reverse process의 variational bound과 같다.
3. Data scaling, reverse process decoder, and $L_0$
이미지 데이터는 0부터 255까지의 정수로 되어있고 -1부터 1까지의 실수로 선형적으로 스케일링되어 주어진다. 이를 통해 신경망(reverse process)이 표준 정규 prior $p(x_T)$에서 시작하여 언제나 스케일링된 이미지로 갈 수 있게 한다. 이산적인(discrete) log likelihood를 얻기 위하여 reverse process의 마지막 항 $L_0$를 가우시안 분포 $\mathcal{N} (x_0; \mu_\theta (x_1, 1), \sigma_1^2 I)$에서 나온 독립적인 discrete decoder로 설정하였다.
\[\begin{aligned} p_\theta (x_0 | x_1) &= \prod_{i=1}^D \int_{\delta_{-} (x_0^i)}^{\delta_{+} (x_0^i)} \mathcal{N} (x; \mu_\theta^i (x_1, 1), \sigma_1^2) dx \\ \delta_{+} (x) &= \begin{cases} \infty & (x = 1) \\ x + \frac{1}{255} & (x < 1) \end{cases} \quad &\delta_{-} (x) = \begin{cases} -\infty & (x = -1) \\ x - \frac{1}{255} & (x > -1) \end{cases} \end{aligned}\]$D$는 데이터의 dimensionality이며 $i$는 각 좌표를 나타낸다.
4. Simplified training objective
저자들은 training objective를 다음과 같이 simplification하였다.
\[\begin{equation} L_{\rm{simple}} := \mathbb{E}_{t, x_0, \epsilon} \bigg[ \| \epsilon - \epsilon_\theta (\sqrt{\vphantom{1} \bar{\alpha}_t} + \sqrt{1-\bar{\alpha}_t} \epsilon, t) \|^2 \bigg] \end{equation}\]여기서 $t$는 1과 T 사이에서 uniform하다. Simplified objective는 기존의 training objective에서 가중치를 제거한 형태이다. 이 가중치항은 $t$에 대한 함수로, $t$가 작을수록 큰 값을 가지기 때문에 $t$가 작을 때 더 큰 가중치가 부여되어 학습된다. 즉, 매우 작은 양의 noise가 있는 데이터에서 noise를 제거하는데 집중되어 학습된다. 따라서 매우 작은 $t$에서는 학습이 잘 진행되지만 큰 $t$에서는 학습이 잘 되지 않기 때문에 가중치항을 제거하여 큰 $t$에서도 학습이 잘 진행되도록 한다.
실험을 통하여 가중치항을 제거한 $L_{\rm{simple}}$이 더 좋은 샘플을 생성하는 것을 확인했다고 한다.
Experiments
- 모든 실험에서 $T = 1000$
- $\beta_t$는 $\beta_1 = 10^{-4}$에서 $\beta_T = 0.02$로 선형적으로 증가
- $x_T$에서 signal-to-noise-ratio는 최대한 작게 $(L_T = D_{KL}(q(x_T\vert x_0) \; | \; \mathcal{N}(0,I)) \approx 10^{-5})$
- 신경망은 group normalization을 사용하는 U-Net backbone (unmasked PixelCNN++과 비슷한 구조)
- Transformer sinusoidal position embedding으로 모델에게 시간 $t$를 입력
- 16x16 feature map에서 self-attention 사용
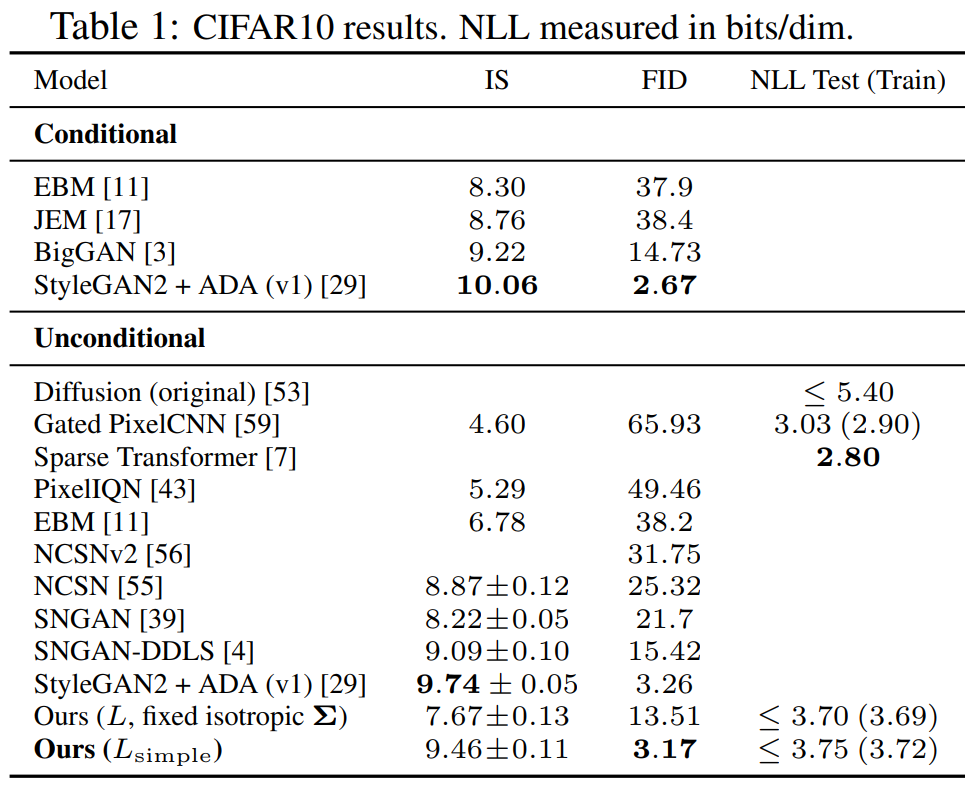
Results