[논문리뷰] Consistency Models

ICML 2023. [Paper] [Github]
Yang Song, Prafulla Dhariwal, Mark Chen, Ilya Sutskever
OpenAI
2 Mar 2023

Introduction

Score 기반 생성 모델이라고도 하는 diffusion model은 이미지 생성, 오디오 합성, 동영상 생성을 포함한 여러 분야에서 전례 없는 성공을 거두었다. Diffusion model의 핵심 능력은 랜덤 초기 벡터에서 noise를 점진적으로 제거하는 반복 샘플링 프로세스이다. 이 반복 프로세스는 더 많은 반복을 위해 추가 컴퓨팅을 사용하면 일반적으로 더 나은 품질의 샘플을 생성하므로 컴퓨팅과 샘플 품질의 유연한 균형을 제공한다. 또한 diffusion model의 많은 zero-shot 데이터 편집 능력의 핵심으로, 이미지 인페인팅, colorization, stroke-guided 이미지 편집에서 컴퓨터 단층 촬영과 자기 공명 영상에 이르기까지 까다로운 inverse problem을 해결할 수 있다. 그러나 GAN, VAE, normalizing flow와 같은 단일 step 생성 모델과 비교할 때 diffusion model의 반복 생성 절차는 일반적으로 샘플 생성을 위해 10~2000배 더 많은 컴퓨팅이 필요하므로 inference가 느리고 실시간 애플리케이션이 제한된다.

본 논문의 목표는 필요할 때 샘플 품질을 위해 컴퓨팅을 거래하고 zero-shot 데이터 편집 작업을 수행하는 것과 같은 반복 샘플링의 중요한 이점을 희생하지 않고 효율적인 단일 step 생성을 촉진하는 생성 모델을 만드는 것이다.

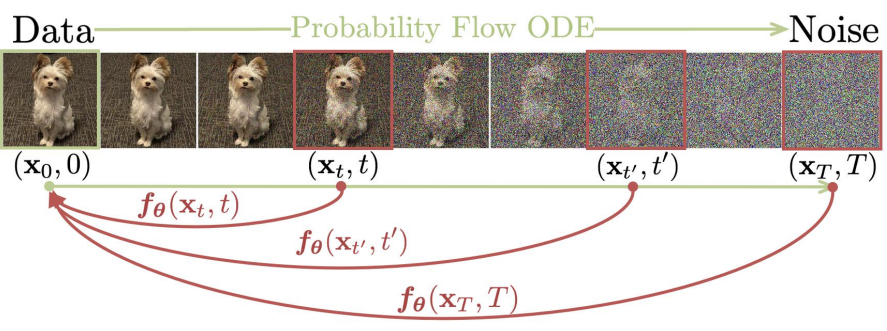
위 그림에서 볼 수 있듯이 연속 시간 diffusion model의 확률 흐름 상미분 방정식 (PF ODE) 위에 구축한다. 이 모델의 궤적은 데이터 분포를 다루기 쉬운 noise 분포로 부드럽게 전환한다. 궤적의 시작점에 임의의 timestep에서 임의의 지점을 매핑하는 모델을 학습할 것을 제안한다. 본 논문의 모델의 주목할만한 속성은 self-consistency이다. 즉, 동일한 궤적에 있는 지점이 동일한 초기 지점에 매핑된다. 따라서 이러한 모델을 consistency model이라고 한다. Consistency model을 사용하면 단 한 번의 네트워크 평가로 랜덤 noise 벡터 (ODE 궤적의 끝점, $x_T$)를 변환하여 데이터 샘플 (ODE 궤적의 초기 지점, $x_0$)을 생성할 수 있다. 중요한 것은 여러 timestep에서 consistency model의 출력을 연결함으로써 샘플 품질을 개선하고 더 많은 컴퓨팅 비용으로 zero-shot 데이터 편집을 수행할 수 있다는 것이다.

본 논문은 consistency model을 학습시키기 위해 self-consistency 속성을 적용하는 두 가지 방법을 제공한다. 첫 번째 방법은 numerical ODE solver와 사전 학습된 diffusion model을 사용하여 PF ODE 궤적에서 인접한 포인트 쌍을 생성한다. 이러한 쌍에 대한 모델 출력 간의 차이를 최소화함으로써 diffusion model을 consistency model로 효과적으로 추출하여 한 번의 네트워크 평가로 고품질 샘플을 생성할 수 있다. 대조적으로, 두 번째 방법은 사전 학습된 diffusion model에 대한 필요성을 완전히 제거하여 consistency model을 독립적으로 학습할 수 있게 한다. 이 접근 방식은 consistency model을 생성 모델의 독립적인 계열로 만든다. 중요한 것은 두 접근 방식 모두 적대적 학습을 필요로 하지 않으며 둘 다 아키텍처에 약간의 제약을 가하여 consistency model을 parameterize하기 위해 유연한 신경망을 사용할 수 있다는 것이다.

Diffusion Models

Consistency model은 연속 시간 diffusion model 이론에서 크게 영감을 받았다. Diffusion model은 가우시안 섭동을 통해 데이터를 noise로 점진적으로 섭동한 다음 순차적 denoising step을 통해 noise에서 샘플을 생성하여 데이터를 생성한다. $p_\textrm{data} (x)$를 데이터 분포라 하자. Diffusion model은 확률적 미분 방정식 (SDE)을 사용하여 $p_\textrm{data} (x)$를 diffuse하는 것으로 시작한다.

\[\begin{equation} dx_t = \mu (x_t, t) dt + \sigma (t) dw_t \end{equation}\]

여기서 $t \in [0, T]$는 고정 상수이고 $\mu$와 $\sigma$는 각각 drift 계수와 diffusion 계수이다. \(\{w_t\}_{t \in [0,T]}\)는 표준 브라운 운동이다. $x_t$의 분포를 $p_t (x)$라 하면 결과적으로 $p_0 (x) = p_\textrm{data} (x)$가 된다. 이 SDE의 주목할 만한 특성은 Probability Flow (PF) ODE라고 하는 상미분 방정식의 존재이다. 이 방정식의 $t$에서 샘플링된 솔루션 궤적은 $p_\textrm{data} (x)$에 따라 분포된다.

\[\begin{equation} dx_t = \bigg[ \mu (x_t, t) - \frac{1}{2} \sigma(t)^2 \nabla \log p_t (x_t) \bigg] dt \end{equation}\]

여기서 $\nabla \log p_t (x)$는 $p_t (x)$의 score function이다. 따라서 diffusion model은 score 기반 생성 모델이라고도 한다.

일반적으로 SDE는 $p_T (x)$가 다루기 쉬운 가우시안 분포 $\pi (x)$에 가깝도록 설계된다. 저자들은 $\mu(x, t) = 0$, $\sigma(t) = \sqrt{2t}$인 EDM의 설정을 채택하였다. 이 경우 $p_t (x) = p_\textrm{data}(x) \otimes \mathcal{N} (0, t^2 I)$가 되며, 여기서 $\otimes$는 convolution 연산을 나타내고 $\pi (x) = \mathcal{N} (0, T^2 I)$이다. 샘플링을 위해 먼저 score matching을 통해 score model $s_\phi (x, t) \approx \nabla \log p_t (x)$를 학습한 위 식에 연결하여 PF ODE의 경험적 추정치를 얻는다.

\[\begin{equation} \frac{dx_t}{dt} = - t s_\phi (x_t, t) \end{equation}\]

위 식을 경험적 PF ODE라고 한다. 다음으로 \(\hat{x}_T \sim \pi = \mathcal{N} (0, T^2 I)\)를 샘플링하여 경험적 PF ODE를 초기화하고 Euler solver나 Heun solver와 같은 numerical ODE solver를 사용하여 역방향으로 풀어 솔루션 궤적 \(\{\hat{x}_t\}_{t \in [0, T]}\)를 얻는다. \(\hat{x}_0\)는 데이터 분포 $p_\textrm{data} (x)$에서의 대략적인 샘플로 볼 수 있다. 수치적 불안정성을 피하기 위해 일반적으로 $t = \epsilon$에서 solver를 중지한다. 여기서 $\epsilon$는 고정된 작은 양수이고 \(\hat{x}_\epsilon\)를 근사 샘플로 간주한다. EDM을 따라 이미지 픽셀 값을 $[-1, 1]$로 rescale하고 $T = 80, \epsilon = 0.002$로 설정한다.

Diffusion model은 샘플링 속도가 느리다. 분명히 샘플링에 ODE solver를 사용하려면 score model $s_\phi (x, t)$의 반복 평가가 필요하며 이는 계산 비용이 많이 든다. 빠른 샘플링을 위한 기존 방법에는 더 빠른 numerical ODE solver와 distillation 기술이 포함된다. 그러나 ODE solver가 경쟁력 있는 샘플을 생성하려면 여전히 10개 이상의 평가 step이 필요하다. 대부분의 distillation 방법은 distillation 전에 diffusion model에서 대량의 샘플 데이터셋을 수집하는 데 의존하며, 그 자체로 계산 비용이 많이 든다. 이러한 단점을 겪지 않는 유일한 distillation 방식은 Progressive Distillation (PD)이다.

Consistency Models

본 논문은 디자인의 핵심에서 단일 step 생성을 지원하는 새로운 유형의 모델인 consistency model을 제안하는 동시에 샘플 품질과 계산 간의 절충을 위한 반복 생성과 zero-shot 데이터 편집을 허용한다. Consistency model은 distillation 모드 또는 isolation 모드에서 학습될 수 있다. 전자의 경우 consistency model은 사전 학습된 diffusion model의 지식을 단일 step 샘플러로 증류하여 샘플 품질에서 다른 distillation 접근법을 크게 개선하는 동시에 zero-shot 이미지 편집을 가능하게 한다. 후자의 경우 consistency model은 사전 학습된 diffusion model에 의존하지 않고 격리되어 학습되며, 이는 생성 모델의 독립적인 새로운 클래스로 만든다.

Definition

PF ODE의 솔루션 궤적 \(\{x_t\}_{t \in [\epsilon, T]}\)가 주어지면 consistency function을 $f : (x_t, t) \mapsto x_\epsilon$으로 정의한다. Consistency function은 다음과 같은 self-consistency 속성을 가지고 있다.

출력은 동일한 PF ODE 궤적에 속하는 $(x_t, t)$의 임의 쌍에 대해 일관된다.
즉, 모든 $t, t’ \in [\epsilon, T]$에 대해 $f (x_t, t) = f (x_{t’}, t’)$이다.

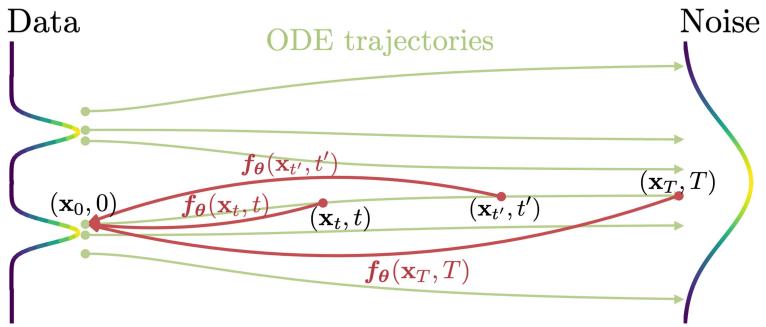
위 그림에서 볼 수 있듯이 consistency model $f_\theta$의 목표는 self-consistency 속성을 적용하는 방법을 학습하여 데이터에서 이 consistency function $f$를 추정하는 것이다. Neural ODE의 맥락에서 neural flow에 유사한 정의가 사용된다. 그러나 neural flow와 비교하여 consistency model은 가역적으로 강제되지 않는다.

Parameterization

모든 consistency function $f$에 대해 $f(x_\epsilon, \epsilon) = x_\epsilon$, 즉 $f(\cdot, \epsilon)$는 항등 함수이다. 이 제약 조건을 경계 조건이라고 한다. 이 경계 조건은 consistency model의 성공적인 학습에 중요한 역할을 하기 때문에 모든 consistency model은 이 경계 조건을 충족해야 한다. 이 경계 조건은 또한 consistency model에 대한 가장 제한적인 아키텍처 제약 조건이다. 신경망을 기반으로 하는 consistency model의 경우 이 경계 조건을 거의 무료로 구현하는 두 가지 방법이 있다. 출력이 $x$와 동일한 차원을 갖는 자유 형식 신경망 $F_\theta (x, t)$가 있다고 가정하자. 첫 번째 방법은 consistency model을 다음과 같이 간단히 parameterize하는 것이다.

\[\begin{equation} f_\theta (x, t) = \begin{cases} x & \quad t = \epsilon \\ F_\theta (x, t) & \quad t \in (\epsilon, T] \end{cases} \end{equation}\]

두 번째 방법은 다음과 같이 skip connection을 사용하여 consistency model을 parameterize하는 것이다.

\[\begin{equation} f_\theta (x, t) = c_\textrm{skip} (t) x + c_\textrm{out} (t) F_\theta (x, t) \end{equation}\]

여기서 $c_\textrm{skip} (t)$와 $c_\textrm{out} (t)$는 $c_\textrm{skip} (\epsilon) = 1$이고 $c_\textrm{out} (\epsilon) = 0$인 미분 가능한 함수이다.

이러한 방식으로 $F_\theta (x, t)$, $c_\textrm{skip} (t)$, $c_\textrm{out} (t)$가 모두 미분 가능하면 consistency model은 $t = \epsilon$에서 미분 가능하며, 이는 연속 시간 consistency model을 학습하는 데 중요하다. 두 번째 방법의 parameterization은 많은 성공적인 diffusion model과 매우 유사하므로 consistency model을 구성하기 위해 강력한 diffusion model 아키텍처를 쉽게 빌릴 수 있다. 따라서 모든 실험에서 두 번째 parameterization을 따른다.

Sampling

잘 학습된 consistency model $f_\theta$를 사용하여 초기 분포 \(\hat{x}_T = \mathcal{N} (0, T^2 I)\)에서 샘플링한 다음 \(\hat{x}_\epsilon = f_\theta (\hat{x}_T, T)\)에 대한 consistency model을 평가하여 샘플을 생성할 수 있다. 여기에는 consistency model을 통한 단 하나의 정방향 통과가 포함되므로 단일 step에서 샘플을 생성한다. 중요한 것은 샘플 품질 향상을 위해 denoising과 noise 주입 단계를 번갈아 가며 consistency model을 여러 번 평가할 수도 있다는 것이다.

Algorithm 1에 요약된 이 다단계 샘플링 절차는 컴퓨팅을 샘플 품질과 교환할 수 있는 유연성을 제공한다. 또한 zero-shot 데이터 편집에 중요하다. 실제로 Algorithm 1에서 시간 포인트 \(\{\tau_1, \cdots, \tau_{N-1}\}\)를 그리디 알고리즘으로 찾는다. 여기서 시간 포인트는 Algorithm 1에서 얻은 샘플의 FID를 최적화하기 위해 삼분 탐색 (ternary search)을 사용하여 한 번에 하나씩 정확히 지정된다. 이것은 주어진 이전 시점에서 FID가 다음 시점의 단봉 함수라고 가정한다.

Zero-Shot Data Editing

Diffusion model과 마찬가지로 consistency model은 zero-shot에서 다양한 데이터 편집 및 조작을 가능하게 한다. 이러한 작업을 수행하기 위해 명시적인 학습이 필요하지 않다. 예를 들어 consistency model은 가우시안 noise 벡터에서 데이터 샘플로의 일대일 매핑을 정의한다. GAN, VAE, normalizing flow와 같은 latent 변수 모델과 마찬가지로 consistency model은 latent space를 통과하여 샘플 간에 쉽게 보간할 수 있다. Consistency model은 $t \in [\epsilon, T]$인 모든 noisy한 입력 $x_t$에서 $x_\epsilon$를 복구하도록 학습되므로 다양한 noise 레벨에 대해 denoising을 수행할 수 있다. 또한 Algorithm 1의 다단계 생성 절차는 diffusion model과 유사한 반복 절차를 사용하여 zero-shot의 특정 inverse problem을 해결하는 데 유용하다. 이를 통해 SDEdit에서와 같이 인페인팅, colorization, super-resolution, stroke-guided 이미지 편집을 포함하여 이미지 편집 맥락에서 많은 애플리케이션을 사용할 수 있다.

Training Consistency Models via Distillation

사전 학습된 score model $s_\phi (x, t)$를 증류하여 consistency model을 학습하는 첫 번째 방법을 제시한다. 논의는 score model $s_\phi (x, t)$를 PF ODE에 연결하여 얻은 경험적 PF ODE를 중심으로 진행된다. 시간 지평 $[\epsilon, T]$를 경계 $t_1 = \epsilon < t_2 < \cdots < t_N = T$를 사용하여 $N - 1$개의 하위 간격으로 discretize하는 것을 고려하자. 저자들은 EDM을 따라

\[\begin{equation} t_i = (\epsilon^{1/\rho} + \frac{i-1}{N-1} (T^{1/\rho} - \epsilon^{1/\rho}))^\rho, \quad \rho = 7 \end{equation}\]

로 경계들을 결정하였다. $N$이 충분히 크면 numerical ODE solver의 discretization step을 한 번 실행하여 $x_{t_{n+1}}$에서 $x_{t_{n}}$의 정확한 추정치를 얻을 수 있다. 이 추정치 \(\hat{x}_{t_n}^\phi\)는 다음과 같이 정의된다.

\[\begin{equation} \hat{x}_{t_n}^\phi := x_{t_{n+1}} + (t_n - t_{n+1}) \Phi (x_{t_{n+1}}, t_{n+1}; \phi) \end{equation}\]

여기서 $\Phi$는 경험적 PF ODE에 적용된 one-step ODE solver의 업데이트 함수이다. 예를 들어 Euler solver를 사용할 때 다음 업데이트 규칙에 해당하는 $\Phi (x, t; \phi) = - t s_\phi (x, t)$가 있다.

\[\begin{equation} \hat{x}_{t_n}^\phi = x_{t_{n+1}} - (t_n - t_{n+1}) t_{n+1} s_\phi (x_{t_{n+1}}, t_{n+1}) \end{equation}\]

단순화를 위해 본 논문에서는 one-step ODE solver만 고려한다.

PF ODE와 SDE 간의 연결로 인해 먼저 $x \sim p_\textrm{data}$를 샘플링한 다음 $x$에 Gaussian noise를 추가하여 ODE 궤적 분포를 따라 샘플링할 수 있다. 구체적으로, 데이터 포인트 $x$가 주어지면, 데이터셋에서 $x$를 샘플링하여 효율적으로 PF ODE 궤적에서 한 쌍의 인접한 데이터 포인트 \((\hat{x}_{t_n}^\phi, x_{t_{n+1}})\)를 생성할 수 있다. SDE의 transition 밀도 $\mathcal{N} (x, t_{n+1}^2 I)$에서 $x_{t_{n+1}}$을 샘플링한 다음 numerical ODE solver의 하나의 discretization step을 사용하여 \(\hat{x}_{t_n}^\phi\)을 계산한다. 그런 다음 \((\hat{x}_{t_n}^\phi, x_{t_{n+1}})\)에 대한 출력 차이를 최소화하여 consistency model을 학습시킨다. 이는 consistency model 학습을 위해 다음과 같은 consistency distillation (CD) loss을 사용하도록 동기를 부여하였다.

\[\begin{equation} \mathcal{L}_\textrm{CD}^N (\theta, \theta^{-}; \phi) := \mathbb{E} [\lambda (t_n) d (f_\theta (x_{t_{n+1}}, t_{n+1}), f_{\theta^{-}} (\hat{x}_{t_n}^\phi, t_n))] \\ \textrm{where} \quad x \sim p_\textrm{data}, \quad n \sim \mathcal{U} [1, N-1], \quad x_{t_{n+1}} \sim \mathcal{N} (x; t_{n+1}^2 I) \end{equation}\]

여기서 $\lambda (\cdot) \in \mathbb{R}^{+}$는 양의 가중 함수이고, $\theta^{-}$는 최적화 과정에서 $\theta$의 과거 값의 running average이다. $d (\cdot, \cdot)$은 모든 $x$와 $y$에 대하여 $d(x, y) \ge 0$이고 $x = y$인 경우에만 $d(x, y) = 0$인 metric function이다.

본 논문의 실험에서는 제곱 $\ell_2$ 거리 $d(x, y) = | x - y |_2^2$, $\ell_1$ 거리 $d(x, y) = | x - y |_1$, LPIPS를 고려하였다. 저자들은 $\lambda (t_n) = 1$이 모든 task와 데이터셋에서 잘 수행됨을 발견했다. 실제로 exponential moving average (EMA)로 $\theta^{-}$를 업데이트하는 동안 모델 파라미터 $\theta$에 대한 SGD로 목적 함수를 최소화한다. 즉, 감쇠율 $0 \le \mu < 1$이 주어지면 각 최적화 step 후에 다음 업데이트를 수행한다.

\[\begin{equation} \theta^{-} \leftarrow \textrm{stopgrad} (\mu \theta^{-} + (1 - \mu) \theta) \end{equation}\]

전체 학습 절차는 Algorithm 2에 요약되어 있다. 강화 학습과 모멘텀 기반 contrastive learning의 관례에 따라 $f_{\theta^{-}}$를 “타겟 네트워크”로, $f_\theta$를 “온라인 네트워크”라고 한다. 단순히 $\theta^{-} = \theta$를 설정하는 것과 비교하여 EMA 업데이트와 “stopgrad” 연산자가 학습 프로세스를 크게 안정화하고 consistency model의 최종 성능을 향상시킬 수 있다.

$\theta^{-}$는 $\theta$의 과거에 대한 running average이므로 Algorithm 2의 최적화가 수렴할 때 $\theta^{-} = \theta$가 된다. 즉, 타겟 및 온라인 consistency model은 결국 서로 일치한다. 추가로 CD loss가 0이 되면 일부 규칙성 조건에서 ODE solver의 step 크기가 충분히 작은 한 임의로 정확해질 수 있다. 중요한 것은 경계 조건 $f_\theta (x, \epsilon) = x$는 consistency model 학습에서 발생하는 자명한 해 $f_\theta (x, t) = 0$을 배제한다는 것이다.

CD loss \(\mathcal{L}_\textrm{CD}^N (\theta, \theta^{-}; \phi)\)는 $\theta^{-} = \theta$ 또는 $\theta^{-} = \textrm{stopgrad} (\theta)$인 경우 무한히 많은 timestep ($N \rightarrow \infty$) 동안 유지되도록 확장될 수 있다. 연속 시간 loss function은 $N$ 또는 timestep \(\{t_1, \cdots, t_N\}\)를 지정할 필요가 없다. 그럼에도 불구하고 그들은 Jacobian-vector product를 포함하고 효율적인 구현을 위해 순방향 자동 미분을 요구하는데, 이는 일부 딥러닝 프레임워크에서 잘 지원되지 않을 수 있다.

Training Consistency Models in Isolation

사전 학습된 diffusion model에 의존하지 않고 consistency model을 학습할 수 있다. 이는 기존의 diffusion distillation 기술과 다르며 consistency model을 새롭고 독립적인 생성 모델로 만든다.

CD에서는 사전 학습된 score model $s_\phi (x, t)$를 사용하여 ground-truth score function $\nabla \log p_t (x)$를 근사화한다. 다음과 같은 편향되지 않은 estimator를 활용하여 이 사전 학습된 score model의 사용을 모두 피할 수 있다.

\[\begin{equation} \nabla \log p_t (x_t) = - \mathbb{E} \bigg[ \frac{x_t - x}{t^2} \bigg\vert x_t \bigg] \\ \textrm{where} \quad x \sim p_\textrm{data}, \quad x_t \sim \mathcal{N} (x; t^2 I) \end{equation}\]

즉, $x$와 $x_t$가 주어지면 $-(x_t - x)/t^2$으로 $\log \nabla p_t (x_t)$를 추정할 수 있다. 이 편향되지 않은 추정은 $N \rightarrow \infty$에서 Euler solver를 사용할 때 CD에서 사전 학습된 diffusion model을 대체하기에 충분하다.

Consistency training (CT) loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{CT}^N (\theta, \theta^{-}) := \mathbb{E} [\lambda (t_n) d(f_\theta (x + t_{n+1} z, t_{n+1}), f_{\theta^{-}} (x + t_n z, t_n))] \\ \textrm{where} \quad z \sim \mathcal{N} (0,I), \quad x \sim p_\textrm{data}, \quad x_{t_{n+1}} \sim \mathcal{N} (x; t_{n+1}^2 I) \end{equation}\]

저자들은 실제 성능 향상을 위해 schedule function $N (\cdot)$에 따라 학습 중에 $N$을 점진적으로 증가시킬 것을 제안한다. $N$이 작을 때 (즉, $\Delta t$가 클 때) 기본 CD loss와 관련하여 CT loss가 “분산”이 적지만 “편향”이 더 커서 학습 시작 시 더 빠른 수렴을 용이하게 한다는 것이 직관적이다. 반대로, $N$이 크면 (즉, $\Delta t$가 작으면) “분산”은 더 많지만 “편향”은 적다. 이는 학습의 끝에 가까워질수록 바람직하다. 최상의 성능을 위해 schedule function $\mu (\cdot)$에 따라 $\mu$가 $N$과 함께 변경되어야 한다. CT의 전체 알고리즘은 Algorithm 3에서 제공된다.

CD와 유사하게 CT loss \(\mathcal{L}_\textrm{CT}^N (\theta, \theta^{-})\)는 $\theta^{-} = \textrm{stopgrad} (\theta)$인 경우 연속 시간 (즉, $N \rightarrow \infty$)에서 유지되도록 확장될 수 있다. 이 연속 시간 loss function은 $N$ 또는 $\mu$에 대한 schedule function이 필요하지만 효율적인 구현을 위해 순방향 자동 미분을 필요로 한다. 이산 시간 CT loss와 달리 Algorithm 2에서 $\Delta t \rightarrow 0$을 효과적으로 취하기 때문에 연속 시간 목적 함수와 관련된 바람직하지 않은 “편향”은 없다.

Experiments

1. Training Consistency Models

다음은 CIFAR-10에서 CD와 CT에 영향을 미치는 다양한 요인들에 대한 그래프이다.

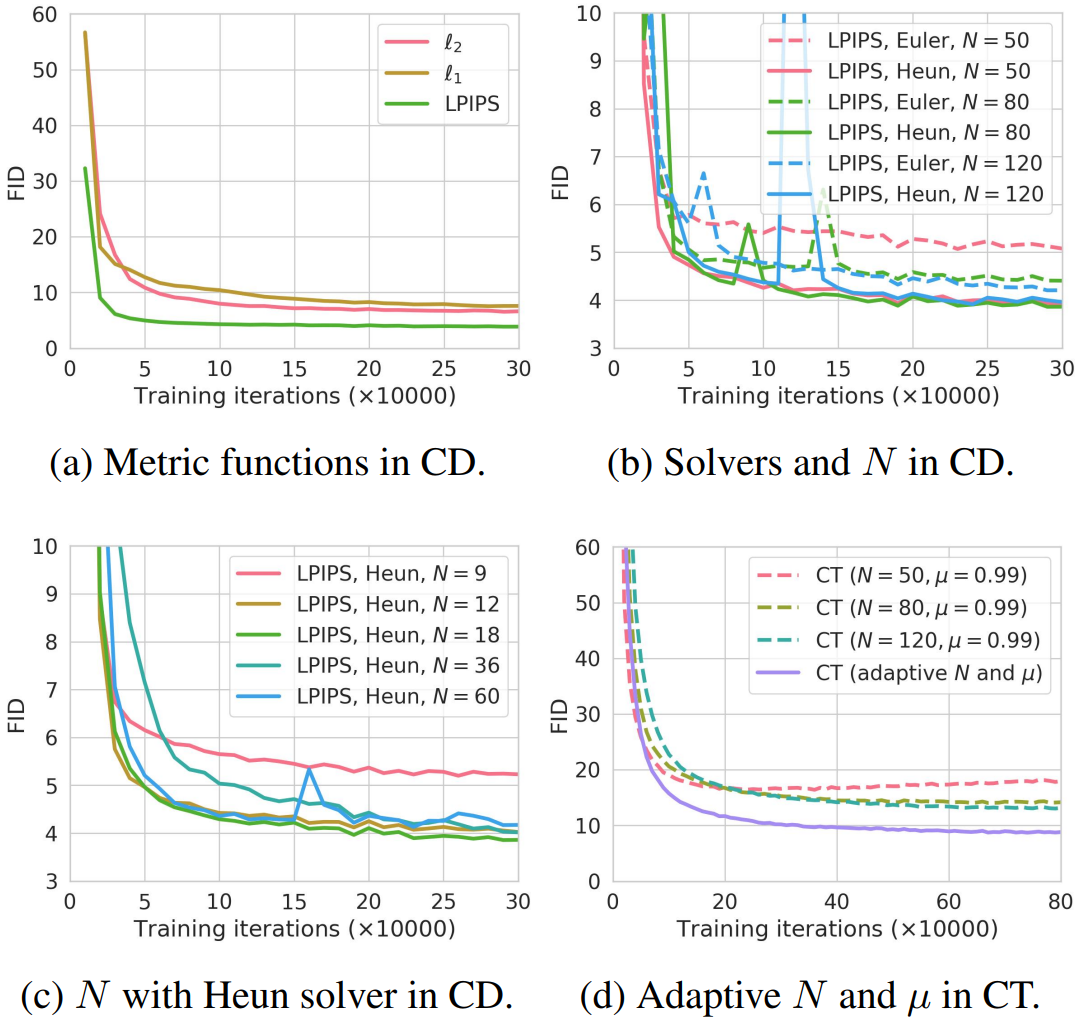
CD를 위한 최적의 metric은 LPIPS이며, Heun ODE solver와 $N = 18$가 최적의 선택이다. 또한 $N$과 $\mu$의 적응형 schedule은 CT의 수렴 속도와 샘플 품질을 크게 향상시킨다.

2. Few-Step Image Generation

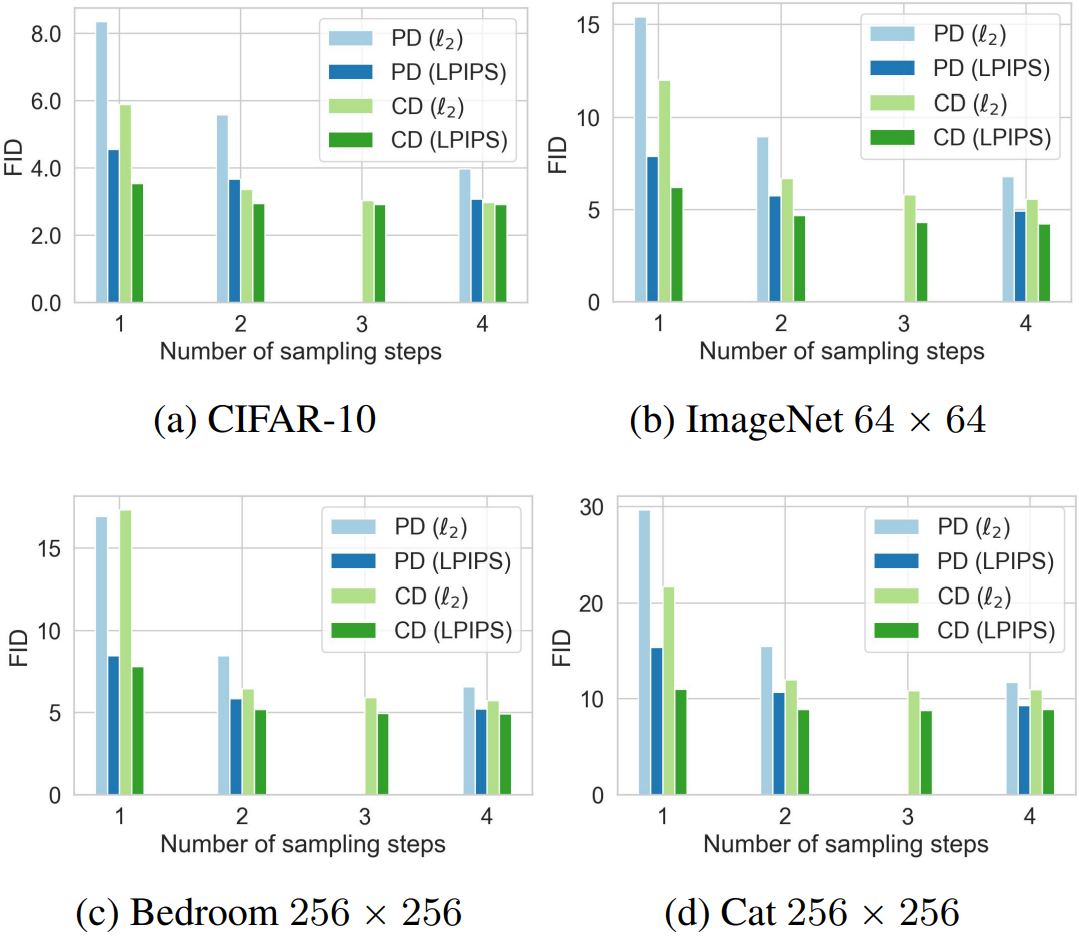
다음은 consistency distillation (CD)를 사용한 다단계 이미지 생성 성능을 progressive distillation (PD)와 비교한 그래프이다.

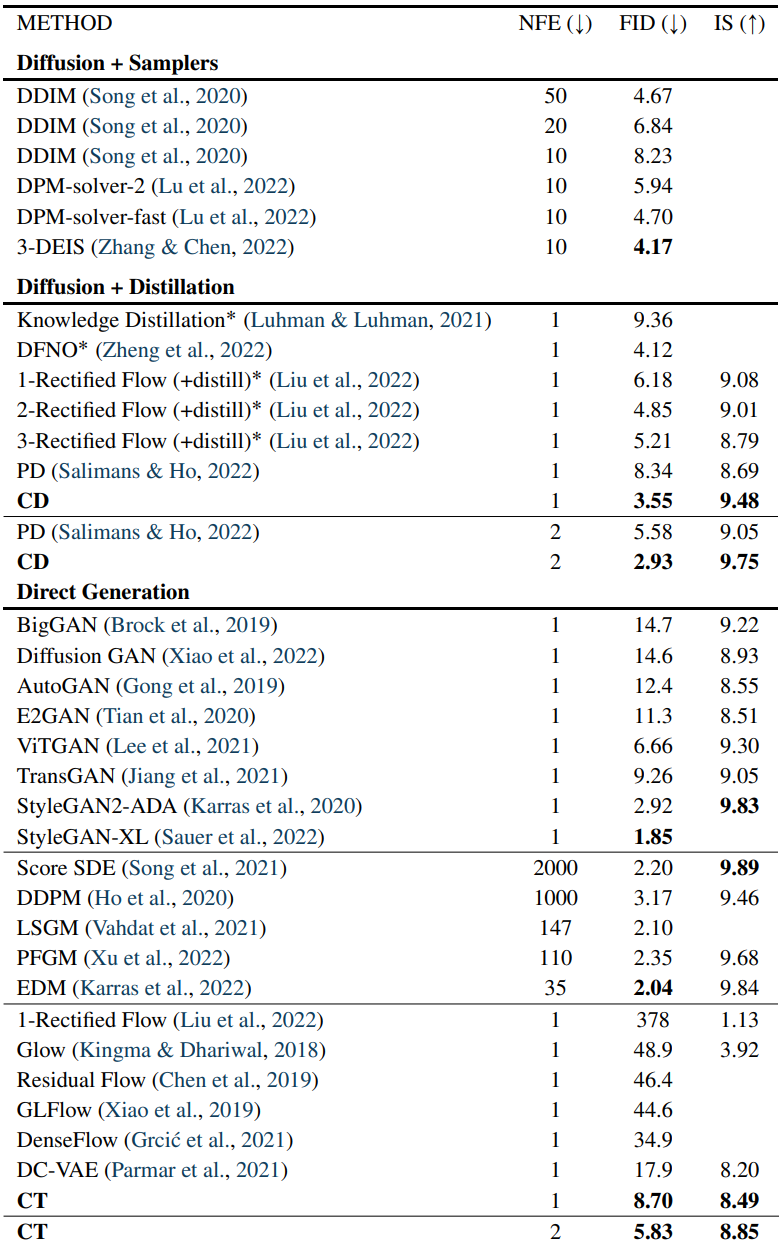
다음은 CIFAR-10에서의 샘플 품질을 비교한 표이다.

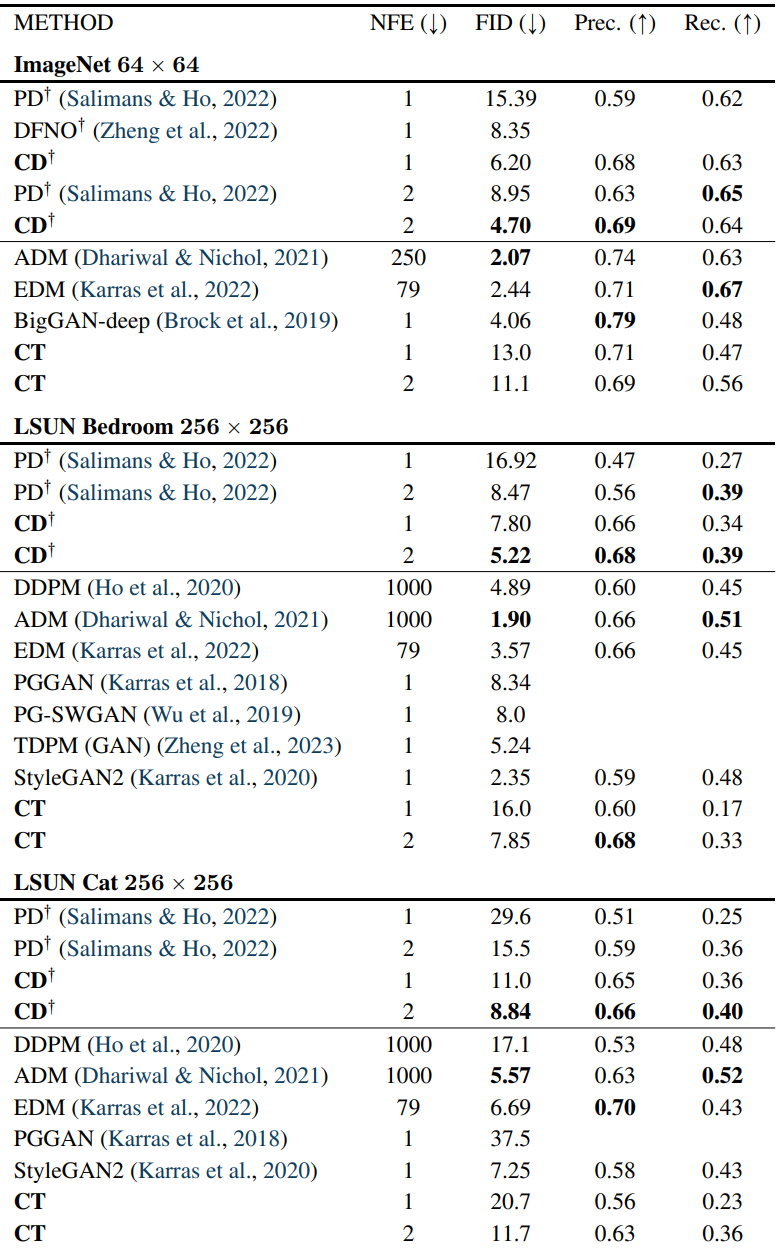
다음은 ImageNet 64$\times$64와 LSUN Bedroom & Cat 256$\times$256에서의 샘플 품질을 비교한 표이다.

다음은 EDM (상단), CT + single-step 생성 (중단), CT + 2-step 생성 (하단) 결과를 비교한 것이다.

3. Zero-Shot Image Editing

LSUN Bedroom 256$\times$256에서 CD로 학습된 consistency model을 사용한 zero-shot 이미지 편집 결과이다.