[논문리뷰] Scalable High-Resolution Pixel-Space Image Synthesis with Hourglass Diffusion Transformers
ICML 2024. [Paper] [Page] [Github]
Katherine Crowson, Stefan Andreas Baumann, Alex Birch, Tanishq Mathew Abraham, Daniel Z. Kaplan, Enrico Shippole
Stability AI | LMU Munich | Birchlabs
21 Jan 2024

Introduction
Diffusion model은 CNN, Transformer, CNN-transformer-hybrid, state-space model에 이르기까지 사용되는 backbone 아키텍처가 다양하다. 고해상도 이미지 합성을 위해 이러한 모델들을 확장하는 데 사용되는 접근 방식에도 여러 가지가 있다. 현재 접근 방식은 학습에 복잡성을 더하고, 추가 모델을 필요로 하거나 품질을 희생한다.
Latent diffusion model은 고해상도 이미지 합성을 위한 주요 방법이지만, 미세한 디테일을 표현하지 못하여 샘플 품질에 영향을 미치고 이미지 편집과 같은 응용에서의 유용성을 제한한다.
본 논문은 backbone 개선을 통한 고해상도 합성을 다루며, Hourglass Transformer에서 소개된 계층적 구조에서 영감을 받은 순수 Transformer 아키텍처를 소개한다. 이를 Hourglass Diffusion Transformer (HDiT)라고 한다.
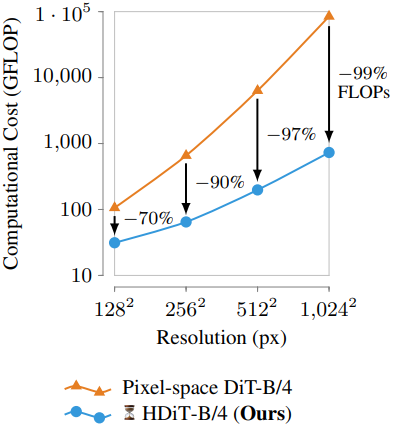
다양한 아키텍처 개선 사항을 도입하여 표준 diffusion 설정에서 메가픽셀 규모로 고품질 이미지를 생성할 수 있는 backbone을 얻는다. 이 아키텍처는 128$\times$128과 같은 낮은 공간 해상도에서도 DiT보다 훨씬 더 효율적이며, 생성 품질 면에서 경쟁력이 있다. 모델 아키텍처를 다른 대상 해상도에 맞게 조정하는 본 논문의 방법을 사용하여 DiT 아키텍처의 $O(n^2)$ 스케일링 대신 $O(n)$ 스케일링을 얻는다. 이를 통해 convolutional U-Net과 계산 복잡도 면에서 경쟁력이 있는 최초의 Transformer 기반 diffusion backbone 아키텍처가 되었다.
Method
DiT는 latent diffusion 설정에서 인상적인 성능을 보여주었으며, 생성 품질 측면에서 이전 방법들을 능가했다. 그러나 고해상도에 대한 확장성은 계산 복잡도가 이차적으로 증가한다는 사실에 의해 제한된다. 이는 고해상도 입력을 학습하고 실행하는 데 과도한 비용을 초래하며, 실질적으로 Transformer를 충분히 작은 차원의 공간으로 압축된 latent들로 제한시킨다. 대규모 패치 크기를 사용하는 경우를 제외하면 이는 생성된 샘플의 품질에 부정적인 영향을 미치는 것으로 밝혀졌다.
본 논문은 DiT와 Hourglass Transformer를 기반으로 하는 계층적 아키텍처인 Hourglass Diffusion Transformer (HDiT)를 제안하였다. HDiT는 고품질 픽셀 공간 이미지 생성을 가능하게 하고 $O(n^2)$ 대신 $O(n)$의 계산 복잡도 스케일링으로 더 높은 해상도에 효율적으로 적응할 수 있다. 즉, 메가픽셀 해상도에서 직접 픽셀 공간 생성으로 확장하는 것도 실행 가능해진다.
1. Leveraging the Hierarchical Nature of Image
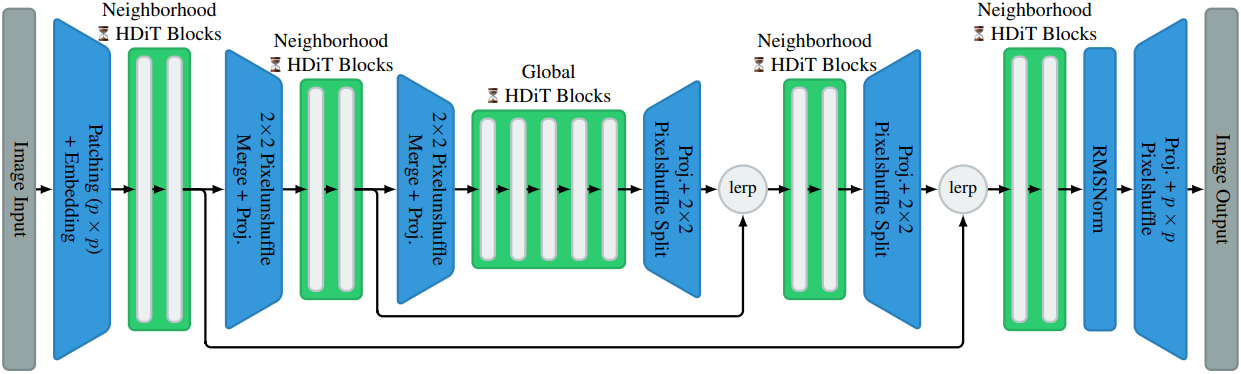
이미지는 계층적 구조를 보인다. 이는 diffusion model에서 일반적으로 사용되는 U-Net 아키텍처에 성공적으로 적용되었지만 diffusion transformer에서는 일반적으로 사용되지 않는다. Transformer backbone에 이미지의 이러한 계층적 특성을 활용하기 위해, 이미지를 포함한 다양한 모달리티에 효과적인 것으로 입증된 모래시계 구조를 적용한다. 모델의 기본 해상도에 따라 계층 구조의 레벨 수를 선택하여 가장 안쪽 레벨에 16$\times$16 토큰이 있도록 한다. 낮은 해상도 레벨은 낮은 해상도 정보와 높은 해상도 레벨을 따르는 데 관련된 정보를 모두 처리해야 하므로 더 큰 hidden dimension을 선택한다. 인코더 측의 모든 레벨에 대해 PixelUnShuffle을 사용하여 2$\times$2 토큰을 공간적으로 하나로 병합하고 디코더 측에서 그 반대를 수행한다.
Skip Merging Mechanism
이러한 아키텍처에서 중요한 고려 사항 중 하나는 skip connection의 병합 메커니즘으로, 최종 성능에 상당한 영향을 미칠 수 있다. 저자들은 U-Net과 유사한 concat 기반의 구현보다 가산적 skip connection이 더 나은 성능을 보인다는 것을 발견했다. Skip이 제공하는 정보의 유용성은 특히 매우 깊은 레이어에서 상당히 다를 수 있으므로, 모델이 skip된 branch와 업샘플링된 branch의 상대적 중요성을 학습할 수 있도록 둘 사이의 linear interpolation (lerp) 계수 $f$를 학습시키고 이를 다음과 같이 구현한다.
\[\begin{equation} \textbf{x}_\textrm{merged}^{(l, \textrm{lerp})} = f \cdot \textbf{x}_\textrm{skip} + (1 - f) \cdot \textbf{x}_\textrm{upsampled} \end{equation}\]2. Hourglass Diffusion Transformer Block Design
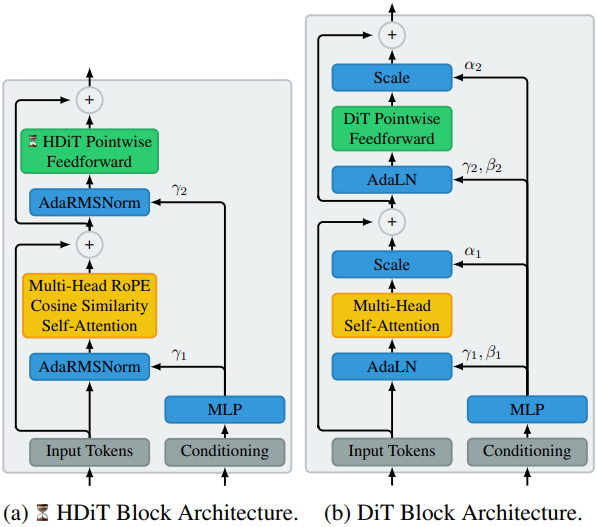
기본 Transformer block 설계는 LLaMA의 block에서 영감을 받았다. 조건부 처리를 가능하게 하기 위해 RMSNorm 연산에서 사용하는 출력 스케일을 적응형으로 설정하고, 클래스와 diffusion timestep에 조건부로 동작하는 매핑 네트워크가 이를 예측하도록 구성했다. DiT와는 달리, 적응형 출력 게이트를 사용하지 않으며, 대신 self-attention과 FFN block의 출력 projection을 0으로 초기화한다.
Transformer 모델이 위치 정보를 활용할 수 있도록 하기 위해, 일반적인 diffusion transformer 아키텍처에서는 학습 가능한 가산적 위치 인코딩을 사용하였다. 그러나 저자들은 모델의 일반화 성능과 새로운 시퀀스 길이에 대한 외삽 능력을 향상시키는 것으로 알려진 RoPE (Rotary Positional Embedding)를 2D 이미지 데이터에 적응시켜 사용했다. 이를 위해 Axial Transformer를 따라 축별로 인코딩을 나누고, 각각의 공간 축에 대해 query와 key의 서로 다른 부분에 RoPE를 적용하였다. 또한, 저자들은 query와 key 벡터의 절반에만 이 인코딩 방식을 적용하고 나머지는 수정하지 않는 것이 성능에 유리하다는 것을 발견했다.
결과적으로, 저자들은 가산적 위치 인코딩을 적응형 RoPE로 대체하면 수렴 속도가 개선되고 패치 아티팩트를 줄이는 데 도움이 된다는 것을 실험적으로 확인했다. RoPE를 적용하는 것 외에도, Swin Transformer V2에 사용된 코사인 유사도 기반 attention 메커니즘을 채택했다.
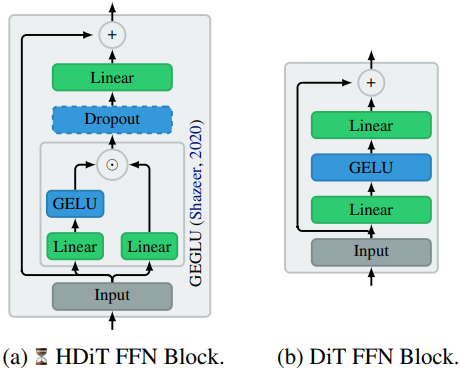
Feedforward block의 경우 DiT와 같은 출력 게이트 대신 GEGLU를 사용한다. 여기서 변조 신호는 컨디셔닝 대신 데이터 자체에서 나오고 FFN의 두 번째 레이어 대신 첫 번째 레이어에 적용된다.
3. Efficient Scaling to High Resolutions
모래시계 구조는 다양한 해상도에서 이미지를 처리할 수 있게 해준다. 낮은 해상도에서 global self-attention을 사용하여 일관성을 얻고, 모든 높은 해상도에서 local self-attention을 사용하여 디테일을 향상시킨다. 이는 계산 복잡도가 제곱에 비례하는 global attention의 필요성을 관리 가능한 양으로 제한하고, 선형적인 복잡도로 해상도를 더 증가시킨다. 점근적으로 복잡도는 픽셀 수 $n$에 대해 $O(n)$이다.
Local self-attention에 대한 일반적인 선택은 Shifted Window attention이다. 그러나 저자들은 Neighborhood attention가 실제로 상당히 더 나은 성능을 보인다는 것을 발견했다.
Global self-attention을 적용할 최대 해상도는 데이터셋과 task에 의해 결정되는 선택이다. 특히 낮은 해상도(ex. 256$\times$256)에서 일부 데이터셋은 더 적은 레벨들의 global attention으로 일관된 생성을 허용한다.
Experiments
- 학습 디테일
- optimizer: AdamW
- learning rate: $5 \times 10^{-4}$
- weight decay: 0.01
- batch size: 256
- step: 40만
- EMA decay: 0.9999
- 샘플링: DPM++ (50 step)
저자들은 낮은 noise level에서 SNR weighting에 비해 loss 가중치를 줄이는, soft-min-snr이라고 불리는 적응형 min-snr loss weighting 방법에 대해서도 논의하였다. SNR weighting, Min-SNR weighting, soft-min-snr weighting은 각각 다음과 같다.
\[\begin{equation} w_\textrm{SNR} (\sigma) = \frac{1}{\sigma^2}, \quad w_\textrm{Min-SNR} (\sigma) = \min \bigg\{ \frac{1}{\sigma^2}, \gamma \bigg\} \\ w_\textrm{Soft-Min-SNR} (\sigma) = \frac{1}{\sigma^2 + \gamma^{-1}} \end{equation}\]1. Effect of the Architecture
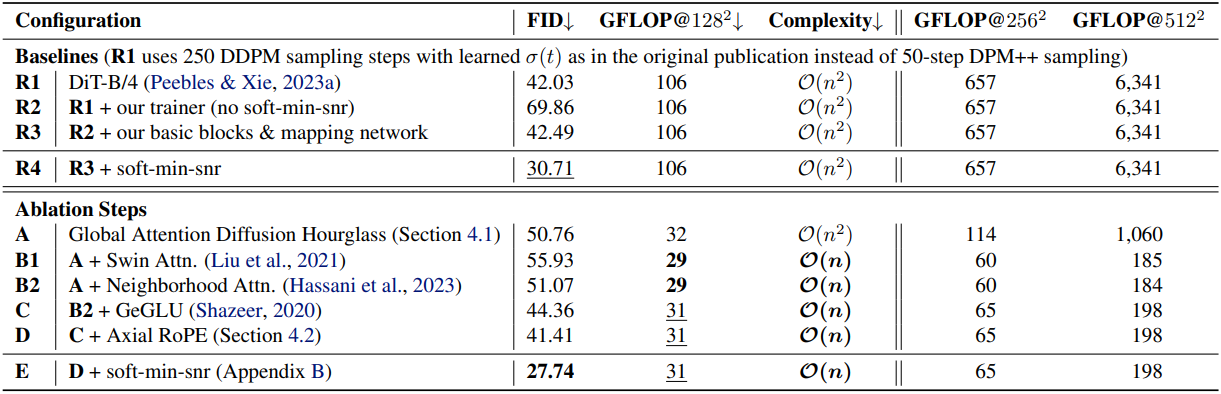
다음은 아키텍처에 대한 ablation 결과이다.
다음은 skip 정보 융합 메커니즘에 대한 ablation 결과이다.

2. High-Resolution Pixel-Space Image Synthesis
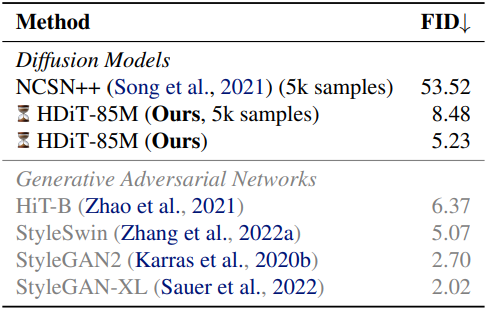
다음은 FFHQ 1024$\times$1024에서의 비교 결과이다.

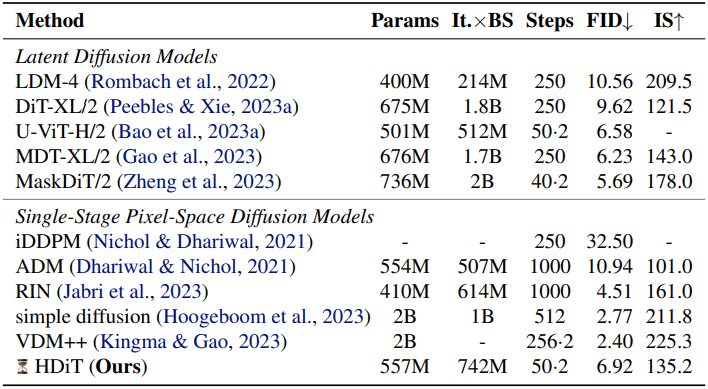
3. Large-Scale ImageNet Image Synthesis
다음은 ImageNet 256$\times$256에서의 비교 결과이다.