[논문리뷰] Structured Denoising Diffusion Models in Discrete State-Spaces (D3PM)
NeurIPS 2021. [Paper] [Github]
Jacob Austin, Daniel D. Johnson, Jonathan Ho, Daniel Tarlow, Rianne van den Berg
Google Research, Brain Team
7 Jul 2021
Introduction
최근 diffusion model은 이미지 및 오디오 생성을 위한 매력적인 대안으로 등장하여 GAN에 필적하는 샘플 품질과 더 적은 inference step으로 autoregressive model에 필적하는 log-likelihood를 달성한다. Diffusion model은 학습 데이터를 순수한 noise로 점진적으로 손상시키도록 구성된 미리 정의된 forward process를 reverse시키도록 학습된 parameterize된 Markov chian이다. Diffusion model은 최대 likelihood와 score matching과 밀접하게 관련된 안정적인 목적 함수를 사용하여 학습되며 병렬 반복 정제를 사용하여 autoregressive model보다 더 빠른 샘플링이 가능하다.
Diffusion model이 discrete state space와 continuous state space 모두에서 제안되었지만 최근 연구는 continuous state space에서 작동하는 Gaussian diffusion process에 중점을 두었다. Discrete state space가 있는 diffusion model은 텍스트 및 이미지 segmentation 도메인에 대해 탐색되었지만 대규모 텍스트 또는 이미지 생성을 위한 모델 클래스로 아직 입증되지 않았다.
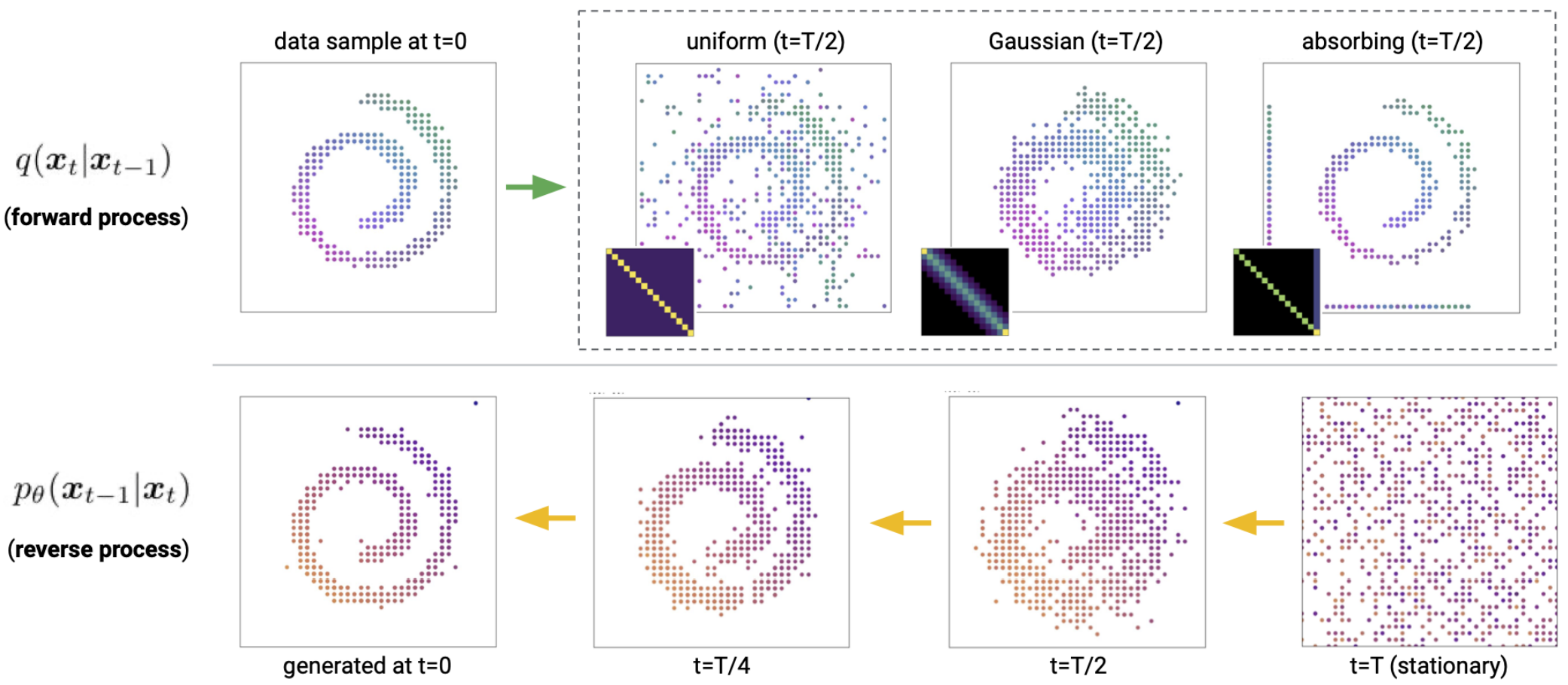
본 논문의 목표는 위 그림과 같이 데이터 생성을 형성하기 위해 보다 구조화된 카테고리형 손상 프로세스를 사용하여 discrete diffusion model을 개선하고 확장하는 것이다. 본 논문의 모델은 이산 데이터(이미지 포함)를 완화하거나 continuous space에 포함할 필요가 없다. Forward process에서 사용되는 transition 행렬에 구조 또는 도메인 지식을 내장할 수 있으며, 이러한 유연성을 활용하여 상당히 개선된 결과를 얻는다. 토큰 간의 유사성을 사용하여 점진적인 손상 및 denoising을 가능하게 하는 텍스트 데이터에 적합한 구조화된 손상 프로세스를 개발한다. 더 확장하여 토큰을 삽입하는 손상 프로세스도 탐색하여 autoregressive 및 마스크 기반 생성 모델과 유사점이 있다. Continuous diffusion model이 활용하는 locality에서 영감을 얻어 양자화된 이미지에 대한 discrete diffusion model을 연구한다. 이는 더 유사한 state로 우선적으로 diffuse되고 이미지 도메인에서 훨씬 더 나은 결과를 가져오는 discrete 손상 프로세스의 특정 선택으로 이어진다.
Diffusion models for discrete state space
$K$개의 카테고리 $x_t, x_{t−1} \in 1, \cdots, K$가 있는 스칼라 이산 확률 변수의 경우 forward transition 확률은 행렬로 나타낼 수 있다.
\[\begin{equation} [Q_t]_{ij} = q(x_t = j \vert x_{t-1} = i) \end{equation}\]행 벡터 $x$로 $x$의 one-hot 버전을 나타내면 다음과 같이 쓸 수 있다.
\[\begin{equation} q(x_t \vert x_{t-1}) = \textrm{Cat} (x_t; p = x_{t-1} Q_t) \end{equation}\]여기서 $\textrm{Cat}(x;p)$는 행 벡터 $p$에 의해 주어진 확률을 갖는 one-hot 행 벡터 $x$에 대한 카테고리형 분포이고 $x_{t-1} Q_t$는 행 벡터-행렬 곱이다. 저자들은 $Q_t$가 이미지의 각 픽셀 또는 시퀀스의 각 토큰에 독립적으로 적용되고 $q$가 이러한 더 높은 차원에서도 분해된다고 가정한다. 따라서 $q(x_t \vert x_{t-1})$을 단일 요소로 쓴다. $x_0$부터 시작하여 시간 $t−1$에서 다음과 같은 $t$-step marginal과 posterior를 얻는다.
\[\begin{aligned} q(x_t \vert x_0) &= \textrm{Cat} (x_t; p=x_0 \bar{Q}_t), \quad \textrm{with } \bar{Q}_t = Q_1 Q_2 \cdots Q_t \\ q(x_{t-1} \vert x_t, x_0) &= \frac{q(x_t \vert x_{t-1}, x_0) q(x_{t-1} \vert x_0)}{q(x_t \vert x_0)} = \textrm{Cat} \bigg( x_{t-1}; p = \frac{x_t Q_t^\top \odot x_0 \bar{Q}_{t-1}}{x_0 \bar{Q}_t x_t^\top} \bigg) \end{aligned}\]Forward process의 Markov 속성으로 인해 $q(x_t \vert x_{t−1}, x_0) = q(x_t \vert x_{t−1})$이다. Reverse process $p_\theta (x_t \vert x_{t-1})$도 이미지 또는 시퀀스 요소에 대해 조건부 독립으로 분해된다고 가정하면, $q$와 $p_\theta$ 사이의 KL divergence는 각 확률 변수의 모든 가능한 값을 간단히 합산하여 계산할 수 있다. $Q_t$에 따라 누적 곱 $\bar{Q}_t$는 종종 closed form으로 계산되거나 단순히 모든 $t$에 대해 미리 계산될 수 있다.
여기서부터는 discrete state space를 갖는 diffusion model의 일반 클래스를 Discrete Denoising Diffusion Probabilistic Model (D3PM)이라고 한다.
1. Choice of Markov transition matrices for the forward process
위에서 설명한 D3PM 프레임워크의 장점은 $Q_t$를 선택하여 데이터 손상 및 denoising process를 제어할 수 있다는 점이다. 이는 부가적인 Gaussian noise만이 상당한 주목을 받은 continuous diffusion과는 대조적이다. $Q_t$의 행의 합이 1이 되어야 한다는 제약 외에 $Q_t$를 선택할 때 유일한 제약은 $t$가 커질 때 $\bar{Q}_t = Q_1 Q_2 \cdots Q_t$의 행이 알려진 stationary distribution로 수렴해야 한다는 것이다. 이는 $Q_t$에 최소한의 제한을 가하면서 보장할 수 있다.
저자들은 이미지와 텍스트를 포함한 대부분의 실제 이산 데이터에 대해 forward process와 학습 가능한 reverse process를 제어하는 방법으로 transition 행렬 $Q_t$에 도메인 종속 구조를 추가하는 것이 합리적이라고 주장한다. 이미지 및 텍스트 데이터셋 실험을 위해 탐색한 일련의 transition 행렬은 다음과 같다.
- Uniform: Deep unsupervised learning using nonequilibrium thermodynamics 논문은 이진 확률 변수에 대한 간단한 2$\times$2 transition 행렬을 고려했다. Argmax flows and multinomial diffusion 논문은 나중에 이것을 카테고리형 변수로 확장하여 transition 행렬 $Q_t = (1 − \beta_t)I + (\beta_t / K) 𝟙𝟙^\top \; (\beta_t \in [0, 1])$를 제안했다. 이 transition 행렬은 doubly stochastic matrix이므로 stationary distribution가 균일하다. 다른 state로의 transition 확률이 일정하기 때문에 본 논문에서는 이 discrete diffusion 인스턴스를 D3PM-uniform이라고 한다.
- Absorbing state: BERT의 성공과 텍스트의 Conditional Masked Language Models (CMLM)에 대한 최근 연구에 힘입어 absorbing state([MASK]라고 함)가 있는 transition 행렬을 고려하여 각 토큰이 동일하게 유지되거나 확률 $\beta_t$로 전환된다. 이는 uniform diffusion과 유사하게 카테고리 간에 특정 관계를 부과하지 않지만 여전히 손상된 토큰을 원래 토큰과 구별할 수 있다. 게다가, stationary distribution는 균일하지 않고 토큰에 모든 mass를 가지고 있다. 이미지의 경우 회색 픽셀을 absorbing 토큰으로 재사용한다.
- Discretized Gaussian: 다른 state로 균일하게 전환하는 대신 순서형 데이터의 경우 이산화되고 절단된 가우시안 분포를 사용하여 continuous space diffusion model을 모방할 것을 제안한다. Transition 행렬이 doubly stochastic matrix이므로 균일한 stationary distribution으로 이어지는 정규화를 선택한다. 이 transition 행렬은 더 높은 확률로 더 유사한 state 간에 전이하며 이미지와 같은 양자화된 순서형 데이터에 매우 적합하다.
- Token embedding distance: 텍스트 데이터에는 순서 구조가 없지만 여전히 흥미로운 semantic 관계가 있을 수 있다. 예를 들어 문자 수준에서 모음은 자음보다 서로 더 유사할 수 있다. D3PM 프레임워크의 일반성을 보여주기 위해 임베딩 space에서 유사성을 사용하여 forward process를 안내하고 균일한 stationary distribution을 유지하면서 유사한 임베딩을 가진 토큰 간에 더 자주 전환하는 doubly stochastic transition matrix를 구성한다.
Uniform diffusion과 absorbing state diffusion의 경우 누적 곱 $\bar{Q}_t$는 closed form으로 미리 계산할 수 있다.
2. Noise schedules
Forward process의 noise schedule에 대해 여러 가지 옵션을 고려한다. Discretized Gaussian diffusion의 경우 가우시안 분산을 discretize하기 전에 선형적으로 증가시키는 방법을 탐색한다. Uniform diffusion의 경우 코사인 함수로의 transition 누적 확률을 설정하는 cosine schedule을 사용한다. 일반적인 transition 행렬 $Q_t$의 집합의 경우 이전에 제안된 schedule을 직접 적용할 수 없다. $x_t$와 $x_0$ 사이의 mutual information을 0으로 선형 보간하는 것을 고려한다.
\[\begin{equation} I(x_t; x_0) \approx (1 − \frac{t}{T}) H (x_0) \end{equation}\]흥미롭게도, absorbing-state D3PM의 특정 경우에 대해 이 일정은 Bernoulli diffusion process를 위해 제안된 $(T-t+1)^{-1}$ schedule와 같다.
3. Parameterization of the reverse process
신경망 \(\textrm{nn}_\theta (x_t)\)를 사용하여 $p_\theta (x_{t-1} \vert x_t)$의 로짓을 직접 예측하는 것이 가능하지만 \(\tilde{p}_\theta (\tilde{x}_0 \vert x_t)\)의 로짓을 예측하기 위해 신경망 \(\textrm{nn}_\theta (x_t)\)을 사용하는 데 중점을 둔다. $q(x_{t-1} \vert x_t, x_0)$과 $x_0$의 one-hot 표현에 대한 합계를 결합하여 다음과 같은 parameterization을 얻는다.
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) \propto \sum_{\tilde{x}_0} q(x_{t-1}, x_t \vert \tilde{x}_0) \tilde{p}_\theta (\tilde{x}_0 \vert x_t) \end{equation}\]이 $x_0$-parameterization에서 \(\tilde{p}_\theta (\tilde{x}_\theta \vert x_t)\)가 모든 확률 mass를 원래 값 $x_0$에 배치하는 경우 KL divergence
\[\begin{equation} D_\textrm{KL}[q(x_{t-1} \vert x_t, x_0) \;\|\; p_\theta (x_{t-1} \vert x_t)] = 0 \end{equation}\]이 된다. 주어진 상태 $x_t$에서 최적의 reverse process는 $q(x_t \vert x_{t-1})$이 0이 아닌 state로의 transition만을 고려한다. 따라서 $Q_t$의 sparsity 패턴은 $p_\theta (x_{t-1} \vert x_t)$에서 이상적인 reverse transition 확률의 sparsity 패턴을 결정한다. 위의 parameterization은 학습된 reverse 확률 분포 $p_\theta (x_{t-1} \vert x_t)$가 Markov transition 행렬 $Q_t$의 선택에 의해 지시된 올바른 sparsity 패턴을 갖도록 자동으로 보장한다. 이 parameterization을 통해
\[\begin{equation} p_\theta (x_{t-k} \vert x_t) = \sum q (x_{t−k}, x_t \vert \tilde{x}_0) \tilde{p}_\theta ( \tilde{x}_0 \vert x_t) \end{equation}\]를 예측하여 한 번에 $k$ step으로 inference를 수행할 수 있다.
마지막으로 순서형 이산 데이터를 모델링할 때 신경망의 출력으로 직접 \(\tilde{p}_\theta (\tilde{x}_0 \vert x_t)\)의 로짓을 예측하는 대신 또 다른 옵션은 discretize된 로지스틱 분포로 확률을 모델링하는 것이다. 이는 reverse model에 추가적인 순서형 inductive bias를 제공하고 이미지에 대한 FID와 log-likelihood 점수를 높인다.
4. Loss function
최근 연구에서 영감을 받아 각 timestep에서 데이터 $x_0$의 좋은 예측을 장려하는 reverse process의 $x_0$-parameterization을 위한 보조 denoising 목적 함수를 도입한다. 이를 VLB와 결합하여 다음과 같은 loss function을 생성한다.
\[\begin{equation} L_\lambda = L_\textrm{vb} + \lambda \mathbb{E}_{q (x_0)} \mathbb{E}_{q (x_t \vert x_0)} [-\log \tilde{p}_\theta (x_0 \vert x_t)] \end{equation}\]보조 loss는 $t = 1$에서 cross-entropy 항 $L_0$와 일치한다. 또한 $p_\theta (x_{t-1} \vert x_t)$의 $x_0$-parameterization으로 인해 정확히 \(\tilde{p}_\theta (\tilde{x}_0 \vert x_t)\)가 $x_0$에 모든 mass를 가질 때 보조 loss 항과 VLB의 $D_\textrm{KL}$이 모두 최소화된다. 저자들은 이 loss를 사용한 학습이 이미지 샘플의 품질 향상으로 이어진다는 것을 발견했다.
Connection to existing probabilistic models for text
D3PM 프레임워크와 기존의 여러 언어 모델링 접근 방식 사이에는 흥미로운 관계가 있다.
BERT is a one-step diffusion model
가능한 D3PM transition 행렬의 하나는 uniform transition 행렬과 [MASK] 토큰의 absorbing state의 조합이다.
\[\begin{equation} Q = \alpha 𝟙 e_m^\top + (\beta / K) 𝟙𝟙^\top + (1 - \alpha - \beta) I \end{equation}\]여기서 $e_m$은 [MASK] 토큰에서의 one-hot 벡터이다. $q(x_1 \vert x_0)$가 토큰의 10%를 [MASK]로 대체하고 5%를 무작위로 균일하게 대체하는 1단계 diffusion process의 경우 이는 정확하게 BERT denoising 목적 함수, 즉
\[\begin{equation} L_\textrm{vb} - L_T = - \mathbb{E}_{q(x_1 \vert x_0)} [\log p_\theta (x_0 \vert x_1)] = L_\textrm{BERT} \end{equation}\]이다.
Autoregressive models are (discrete) diffusion models
길이 $N = T$의 시퀀스로 토큰을 하나씩 deterministic하게 마스킹하는 diffusion process를 고려해보자.
\[\begin{equation} q([x_t]_i \vert x_0) = [x_0]_i \quad \textrm{if} \; i < N - t \; \textrm{ else [MASK]} \end{equation}\]이것은 deterministic forward process이므로 $q(x_{t-1} \vert x_t, x_0)$은 더 적은 마스크의 $x_t$ 시퀀스에 대한 델타 분포다.
\[\begin{equation} q([x_{t-1}]_i \vert x_t, x_0) = \delta_{[x_t]_i} \quad \textrm{if} \; i \ne T - t \; \textrm{else} \; \delta_{[x_0]_i} \end{equation}\]이 프로세스는 각 토큰에 독립적으로 적용되지 않지만 product space $[0 \cdots N] \times \mathcal{V}$에서 독립적으로 적용되는 diffusion process로 재구성할 수 있다. 여기서 각 토큰은 시퀀스에서 해당 위치로 태깅되고 $\mathcal{V}$는 vocabulary이며 $Q$는 $N \times \vert \mathcal{V} \vert \times N \times \vert \mathcal{V} \vert$ sparsity 행렬이다.
위치 $i = T - t$에 있는 토큰을 제외한 모든 토큰은 deterministic posterior를 가지므로 KL divergence
\[\begin{equation} D_\textrm{KL} (q([x_{t-1}]_j \vert x_t, x_0) \| p_\theta ([x_{t-1}]_j \vert x_t)) \end{equation}\]는 다른 모든 위치에 대해 0이다. 이것이 사실이 아닌 유일한 토큰은 위치 $i$에 있는 토큰이며 이는 autoregressive model의 표준 cross entropy loss이다.
\[\begin{equation} D_\textrm{KL} (q([x_{t-1}]_i \vert x_t, x_0) \| p_\theta ([x_{t-1}]_i \vert x_t)) = -\log p_\theta ([x_0]_i \vert x_t) \end{equation}\](Generative) Masked Language-Models (MLMs) are diffusion models
Generative Masked Language Model은 일련의 토큰에서 텍스트를 생성하는 생성 모델이다. 일반적으로 시퀀스 $x_0$을 샘플링하고 일부 schedule에 따라 $k$개의 토큰을 마스킹하고 주어진 컨텍스트에서 마스킹된 토큰을 예측하는 방법을 학습한다. $x_0$-parameterization을 사용하여 일반적인 ELBO 목적 함수에 대해 학습된 D3PM absorbing ([MASK]) model이 이 MLM 목적 함수의 재가중 버전으로 축소된다.
Text generation
1. Character-level generation on text8
다음은 text8에서의 문자 레벨 택스트 생성 결과이다.
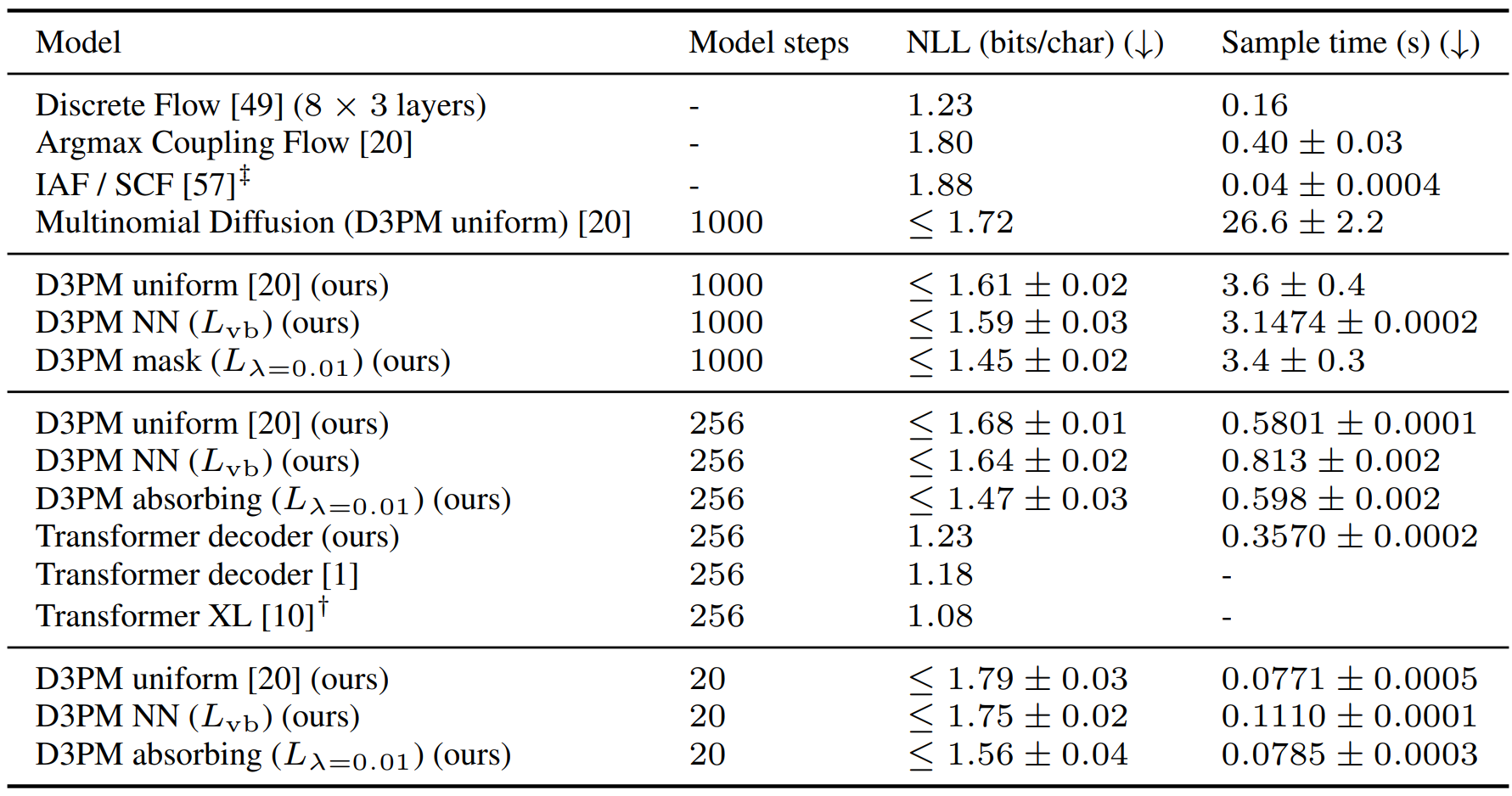
2. Text generation on LM1B
다음은 LM1B에서의 텍스트 생성 결과이다.
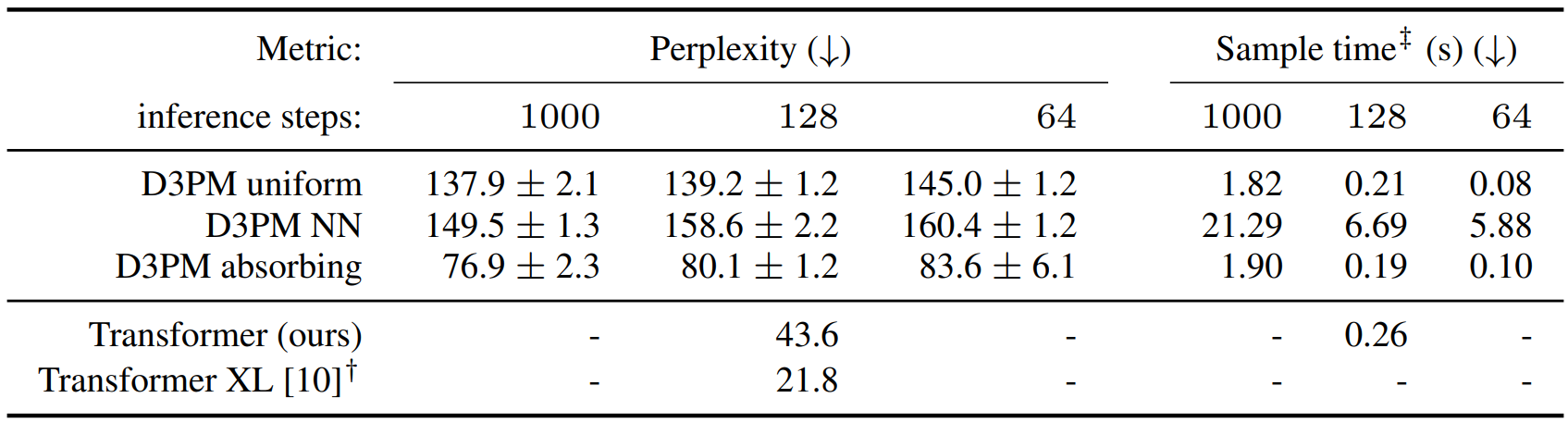
다음은 LM1B에서 샘플링 iteration에 대한 perplexity를 측정한 그래프이다.
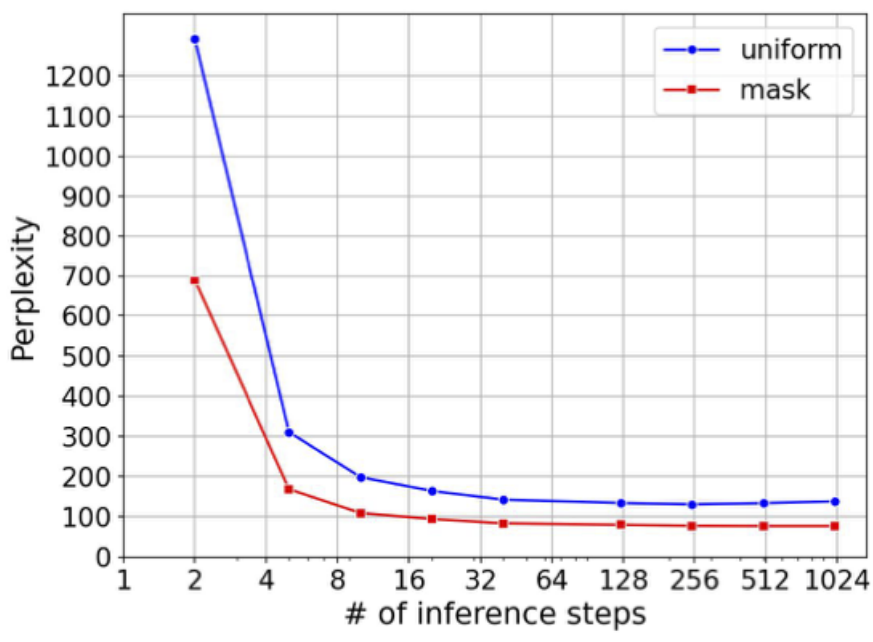
다음은 학습된 D3PM absorbing model로 생성한 새로운 문장(위)과 재구성한 손상된 문장(아래)이다.

Image generation
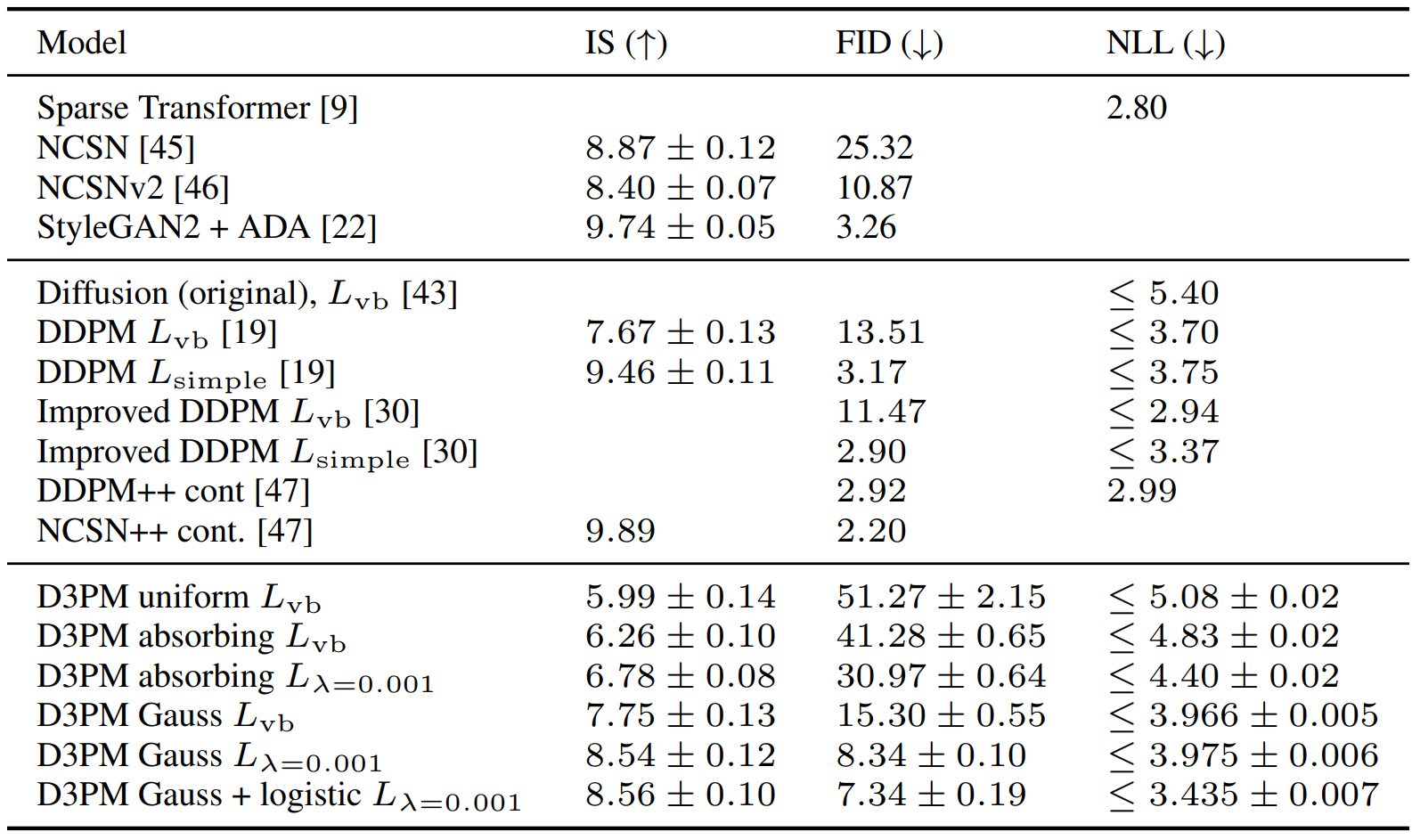
다음은 CIFAR-10에서 측정한 IS, FID, NLL이다.
다음은 D3PM absorbing model(위)과 D3PM Gauss + logistic model(아래)의 샘플링 예시이다. (cherry picked)

다음은 D3PM Gauss + logistic model의 샘플들이다. (non cherry picked)
