[논문리뷰] Zero-1-to-3: Zero-shot One Image to 3D Object
ICCV 2023. [Paper] [Page] [Github]
Ruoshi Liu, Rundi Wu, Basile Van Hoorick, Pavel Tokmakov, Sergey Zakharov, Carl Vondrick
Columbia University | Toyota Research Institute
20 Mar 2023
Introduction
단 하나의 카메라 view에서 인간은 물체의 3D 모양과 외형을 상상할 수 있다. 이 능력은 복잡한 환경에서의 개체 조작 및 탐색과 같은 일상적인 작업에 중요하지만 그림과 같은 시각적 창의성에도 중요하다. 이 능력은 대칭과 같은 기하학적 prior에 의존하여 부분적으로 설명할 수 있지만 물리적 및 기하학적 제약을 쉽게 깨는 훨씬 더 어려운 객체로 일반화할 수 있다. 실제로 물리적 세계에 존재하지 않는 (또는 존재하지 않는) 객체의 3D 모양을 예측할 수 있다. 이 정도의 일반화를 달성하기 위해 인간은 평생 시각적 탐색을 통해 축적된 사전 지식 (prior)에 의존한다.
대조적으로, 3D 이미지 재구성을 위한 대부분의 기존 접근 방식은 값비싼 3D 주석 (ex. CAD 모델) 또는 카테고리별 prior에 의존하기 때문에 closed-world setting에서 작동한다. 최근 몇 가지 방법이 CO3D와 같은 대규모의 다양한 데이터셋에 대한 사전 학습을 통해 open world 3D 재구성 방향으로 큰 발전을 이루었다. 그러나 이러한 접근 방식에는 여전히 stereo view 또는 카메라 포즈와 같은 학습용 기하학 관련 정보가 필요한 경우가 많다. 결과적으로 그들이 사용하는 데이터의 규모와 다양성은 대규모 diffusion model의 성공을 가능하게 하는 최근의 인터넷 규모의 텍스트-이미지 수집과 비교할 때 미미한 수준으로 남아 있다. 인터넷 규모의 사전 학습은 이러한 모델에 풍부한 semantic prior을 부여하는 것으로 나타났지만 기하학적 정보를 캡처하는 정도는 아직 많이 연구되지 않은 상태로 남아 있다.
본 논문에서는 zero-shot 새로운 view 합성과 3D 형상 재구성을 수행하기 위해 Stable Diffusion과 같은 대규모 diffusion model에서 카메라 시점을 조작하는 컨트롤 메커니즘을 학습할 수 있음을 보었다. 단일 RGB 이미지가 주어지면 이 두 task 모두 제약이 매우 적다. 그러나 최신 생성 모델에서 사용할 수 있는 학습 데이터의 규모 (50억 개 이상의 이미지)로 인해 diffusion model은 자연스러운 이미지 분포를 위한 SOTA 표현이며 다양한 시점에서 방대한 수의 객체를 지원한다. 카메라 대응 없이 2D 단안 이미지에 대해 학습을 받았지만 생성 프로세스 중에 상대적인 카메라 rotation과 translation에 대한 컨트롤을 학습하도록 모델을 fine-tuning할 수 있다. 이러한 컨트롤을 사용하면 선택한 다른 카메라 시점으로 디코딩되는 임의의 이미지를 인코딩할 수 있다.
Method
객체의 단일 RGB 이미지 $x \in \mathbb{R}^{H \times W \times 3}$이 주어지면 본 논문의 목표는 다른 카메라 시점에서 객체의 이미지를 합성하는 것이다. $R \in \mathbb{R}^{3 \times 3}$과 $T \in \mathbb{R}^3$을 각각 원하는 시점의 상대적인 카메라 rotation과 translation이라고 하자. 본 논문은 이 카메라 변환에서 새로운 이미지를 합성하는 모델 $f$를 학습하는 것을 목표로 한다.
\[\begin{equation} \hat{x}_{R, T} = f(x, R, T) \end{equation}\]여기서 \(\hat{x}_{R, T}\)를 합성된 이미지로 나타낸다. 추정된 \(\hat{x}_{R, T}\)가 참이지만 관찰되지 않은 새로운 view $x_{R,T}$와 지각적으로 유사하기를 원한다.
단안 RGB 이미지로부터의 새로운 view 합성은 심하게 제한되어 있다. 본 논문의 접근 방식은 이 task를 수행하기 위해 Stable Diffusion과 같은 대규모 diffusion model을 활용한다. 텍스트 설명에서 다양한 이미지를 생성할 때 탁월한 zero-shot 능력을 보여주기 때문이다. 학습 데이터의 규모로 인해 사전 학습된 diffusion model은 오늘날 자연스러운 이미지 분포를 위한 SOTA 표현이다.
그러나 $f$를 만들기 위해 극복해야 할 두 가지 과제가 있다. 첫째, 대규모 생성 모델이 서로 다른 관점에서 다양한 객체에 대해 학습되지만 표현은 시점 간의 대응 관계를 명시적으로 인코딩하지 않는다. 둘째, 생성 모델은 인터넷에 반영된 시점 편향을 물려받는다.

위 그림에서 볼 수 있듯이 Stable Diffusion은 정면을 향한 의자의 표준 포즈 이미지를 생성하는 경향이 있다. 이 두 가지 문제는 대규모 diffusion model에서 3D 지식을 추출하는 능력을 크게 방해한다.
1. Learning to Control Camera Viewpoint
Diffusion model은 인터넷 규모 데이터에 대해 학습되었기 때문에 자연스러운 이미지 분포에 대한 지원은 대부분의 개체에 대한 대부분의 시점을 커버할 가능성이 높지만 이러한 시점은 사전 학습된 모델에서 제어할 수 없다. 사진을 캡처하는 데 사용되는 카메라 extrinsic을 제어하는 메커니즘을 모델에 가르칠 수 있으면 새로운 view 합성을 수행하는 능력을 가질 수 있다.
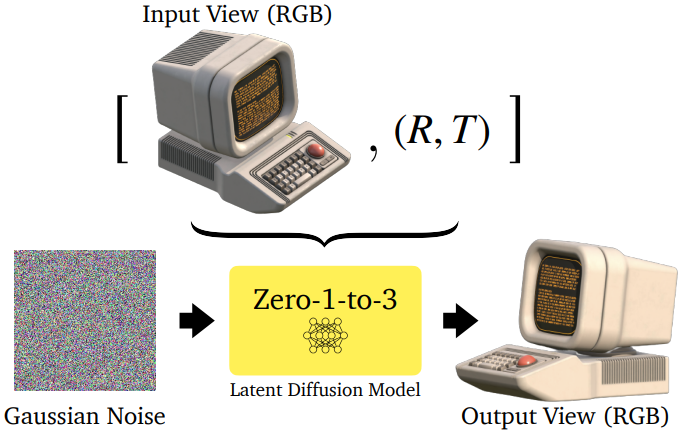
이를 위해 위 그림에 표시된 한 쌍의 이미지와 관련 카메라 extrinsic \(\{ (x, x_{(R,T)}, R, T) \}\)의 데이터셋이 주어지면 사전 학습된 diffusion model을 순서대로 fine-tuning한다. 나머지 표현을 파괴하지 않고 카메라 파라미터에 대한 컨트롤을 학습한다. 인코더 $\mathcal{E}$, denoiser U-Net $\epsilon_\theta$, 디코더 $\mathcal{D}$를 가지는 latent diffusion 아키텍처를 사용한다. Timestep $t \sim [1, 1000]$에서 $c(x, R, T)$를 입력 view와 상대적인 카메라 extrinsic의 임베딩이라 하자. 그러면 모델을 fine-tuning하기 위해 다음 목적 함수를 해결한다.
모델 $\epsilon_\theta$가 학습된 후, inference 모델 $f$는 $c(x, R, T)$을 조건으로 Gaussian noise 이미지에서 반복적인 denoising을 수행하여 이미지를 생성할 수 있다.
본 논문의 주요 결과는 사전 학습된 diffusion model을 이러한 방식으로 fine-tuning하면 카메라 시점을 제어하기 위한 일반적인 메커니즘을 학습할 수 있다는 것이다. 다시 말해, 이 fine-tuning을 통해 컨트롤을 통합할 수 있으며 diffusion model은 시점 제어가 있는 경우를 제외하고 사실적인 이미지를 생성하는 능력을 유지할 수 있다. 이 compositionality (합성성)는 모델에 zero-shot 능력을 부여하며, 최종 모델이 3D 에셋이 부족하고 fine-tuning 세트에 나타나지 않는 개체 클래스에 대한 새로운 view를 합성할 수 있도록 한다.
2. View-Conditioned Diffusion
단일 이미지에서 3D 재구성하려면 낮은 레벨의 인식 (깊이, 음영, 질감 등)과 높은 레벨의 이해 (유형, 기능, 구조 등)가 모두 필요하다. 따라서 하이브리드 컨디셔닝 메커니즘을 채택한다. 하나의 스트림에서 입력 이미지의 CLIP 임베딩은 $(R, T)$와 concat되어 $c(x, R, T)$를 임베딩하는 “posed CLIP”을 형성한다. Cross-attention을 적용하여 입력 이미지의 높은 레벨의 semantic 정보를 제공하는 denoising U-Net을 컨디셔닝한다. 다른 스트림에서 입력 이미지는 denoise되는 이미지와 채널 차원으로 concat되어 모델이 합성되는 개체의 ID와 디테일을 유지하는 데 도움이 된다. Classifier-free guidance를 적용할 수 있도록 InstructPix2Pix에서 제안된 유사한 메커니즘을 따라 입력 이미지와 포즈를 취한 CLIP 임베딩을 null 벡터로 랜덤하게 설정하고 inference 중에 조건부 정보를 스케일링한다.
3. 3D Reconstruction
많은 애플리케이션에서 개체의 새로운 view를 합성하는 것만으로는 충분하지 않다. 개체의 모양과 형상을 모두 캡처하는 완전한 3D 재구성이 필요하다. 저자들은 최근 오픈 소스 프레임워크인 Score Jacobian Chaining (SJC)를 채택하여 text-to-image diffusion model의 prior로 3D 표현을 최적화한다. 그러나 diffusion model의 확률적 특성으로 인해 기울기 업데이트는 매우 확률적이다. DreamFusion에서 영감을 얻은 SJC에서 사용되는 중요한 기술은 classifier-free guidance 값을 평소보다 훨씬 높게 설정하는 것이다. 이 방법론은 각 샘플의 다양성을 감소시키지만 재구성의 충실도를 향상시킨다.
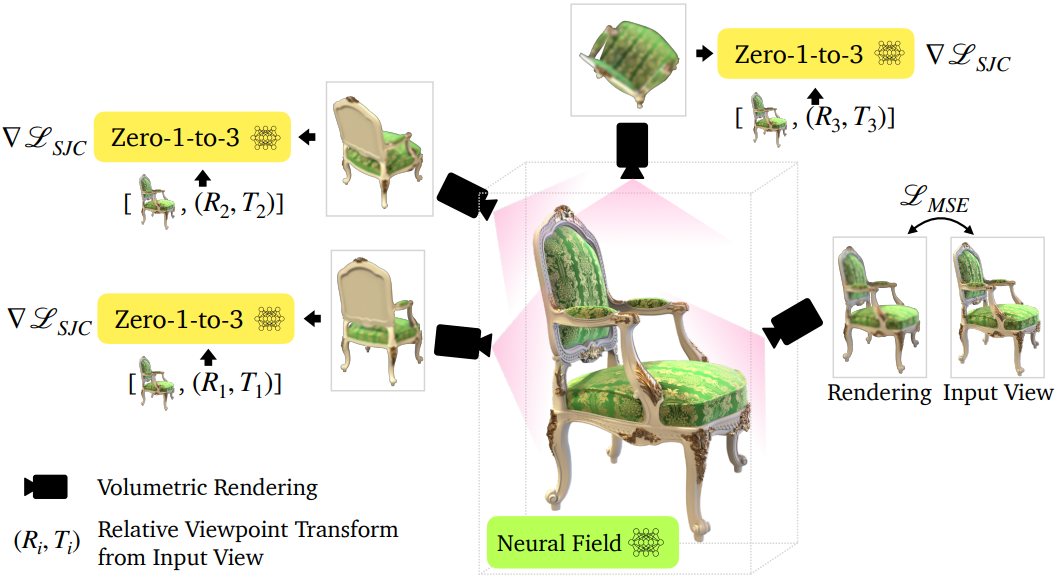
위 그림에서 볼 수 있듯이 SJC와 유사하게 시점을 랜덤으로 샘플링하고 체적 렌더링을 수행한다. 그런 다음 결과 이미지를 Gaussian noise $\epsilon \sim \mathcal{N} (0,I)$로 섭동시키고, noisy하지 않은 입력 $x_\pi$에 대한 score를 근사화하기 위해 입력 이미지 $x$, posed CLIP 임베딩 $c(x, R, T)$, timestep $t$로 컨디셔닝된 U-Net $\epsilon_\theta$를 적용하여 denoise한다.
여기서 \(\nabla \mathcal{L}_\textrm{SJC}\)는 SJC에서 도입된 PAAS score이다.
또한 MSE loss로 입력 view를 최적화한다. NeRF 표현을 더욱 정규화하기 위해 샘플링된 모든 시점에 depth smoothness loss를 적용하고 near-view consistency loss를 적용하여 주변 view 사이의 모양 변화를 정규화한다.
4. Dataset
본 논문은 10만 명 이상의 아티스트가 만든 80만 개 이상의 3D 모델을 포함하는 최근에 출시된 대규모 오픈 소스 데이터셋인 Objaverse 데이터셋을를 fine-tuning에 사용한다. ShapeNet과 같은 명시적인 클래스 레이블은 없지만 Objaverse는 풍부한 형상을 가진 다양한 고품질 3D 모델을 구현하며 그 중 많은 부분이 세밀한 디테일과 재료 속성을 가지고 있다. 데이터셋의 각 개체에 대해 개체의 중심을 가리키는 12개의 카메라 extrinsics matrix $\mathcal{M}$을 무작위로 샘플링하고 레이트레이싱 엔진으로 12개의 view를 렌더링한다. 학습 시 각 개체에 대해 두 개의 view를 샘플링하여 이미지 쌍 $(x, x_{R,T})$를 형성할 수 있다. 두 시점 사이의 매핑을 정의하는 상대적인 시점 변환 $(R, T)$는 두 개의 extrinsic matrix에서 쉽게 파생될 수 있다.
Experiments
1. Novel View Synthesis Results
다음은 Google Scanned Objects에 대한 새로운 view 합성 결과이다.


다음은 RTMV에 대한 새로운 view 합성 결과이다.

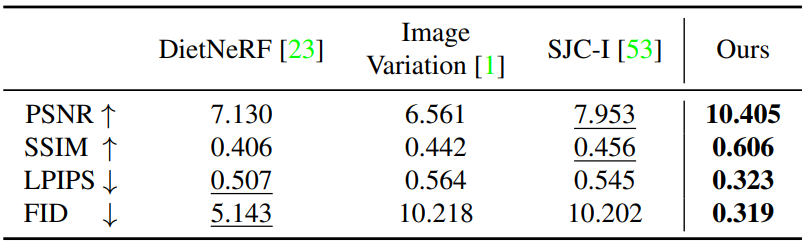
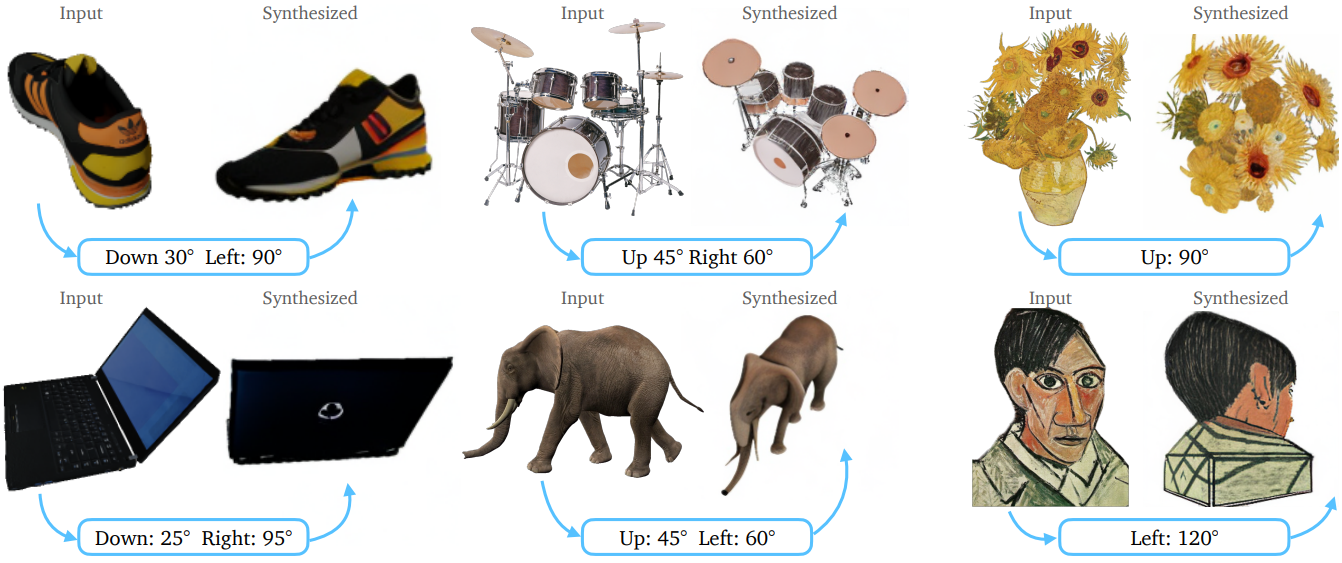
다음은 실제 이미지에 대한 새로운 view 합성 결과이다.

다음은 새로운 view 합성의 다양성을 나타낸 것이다.

2. 3D Reconstruction Results
다음은 Google Scanned Objects에 대한 단일 view 3D 재구성 결과이다.

다음은 RTMV에 대한 단일 view 3D 재구성 결과이다.
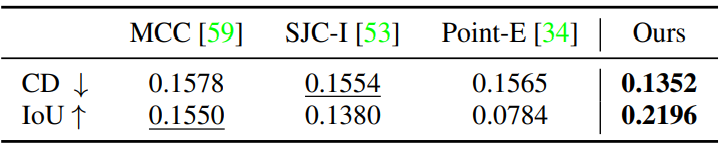
다음은 3D 재구성의 정성적 예시이다.

3. Text to Image to 3D
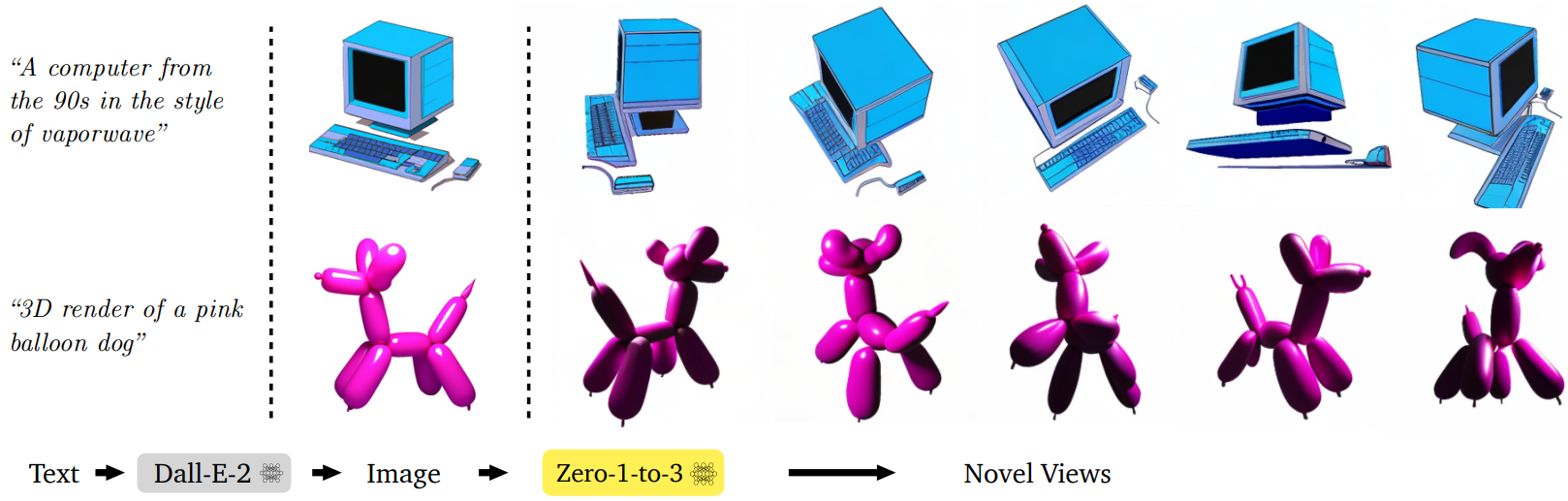
다음은 Dall-E-2로 생성된 이미지에 대한 새로운 view 합성 결과이다.