[논문리뷰] WildGaussians: 3D Gaussian Splatting in the Wild
NeurIPS 2024. [Paper] [Page] [Github]
Jonas Kulhanek, Songyou Peng, Zuzana Kukelova, Marc Pollefeys, Torsten Sattler
CTU in Prague | ETH Zurich
11 Jul 2024

Introduction
학습 뷰에서만 장면 표현을 학습하면 형상과 view-dependent한 효과 사이에 모호성이 발생한다. NeRF와 3DGS는 일관된 조명과 장면을 가리는 물체가 거의 없는 제어된 설정에서는 잘 작동하지만 일반적으로 다양한 조건과 가리는 부분이 큰 경우에서는 실패한다. 그러나 실제로는 환경을 제어하지 않고 이미지를 캡처한다. 환경 조건 변화 (ex. 낮과 밤의 변화) 외에도 이러한 이미지에는 일반적으로 자동차와 같은 장면을 가리는 물체가 포함되어 있으며, 재구성 프로세스 중에 이를 처리해야 한다.
본 논문은 문제를 해결하기 위해 학습 가능한 외형 임베딩으로 Gaussian을 향상시키고 작은 MLP를 사용하여 이미지와 외형 임베딩을 통합하여 기본 색상의 affine transformation을 예측하였다. 이 MLP는 학습 중이나 새 이미지의 외형을 캡처할 때만 필요하다. 이 단계 후에 외형을 표준 3DGS로 다시 베이킹하여 3DGS 표현의 편집 가능성과 유연성을 유지하면서 빠른 렌더링을 보장한다. 장면을 가리는 물체들을 robust하게 처리하기 위해 DINOv2 feature에 기반한 loss를 갖는 불확실성 예측기를 도입하여 학습 중에 이러한 물체들을 효과적으로 제거한다.
Method
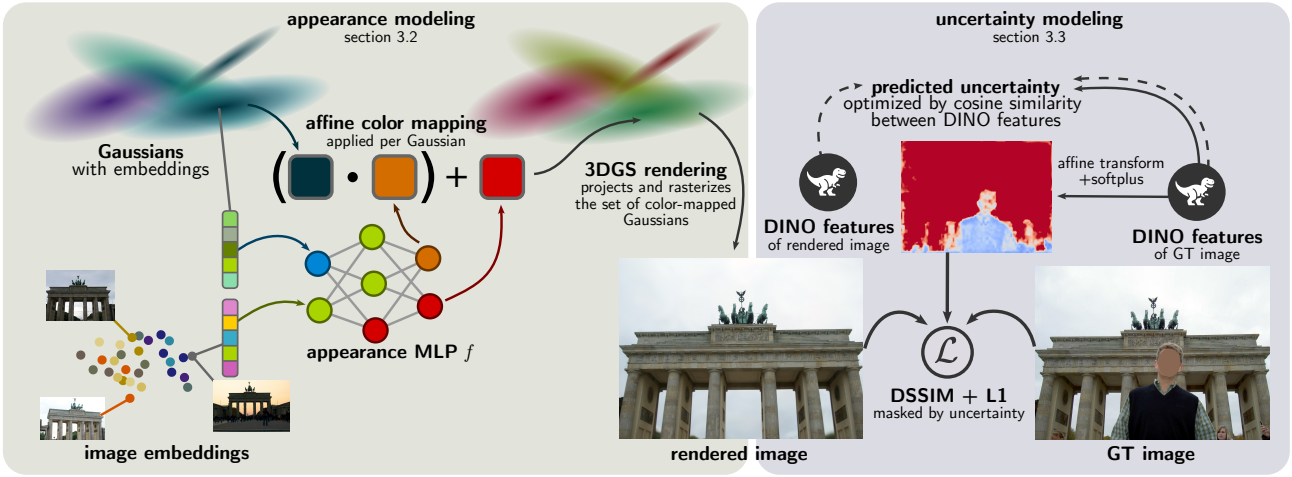
본 논문은 3DGS 기반 접근 방식이 제어되지 않는 장면 캡처를 처리할 수 있도록 하기 위해 두 가지 핵심 구성 요소를 제안하였다.
- 외형 모델링을 통해 관찰된 픽셀 색상이 시점뿐만 아니라 캡처 시간이나 날씨와 같은 조건에 따라 달라진다는 사실을 처리할 수 있다. 이러한 조건을 모델링하기 위해 학습 이미지별로 외형 임베딩을 학습시킨다. 또한 로컬한 효과를 모델링하기 위해 Gaussian별 외형 임베딩을 학습시킨다. 두 임베딩을 MLP에 입력하여 color space에서의 affine mapping을 예측한다.
- 불확실성 모델링은 학습 이미지의 어떤 영역을 무시해야 하는지 결정함으로써 학습 단계에서 가리는 물체를 처리할 수 있게 해준다. 이를 위해, 학습 이미지에서 DINOv2 feature를 추출하고, 이를 학습 가능한 affine transformation에 입력으로 전달하는데, 이는 픽셀별 불확실성을 예측하고, 이미지의 어떤 부분이 정적 영역에 해당할 가능성이 높고 어떤 부분이 가리는 물체에 해당하는 지를 인코딩한다. 불확실성 예측기는 학습 이미지와 렌더링에서 추출한 DINO feature 간의 cosine similarity를 사용하여 최적화된다.
1. Appearance Modeling
다양한 외형과 조명을 가진 이미지를 처리하기 위해 학습 가능한 per-image embedding \(\{\mathbf{e}_j\}_{j=1}^N\)을 사용한다 ($N$은 학습 이미지의 수). 또한, 다양한 외형에서 다양한 색상의 Gaussian을 사용할 수 있도록 각 Gaussian $i$에 대해 학습 가능한 per-Gaussian embedding \(\mathbf{g}_i\)를 포함한다. \(\mathbf{e}_j\), \(\mathbf{g}_i\), 기본 색상 \(\bar{c}_i\) (0-th order SH)를 MLP $f$에 입력한다.
\[\begin{equation} (\beta, \gamma) = f (\mathbf{e}_j, \mathbf{g}_i, \bar{c}_i) \end{equation}\]출력은 affine transformation의 파라미터이며, \((\beta, \gamma) = \{(\beta_k, \gamma_k)\}_{k=1}^3\)는 각 색상 채널 $k$에 대해 적용된다. $i$번째 Gaussian의 toning된 색상 \(\tilde{c}_i\)는 다음과 같다.
\[\begin{equation} \tilde{c}_i = \gamma \cdot \hat{c}_i (\mathbf{r}) + \beta \end{equation}\](\(\hat{c}_i (\mathbf{r})\)는 광선 방향 $\mathbf{r}$에 대한 $i$번째 Gaussian의 색상)
그런 다음 이러한 Gaussian 색상은 3DGS rasterization 프로세스에 대한 입력으로 사용된다. Per-image embedding \(\mathbf{e}_j\)만 사용하는 기존 방법들과 달리, 본 논문은 광원에 의해 변하는 장면의 일부와 같은 로컬한 변화를 모델링하기 위해 per-Gaussian embedding \(\mathbf{g}_i\)를 함께 사용한다.
테스트 시에 렌더링 속도가 중요하고 장면을 하나의 정적 조건에서만 렌더링해야 하는 경우, affine 파라미터를 Gaussian별로 미리 계산하여 Gaussian의 SH 파라미터를 업데이트하는 데 사용할 수 있다.
Per-Gaussian Emeddings \(\mathbf{g}_i\) 초기화
임베딩 \(\mathbf{g}_i\)를 무작위로 초기화하면 locality bias가 부족하여 일반화 및 학습 성능이 떨어질 수 있다. 대신, locality prior를 적용하기 위해 Fourier feature를 사용하여 초기화한다.
구체적으로, 먼저 $L^\infty$ norm의 97% 백분위수를 사용하여 입력 포인트 클라우드를 범위로 중앙에 배치하고 정규화한다. 그런 다음 정규화된 포인트 $p$의 Fourier feature는 $\sin (\pi p_k 2^m)$과 $\cos (\pi p_k 2^m)$를 concat하여 얻는다. 여기서 $k = 1, 2, 3$은 좌표 인덱스이고 $m = 1, \ldots, 4$이다.
목적 함수
3DGS는 DSSIM loss와 L1 loss를 조합하여 학습에 사용하지만, 본 논문에서는 DSSIM과 L1은 다른 목적으로 사용된다. DSSIM의 경우 L1보다 외형 변화에 더 robust하고 구조적 유사성에 더 중점을 두므로 외형 모델링을 적용하지 않은 렌더링 이미지에 사용한다. 반면에 L1 loss는 올바른 외형 모델링을 적용한 렌더링 이미지에 사용된다. 학습 loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{color} = \lambda_\textrm{dssim} \textrm{DSSIM} (\hat{C}, C) + (1 - \lambda_\textrm{dssim}) \| \tilde{C} - C \|_1 \end{equation}\]($C$는 GT 이미지, $\hat{C}$와 $\tilde{C}$는 각각 color toning 전후의 렌더링 이미지)
Per-Image Embeddings \(\mathbf{e}_j\)의 test-time 최적화
학습하는 동안, 3DGS 표현과 MLP와 함께 \(\mathbf{e}_j\)와 \(\mathbf{g}_i\)를 공동으로 최적화한다. 그러나 이전에 보지 못한 이미지의 외형을 맞추려면 보지 못한 이미지의 임베딩에 대한 test-time 최적화를 수행해야 한다. 이를 위해 이미지의 외형 벡터를 0으로 초기화하고 나머지는 모두 고정한 채 Adam optimizer를 사용하여 \(\mathcal{L}_\textrm{color}\)로 최적화한다.
2. Uncertainty Modeling for Dynamic Masking
일시적인 물체와 가리는 물체가 학습 프로세스에 미치는 영향을 줄이기 위해 불확실성 모델을 학습시킨다. NeRF On-the-go는 사전 학습된 DINOv2의 feature를 사용하면 불확실성 예측기의 robustness가 높아진다는 것을 보여주었다. 그러나 통제된 설정에서는 잘 작동하지만 불확실성 loss function은 강한 외형 변화를 처리할 수 없다.
따라서 저자들은 외형 변화에 더 robust한 새로운 불확실성 loss를 제안하였다.
- 각 학습 이미지 $j$에 대해 먼저 DINOv2 feature를 추출한다.
- DINOv2 feature에 학습 가능한 affine mapping을 적용한 다음 softplus activation function를 적용하여 불확실성을 예측한다.
- Feature들은 패치 단위 (14$\times$14)이므로, 얻은 불확실성에 bilinear interpolation을 사용하여 원래 크기로 업스케일한다.
- 불확실성을 $[0.1, \infty)$으로 clipping하여 각 픽셀에 최소한의 가중치가 지정되도록 한다.
불확실성 최적화
NeRF 연구들에서는 모델이 하나의 색상 값 대신 각 픽셀에 대해 Gaussian 분포를 출력하도록 함으로써 불확실성을 모델링한다. 각 픽셀에 대하여 $C$와 $\tilde{C}$를 GT 색상과 예측된 색상, $\sigma$를 예측된 불확실성이라 하자. Per-pixel loss function은 평균이 $\tilde{C}$이고 분산이 $\sigma$인 정규 분포의 negative log-likelihood이다.
\[\begin{equation} \mathcal{L}_u = - \log \bigg( \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \bigg( - \frac{\| \tilde{C} - C \|_2^2}{2 \sigma^2} \bigg) \bigg) = \frac{\| \tilde{C} - C \|_2^2}{2 \sigma^2} + \log \sigma + \frac{\log 2 \pi}{2} \end{equation}\]
NeRF On-the-go에서는 MSE를 약간 수정된 DSSIM으로 대체하였다. DSSIM은 MSE와 다른 분포를 가지고 있지만, 안정적인 학습으로 이어질 수 있다. 하지만, 위 그림에서 볼 수 있듯이 MSE와 DSSIM은 모두 외형 변화에 강하지 않다. 이로 인해 이러한 MSE 기반 및 SSIM 기반 방법은 외형이 다른 영역이 최적화 프로세스에서 무시되므로 올바른 외형을 학습할 수 없다.
따라서, 저자들은 외형 변화에 더 강인한 DINOv2 feature를 다시 한 번 활용하였다. 학습 이미지와 예측 이미지의 DINOv2 feature에 대한 cosine similarity를 사용하여 loss function을 구성할 수 있다. DINOv2 feature는 픽셀이 아니라 이미지 패치별로 정의되므로 패치별로 불확실성 loss를 계산한다. $\tilde{D}$와 $D$를 각각 예측된 이미지 패치와 학습 이미지 패치의 DINO feature라 하면, loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{dino} (\tilde{D}, D) = \min \bigg(1, 2 - \frac{2 \tilde{D} \cdot D}{\| \tilde{D} \|_2 \| D \|_2} \bigg) \end{equation}\]두 feature의 cosine similarity가 1인 경우 \(\mathcal{L}_\textrm{dino}\)가 0이 되고, cosine similarity가 1/2 아래로 떨어지면 \(\mathcal{L}_\textrm{dino}\)가 1이 된다.
마지막으로 불확실성을 최적화하기 위해 log prior를 추가하여 다음과 같은 per-patch loss를 얻는다.
\[\begin{equation} \mathcal{L}_\textrm{uncertainty} = \frac{\mathcal{L}_\textrm{dino} (\tilde{D}, D)}{2 \sigma^2} + \lambda_\textrm{prior} \log \sigma \end{equation}\]이 loss는 불확실성 예측기를 최적화하는 데만 사용되며, gradient가 렌더링 파이프라인을 통해 전파되지 않도록 한다. 또한 3DGS 학습 중에 불투명도는 주기적으로 작은 값으로 재설정되어 local minima를 방지한다. 그러나 불투명도를 재설정할 때마다 렌더링은 일시적으로 잘못된 불투명도로 인해 손상된다. 이 문제가 불확실성 예측기로 전파되는 것을 방지하기 위해 불투명도를 재설정할 때마다 일정 iteration 동안 불확실성 학습을 비활성화한다.
불확실성을 사용하여 3DGS 최적화
NeRF의 경우 불확실성을 사용하여 학습 loss에 직접 가중치를 적용할 수 있다. 저자들은 gradient의 절댓값이 densification 알고리즘에 사용되고 큰 scale이 과도한 성장으로 이어지기 때문에 안정적인 학습으로 이어지지 않는다는 것을 관찰했다. 불확실성 가중치는 hyperparameter의 올바른 선택에 민감하게 만든다.
따라서 이 문제를 처리하기 위해 불확실성 점수를 per-pixel binary mask로 변환하여 gradient scaling이 최대 1이 되도록 한다.
\[\begin{equation} M = \unicode{x1D7D9} \bigg( \frac{1}{2 \sigma^2} > 1 \bigg) \end{equation}\]이 마스크는 per-pixel loss에 곱해진다.
\[\begin{equation} \mathcal{L}_\textrm{color-masked} = \lambda_\textrm{dssim} M \textrm{DSSIM} (\hat{C}, C) + (1 - \lambda_\textrm{dssim}) M \| \tilde{C} - C \|_1 \end{equation}\]3. Handling Sky
다양한 조건에서 장면을 사실적으로 렌더링하려면 하늘을 모델링하는 것이 중요하다. Structure-from-Motion 포인트들을 초기화로 사용하면 하늘에 Gaussian이 생성될 가능성은 낮다. 따라서 3D 장면 주변의 구에서 3D 포인트를 샘플링하여 3D Gaussian을 초기화하는 데 추가로 사용한다. 구에서 3D 포인트들을 균등하게 분포시키기 위해 Fibonacci sphere sampling algorithm을 활용한다. 이러한 포인트들을 고정된 반지름 $r_s$에 있는 구에 배치한 후 모든 학습 카메라에 projection하여 어떤 카메라에서도 보이지 않는 점을 제거한다.
Experiments
- 데이터셋: NeRF On-the-go, Photo Tourism
1. Comparison
다음은 NeRF On-the-go 데이터셋에 대한 비교 결과이다.


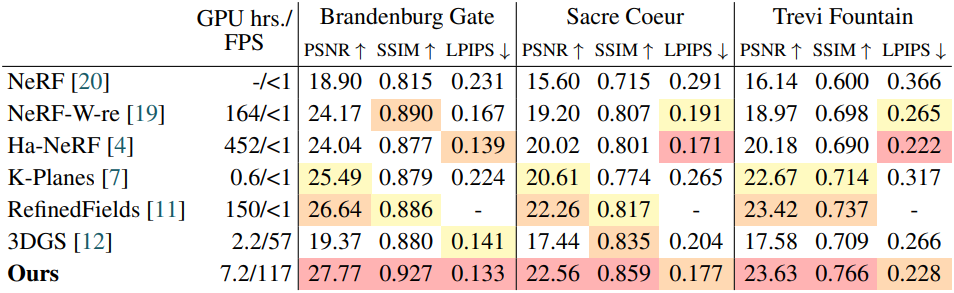
다음은 Photo Tourism 데이터셋에 대한 비교 결과이다.

2. Ablation Studies & Analysis
다음은 ablation 결과이다.

3. Analysis
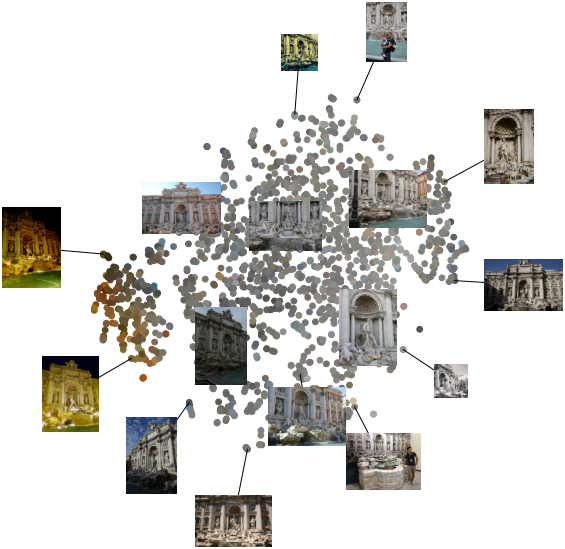
다음은 t-SNE로 외형 임베딩을 시각화한 것이다.

다음은 외형을 보간한 예시이다.
Limitations
- 조명이나 반사에 의해 생기는 물체의 하이라이트를 캡처할 수 없다.
- 불확실성 모델링이 MSE나 SSIM보다 더 강력하지만, 여전히 몇 가지 어려운 시나리오에서는 어려움을 겪는다.