[논문리뷰] WaveGrad: Estimating Gradients for Waveform Generation

ICLR 2021. [Paper] [Page] [Github]
Nanxin Chen, Yu Zhang, Heiga Zen, Ron J. Weiss, Mohammad Norouzi, William Chan
Center for Language and Speech Processing, Johns Hopkins University | Brain Team, Google Research
2 Sep 2020

Introduction

심층 생성 모델은 음성 합성에 혁명을 일으켰다. 특히 autoregressive model은 tractable한 likelihood, 간단한 inference 절차, 높은 fidelity의 샘플 덕분에 오디오 생성에 널리 사용되었다. 그러나 autoregressive model은 오디오 샘플을 생성하기 위해 많은 수의 순차적 계산이 필요하다. 이로 인해 특수 하드웨어를 사용하는 경우에도 실시간 생성보다 빠른 속도가 필수적인 실제 애플리케이션에 적용하기 어렵다.

Normalizing flow, GAN, energy score, VAE, 디지털 신호 처리와 음성 생성 메커니즘에서 영감을 얻은 모델 등 오디오 생성을 위한 non-autoregressive model에 대한 많은 연구가 있었다. 이러한 모델들은 더 적은 수의 순차 연산을 요구하여 inference 속도를 향상시키지만 autoregressive model보다 품질이 낮은 샘플을 생성한다.

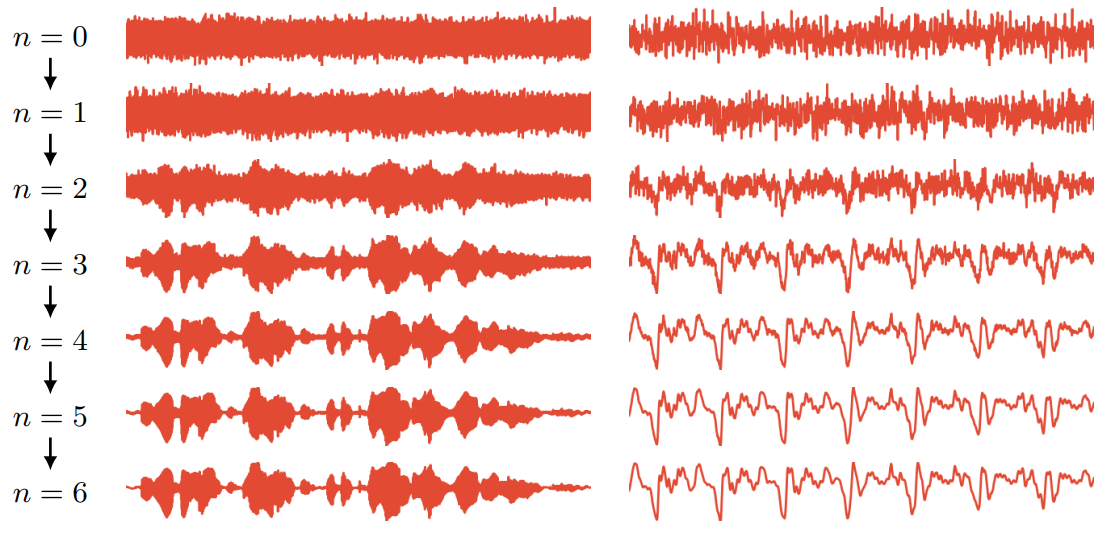
본 논문에서는 밀도 자체가 아닌 데이터 로그 밀도의 기울기를 추정하는 파형 샘플의 조건부 생성 모델인 WaveGrad를 소개한다. WaveGrad는 학습이 간단하고 log-lieklihood의 가중 variational lower-bound (VLB)를 암시적으로 최적화한다. WaveGrad는 autoregressive가 아니며 inference 중에 일정한 수의 생성 step만 필요하다. 위 그림은 WaveGrad의 inference 과정을 시각화한 것이다.

WaveGrad는 Stein score function이라고도 하는 데이터 로그 밀도의 기울기 학습을 통해 나타나는 생성 모델 클래스를 기반으로 한다. Inference하는 동안 데이터 로그 밀도의 기울기 추정에 의존하고 기울기 기반 sampler (ex. Langevin dynamics)를 사용하여 모델에서 샘플링할 수 있다. 밀접하게 관련된 것은 latent variable의 Markov chain을 통해 출력 분포를 캡처하는 diffusion probabilistic model이다. 이러한 모델은 tractable한 likelihood를 제공하지 않지만 log-likelihood에 대한 VLB를 최적화할 수 있다. 목적 함수는 deonising score matching과 유사하도록 reparameterize될 수 있으며 데이터 로그 밀도 기울기를 추정하는 것으로 해석될 수 있다. 이 모델은 inference 중에 autoregressive하지 않으며 Langevin dynamics-like sampler를 사용하여 Gaussian noise에서 시작하는 출력을 생성하는 일정한 수의 생성 step만 필요하다.

Estimating Gradients for Waveform Generation

Stein score function은 데이터 포인트 $y$에 대한 데이터 로그 밀도 $\log p(y)$의 기울기이다.

\[\begin{equation} s(y) = \nabla_y \log p(y) \end{equation}\]

Stein score function $s(\cdot)$가 주어지면 데이터 space에서 stochastic gradient ascent로 해석될 수 있는 Langevin dynamics를 통해 해당 밀도 $\tilde{y} \sim p(y)$에서 샘플을 그릴 수 있다.

\[\begin{equation} \tilde{y}_{i+1} = \tilde{y}_i + \frac{\eta}{2} s (\tilde{y}_i) + \sqrt{\eta} z_i \end{equation}\]

여기서 $\eta > 0$는 step size이고 $z_i \sim \mathcal{N}(0,I)$이다.

Inference를 위해 Langevin dynamics를 사용하여 Stein score function을 직접 학습하도록 신경망을 학습하여 생성 모델을 구축할 수 있다. Score matching으로 알려진 이 접근 방식은 이미지 및 모양 생성에서 성공을 거두었다. Denoising score matching 목적 함수는 다음과 같은 형식이다.

\[\begin{equation} \mathbb{E}_{y \sim p(y)} \mathbb{E}_{\tilde{y} \sim q(\tilde{y} \vert y)} [\| s_\theta (\tilde{y}) - \nabla_{\tilde{y}} \log q(\tilde{y} \vert y) \|_2^2] \end{equation}\]

여기서 $p(\cdot)$은 데이터 분포, $q(\cdot)$은 noise 분포이다.

최근 NCSN 논문에서 가중된 denoising score matching 목적 함수가 제안되었다.

\[\begin{equation} \sum_{\sigma \in S} \lambda (\sigma) \mathbb{E}_{y \sim p(y)} \mathbb{E}_{\tilde{y} \sim \mathcal{N}(y, \sigma)} \bigg[ \bigg\| s_\theta (\tilde{y}, \sigma) + \frac{\tilde{y} - y}{\sigma^2} \bigg\|_2^2 \bigg] \end{equation}\]

여기서 $S$는 데이터를 pertub하는 데 사용된 표준편차 값의 집합이며, $\lambda(\sigma)$는 다양한 $\sigma$에 대한 가중치 함수이다. WaveGrad는 이 접근 방식을 적용하여 조건부 생성 모델 $p(y \vert x)$를 학습한다. WaveGrad는 데이터 밀도의 기울기를 학습하며 inference이 경우 Langevin dynamics와 유사한 sampler를 사용한다.

Denoising score matching 프레임워크는 데이터 로그 밀도의 기울기를 학습하는 데 도움을 주는 noise 분포에 의존한다. Noise 분포로 무엇을 선택하는 지가 고품질의 샘플을 얻는데 중요한 영향을 준다.

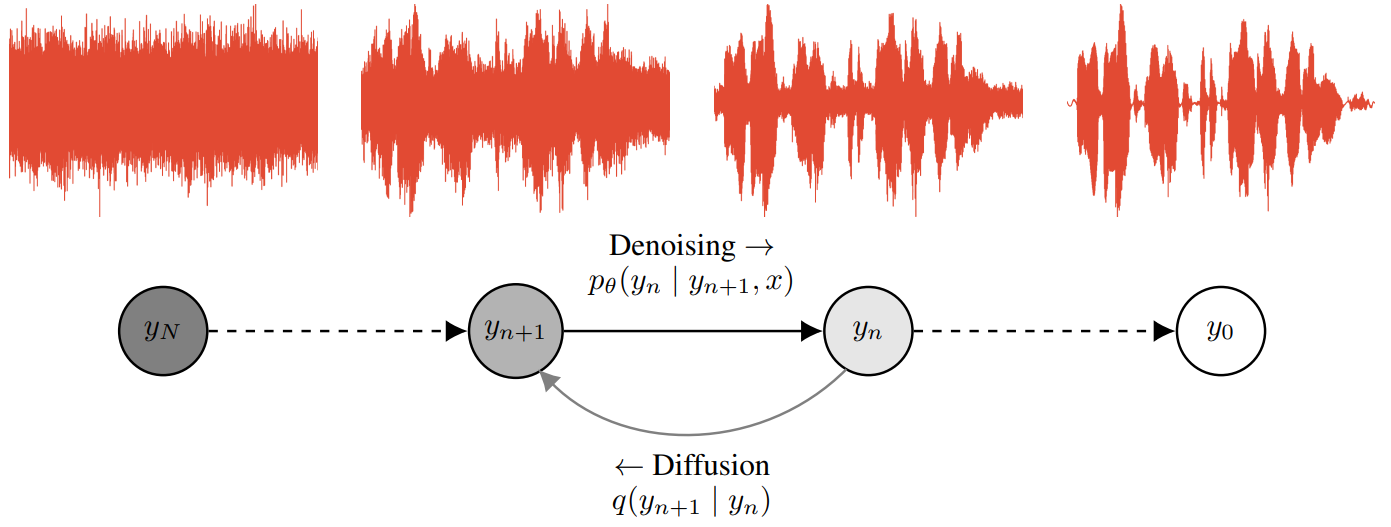
위 그림에서 볼 수 있듯이, WaveGrad는 diffusion model 프레임워크에 의존하여 score function을 학습하는 데 사용하는 noise 분포를 생성한다.

1. Wavegrad as a Diffusion Probabilistic Model

DDPM 논문에서는 diffusion probabilistic model과 score matching 목적 함수가 긴밀히 연관되어 있다는 것을 보였다. 따라서 diffusion probabilistic model로 WaveGrad를 먼저 도입한다.

Unconditional한 이미지 생성에서 조건부 오디오 파형 생성으로 DDPM의 diffusion model setup을 적용한다. WaveGrad는 조건부 분포 $p_\theta(y_0 \vert x)$를 모델링한다. 여기서 $y_0$는 파형이고 $x$는 해당 텍스트에서 파생된 언어 feature(y0에서 추출된 mel-spectrogram feature 또는 Tacotron 스타일의 TTS 모델로 예측된 acoustic features)이다.

\[\begin{equation} p_\theta (y_0 \vert x) := \int p_\theta (y_{0:N} \vert x) dy_{1:N} \end{equation}\]

여기서 $y_1, \cdots, y_N$은 일련의 latent variable이며, 각각은 데이터 $y_0$와 차원이 같다. 사후 확률 분포 $q(y_{1:N} \vert y_0)$는 diffusion process (또는 forward process)라 불리며 Markov chain으로 정의된다.

\[\begin{equation} q(y_{1:N} \vert y_0) := \prod_{n=1}^N q(y_n \vert y_{n-1}) \end{equation}\]

각 iteration은 noise schedule $\beta_1, \cdots, \beta_N$에 따라 Gaussian noise를 더한다.

\[\begin{equation} q(y_n \vert y_{n-1}) := \mathcal{N} (y_n; \sqrt{1 - \beta_n} y_{n-1}, \beta_n I) \end{equation}\]

임의의 step $n$에 대하여 diffusion process는 closed form으로 계산할 수 있다.

\[\begin{equation} y_n = \sqrt{\vphantom{1} \bar{\alpha}_n} y_0 + \sqrt{1 - \bar{\alpha}_n} \epsilon \\ \epsilon \sim \mathcal{N}(0,I), \quad \alpha_n := 1 - \beta_n, \quad \bar{\alpha}_n = \prod_{s=1}^n \alpha_s \end{equation}\]

Noise 분포의 기울기는

\[\begin{equation} \nabla_{y_n} \log q(y_n \vert y_0) = - \frac{\epsilon}{\sqrt{1 - \bar{\alpha}_n}} \end{equation}\]

이다. DDPM 논문에서는 $(y_0, y_n)$ 쌍으로 학습할 것을 제안하며 신경망을 모델 $\epsilon_\theta$로 reparameterize한다. 이 목적함수는 denoising score matching과 유사하다.

\[\begin{equation} \mathbb{E}_{n, \epsilon} [C_n \| \epsilon_\theta (\sqrt{\vphantom{1} \bar{\alpha}_n} y_0 + \sqrt{1 - \bar{\alpha}_n} \epsilon, x, n) - \epsilon \|_2^2] \end{equation}\]

여기서 $C_n$은 $\beta_n$에 연관된 상수이다. DDPM 논문에서는 $C_n$ 항을 제거하면 log-likelihood의 가중된 VLB가 되어 실제로 이점이 있다는 것을 발견하였다.

2. Noise Schedule and Conditioning on Noise Level

Score matching setup에서 NCSN 논문은 학습 중에 사용되는 noise 분포 선택의 중요성에 주목했으며, 이는 noise 분포가 기울기 분포 모델링을 지원하기 때문이다. Diffusion 프레임워크는 noise schedule이 $\beta_1, \cdots, \beta_n$으로 parameterize되는 score matching 지원을 제공하는 특정 접근 방식으로 볼 수 있다. 이것은 일반적으로 일부 hyperparameter heuristic을 통해 결정된다.

저자들은 특히 inference를 효율적으로 만들기 위해 inference 반복 횟수 $N$을 최소화하려고 할 때 높은 fidelity의 오디오를 달성하는 데 noise schedule의 선택이 중요하다는 것을 발견했다. 불필요한 noise가 포함된 schedule은 모델이 파형의 낮은 진폭 디테일을 복구할 수 없는 반면, 너무 적은 noise가 포함된 schedule은 inference 중에 제대로 수렴되지 않는 모델이 될 수 있다. NCSN 논문은 score matching 프레임워크에서 noise schedule 조정에 대한 통찰력을 제공하며, 이러한 통찰력 중 일부를 연결하고 diffusion 프레임워크에서 WaveGrad에 적용한다.

또 다른 문제는 diffusion/deonising step의 수인 $N$을 결정하는 것이다. 큰 $N$은 모델에 더 많은 계산 용량을 제공하고 샘플 품질을 향상시킬 수 있다. 그러나 작은 $N$을 사용하면 inference 속도가 빨라지고 계산 비용이 낮아진다. NCSN 논문은 32$\times$32 이미지를 생성하는 데 $N = 10$을 사용하였고, DDPM 논문은 256$\times$256 이미지를 생성하는 데 $N = 1000$을 사용하였다. WaveGrad의 경우 24kHz로 샘플링된 오디오를 생성한다.

저자들은 noise schedule과 $N$을 함께 조정하는 것이 특히 $N$이 작을 때 높은 fidelity의 오디오를 얻는 데 중요하다는 것을 발견했다. 이러한 hyperparameter가 제대로 조정되지 않으면 학습 샘플링 절차가 분포에 대한 지원이 부족할 수 있다. 결과적으로 inference 중에 샘플링 궤적이 학습 중에 표시된 조건에서 벗어난 영역을 만나면 sampler가 제대로 수렴되지 않을 수 있다. 그러나 많은 수의 모델을 학습하고 평가해야 하므로 검색 공간이 크기 때문에 이러한 hyperparameter를 조정하는 데 비용이 많이 들 수 있다.

WaveGrad 구현에서 위의 몇 가지 문제를 해결한다. 첫째, DDPM의 diffusion probabilistic model과 비교하여 불연속 iteration 인덱스 $n$ 대신 연속적인 noise level $\alpha$에 대하여 컨디셔닝하도록 모델을 reparameterize한다. Loss는 다음과 같이 된다.

\[\begin{equation} \mathbb{E}_{\bar{\alpha}, \epsilon} [\| \epsilon_\theta (\sqrt{\vphantom{1} \bar{\alpha}} y_0 + \sqrt{1 - \bar{\alpha}} \epsilon, x, \sqrt{\vphantom{1} \bar{\alpha}}) - \epsilon\|_1] \end{equation}\]

Score matching 프레임워크에서도 유사한 접근 방식이 사용되었으며, noise 분산으로 컨디셔닝했다.

이 접근 방식에서 해결해야 하는 사소한 기술적 문제가 하나 있다. 불연속 iteration 인덱스를 조건으로 하는 diffusion probabilistic model 학습 절차에서 \(n \sim \textrm{Uniform}(\{1, \cdots, N\})\)을 샘플링한 다음 해당 $\alpha_n$을 계산한다. 연속적인 noise level을 직접 컨디셔닝할 때 $\alpha$를 직접 샘플링할 수 있는 샘플링 절차를 정의해야 한다.

Uniform distribution $\bar{\alpha}_n \sim \textrm{Uniform}(0, 1)$에서 간단히 샘플링할 수 있지만, 이것이 좋지 않은 경험적 결과를 제공. 대신 개별 샘플링 전략을 모방하는 간단한 계층적 샘플링 방법을 사용한다. 먼저 $S$번의 iteration으로 noise schedule을 정의하고 해당 $\sqrt{\vphantom{1} \bar{\alpha}_s}$를 모두 계산한다.

\[\begin{equation} l_0 = 1, \quad l_s = \sqrt{\prod_{i=1}^s (1-\beta_i)} \end{equation}\]

먼저 segment $(l_{s-1}, l_s)$를 위한 \(s \sim U(\{1, \cdots, S\})\)를 샘플링한 다음, 이 segment에서 균일하게 샘플링하여 $\sqrt{\vphantom{1} \bar{\alpha}}$를 계산한다. 이 샘플링 절차를 사용한 WaveGrad 학습 알고리즘은 Algorithm 1과 같다.

이 방법의 이점 중 하나는 모델을 한 번만 학습하면 재학습 필요 없이 넓은 궤적 space에서 inference를 실행할 수 있다는 것이다. 구체적으로, 일단 모델을 학습시키면 inference 중에 다른 수의 iteration $N$을 사용할 수 있으므로 하나의 모델에서 inference 계산과 출력 품질 사이를 명시적으로 절충할 수 있다.

전체 inference 알고리즘은 Algorithm 2에 설명되어 있다.

전체 WaveGrad 아키텍처는 아래 그림에 시각화되어 있다.

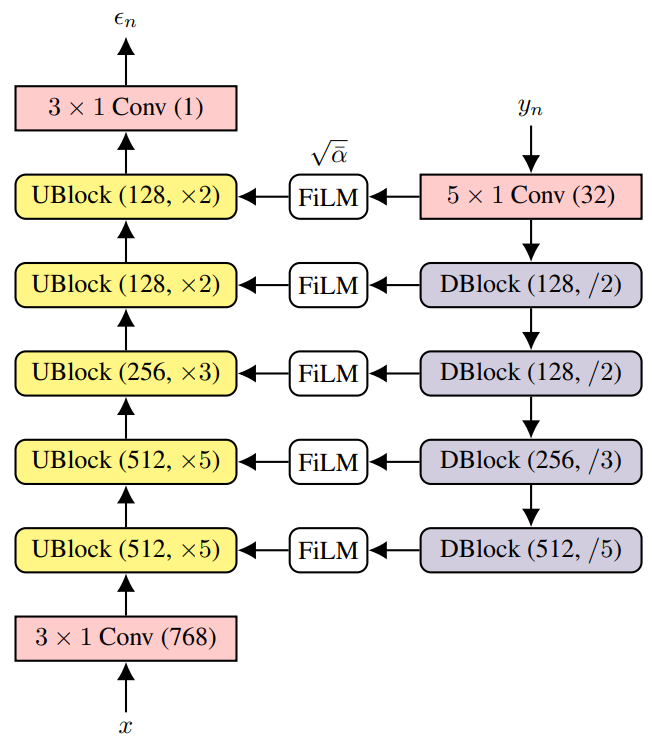
Experiments

• 데이터셋: 자체 음성 데이터셋 사용 (385시간, 영어, 84명), 24kHz로 downsampling 후 128차원의 mel-spectrogram feature (50ms Hanning window, 12.5ms frame shift, 2048-point FFT, 20 Hz & 12 kHz lower & upper frequency cutoffs) 추출
• 컨디셔닝 feature $x$: 학습 시에는 ground-truth 오디오에서 계산한 mel-spectrogram을 사용, Inference 시에는 Tacotron 2 모델이 예측한 mel-spectrogram을 사용
• Vocoder: 사전 학습된 text-to-spectrogram model에 의존하지 않고 대규모 corpus에서 개별적으로 학습될 수 있음
• Model size
  • Base: 입력은 24 프레임 (0.3초), 샘플 7,200개, batch size 256, 15M parameter, 1M step 학습
  • Large: UBlock과 DBlock을 각각 2개 사용 (하나만 up/downsampling), 입력은 60 프레임 (0.75초), 샘플 18,000개, batch size 256, 23M parameter, 1M step 학습

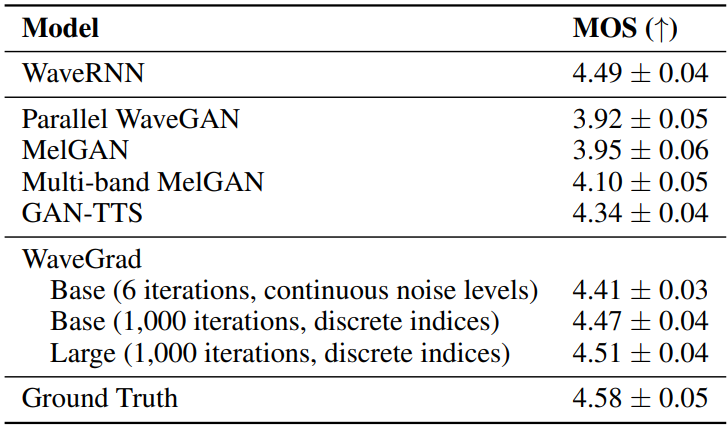
다음은 WaveGrad를 다양한 모델들과 MOS(Mean opinion scores)로 비교한 표이다. WaveRNN을 제외한 모든 모델은 non-autoregressive이다. WaveGrad, Parallel WaveGAN, MelGAN, Multiband MelGAN은 ground truth 오디오에서 계산된 mel-spectrogram을 컨디셔닝되었다. WaveRNN과 GAN-TTS는 예측된 feature를 학습에 사용하였다.

다음은 WaveGrad Base model에 대한 객관적 및 주관적 평가 결과이다.

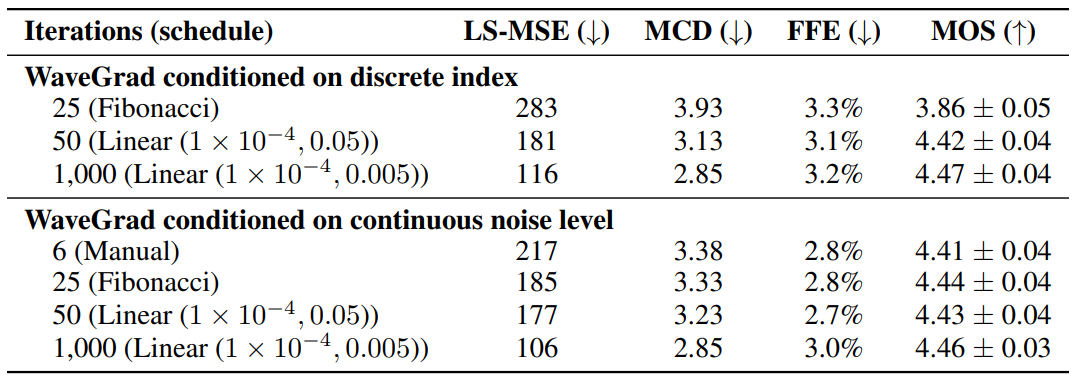
사용한 metric은 다음과 같다.

1. Log-mel spectrogram mean squared error metrics (LS-MSE)
2. Mel cepstral distance (MCD)
3. $F_0$ Frame Error (FFE)