[논문리뷰] Wavelet Latent Diffusion (WaLa): Billion-Parameter 3D Generative Model with Compact Wavelet Encodings

arXiv 2024. [Paper] [Page] [Github]
Aditya Sanghi, Aliasghar Khani, Pradyumna Reddy, Arianna Rampini, Derek Cheung, Kamal Rahimi Malekshan, Kanika Madan, Hooman Shayani
Autodesk AI Lab | Autodesk Research
12 Nov 2024

Introduction

대규모 3D 데이터에서 생성 모델을 학습하는 것은 상당한 과제를 안겨준다.

3D 데이터는 모델이 처리해야 하는 입력 변수의 수를 크게 증가시켜 이미지나 자연어 task의 복잡성을 훨씬 초과한다. 이러한 복잡성은 저장 및 스트리밍 문제로 인해 더욱 복잡해진다. 이처럼 대규모 모델을 학습하려면 종종 클라우드 서비스가 필요하므로 고해상도 3D 데이터셋의 경우 프로세스가 비싸다. 이러한 데이터셋은 상당한 공간을 차지하고 학습 중에 스트리밍 속도가 느리기 때문이다.
다른 데이터 유형과 달리 3D 모양은 voxel, 포인트 클라우드, 메쉬, implicit function과 같이 다양한 방식으로 표현할 수 있다. 각 표현은 품질과 압축성 간에 서로 다른 trade-off를 이룬다. 효율적인 학습 및 생성을 위해 고충실도와 압축성을 가장 잘 균형 잡는 표현을 결정하는 것은 여전히 미해결 과제이다.
3D 표현은 종종 여러 스케일의 디테일이 있는 복잡한 계층적 구조를 나타내므로 생성 모델이 글로벌 구조와 세분화된 디테일을 동시에 캡처하는 것이 어렵다.

한 가지 두드러진 컴팩트한 입력 표현은 웨이블릿 기반 표현으로, 웨이블릿 변환과 그 역변환을 활용하여 웨이블릿 공간과 고해상도 TSDF 표현 사이를 원활하게 변환한다. 이러한 방법은 몇 가지 주요 이점을 제공한다. 선택한 계수를 최소한의 디테일 손실로 삭제하여 데이터를 쉽게 압축할 수 있으며 계수 간의 상호 관계를 통해 TSDF를 직접 사용하는 경우에 비해 대규모 3D 데이터셋의 효율적인 저장, 스트리밍, 처리가 용이하다. 그러나 이러한 이점에도 불구하고 웨이블릿 기반 표현은 여전히 상당히 크며, 특히 대규모 생성 모델로 확장할 때 그렇다. 예를 들어, $256^3$ TSDF는 $46^3 \times 64$ 크기의 wavelet-tree로 표현할 수 있으며, 이는 1440$\times$1440 RGB 이미지와 동일하다. 이 공간 내에서의 스케일링은 계속해서 상당한 과제를 안겨준다.

본 논문은 웨이블릿 표현을 기반으로 하는 Wavelet Latent Diffusion (WaLa) 프레임워크를 소개한다. 이 프레임워크는 웨이블릿 표현을 추가로 압축하여 정보 손실 없이 압축된 latent 인코딩을 얻어, 이 공간에서 diffusion 기반 생성 모델을 효율적으로 스케일링할 수 있게 한다.

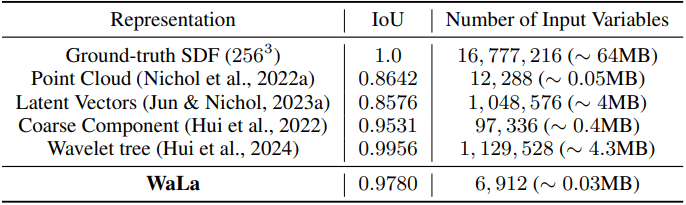
먼저, Make-A-Shape에서 설명한 것처럼 TSDF를 3D wavelet-tree 표현으로 변환한다. 그런 다음, adaptive sampling loss와 balanced fine-tuning을 통해, $256^3$ TSDF를 $12^3 \times 4$ 그리드로 압축하는 convolution 기반 VQ-VAE 모델을 학습시켜, 2,427배의 놀라운 압축 비율을 달성하면서도 디테일의 손실 없이 인상적인 재구성을 유지한다. 예를 들어, GSO 데이터셋에서 0.978의 IOU를 달성했다.

다른 표현과 비교했을 때, 이 접근 방식은 높은 재구성 정확도를 유지하면서 생성 모델의 입력 변수 수를 줄인다. 결과적으로 생성 모델은 로컬 디테일을 모델링할 필요 없이 전반적인 구조를 캡처하는 데 집중할 수 있다. 또한, 이 압축으로 인해 생성 모델이 처리해야 하는 입력 변수의 수가 크게 줄어들어, 최대 10억 개의 파라미터를 가진 대규모 3D 생성 모델의 학습이 가능해져 매우 세밀하고 다양한 형상을 생성할 수 있다.

WaLa는 여러 입력 모달리티를 통한 조건부 생성을 지원한다. 그 결과, 복잡한 기하학적 구조, 타당한 구조, 복잡한 위상, 매끄러운 표면을 가진 3D shape을 생성할 수 있다. 이는 텍스트, 스케치, 저해상도 voxel, 포인트 클라우드, 단일 뷰 이미지, 멀티뷰 이미지와 같은 다양한 입력 모달리티로부터 생성된 SDF에 Marching Cubes를 적용하여 고품질 3D 메쉬를 얻을 수 있다.

Method

대규모 3D 데이터에서 생성 모델을 학습하는 것은 데이터의 복잡성과 크기 때문에 어렵다. 이로 인해 웨이블릿과 같은 컴팩트한 표현이 생성되어 효율적인 신경망 학습이 용이해졌다. 웨이블릿으로 3D shape을 표현하려면 먼저 TSDF 그리드로 변환한다. 그런 다음 웨이블릿 변환을 적용하여 이 TSDF 그리드를 coarse 계수 $C_0$와 다양한 레벨의 detail 계수 $D_0$, $D_1$, $D_2$로 분해한다. 다양한 웨이블릿 변환을 사용할 수 있지만, 대부분의 현재 방법은 biorthogonal 웨이블릿 변환을 사용한다. Coarse 계수는 주로 필수적인 shape 정보를 캡처하는 반면 detail 계수는 고주파 디테일을 나타낸다. 이 표현을 압축하려면 다양한 필터링 방식을 적용하여 특정 계수를 제거할 수 있지만 재구성 품질이 떨어지게 된다.

Wavelet-tree 표현은 모든 coarse 계수 $C_0$를 유지하고, 세 번째 레벨의 detail 계수 $D_2$를 삭제하고, subband 계수 필터링 방식을 사용하여 $D_0$의 가장 중요한 계수와 $D_1$의 해당 디테일을 선택적으로 유지한다.

본 논문의 방법에는 많은 3D shape 컬렉션이 필요하다. $\mathcal{S} = \{(W_n, \Theta_n)\}_{n=1}^N$을 $N$개의 3D shape으로 구성된 데이터셋이라 하면, 각 shape $S_n \in \mathcal{S}$는 diffusion 가능한 wavelet-tree 표현 $W_n$과 선택 사항인 조건 $\Theta_n$으로 표현된다. $W_n \in \mathbb{R}^{46^3 \times 64}$은 해상도 $256^3$의 TSDF를 변환하여 얻는다. 조건부 생성 모델에 따라 조건 $\Theta_n$은 단일 뷰 이미지, 멀티뷰 이미지, voxel 표현, 포인트 클라우드, 멀티뷰 depth map이 될 수 있으며 모델이 unconditional하거나 VQ-VAE를 학습할 때 생략될 수 있다.

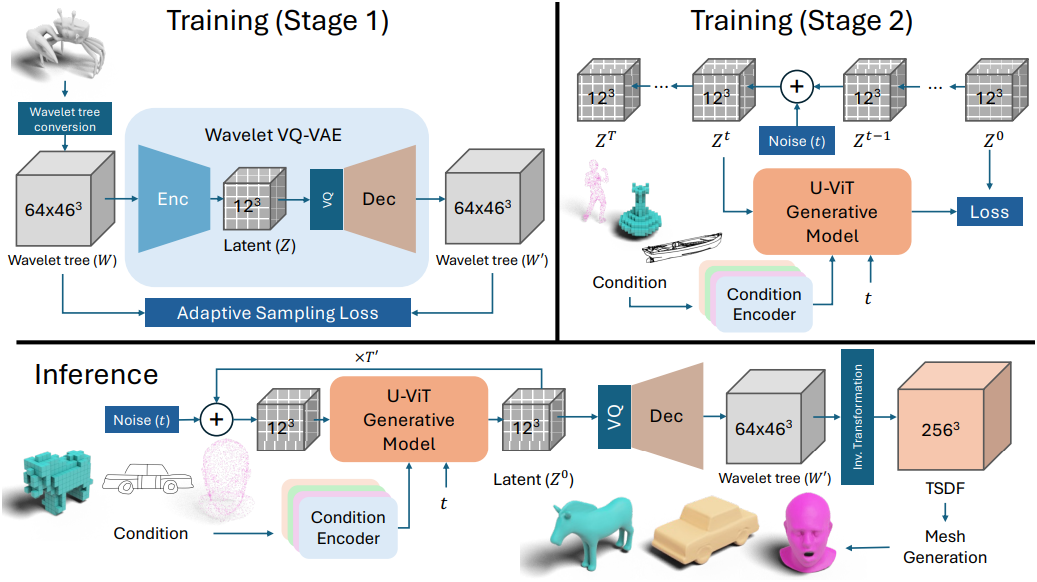
모델의 학습은 두 단계로 구성된다. 먼저, adaptive sampling loss를 사용하여 wavelet-tree 표현을 보다 컴팩트한 그리드 latent space $Z$로 인코딩하기 위해 convolution 기반 VQ-VAE를 학습시킨다. 이 단계에서는 재구성 정확도를 더욱 높이기 위해 balanced fine-tuning이라고 하는 간단한 접근 방식을 사용하여 VQ-VAE를 fine-tuning한다. 이 VQ-VAE는 각 shape $S_n$에 대해 latent grid $Z_n \in \mathbb{R}^{12^3 \times 4}$를 인코딩한다.

두 번째 단계에서는 이 latent grid $Z_n$에서 diffusion model을 학습시키며, 이 diffusion model은 앞서 언급한 조건 중 하나에서 파생된 조건 벡터 시퀀스로 컨디셔닝할 수 있다. Inference하는 동안 classifier-free guidance를 활용하여 reverse process를 통해 완전히 noise가 있는 latent 벡터로 시작에서 점진적으로 noise를 제거한다.

1. Stage 1: Wavelet VQ-VAE

주요 목표는 충실도를 크게 잃지 않고 wavelet-tree 표현을 컴팩트한 latent space로 압축하여 이 latent space에서 직접 생성 모델을 학습하는 것을 용이하게 하는 것이다. 압축을 생성에서 분리하면 latent space 내에서 큰 생성 모델을 효율적으로 확장할 수 있다.

이를 위해 더 선명한 재구성을 생성하고 posterior collapse와 같은 문제를 완화하는 것으로 알려진 convolution 기반 VQ-VAE를 사용한다. 구체적으로, 인코더 $\textrm{Enc}(\cdot)$는 입력 $W_n$을 latent 표현 $Z_n = \textrm{Enc}(W_n)$에 매핑한 vector quantization layer를 통해 $\textrm{VQ}(Z_n)$으로 quantize하고 $\textrm{Dec}(\cdot)$로 디코딩하여 shape $W_n^\prime = \textrm{Dec}(\textrm{VQ}(Z_n))$을 재구성한다. Vector quantization layer를 디코더와 통합함으로써 생성 모델이 사전에 quantize된 latent code에서 학습되도록 한다. 이 접근 방식은 생성된 latent code를 codebook의 가장 가까운 임베딩에 매핑하여 quantization layer의 robustness를 활용한다.

VQ-VAE를 학습시키기 위해 세 가지 loss의 조합을 사용한다.

Reconstruction loss: 원래 shape과 재구성된 shape 간의 충실도를 보장
Codebook loss: codebook 임베딩이 인코더 출력 분포에 적응하도록 장려
Commitment loss: 인코더의 출력을 codebook 임베딩과 밀접하게 정렬

Reconstruction loss $\mathcal{L}_\textrm{rec} (W_n, W_n^\prime)$을 적용하는 동안 Make-A-Shape의 adaptive sampling loss 전략을 채택하여 다른 계수를 고려하면서도 $D_0$와 $D_1$에 더 효과적으로 집중한다.

이 접근 방식은 가장 큰 계수에 대한 상대적 크기를 기준으로 각 subband에서 계수들의 중요성을 식별하여 중요한 좌표의 집합 $P_0$를 형성한다. 이러한 중요한 계수를 강조하도록 학습 loss를 구조화하고 덜 중요한 계수의 무작위 샘플링을 통합함으로써 모델은 디테일을 소홀히 하지 않고 핵심 정보에 효율적으로 집중한다.

\[\begin{equation} \mathcal{L}_\textrm{rec} = L_\textrm{MSE} (C_0, C_0^\prime) + \frac{1}{2} \sum_{D \in \{D_0, D_1\}} [L_\textrm{MSE} (D [P_0], D^\prime [P_0]) + L_\textrm{MSE} (R (D [P_0^\prime]), R (D^\prime [P_0^\prime]))] \end{equation}\]

$D [P_0]$는 집합 $P_0$에서 지정한 위치에 있는 $D$의 계수이며, $P_0^\prime$은 $P_0$의 여집합이다. 함수 $R(D)$는 선택된 계수의 수가 $\vert P_0 \vert$와 같도록 $D$에서 계수를 무작위로 선택한다. Loss function의 마지막 두 항에서 계수의 수를 균형 있게 조정함으로써, 덜 중요한 계수를 정규화하면서 중요한 정보를 강조힌다.

모델은 처음에 19개의 서로 다른 데이터셋에서 수집한 1,000만 개의 샘플로 학습되었다. 그러나 이 데이터의 상당 부분이 간단한 CAD 객체에 치우쳐 있어 학습 과정에 편향이 발생하였다. 이러한 불균형으로 인해 모델이 더 복잡하거나 덜 표현된 3D shape에서 성능이 저하될 수 있다.

이 문제를 해결하기 위해 19개 데이터셋 각각에서 동일한 수의 샘플을 사용하여 수렴된 VQ-VAE 모델을 fine-tuning한다. 이 프로세스를 balanced fine-tuning이라고 한다. 이 접근 방식은 모델이 모든 데이터셋에 존재하는 다양한 shape과 복잡성에 균일하게 노출되도록 하여 초기 불균형으로 인해 발생하는 편향을 줄인다. 경험적으로 balanced fine-tuning은 데이터셋 전체에서 재구성 결과를 향상시킨다.

2. Stage 2: Latent Diffusion Model

두 번째 단계에서는 latent grid에서 수십억 개의 파라미터를 갖는 대규모 생성 모델을 학습시킨다. 모델은 데이터 분포를 포착하기 위한 unconditional 모델이거나 다양한 모달리티 $\Theta_n$ (ex. 포인트 클라우드, 폭셀, 이미지)으로 컨디셔닝된다. 저자들은 DDPM 프레임워크 내에서 생성 프로세스를 두 단계의 Markov chain으로 모델링하였다.

먼저, diffusion process는 $T$ step에 걸쳐 초기 latent code $Z_n^0$에 Gaussian noise를 점진적으로 추가하여 $Z_n^T \sim \mathcal{N} (0, I)$을 생성한다. 그런 다음, reverse process는 $\Theta_n$으로 컨디셔닝된 생성기 $θ$를 사용하여 noise를 제거하고 $Z_n^0$을 재구성한다. 생성기는 $f_\theta (Z_n^t, t, \Theta_n) \approx Z_n^0$을 사용하여 timestep $t$에서 모든 중간 latent code $Z_n^t$에서 원래 latent code $Z_n^0$을 예측하고 MSE loss를 사용하여 최적화한다.

\[\begin{equation} \mathcal{L} = \mathbb{E}_t [\| f_\theta (Z_n^t, t, \Theta_n) - Z_n^0 \|^2] \end{equation}\]

여기서 $Z_n^t$는 cosine noise schedule을 사용하여 timestep $t$에서 Gaussian noise $\epsilon$을 $Z_n^0$에 추가하여 얻는다. 조건 $\Theta_n$은 다양한 컨디셔닝 모달리티에서 파생된 벡터의 latent 집합으로, cross-attention을 사용하고 ResNet과 cross-attention layer에서 정규화 파라미터를 변조하여 U-ViT 생성기에 주입한다. 이는 다양한 모달리티에 대한 조건 인코더를 통해 달성된다.

학습하는 동안 classifier-free guidance를 구현하기 위해 조건에 작은 dropout을 적용한다. 대부분 입력 조건의 경우 각 조건에 대해 다른 조건 생성 모델을 직접 학습하는 반면, 스케치와 단일 깊이에 대한 컨디셔닝의 경우 이미지 조건부 생성 모델을 가져와 각각 합성 스케치 데이터와 깊이 데이터로 fine-tuning한다. Text-to-3D의 경우, MVDream을 fine-tuning하여 6개의 멀티뷰 depth 이미지를 생성하는데, 이는 멀티뷰 이미지보다 더 나은 재구성을 제공한다.

3. Inference

Inference 시에는 $Z_n^T \sim \mathcal{N} (0, I)$으로 시작하여 reverse process를 통해 원래의 latent code $Z_n^0$을 재구성하기 위해 반복적으로 noise를 제거한다. 조건부 생성의 경우 classifier-free guidance를 적용하여 생성 프로세스를 원하는 출력으로 조정한다. 이 접근 방식을 사용하면 품질-다양성 trade-off를 더 잘 제어할 수 있다.

최종 latent code $Z_n^0$을 얻으면 VQ-VAE의 사전 학습된 디코더 네트워크를 사용하여 wavelet 형태의 최종 3D shape을 생성한다. 그런 다음 역 웨이블릿 변환을 적용하여 최종 3D shape을 TSDF로 얻고 marching cubes를 사용하여 메쉬로 추가로 변환할 수 있다. 특히 다양한 랜덤 noise를 사용하여 동일한 조건부 입력에 대해 여러 샘플을 생성할 수 있다.

Experiments

데이터셋: ModelNet, ShapeNet, SMPL, Thingi10K, SMAL, COMA, House3D, ABC, Fusion 360, 3D-FUTURE, BuildingNet, DeformingThings4D, FG3D, Toys4K, ABO, Infinigen, Objaverse, ObjaverseXL (Thingiverse and GitHub)
학습 디테일
- optimizer: Adam
- learning rate: 0.0001
- gradient clipping: 1
- VQ-VAE
  - batch size: 256
  - codebook: 임베딩 1024개, 차원 = 4
  - 학습이 수렴한 후 balanced fine-tuning
- 생성 모델
  - batch size: 64
  - iteration: 입력 조건에 따라 200만 ~ 400만
  - 각 조건마다 H100 GPU 1개로 학습
- WaLa Large
  - batch size: 256
  - H100 GPU 8개