[논문리뷰] VQ-Diffusion: Vector Quantized Diffusion Model for Text-to-Image Synthesis

CVPR 2022 (Oral). [Paper] [Github]
Shuyang Gu, Dong Chen, Jianmin Bao, Fang Wen, Bo Zhang, Dongdong Chen, Lu Yuan, Baining Guo
Microsoft Research
29 Nov 2021

Introduction

DALL-E와 같은 기존 autoregressive(AR) 모델들의 텍스트에서 이미지로의 생성 방법에는 여전히 개선해야 할 문제가 있다. 한 가지 문제는 단방향 편향(unidirectional bias)이다. 기존 방법은 모든 prefix 픽셀/토큰과 텍스트 설명에 대한 attention을 기반으로 왼쪽 위에서 오른쪽 아래로 픽셀 또는 토큰을 예측한다. 이 고정된 순서는 합성된 이미지에 부자연스러운 편향을 가져온다. 이는 중요한 컨텍스트 정보가 왼쪽이나 위뿐만 아니라 이미지의 모든 부분에서 나올 수 있기 때문이다.

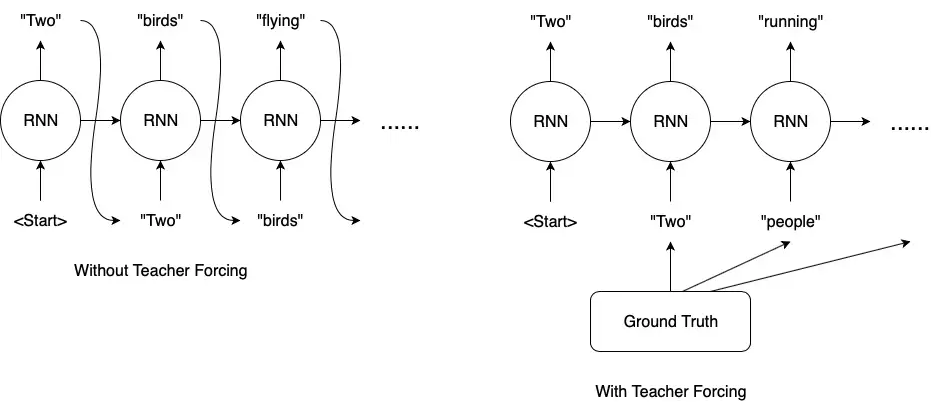
또 다른 문제는 누적된 예측 오차(accumulated prediction error)이다. Inference 단계의 각 step은 이전에 샘플링된 토큰을 기반으로 수행된다. 이와 다르게 학습 과정에서는 “teacher-forcing” 전략을 사용하여 각 step에 대한 ground truth를 제공한다. 이 차이는 중요하며 그 결과는 주의 깊게 검토할 가치가 있다. 특히, inference 단계의 토큰은 일단 예측되면 수정할 수 없으며 이 때 발생한 오차가 후속 토큰으로 전파된다.

저자들은 단방향 편향을 제거하고 누적된 예측 오차를 방지하는 text-to-image 생성을 위한 vector quantized diffusion (VQ-Diffusion) model을 제시한다. VQ-VAE(vector quantized variational autoencoder)로 먼저 코드북을 학습한 뒤 DDPM(Denoising Diffusion Probabilistic Model (논문리뷰))의 조건부 버전으로 모델을 학습하여 latent space를 모델링한다. 저자들은 latent space 모델이 text-to-image 생성 task에 적합하다는 것을 보여준다.

VQ-Diffusion 모델은 고정된 Markov chain을 통해 입력을 점진적으로 손상시키는 forward diffusion process를 reverse하여 데이터 분포를 샘플링한다. Forward process는 입력과 동일한 차원의 noise가 증가하는 latent variable 시퀀스를 생성하여 고정된 개수의 timestep 후에 순수한 noise를 생성한다. Reverse process는 조건부 분포를 학습하여 순수한 noise에서 시작하여 원하는 데이터 분포를 향해 점진적으로 잠재 변수를 denoise한다.

VQ-Diffusion 모델은 독립적인 text encoder와 diffusion image decoder로 discrete 이미지 토큰에서 denoising diffusion을 수행한다. Inference 단계가 시작될 때 모든 이미지 토큰은 마스킹되거나 랜덤이다. 여기서 마스킹된 토큰은 마스크 기반 생성 모델과 동일한 기능을 수행한다. Denoising diffusion process는 입력 텍스트를 기반으로 점진적으로 이미지 토큰의 확률 밀도를 추정한다. 각 step에서 diffusion image decoder는 이전 step에서 예측된 전체 이미지의 모든 토큰의 컨텍스트 정보를 활용하여 새로운 확률 밀도 분포를 추정하고 이 분포를 사용하여 현재 step의 토큰을 예측한다. 이 양방향 attention은 각 토큰 예측에 대한 전역 컨텍스트를 제공하고 단방향 편향을 제거한다.

또한 VQ-Diffusion 모델은 mask-and-replace diffusion 전략을 사용하여 오차 누적을 방지한다. VQ-Diffusion은 학습 단계에서 “teacher-forcing” 전략을 사용하지 않는다. 대신, 의도적으로 마스킹된 토큰과 무작위 토큰을 모두 도입하고 네트워크가 마스킹된 토큰을 예측하고 잘못된 토큰을 수정하는 방법을 배우도록 한다. Inference 단계에서는 각 step에서 모든 토큰의 밀도 분포를 업데이트하고 새로운 분포에 따라 모든 토큰을 리샘플링한다. 따라서 잘못된 토큰을 수정하고 오차 누적을 방지할 수 있다. Unconditional 이미지 생성을 위한 기존 replace-only diffusion 전략과 비교할 때 마스크된 토큰은 마스크된 영역으로 네트워크의 attention을 효과적으로 유도하여 네트워크에서 검사할 토큰 조합의 수를 크게 줄인다. 이 mask-and-replace diffusion 전략은 네트워크의 수렴을 크게 가속화한다.

저자들은 VQ-Diffusion 방법의 성능을 평가하기 위해 CUB-200, Oxford102 및 MSCOCO를 포함한 다양한 데이터셋으로 text-to-image 생성을 실험하였다. 비슷한 수의 파라미터를 가진 AR(autoregressive) 모델과 비교할 때, VQ-Diffusion 방법은 훨씬 더 나은 이미지 품질을 달성하고 훨씬 빠르다. 또한 기존의 GAN 기반 text-to-image 방법과 비교하여 더 복잡한 scene을 처리할 수 있으며 합성 이미지 품질이 크게 향상되었다. DALL-E 및 CogView를 포함한 초대형 모델(VQ-Diffusion 모델보다 매개변수가 10배 더 많은 모델)과 비교할 때, VQ-Diffusion 모델은 특정 유형의 이미지, 즉 학습 중에 모델이 본 이미지 유형에 대해 비슷하거나 더 나은 결과를 달성한다. 또한, FFHQ 및 ImageNet을 사용한 unconditional 및 conditional 이미지 생성에 대한 실험에서 강력한 결과를 생성한다.

또한 VQ-Diffusion 모델은 inference 속도에 중요한 이점이 있다. 기존의 AR 방법에서는 출력 이미지 해상도에 따라 inference 시간이 선형적으로 증가하고 일반 크기 이미지의 경우에도 이미지 생성에 상당한 시간이 소요된다. 반면 VQ-Diffusion은 각 토큰 예측에 대한 글로벌 컨텍스트를 제공하여 inference 시간을 이미지 해상도와 독립적으로 만든다. 이를 통해 diffusion image decoder의 간단한 reparameterization를 통해 inference 속도와 이미지 품질 간의 더 나은 tradeoff를 달성할 수 있다. 특히, 각 step에서 디코더에게 다음 denoising diffusion step에서 noise가 감소된 이미지 대신 noise가 없는 원래 이미지를 예측하도록 요청한다. 실험을 통해 reparameterization를 사용한 VQ-Diffusion 방법이 AR 방법보다 15배 더 빠르면서도 더 나은 이미지 품질을 달성할 수 있음을 발견했다.

Background: Learning Discrete Latent Space of Images Via VQ-VAE

VQ-VAE는 인코더 $E$와 디코더 $D$, 그리고 임베딩 벡터들을 포함하는 코드북 \(\mathcal{Z} = \{z_k\}_{k=1}^K \in \mathbb{R}^{K \times d}\)으로 이루어져 있다. $K$는 코드북의 크기(임베딩 벡터의 개수)이며 $d$는 코드의 차원이다. 주어진 이미지 $x$에 대하여, $z = E(x) \in \mathbb{R}^{h \times w \times d}$를 spatial-wise quantizer $Q(\cdot)$에 넣어 각 spatial feature $z_{ij}$를 가장 가까운 코드 $z_k$에 매핑한 이미지 토큰 $z_q$를 얻는다.

\[\begin{equation} z_q = Q (z) = \bigg( \underset{z_k \in \mathcal{Z} }{\arg \min} \| z_{ij} - z_k \|_2^2 \in \mathbb{R}^{h \times w \times d} \bigg) \end{equation}\]

여기서 $h \times w$는 인코딩된 시퀀스의 길이이며 $H \times W$보다 작다. 그런 다음 디코더를 통해 $\tilde{x} = G(z_q)$로 이미지를 재구성한다. 따라서 이미지 합성은 latent 분포에서 이미지 토큰을 샘플링하는 것과 같다. 이미지 토큰은 불연속 값을 취한다는 점에서 양자화된 latent 변수이다. 인코더 $E$, 디코더 $G$ 및 코드북 $Z$는 다음 손실 함수를 통해 end-to-end로 학습된다.

\[\begin{equation} \mathcal{L}_{\textrm{VQVAE}} = \|x - \tilde{x} \|_1 + \| \textrm{sg}[E(x)] - z_q \|_2^2 + \beta \| \textrm{sg}[z_q] - E(x) \|_2^2 \end{equation}\]

sg는 stop-gradient 연산이다. 실제로는 위 손실 함수를 사용하는 것보다 코드북 업데이트를 위한 두번째 항을 exponential moving averages (EMA)로 바꾸는 것이 더 좋다고 입증되었다.

Vector Quantized Diffusion Model

주어진 텍스트-이미지 쌍에 대하여 이산 이미지 토큰 $x \in \mathbb{Z}^N$을 pretrained VQ-VAE로부터 얻는다. 여기서 $N = hw$는 토큰 시퀀스의 길이이다. VQ-VAE 코드북을 $K$라 가정하면, 위치 $i$의 이미지 토큰 \(x_i \in \{1, 2, \cdots, K\}\)는 코드북의 index 중 하나이다. 반면, 텍스트 토큰 $y \in \mathbb{Z}^M$은 BPE-encoding으로 얻을 수 있다. 전체 text-to-image 프레임워크는 조건부 분포 $q(x \vert y)$를 최대화한다고 볼 수 있다.

DALL-E나 CogView와 같은 AR 모델은 이전에 예측된 이미지 토큰뿐만 아니라 텍스트 토큰에 따라 각 이미지 토큰을 순차적으로 예측한다.

\[\begin{equation} q(x|y) = \prod_{i=1}^N q(x^i | x^1, \cdots, x^{i-1}, y) \end{equation}\]

AR 모델링은 text-to-image 합성에서 놀라운 품질을 달성하지만 몇 가지 제한 사항이 있다.

1. 이미지 토큰은 raster scan과 같은 단방향 순서로 예측되는데, 이는 특정 위치의 예측이 단순히 왼쪽이나 위의 컨텍스트에만 주의를 기울여서는 안 되기 때문에 2D 데이터의 구조를 무시하고 이미지 모델링에 대한 표현력을 제한한다.
2. 학습은 ground truth을 사용하는 반면 inference는 이전 토큰과 같은 예측에 의존하기 때문에 학습과 inference 사이의 불일치가 있다. “Teacher-forcing” 또는 exposure bias는 이전 샘플링의 실수로 인해 오차 누적으로 이어진다. 또한, 각 토큰을 예측하기 위해서는 네트워크의 forward pass가 필요하며, 이는 저해상도의 latent space (32$\times$32)에서 샘플링하는 데에도 과도한 시간을 소비하므로 실제 사용에는 AR 모델이 비실용적이다.

VQ-Diffusion는 AR이 아닌 방식으로 VQ-VAE latent space를 모델링하는 것을 목표로 한다. VQ-Diffusion 방법은 확산 모델로 확률 $q(x \vert y)$를 최대화하며, 이미지 합성에서 뛰어난 품질을 생성하는 새로운 접근 방식이다. 최근 연구들의 대부분은 연속적인 diffusion model에 초점을 맞추고 있지만 카테고리 분포를 사용하는 연구는 훨씬 적다. 이 논문에서는 text-to-image 생성을 위해 조건부 버전의 discrete diffusion process를 사용할 것을 제안한다. 이어서 MLM(Masked Language Modeling)에서 영감을 받은 discrete diffusion process를 소개하고 이 process를 reverse 시키기 위해 신경망을 학습시키는 방법에 대해 논의한다.

1. Discrete diffusion process

Forward diffusion process는 고정된 Markov chain \(q(x_t \vert x_{t-1})\)을 통해 이미지 데이터 $x_0$을 점진적으로 손상시킨다. 예를 들어 \(x_{t-1}\)의 일부 토큰을 임의로 교체한다. 고정된 수의 $T$ timestep 이후, forward process는 $z_0$과 동일한 차원의 noise가 증가하는 잠재 변수 $z_1, \cdots, z_T$의 시퀀스를 생성하고 $z_T$는 순수한 noise 토큰이 된다. Reverse process는 noise $z_T$에서 시작하여 latent variable의 noise를 점진적으로 제거하고 reverse distribution \(q(x_{t-1} \vert x_t, x_0)\)에서 순차적으로 샘플링하여 실제 데이터 $x_0$을 복원한다. 그러나 inference 단계에서 $x_0$을 알 수 없기 때문에 전체 데이터 분포에 따라 달라지는 조건부 분포 \(p_\theta (x_{t−1} \vert x_t, y)\)를 근사화하도록 transformer를 학습한다.

코드북의 index, 즉 \(x_0^i \in \{1, 2, \cdots, K\}\)를 사용하는 위치 i에서의 $x_0$의 단일 이미지 토큰 $x_0^i$을 고려하자. 간단한 설명을 위해 위첨자 i를 생략한다. 행렬 \([Q_t]_{mn} = q(x_t = m \vert x_{t−1} = n) \in \mathbb{R}^{K \times K}\)를 사용하여 $x_{t−1}$이 $x_t$로 이동할 확률을 정의한다. 그런 다음 전체 토큰 시퀀스에 대한 forward Markov diffusion process를 다음과 같이 쓸 수 있다.

\[\begin{equation} q(x_t | x_{t-1}) = v^\top (x_t) Q_t v(x_{t-1}) \end{equation}\]

여기서 $v(x)$는 길이가 $K$이고 $x$에 대한 index만 1인 one-hot 열 벡터이다. $x_t$에 대한 카테고리 분포는 벡터 $Q_t v(x_{t−1})$로 주어진다. 중요한 것은 Markov chian의 속성으로 인해 다음과 같이 중간 step을 무시하고 $x_0$에서 직접 임의의 timestep에서의 $x_t$의 확률을 도출할 수 있다는 것이다.

\[\begin{equation} q_t(x_t | x_0) = v^\top (x_t) \overline{Q}_t v(x_0), \quad \overline{Q}_t = Q_t \cdots Q_1 \end{equation}\]

또 다른 주목할 만한 특징은 $z_0$에 conditioning함으로써 다음과 같이 이 diffusion process의 사후 확률(posterior)이 tractable하다는 것이다.

\[\begin{equation} q(x_{t-1} | x_t, x_0) = \frac{q(x_t | x_{t-1}, x_0) q(x_{t-1} | x_0)}{q(x_t | x_0)} = \frac{(v^\top (x_t) Q_t v(x_{t-1})) (v^\top (x_{t-1}) \overline{Q}_{t-1} v(x_0))}{v^\top (x_t) \overline{Q}_t v(x_0)} \end{equation}\]

Transition matrix $Q_t$는 discrete diffusion model에 매우 중요하며 reverse network가 noise에서 신호를 복구하는 것이 너무 어렵지 않도록 신중하게 설계되어야 한다. 이전 연구들에서는 카테고리 분포에 소량의 균일한 noise를 도입할 것이 제안되었으며 transition matrix은 다음과 같이 공식화될 수 있다.

\[\begin{equation} Q_t = \begin{bmatrix} \alpha_t + \beta_t & \beta_t & \cdots & \beta_t \\ \beta_t & \alpha_t + \beta_t & \cdots & \beta_t \\ \vdots & \vdots & \ddots & \vdots \\ \beta_t & \beta_t & \cdots & \alpha_t + \beta_t \end{bmatrix} \end{equation}\]

$\alpha_t \in [0,1]$이고 $\beta_t = (1-\alpha_t) / K$이다. 각 토큰은 $(\alpha_t + \beta_t)$의 확률로 그대로 있고 $K\beta_t$의 확률로 uniform하게 $K$ 카테고리 중 하나로 다시 샘플링된다.

그럼에도 불구하고 uniform diffusion을 사용하여 데이터를 손상시키는 것은 reverse estimation에 문제가 될 수 있는 다소 공격적인 process이다.

1. 순서형 데이터에 대한 Gaussian diffusion process와 달리 이미지 토큰은 완전히 상관관계가 없는 카테고리로 대체될 수 있으며, 이는 해당 토큰에 대한 갑작스러운 semantic 변경으로 이어진다.
2. 네트워크는 토큰을 수정하기 전에 교체된 토큰을 파악하기 위한 추가 노력을 기울여야 한다. 실제로 로컬 컨텍스트 내의 semantic 충돌로 인해 서로 다른 이미지 토큰에 대한 reverse estimation은 경쟁을 형성하고 신뢰할 수 있는 토큰을 식별하는 딜레마에 빠질 수 있다.

Mask-and-replace diffusion strategy

저자들은 위와 같은 uniform diffusion의 문제를 해결하기 위해 mask language modeling으로부터 영감을 얻어 손상된 위치가 reverse network에 의해 명시적으로 알려질 수 있도록 토큰 중 일부를 확률적으로 마스킹하여 토큰을 손상시킬 것을 제안한다. 특히 추가 특수 토큰인 [MASK] 토큰을 도입하여 이제 각 토큰이 $(K+1)$개의 discrete 상태를 가진다. 저자들은 mask diffusion을 다음과 같이 정의한다. 각 일반 토큰은 [MASK] 토큰으로 대체될 $\gamma_t$의 확률을 가지고 $K \beta_t$의 확률로 균일하게 diffusion이 일어나며 $\alpha_t = 1 - K \beta_t - \gamma_t$의 확률로 변경되지 않는다. 반면, [MASK] 토큰은 항상 자체 상태를 유지한다. 따라서 transition matrix $Q_t \in \mathbb{R}^{(K+1) \times (K+1)}$를 다음과 같이 공식화할 수 있다.

\[\begin{equation} Q_t = \begin{bmatrix} \alpha_t + \beta_t & \beta_t & \beta_t & \cdots & 0 \\ \beta_t & \alpha_t + \beta_t & \beta_t & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \gamma_t & \gamma_t & \gamma_t & \cdots & 1 \end{bmatrix} \end{equation}\]

이 mask-and-replace transition의 장점은 다음과 같다.

1. 손상된 토큰을 네트워크에서 식별할 수 있으므로 reverse process가 쉬워진다.
2. Mask-only 접근 방식과 비교했을 때 토큰 마스킹 외에 소량의 균일한 noise를 포함하는 것이 필요하다는 것을 이론적으로 증명한다. 그렇지 않으면 $x_t \ne x_0$일 때 작은 사후 확률을 얻는다.
3. 무작위 토큰 대체는 네트워크가 [MASK] 토큰에만 집중하기보다 컨텍스트를 이해하도록 강제한다.
4. 누적 transition matrix $\overline{Q}_t$와 확률 $q(x_t \vert x_0)$는 다음을 사용하여 닫힌 형식으로 계산할 수 있다.

\[\begin{equation} \overline{Q}_t v(x_0) = \overline{\alpha}_t v(x_0) + (\overline{\gamma}_t - \overline{\beta}_t) v(K+1) + \overline{\beta}_t \\ (\overline{\alpha}_t = \prod_{i=1}^t \alpha_i, \overline{\gamma}_t = 1- \prod_{i=1}^t (1 - \gamma_i), \overline{\beta}_t = \frac{1 - \overline{\alpha}_t - \overline{\gamma}_t}{K}) \end{equation}\]

증명)

---

수학적 귀납법으로 증명.
$t = 1$일 때, $$ \begin{equation} \overline{Q_1} v(x_0) = \begin{cases} \overline{\alpha}_1 + \overline{\beta}_1, & x = x_0 \\ \overline{\beta_1}, & x \ne x_0 \; \textrm{and} \; x \ne K + 1 \\ \overline{\gamma_1}, & x = K + 1 \end{cases} \end{equation} $$ 이므로 식이 성립한다. $t$에서 식이 성립할 때 $t+1$에서 식이 성립한다고 가정하자.
$t+1$에서 $$ \begin{equation} \overline{Q}_{t+1} v(x_0) = Q_{t+1} \overline{Q}_t v(x_0) \end{equation} $$ 이다. $x = x_0$일 때, $$ \begin{aligned} Q_{t+1} v(x_0)_{(x)} &= \overline{\beta}_t \beta_{t+1} (K-1) + (\alpha_{t+1} + \beta_{t+1}) (\overline{\alpha}_t + \overline{\beta}_t) \\ &= \overline{\beta}_t (K \beta_{t+1} + \alpha_{t+1}) + \overline{\alpha}_t (\alpha_{t+1} + \beta_{t+1}) \\ &= \overline{\beta}_t (1- \gamma_{t+1}) + \overline{\alpha}_{t+1} + \overline{\alpha}_t \beta_{t+1} \\ &= \frac{1}{K} (K \overline{\beta}_t (1-\gamma_{t+1}) + K \overline{\alpha}_t \beta_{t+1} - K \overline{\beta}_{t+1}) + \overline{\alpha}_{t+1} + \overline{\beta}_{t+1} \\ &= \frac{1}{K} [ (1 - \overline{\alpha}_t - \overline{\gamma}_t) (1-\gamma_{t+1}) + K \overline{\alpha}_t \beta_{t+1} - (1 - \overline{\alpha}_{t+1} - \overline{\gamma}_{t+1})] + \overline{\alpha}_{t+1} + \overline{\beta}_{t+1} \\ &= \frac{1}{K} [ (1-\overline{\gamma}_{t+1}) - \overline{\alpha}_t (1-\gamma_{t+1}) + K \overline{\alpha}_t \beta_{t+1} - (1 - \overline{\gamma}_{t+1}) + \overline{\alpha}_{t+1}] + \overline{\alpha}_{t+1} + \overline{\beta}_{t+1} \\ &= \frac{1}{K} [ (1-\overline{\gamma}_{t+1}) - \overline{\alpha}_t (1-\gamma_{t+1} - K \beta_{t+1}) - (1 - \overline{\gamma}_{t+1}) + \overline{\alpha}_{t+1}] + \overline{\alpha}_{t+1} + \overline{\beta}_{t+1} \\ &= \overline{\alpha}_{t+1} + \overline{\beta}_{t+1} \end{aligned} $$ $x = K + 1$일 때, $$ \begin{aligned} Q_{t+1} v(x_0)_{(x)} &= \overline{\gamma}_t + (1-\overline{\gamma}_t) \gamma_{t+1} \\ &= 1 - (1 - \overline{\gamma}_t) + (1-\overline{\gamma}_t) \gamma_{t+1} \\ &= 1 - (1 - \overline{\gamma}_t) (1 - \gamma_{t+1}) \\ &= 1 - (1 - \overline{\gamma}_{t+1}) \\ &= \overline{\gamma}_{t+1} \\ \end{aligned} $$ $x \ne x_0$이고 $x \ne K + 1$일 때, $$ \begin{aligned} Q_{t+1} v(x_0)_{(x)} &= \overline{\beta}_t (\alpha_{t+1} + \beta_{t+1}) + \overline{\beta}_t \beta_{t+1} (K-1) + \overline{\alpha}_t \beta_{t+1} \\ &= \overline{\beta}_t (\alpha_{t+1} + K \beta_{t+1}) + \overline{\alpha}_t \beta_{t+1} \\ &= \frac{1 - \overline{\alpha}_t - \overline{\gamma}_t}{K} (1-\gamma_{t+1}) + \overline{\alpha}_t \beta_{t+1} \\ &= \frac{1}{K} (1-\overline{\gamma}_t)(1-\gamma_{t+1}) + \overline{\alpha}_t (\beta_{t+1} - \frac{1-\gamma_{t+1}}{K}) \\ &= \frac{1}{K} (1-\overline{\gamma}_{t+1}) + \overline{\alpha}_t (\frac{1 - \alpha_{t+1} - \gamma_{t+1}}{K} - \frac{1-\gamma_{t+1}}{K}) \\ &= \frac{1}{K} (1-\overline{\gamma}_{t+1}) - \frac{1}{K} \overline{\alpha}_t \alpha_{t+1} \\ &= \frac{1}{K} (1-\overline{\gamma}_{t+1} - \overline{\alpha}_{t+1}) \\ &= \overline{\beta}_{t+1} \end{aligned} $$ 따라서, 모든 $t$에 대하여 $\overline{Q}_t v(x_0) = \overline{\alpha}_t v(x_0) + (\overline{\gamma}_t - \overline{\beta}_t) v(K+1) + \overline{\beta}_t$가 성립한다.

---

여기서 $\overline{\alpha}_t$, $\overline{\gamma}_t$, $\overline{\beta}_t$는 사전에 계산하여 저장해둘 수 있다. 따라서 $q (x_t \vert x_0)$의 계산 비용이 $O(tK^2)$에서 $O(K)$로 줄어든다.

2. Learning the reverse process

Diffusion process를 reverse시키기 위해 denoising network $p_\theta (x_{t−1} \vert x_t, y)$를 학습하여 사후 확률 분포 $q(x{t−1} \vert x_t, x_0)$를 추정한다. 신경망은 다음 variational lower bound(VLB)을 최소화하도록 학습된다.

\[\begin{aligned} \mathcal{L}_{\textrm{vlb}} &= \mathcal{L}_{0} + \mathcal{L}_{1} + \cdots + \mathcal{L}_{T-1} + \mathcal{L}_{T} \\ \mathcal{L}_{0} &= -\log p_\theta (x_0 | x_1, y) \\ \mathcal{L}_{t-1} &= D_{KL} (q(x_{t-1} | x_t, x_0) \; \| \; p_\theta (x_{t-1} | x_t, y)) \\ \mathcal{L}_{T} &= D_{KL} (q(x_T | x_0) \; \| \; p(x_T)) \end{aligned}\]

$p(x_T)$는 timestep $T$에서의 사전 확률(prior)이다. Mask-and-replace diffusion의 경우 사전 확률은 다음과 같다.

\[\begin{equation} p(x_T) = [ \overline{\beta}_T, \overline{\beta}_T, \cdots, \overline{\beta}_T, \overline{\gamma}_T ]^\top \end{equation}\]

Transition matrix $Q_t$가 학습 중에 고정되기 때문에 $\mathcal{L}_T$는 학습과 inference 사이의 차이를 측정하는 상수이고, 학습 중에 무시할 수 있다.

Reparameterization trick on discrete stage

네트워크 reparameterization는 합성 품질에 상당한 영향을 미친다. 최근 연구들에서는 사후 확률 $q(x_{t−1} \vert x_t, x_0)$를 직접 예측하는 대신 noise가 없는 target data $q(x_0)$와 같은 일부 대리 변수(surrogate variables)를 근사화하는 것이 더 품질이 낫다는 것을 발견했다. Discrete setting에서 네트워크가 각 reverse step에서 noise가 없는 토큰 분포 $p_\theta (\tilde{x}_0 \vert x_t, y)$를 예측하도록 한다. 따라서 다음과 같이 reverse transition distribution을 계산할 수 있다.

\[\begin{equation} p_\theta (x_{t-1} | x_t, y) = \sum_{\tilde{x}_0 = 1}^K q(x_{t-1} | x_t, \tilde{x}_0) p_\theta (\tilde{x}_0 | x_t, y) \end{equation}\]

Reparameterization trick에 기반하여 네트워크가 noise가 없는 토큰 $x_0$를 예측하도록 auxiliary denoising objective를 다음과 같이 정의한다.

\[\begin{equation} \mathcal{L}_{x_0} = -\log p_\theta (x_0 | x_t, y) \end{equation}\]

이 loss를 $\mathcal{L}_{\textrm{vlb}}$와 함께 사용하면 이미지 품질을 향상시킬 수 있다.

Model architecture

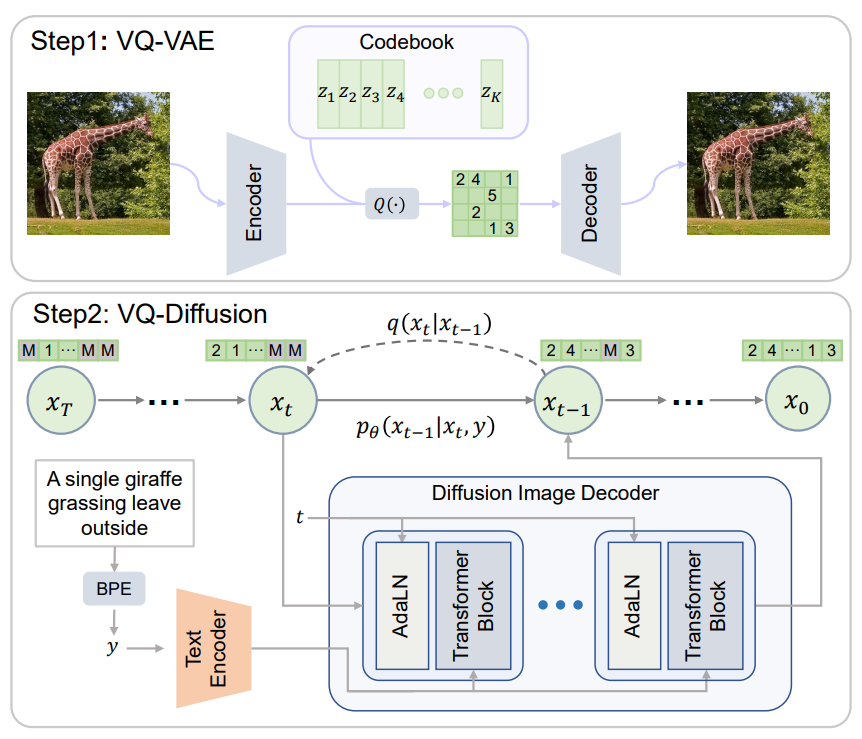
저자들은 분포 \(p_\theta (\tilde{x}_0 \vert x_t, y)\)를 추정하기 위해 인코더-디코더 transformer를 제안한다. 위 그림에서 볼 수 있듯이 프레임워크에는 text encoder와 diffusion image decoder의 두 부분으로 되어 있다. Text encoder는 텍스트 토큰 $y$를 취하고 조건부 feature 시퀀스를 생성한다. Diffusion image decoder는 이미지 토큰 $x_t$와 timestep $t$를 취하여 noise가 없는 토큰 분포 $p_\theta (\tilde{x}_0 \vert x_t, y)$를 출력한다. 디코더에는 여러 transformer 블록과 softmax layer가 포함되어 있다. 각 transformer 블록에는 full attention, 텍스트 정보를 결합하기 위한 cross attention, feed forward network 블록이 포함된다. 현재 timestep $t$는 Adaptive Layer Normalization (AdaLN) 연산자를 사용하여 네트워크에 주입된다.

\[\begin{equation} \textrm{AdaLN}(h, t) = a_t \textrm{LayerNorm}(h) + b_t \end{equation}\]

여기서 $h$는 intermediate activation이며, $a_t$ 와 $b_t$는 timestep embedding을 linear projection하여 얻는다.

Fast inference strategy

Inference 단계에서 reparameterization trick을 활용하여 더 빠른 inference를 달성하기 위해 diffusion model의 일부 step들을 건너뛸 수 있다. Time stride를 $\Delta_t$라 했을 때, $x_T, x_{T-1}, x_{T-2}, \cdots, x_0$로 샘플링하는 대신 $x_T, x_{T-\Delta_t}, x_{T-2\Delta_t}, \cdots, x_0$로 샘플링하며, 다음과 같은 reverse transition distribution을 사용한다.

\[\begin{equation} p_\theta (x_{t-\Delta_t} | x_t, y) = \sum_{\tilde{x}_0 = 1}^K q(x_{t-\Delta_t} | x_t, \tilde{x}_0) p_\theta (\tilde{x}_0 | x_t, y) \end{equation}\]

이 샘플링 방법을 사용하면 품질이 조금 떨어지지만 샘플링이 더 효율적이다. 전체 학습과 inference 알고리즘은 아래와 같다.

 

Experiments

• 데이터셋: CUB-200, Oxford-102, MSCOCO, CC3M, CC12M, LAION-400M
• Trianing details:
  • VQ-VAE의 인코더와 디코더는 VQGAN의 세팅과 동일
  • Text encoder는 CLIP model의 tokenizer 사용 (길이 77)
  • VQ-Diffusion-S는 192 차원의 18개의 transformer block (파라미터 약 3,400만개)
  • VQ-Diffusion-B는 1024 차원의 19개의 transformer block (파라미터 약 3.7억개)
  • VQ-Diffusion-F는 CC3M과 CC12로 학습한 VQ-Diffusion-B를 fine-tune
  • Timestep $T = 100$, loss weight $\lambda = 0.0005$
  • $\overline{\gamma}_t$는 0에서 0.9로, $\overline{\beta}_t$는 0에서 0.1로 선형적으로 증가
  • Optimizer는 AdamW ($\beta_1 = 0.9, \beta_2 = 0.96$), lr = 0.00045 (5000 iter warmup)

1. Comparison with state-of-the-art methods

다음은 text-to-image 합성에 대한 FID에 대한 표이다.

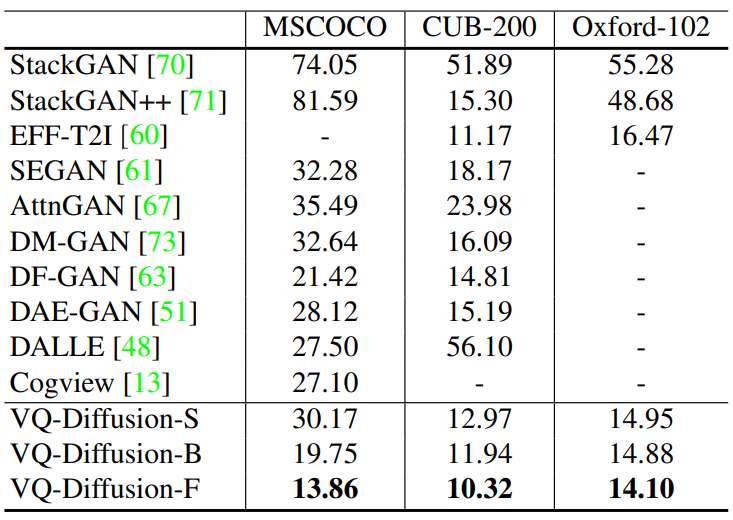
다음은 CUB-200과 MSCOCO에 대한 GAN 기반의 모델과의 비교 결과이다.

2. In the wild text-to-image synthesis

다음은 in-the-wild 이미지 생성 능력에 대한 결과이다.

VQ-Diffusion 모델은 DALL-E와 CogView보다 성능은 좋고 모델 크기는 작다.

3. Ablations

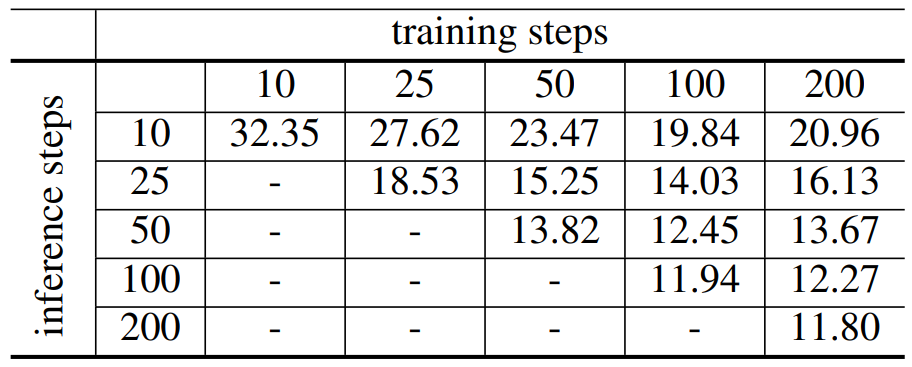
Number of timesteps

다음은 CUB-200 데이터셋에서 실험한 결과로 inference step 수와 학습 step 수에 따른 샘플의 FID에 대한 표이다.

Mask-and-replace diffusion strategy.

저자들은 Oxford-102 데이터셋으로 마지막 mask rate $\overline{\gamma}_T$를 다르게 설정하여 mask-and-replace 전략이 성능에 주는 이점을 확인하였다. 결과는 다음과 같다.

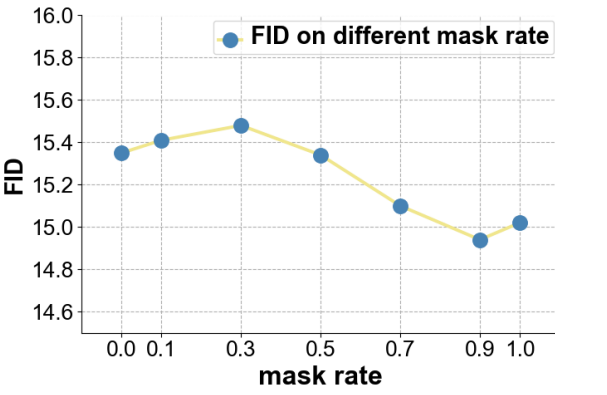
Mask rate가 0.9일 때 성능이 가장 좋았으며, 0.9보다 크면 오차 누적문제가 발생할 수 있고 0.9보다 작으면 모델이 어떤 부분에 더 많은 관심을 기울여야 하는지 찾기 어려울 수 있다.

Truncation

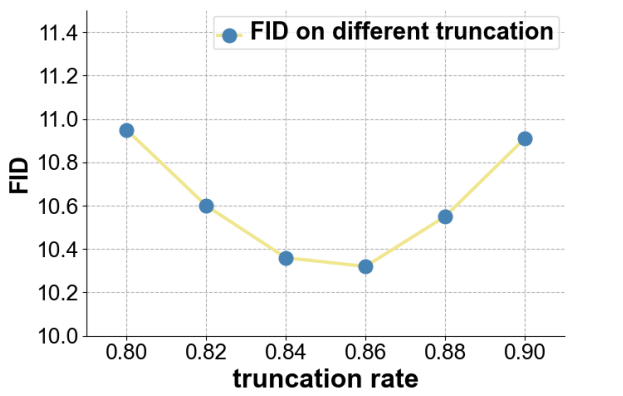
Truncation sampling 전략은 truncation rate가 $r$일 때 inference 단계에서 $p_\theta(\tilde{x}_0 \vert x_t, y)$의 상위 $r$만큼의 토큰만 남겨두는 전략이다. 낮은 확률의 토큰으로부터 샘플링되는 것을 막을 수 있기 때문에 VQ-Diffusion 모델에 굉장히 중요하다. 저자들은 CUB-200 데이터셋에서 서로 다른 $r$에 대해 어떤 결과가 나타나는지 실험하였다.

VQ-Diffusion vs VQ-AR

공정한 비교를 위하여 diffusion image decoder만 autoregressive decoder로 바꾼 VQ-AR-S, VQ-AR-B의 성능을 CUB-200 데이터셋에 대하여 확인하였다. 결과는 다음과 같다.

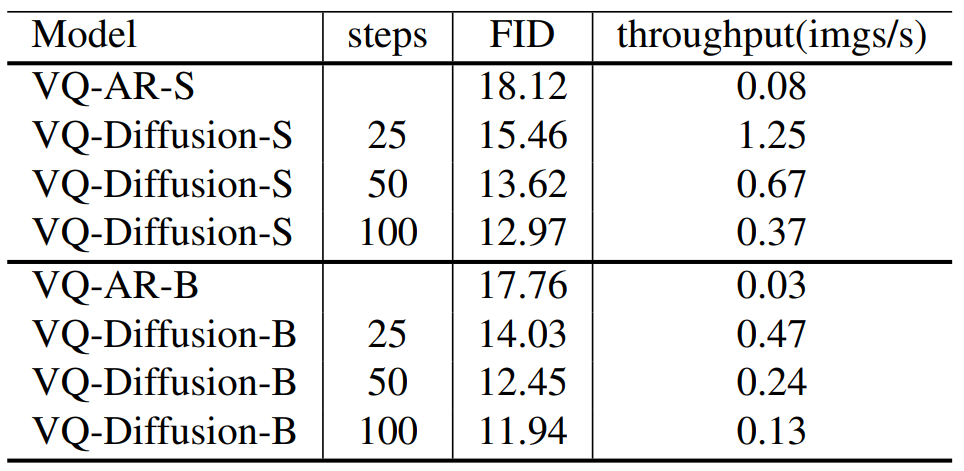
Throughput은 V100 GPU에서 배치 사이즈 32로 실험한 결과이다. VQ-Diffusion이 VQ-AR보다 15배 빠르며 FID도 더 낮았다.

4. Unified generation model

VQ-Diffusion 방법은 unconditional synthesis이나 class-conditional synthesis와 같은 다른 이미지 합성 task에도 적용할 수 있다.

클래스 label로부터 이미지를 생성하기 위해 먼저 text encoder network와 transformer의 cross attention 부분을 제거하였으며 클래스 label을 AdaIN 연산자로 주입하였다. 모델은 512 차원의 24개의 transformer block으로 구성되며 ImageNet로 학습되었다. VQ-VAE는 ImageNet에서 학습된 VQ-GAN의 모델을 사용하였다.

다음은 ImageNet에 대한 class-conditional synthesis와 FFHQ에 대한 unconditional synthesis 결과이다.

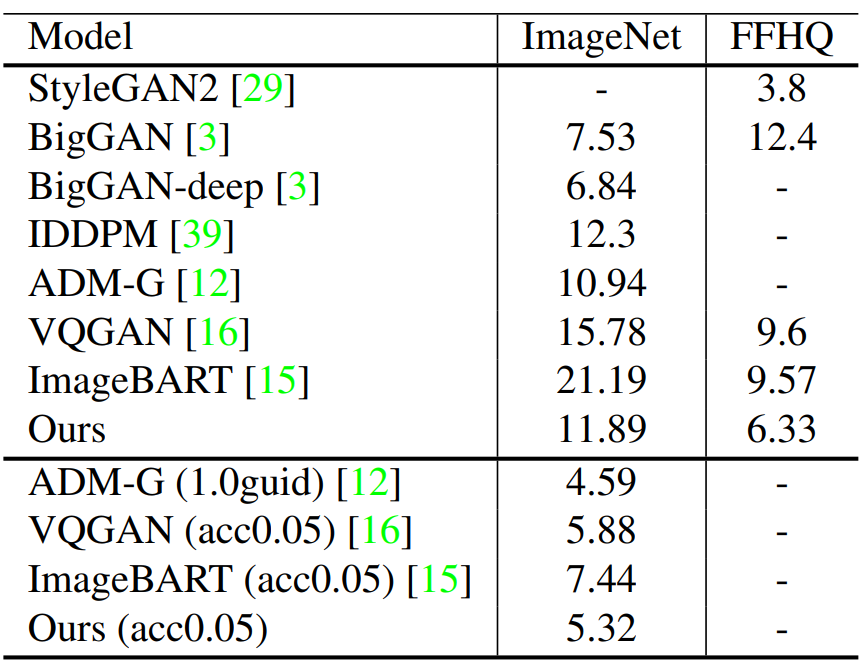
‘guid’는 classifier guidance를 사용했다는 것이며, ‘acc’는 adopting acceptance rate이다.

5. Irregular mask inpainting

마스크 외의 부분도 약간의 변화가 있지만 굉장히 inpainting이 잘 되었다. 마스크 외의 부분은 원본 이미지를 그대로 사용하면 되기 때문에 큰 문제는 되지 않을 것 같다.