[논문리뷰] ViPE: Video Pose Engine for Geometric 3D Perception

arXiv 2025. [Paper] [Page] [Github]
Jiahui Huang, Qunjie Zhou, Hesam Rabeti, Aleksandr Korovko, Huan Ling, Xuanchi Ren, Tianchang Shen, Jun Gao, Dmitry Slepichev, Chen-Hsuan Lin, Jiawei Ren, Kevin Xie, Joydeep Biswas, Laura Leal-Taixe, Sanja Fidler
NVIDIA
12 Aug 2025

Introduction

기존의 SLAM 시스템은 시간적 일관성과 loop closure를 활용하여 긴 동영상 시퀀스에서 카메라 포즈와 sparse geometry를 추정하는 데 탁월하다. 그러나 일반적으로 정적 장면과 알려진 카메라 intrinsic을 가정하며, 동적 물체나 degenerate motion에는 취약할 수 있다. COLMAP과 같은 일부 시스템은 intrinsic을 개선할 수 있지만, 다양한 동영상에 대해 dense geometry와 함께 이를 최적화하는 것은 여전히 어려운 과제이다.

최근에는 대용량 데이터셋을 학습하여 이미지에서 카메라 포즈와 깊이를 직접 예측하는 end-to-end feed-forward 모델이 등장했다. 이러한 모델들은 뛰어난 robustness를 보여주지만, scalability에 한계가 있다. 긴 동영상 처리는 GPU 메모리 사용량이 많아 처리가 어려운 경우가 많아, 동영상 프레임을 서브샘플링하거나 짧고 분리된 청크를 처리하는 방법을 사용해야 한다. 최근 유망한 추세는 MASt3R와 같은 강력한 학습된 프런트엔드를 기존 SLAM 백엔드에 통합하여 SLAM과 feed-forward 방식을 혼합한 하이브리드 방식을 모색하는 것이다. 그러나 단순히 프런트엔드를 교체하는 것만으로는 실제로 충분하지 않은 경우가 많다.

본 논문에서는 기존 방식과 학습 기반 방식 간의 격차를 해소하기 위해 설계된 Video Pose Engine (ViPE)을 소개한다. ViPE는 SLAM과 유사한 dense bundle adjustment (BA) 프레임워크의 scalability와 정밀도에 최신 학습 구성 요소의 robustness를 결합하였다. 이러한 시너지 효과를 통해 ViPE는 까다로운 실제 환경에서 촬영된 동영상에서 카메라 포즈, intrinsic, dense metric depth map을 정확하고 효율적으로 추정할 수 있다. 또한 ViPE는 프레임별 최적화가 필요하지 않아 더욱 효율적이다. 동적 물체를 처리하기 위한 더욱 robust한 전략이 제시되었으며, 다양한 카메라 모델이 지원된다. 속도 측면에서는 일반적으로 GPU 1개에서 3~5FPS의 속도에 도달할 수 있다.

Method

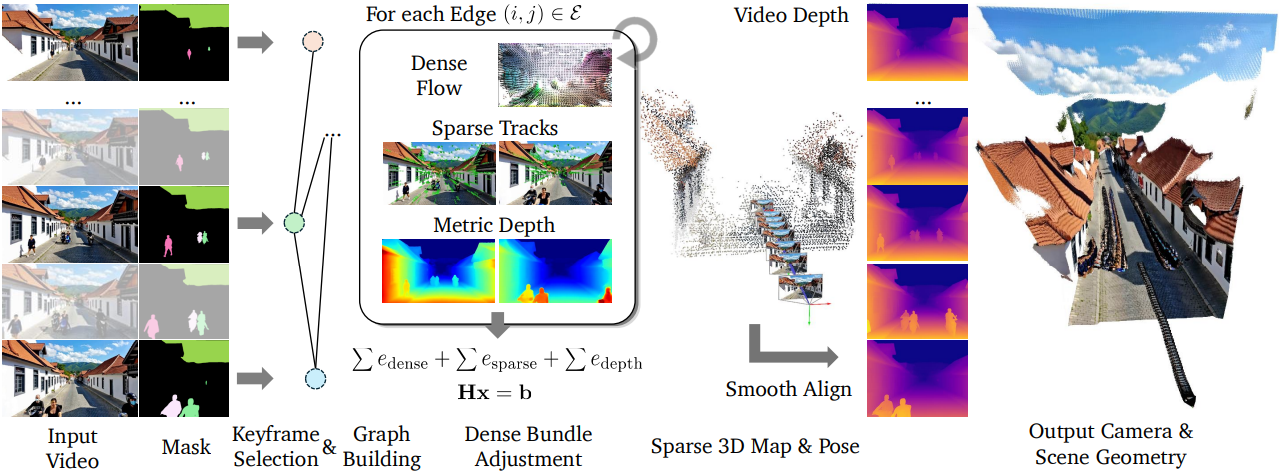
1. Overview

ViPE의 파이프라인은 키프레임 기반 SLAM 시스템을 기반으로 하여 임의 길이의 동영상에 대한 scalability와 robustness를 향상시켰다. 일반적으로 대부분의 키프레임 기반 시스템과 동일한 프런트엔드 및 백엔드 설계를 따르며, 다음과 같은 단계들로 구성된다.

Intrinsic 초기화: 카메라 intrinsic에 대한 초기 추정치는 동영상에서 4개 프레임을 균일하게 샘플링하고 GeoCalib을 통해 얻는다.
키프레임 선택: 각 입력 프레임에 대해 현재 프레임에서 이전 키프레임까지의 모션을 예측한다. 이 모션은 dense flow network와 sparse keypoint track의 가중 조합으로 구한 optical flow이다. 모션이 미리 정의된 threshold보다 크면 이를 키프레임으로 간주하여 Bundle Adjustment (BA) 그래프 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$에 추가한다.
프런트엔드 트래킹: 새로 추가된 키프레임에 대해, 마지막 여러 키프레임의 작은 sliding window 내에 그래프 $\mathcal{G}$를 구축한다. 이 window 내의 프레임들은 관측 시간 간격이 가깝거나 co-visibility가 충분히 높은 경우 edge로 연결된다. 그런 다음 에너지 방정식을 구성하고 Gauss-Newton solver를 사용하여 최적화한다.
백엔드 최적화: 백엔드에서는 현재 모든 키프레임을 포함하는 전체 BA 최적화 문제를 해결하고, $\mathcal{G}$는 위와 유사하게 구축한다. 이 단계에서는 카메라 intrinsic도 최적화를 위해 잠금 해제된다. 키프레임 수가 8, 16, 64개에 도달할 때와 프런트엔드 트래킹이 끝날 때 이 최적화를 수행한다.
포즈 채우기: 각 키프레임이 아닌 프레임에 대해, 해당 프레임을 가장 가까운 두 키프레임에 연결하는 작은 로컬 그래프를 구축하여 포즈를 구한다. 키프레임에서 키프레임이 아닌 프레임으로만 단방향 edge를 추가하여 BA 최적화 과정에서 모든 프레임에 대한 metric depth를 계산할 필요성을 제거한다. 이 절차는 키프레임이 아닌 모든 프레임에 병렬로 적용된다.
Dense depth map 추정: 각 프레임에 대해 카메라 포즈와 intrinsic과 일치하는 입력 이미지와 동일한 해상도의 dense depth map을 추정한다.

2. Formulation

ViPE의 핵심은 그래프 $\mathcal{G}$의 각 키프레임 $i$에 대하여, 프레임 포즈 $\{\textbf{T}_i \in \mathbb{SE}(3)\}$, 카메라 intrinsic $\textbf{k} \in \mathbb{R}^K$, 저해상도 depth map $\{\textbf{D}_i \in \mathbb{R}^{h \times w}\}$를 변수로 두고 BA 문제를 해결하는 것이다.

\[\begin{equation} e_\textrm{ViPE} (\{\textbf{T}_i\}, \{\textbf{D}_i\}, \textbf{k}) = \sum_{(i, j) \in \mathcal{E}} e_\textrm{dense} (\textbf{T}_i, \textbf{T}_j, \textbf{D}_i, \textbf{k}) + \sum_{(i, j) \in \mathcal{E}} e_\textrm{sparse} (\textbf{T}_i, \textbf{T}_j, \textbf{D}_i, \textbf{k}) + \sum_{i \in \mathcal{V}} e_\textrm{depth} (\textbf{D}_i) \end{equation}\]

여기서 $e_\textrm{dense}$는 두 프레임 사이의 dense matching을 활용하는 항, $e_\textrm{sparse}$는 sparse keypoint matching 정보를 활용하는 항, $e_\textrm{depth}$는 포즈 추정의 일관성과 robustness를 보장하기 위한 깊이 정규화 항이다. 에너지 함수 $e_\textrm{ViPE}$는 Gauss-Newton solver를 사용하여 최소화되며, 선형 시스템은 본질적으로 sparse하므로 COLAMD reordering을 사용하는 factorized solver로 효율적으로 해결할 수 있다.

2.1. Dense Flow Constraint

Dense flow 제약 조건은 DROID-SLAM과 동일하다.

\[\begin{equation} e_\textrm{dense} (\textbf{T}_i, \textbf{T}_j, \textbf{D}_i, \textbf{k}) = \sum_{\textbf{u}} w[\textbf{u}] \cdot \| \Pi_\textbf{k} (\textbf{T}_j^{-1} \textbf{T}_i \odot \Pi_\textbf{k}^{-1} (\textbf{D}_i [\textbf{u}])) - \textbf{u} - \textbf{F}_{ij} [\textbf{u}] \|^2 \end{equation}\]

($\textbf{u}$는 이미지의 픽셀 좌표, $\textbf{F}_{ij} \in \mathbb{R}^{h \times w \times 2}$는 optical flow 모델로 추정한 optical flow map)

Depth map $\textbf{D}$에 존재하는 모든 $h \times w$ 픽셀에 대해 합산되며, 최적화할 변수의 수를 줄이기 위해 $h = H/8$, $w = W/8$을 선택한다. Flow 추정의 신뢰도와 모션 확률을 반영하기 위해 가중치 맵 $w$도 추정된다.

2.2. Sparse Point Constraint

추정된 dense optical flow $\textbf{F}_{ij}$는 다양한 카메라 모션과 텍스처가 없는 장면에 robust하지만, 저해상도와 네트워크 추론 특성으로 인해 localization에 중요한 원본 고해상도 이미지에서만 볼 수 있는 미세한 디테일을 놓칠 수 있다. 이를 염두에 두고, cuVSLAM 패키지의 CUDA 기반 고속 feature detection 및 tracking 모듈을 기반으로 하는 sparse point 제약 조건을 추가로 사용한다. Feature는 원본 고해상도 이미지에서 계산되어 네트워크 해상도에 대한 하위 픽셀 제약 조건을 제공하므로 물리적으로 근거가 있는 정확한 flow를 제공한다. Sparse 제약 조건은 다음과 같다.

\[\begin{equation} e_\textrm{sparse} (\textbf{T}_i, \textbf{T}_j, \textbf{D}_i, \textbf{k}) = \sum_{\textbf{p}_i} \| \Pi_\textbf{k} (\textbf{T}_j^{-1} \textbf{T}_i \odot \Pi_\textbf{k}^{-1} (\textrm{Bilerp}(\textbf{D}_i, \textbf{p}_i))) - \textbf{p}_j \|^2 \end{equation}\]

($\textbf{p}_i \in \mathbb{R}^2$와 $\textbf{p}_j \in \mathbb{R}^2$는 각각 프레임 $i$와 $j$에서 매칭된 sparse keypoint이고, $\textrm{Bilerp}(\textbf{D}_i, \textbf{p}_i)$는 $\textbf{p}_i$에서 depth map의 bilinear interpolation)

그러나 한 $e_\textrm{sparse}$ 항의 Jacobian은 $\textbf{D}$의 최대 4개의 픽셀 위치와 관련되어 $\mathcal{G}$ 자체의 depth map 간에 수많은 상호 작용을 생성하며, 실제로 BA 문제를 풀 때 semi-sparse Hessian 패턴을 초래한다. 따라서 저자들은 bilinear interpolation보다 더 간단한 bilinear splatting 연산으로 대체하였다.

\[\begin{equation} e_\textrm{sparse} (\textbf{T}_i, \textbf{T}_j, \textbf{D}_i, \textbf{k}) = \sum_{\textbf{p}_i} \| \Pi_\textbf{k} (\textbf{T}_j^{-1} \textbf{T}_i \odot \Pi_\textbf{k}^{-1} (\textrm{Bisplat}(\{\textbf{p}_j - \textbf{p}_i\}, \{\textbf{p}_i\}))) - \textbf{p}_j \|^2 \end{equation}\]

Bilinear splatting은 각 픽셀 위치 $\textbf{u}$에 모든 입력 위치 $\textbf{p}_i$까지의 거리로 가중치가 적용된 누적 값을 할당하는 연산이다.

2.3. Depth Regularization

Flow correspondence와 마찬가지로, 정확한 depth map 추정은 모호성 해결에 필수적이며, 특히 작은 카메라 모션의 경우 더욱 그렇다. 따라서 다음과 같은 깊이 정규화 항을 추가한다.

\[\begin{equation} e_\textrm{depth} (\textbf{D}_i) = \sum_{\textbf{u}} m[\textbf{u}] \cdot \| \textbf{D}_i [\textbf{u}] - \textbf{D}_i^\textrm{prior} [\textbf{u}] \|^2 \end{equation}\]

($\textbf{D}_i^\textrm{prior}$는 사전 학습된 monocular metric depth estimation 네트워크에서 추정된 depth map, $m$은 깊이 불확실성)

카메라 모델에 따라 다양한 depth estimation 모델 중에서 선택할 수 있다. Depth estimation 모델은 단일 이미지를 기반으로 하며 현재 장면의 스케일을 추정한다. 따라서 SLAM 시스템에서 흔히 발생하는 scale drifting 문제를 줄이는 데 도움이 될 뿐만 아니라 실제 metric scale에 대한 정확한 추정치도 제공한다.

특히, metric depth estimation 모델의 경우, 예측된 depth map은 카메라 intrinsic $\textbf{k}$에 따라 결정된다. 따라서 intrinsic이 최적화된 후 깊이 예측을 업데이트하고, 이전 depth map $\textbf{D}_i^\textrm{prior}$를 새로 예측된 depth map으로 대체한다.

2.4. Dynamic Object Masking

많은 실제 동영상은 일반적으로 동영상의 넓은 픽셀 영역을 차지하는 동적 물체를 포함하고 있어, 카메라 포즈 $\textbf{T}$가 의존하는 정적 배경을 결정하는 까다로운 모호성을 가지고 있다. 본 논문에서는 robustness와 효율성을 위해 순수 semantic segmentation 정보를 사용하는 간단한 접근 방식을 사용하였다. 구체적으로, semantic 클래스 목록이 주어지면, 먼저 GroundingDINO를 적용하여 bounding box를 얻고 Segment Anything 모델에 프롬프트로 제공하여 이러한 클래스의 segmentation mask를 얻는다. 각 프레임에 이 두 모델을 적용하는 대신, 고정된 프레임 간격에 두 모델을 적용하고 XMem을 통해 segmentation mask를 전파한다.

Semantic mask의 출력을 반전하여 정적 배경 마스크 $\textbf{M}$을 얻는다. $e_\textrm{dense}$의 경우, $\textbf{M}$에 dense flow network로 예측한 가중치를 곱하여 가중치 맵 $w$를 얻는다. 마찬가지로 $e_\textrm{sparse}$의 경우 $\textbf{M}$ 외부의 모든 point track을 제거하고 이를 outlier로 처리한다.

2.5. Handling Different Camera Models

ViPE는 다양한 카메라 모델을 지원하고 각 카메라의 intrinsic $\textbf{k}$를 최적화한다. 본 시스템은 다음과 같은 radial camera를 가정하여 구축되었다.

\[\begin{equation} \textbf{u} = \Pi_\textbf{k} \left( \begin{bmatrix} x \\ y \\ z \end{bmatrix} \right) = \begin{bmatrix} f \cdot q_\textbf{k} (\theta) \cdot \cos \phi + W/2 \\ f \cdot q_\textbf{k} (\theta) \cdot \sin \phi + H/2 \end{bmatrix} \\ \textrm{where} \quad \theta = \textrm{arctan} \frac{\sqrt{x^2 + y^2}}{z}, \quad \phi = \textrm{arctan} \frac{y}{x} \end{equation}\]

($x$, $y$, $z$는 카메라 공간에서의 3D 좌표, 단순화를 위해 principal point는 항상 이미지 중심에 고정하고 초점 거리 $f$는 두 축에서 동일하다고 가정)

간단한 핀홀 카메라의 경우, $\textbf{q}_\textbf{k} (\theta) = \tan \theta$로 두고, $f$는 $\textbf{k}$에서 추정되는 스칼라 파라미터이다. 광각/fisheye 카메라의 경우, $\textbf{q}_\textbf{k} (\theta) = \frac{\tan \theta}{1 + \alpha \sqrt{\tan^2 \theta + 1}}$이고 $\textbf{k} = [f, \alpha] \in \mathbb{R}^2$인 통합 카메라 모델을 따른다. 여기서 $\alpha$는 왜곡 강도를 제어하며, $\alpha = 0$일 경우 핀홀 카메라 모델과 동일하다.

$\textbf{T}_i$를 $\textbf{T}_v \textbf{T}_i$로 확장하면 멀티 카메라 리그로 BA 기반 공식을 확장할 수 있다. 여기서 $\textbf{T}_v$는 리그에서 $v$번째 카메라의 레퍼런스 프레임으로의 변환이다. 360 카메라는 원본 이미지를 6개의 핀홀 카메라에 projection하고, 최적화 중에 상대적 변환 $\textbf{T}_v$를 고정한다.

카메라의 view frustum이 거의 겹치지 않으면 co-visibility 랜드마크를 찾는 데 덜 효과적일 수 있다. 따라서 dense depth map을 다른 카메라의 뷰에 projection하여 측정한 카메라의 co-visibility를 기반으로 그래프에 edge를 적응적으로 추가한다.

3. Post-processed Dense Depth Alignment

SOTA depth estimation 모델은 고품질의 relative depth map을 생성할 수 있지만, 전체 동영상 시퀀스에서 추정된 카메라 포즈 $\{\textbf{T}_i\}$를 사용하여 일관된 absolute scale을 복구하는 것은 어렵다. 반면, BA 방정식을 통해 구한 dense depth map $\textbf{D}$는 일반적으로 카메라 포즈와 더 잘 정렬되며 전체 동영상 시퀀스에서 일관성을 보인다. 그러나 $\textbf{D}$는 노이즈가 많거나 불완전할 수 있으며 해상도가 낮을 수 있다.

저자들은 두 가지 장점을 모두 얻기 위해, 매끄러운 깊이 정렬 전략을 제안하였다. 먼저 동영상 depth estimation 모델을 사용하여 각 프레임 $i$에 대해 시간적으로 매끄럽지만 affine-invariant depth map $\textbf{D}_i^\textrm{VDA} \in \mathbb{R}^{H \times W}$을 추정한다. 동시에, BA 최적화에서 $\{\textbf{D}_i\}$를 unprojection하여 포인트 클라우드를 집계하고, 추정된 카메라 포즈와의 일관성 검사에 실패한 픽셀을 필터링한 후, 이미지 공간으로 다시 projection하여 sparse depth map $\textbf{D}_i^\textrm{BA} \in \mathbb{R}^{H \times W}$을 얻는다. 그런 다음, 모멘텀 기반 업데이트 전략을 사용하여 최적의 affine transformation 파라미터를 찾는다.

\[\begin{equation} \alpha_i, \beta_i = \underset{\alpha, \beta}{\arg \min} \sum_{\textbf{u} \; \textrm{is valid}} \| \textbf{M} \cdot (\alpha / \textbf{D}_i^\textrm{VDA} [\textbf{u}] + \beta - 1/\textbf{D}_i^\textrm{BA} [\textbf{u}]) \|_2^2 \end{equation}\]

($m$은 momentum factor, 최종 depth map은 $\textbf{D}_i^\textrm{HD} = \frac{1}{\hat{\alpha}_i / \textbf{D}_i^\textrm{VDA} + \hat{\beta}_i}$)

특히, 실제 동영상은 장면 분포 측면에서 다양할 수 있으며, projection된 depth map $\textbf{D}_i^\textrm{BA}$에는 위의 affine transformation을 제한할 만큼 충분한 정보가 없을 수 있다. 따라서 이 depth map에 포함되는 픽셀의 비율을 계산하고, 정렬을 위해 이를 $\textbf{D}_i^\textrm{BA}$에 할당하기 전에 부분 관측값과 입력 이미지를 조건으로 depth map을 채우는 PriorDA를 적용한다. 픽셀 중 일부만 포함되거나 전혀 포함되지 않는 매우 극단적이고 드문 경우에는 $\textbf{D}_i^\textrm{BA}$를 metric depth 추정값으로 직접 할당한다.

Experiments

1. Camera Pose Estimation

다음은 (위) TUM-RGBD 데이터셋과 (아래) 야외 운전 데이터셋에서의 포즈 및 intrinsic 정확도를 비교한 결과이다.

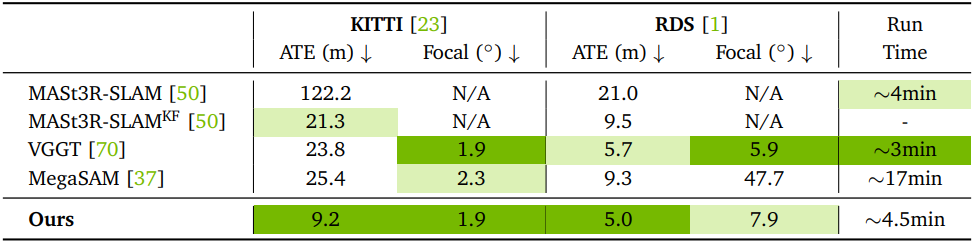
다음은 KITTI 데이터셋에서의 포즈 추정 결과를 정성적으로 비교한 것이다.

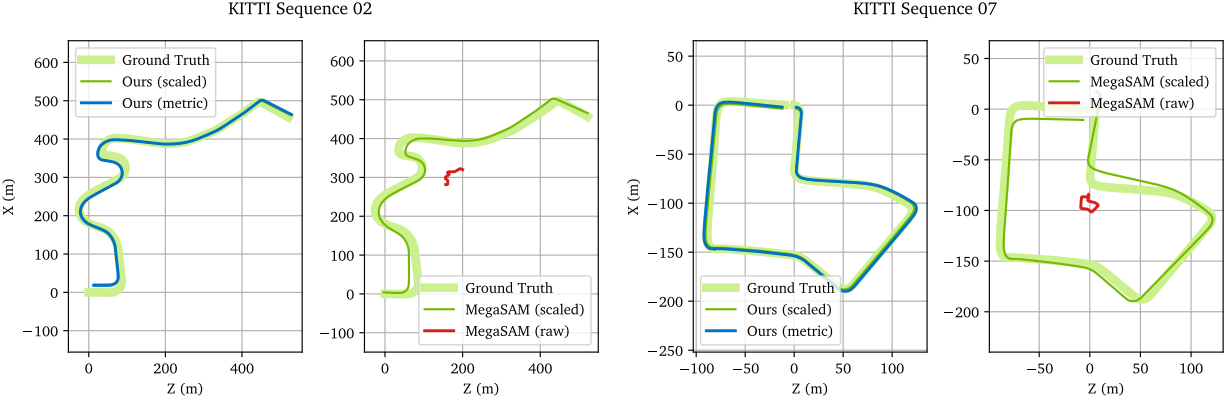
다음은 GT 포즈를 모르는 데이터셋에 대한 포즈 일관성을 비교한 결과이다.

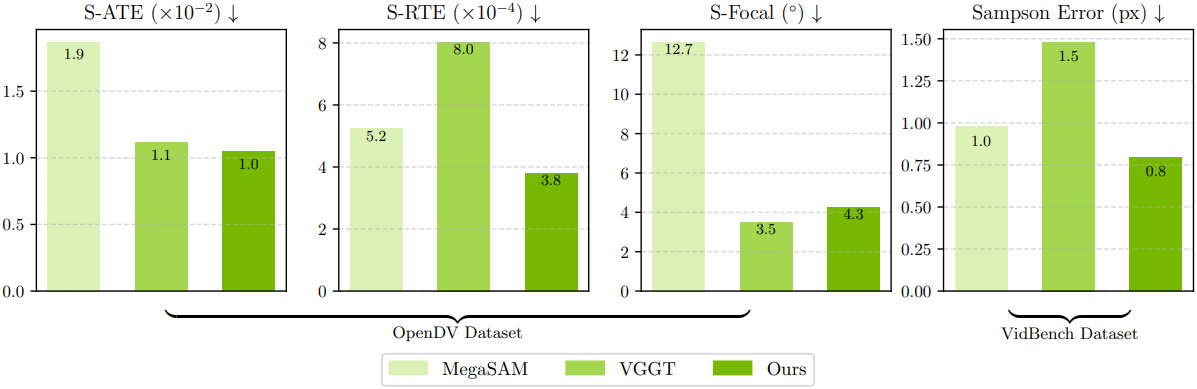
2. Depth Estimation

다음은 실내 장면에 대한 depth estimation 정확도를 비교한 결과이다.

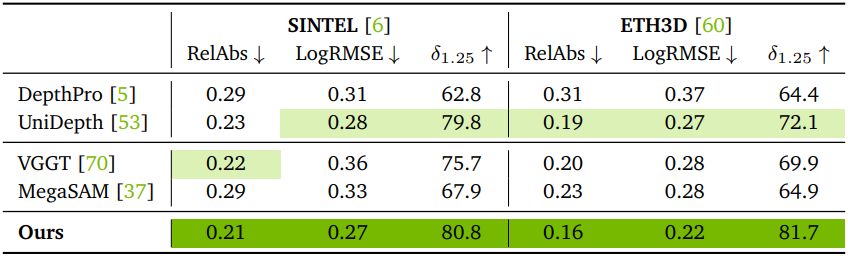
다음은 SINTEL 데이터셋에서 정량적으로 비교한 결과이다.

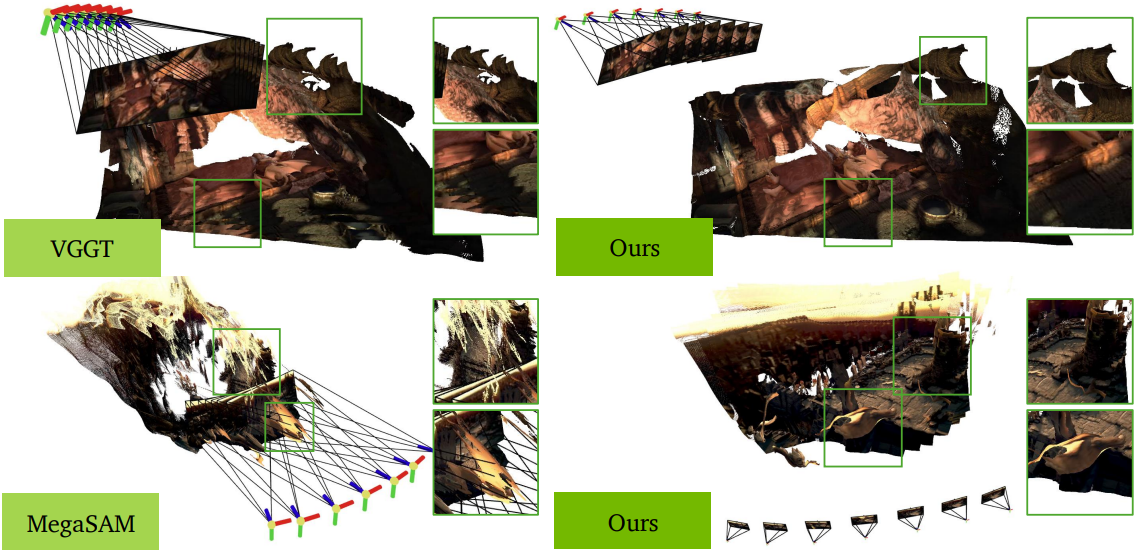
3. Ablation Study

다음은 ablation study 결과이다.

JiYeop Kim