[논문리뷰] ViewDiff: 3D-Consistent Image Generation with Text-to-Image Models

CVPR 2024. [Paper] [Page] [Github]
Lukas Höllein, Aljaž Božič, Norman Müller, David Novotny, Hung-Yu Tseng, Christian Richardt, Michael Zollhöfer, Matthias Nießner
Technical University of Munich | MIT EECS
4 Mar 2024

Introduction

본 논문에서는 사전 학습된 text-to-image (T2I) diffusion model의 2D prior를 활용하여 사실적이고 3D에서 일치하는 3D 에셋 렌더링을 생성하는 방법을 제안하였다. 입력은 원하는 렌더링된 이미지의 카메라 포즈와 함께 텍스트 설명 또는 이미지이다. 제안된 접근 방식은 한 번의 forward pass에서 동일한 물체의 여러 이미지를 생성한다. 또한 새로운 시점에서 더 많은 이미지를 렌더링할 수 있는 autoregressive한 생성 방식을 사용한다. 구체적으로 기존 U-Net 아키텍처에 projection layer와 cross-frame-attention layer를 도입하여 생성된 물체에 대한 명시적인 3D 지식을 인코딩한다. 이를 통해 사전 학습된 가중치에 인코딩된 대규모의 2D prior의 이점을 활용하면서 CO3D와 같은 실제 3D 데이터셋에서 T2I 모델을 fine-tuning할 수 있는 길을 열었다.

Method

1. 3D-Consistent Diffusion

Diffusion model은 데이터 $x_0 \sim q(x_0)$와 latent variable $x_{1:T} = x_1, \ldots, x_T$에 대한 확률 분포 $p_\theta (x_0) = \int p_\theta (x_{0:T}) dx_{1:T}$를 학습하는 생성 모델의 한 종류이다. 본 논문의 방법은 사전 학습된 T2I 모델을 기반으로 하며, 이는 추가 텍스트 조건 $c$를 갖는 diffusion model $p_\theta (x_0 \; \vert \; c)$이다. (앞으로는 조건 c를 생략)

서로 3D에서 일치하는 여러 이미지 $x_0^{0:N}$을 한 번에 생성하기 위해, 이들의 공동 확률 분포

\[\begin{equation} p_\theta (x_0^{0:N}) = \int p_\theta (x_{0:T}^{0:N}) dx_{1:T}^{0:N} \end{equation}\]

를 모델링한다. DDPM의 reverse process를 모든 이미지에 걸쳐 마르코프 체인으로 공동으로 적용하며, 이미지별로 샘플링한 Gaussian noise들의 세트 $p (x_T^{0:N})$에서 생성을 시작하여 하나의 이미지 세트 $p_\theta (x_0^{0:N})$를 생성한다.

\[\begin{equation} p_\theta (x_{0:T}^{0:N}) := p (x_T^{0:N}) \prod_{t=1}^T \prod_{n=0}^N p_\theta (x_{t-1}^n \; \vert \; x_t^{0:N}) \end{equation}\]

모든 이미지에서 공유되는 신경망 $\mu_\theta$를 통해 이미지별 평균 $\mu_\theta^n (x_t^{0:N}, t)$를 예측하여 샘플들의 noise를 점진적으로 제거한다.

\[\begin{equation} p_\theta (x_{t-1}^n \; \vert \; x_t^{0:N}) = \mathcal{N} (x_{t-1}; \mu_\theta^n (x_t^{0:N}, t), \sigma_t^2 \mathbf{I}) \end{equation}\]

중요한 점은 각 step에서 모델은 모든 이미지의 이전 상태 $x_t^{0:N}$를 사용한다는 것이다. 즉, 모델 예측 중에 이미지 간에 통신이 있다. $\mu_\theta$를 학습시키기 위해 forward process를 마르코프 체인으로 정의한다.

\[\begin{equation} q (x_{1:T}^{0:N} \; \vert \; x_0^{0:N}) = \prod_{t=1}^T \prod_{n=0}^N q (x_t^n \; \vert \; x_{t-1}^n) \\ \textrm{where} \quad q (x_t^n \; \vert \; x_{t-1}^n) = \mathcal{N} (x_t^n; \sqrt{1 - \beta_t} x_{t-1}^n, \beta_t \mathbf{I}) \end{equation}\]

$\beta_1, \ldots, \beta_T$는 고정된 variance schedule이다.

DDPM을 따라 $\mu_\theta$ 대신 noise predictor $\epsilon_\theta$를 학습시킨다. $\epsilon_\theta$는 다음과 같은 L2 loss로 학습된다.

\[\begin{equation} \mathbb{E}_{x_0^{0:N}, \epsilon^{0:N} \sim \mathcal{N} (\mathbf{0}, \mathbf{I}), n} [\| \epsilon^n - \epsilon_\theta^n (x_t^{0:N}, t) \|^2] \end{equation}\]

2. Augmentation of the U-Net architecture

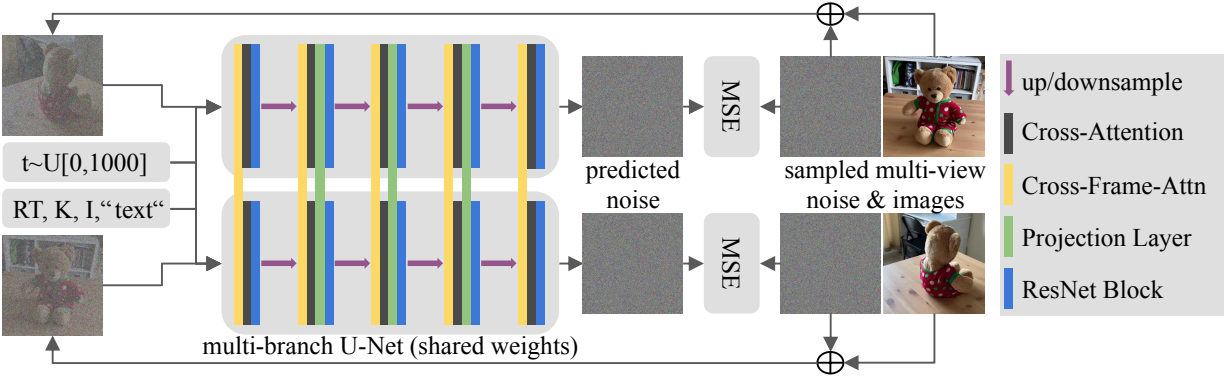
신경망 $\epsilon_\theta$를 통해 이미지별 noise $\epsilon_\theta^n (x_t^{0:N}, t)$를 예측한다. $\epsilon_\theta$는 기존 T2I 모델의 사전 학습된 가중치에서 초기화되며 일반적으로 U-Net 아키텍처로 정의된다. 모든 이미지의 이전 상태 $x_t^{0:N}$를 활용하여 3D에서 일관된 denoising step을 구성해야 한다. 이를 위해 U-Net 아키텍처에 cross-frame-attention layer와 projection layer를 추가한다. 모든 이미지가 별도의 Gaussian noise에서 시작하여 생성되므로 예측된 이미지별 noise는 이미지별이어야 한다. 따라서 기존 ResNet 및 ViT 블록을 fine-tuning하여 각 이미지에서 별도로 작동하는 약 2D 레이어를 유지하는 것이 중요하다.

Cross-Frame-Attention

동영상 diffusion model들(1, 2)에서 영감을 얻어 U-Net 아키텍처에 cross-frame-attention layer를 추가한다. 구체적으로 기존 self-attention layer를 수정하여

\[\begin{equation} \textrm{CFAttn} (Q, K, V) = \textrm{softmax} (\frac{QK^T}{\sqrt{d}}) V \\ \textrm{with} \quad Q = W^Q h_i, \quad W^K [h_j]_{j \ne i}, \quad V = W^V [h_j]_{j \ne i} \end{equation}\]

를 계산한다. 여기서 $W^Q$, $W^K$, $W^V$는 feature projection을 위해 사전 학습된 가중치이며, $h_i \in \mathbb{R}^{C \times H \times W}$는 각 이미지 $i$의 feature이다. Cross-frame-attention layer를 통해 모든 이미지들 사이의 feature들을 매칭하고 동일한 글로벌 스타일을 생성한다.

또한, 모든 cross-frame-attention layer와 cross-attention layer에 컨디셔닝 벡터를 추가하여 네트워크에 각 이미지의 시점에 대한 정보를 제공한다.

각 이미지의 카메라 행렬 $p \in \mathbb{R}^{4 \times 4}$를 $z_1 \in \mathbb{R}^4$에 인코딩하여 카메라 포즈 정보를 추가한다.
각 카메라의 focal length와 principal point를 임베딩 $z_2 \in \mathbb{R}^4$에 concatenate한다.
이미지 RGB 값의 평균과 분산을 $z_3 \in \mathbb{R}^2$에 저장한다. (intensity encoding)

학습 시에는 $z_3$를 각 입력 이미지의 실제 값으로 설정하고 테스트 시에는 모든 이미지에 대해 $z_3 = [0.5, 0]$로 설정한다. 이것은 데이터셋에 포함된 뷰에 따른 조명 차이를 줄이는 데 도움이 된다. 컨디셔닝 벡터를 $z = [z_1, z_2, z_3]$로 구성하고 LoRA-linear-layer $W^{\prime Q}$를 통해 feature projection layer $Q$에 추가한다.

\[\begin{equation} Q = W^Q h_i + W^{\prime Q} [h_i; z] \end{equation}\]

마찬가지로 $W^{\prime K}$와 $W^{\prime V}$를 통해 $K$와 $V$에 조건을 추가한다.

Projection Layer

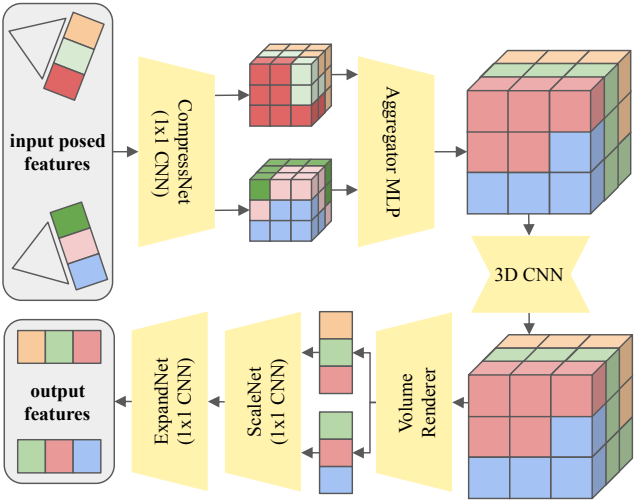
Cross-frame-attention layer는 3D에서 일관된 이미지를 생성하는 데 도움이 된다. 그러나 물체는 지정된 포즈를 정확하게 따르지 않아 뷰 불일치가 발생한다. 이를 위해 U-Net 아키텍처에 projection layer를 추가한다. 이 레이어의 아이디어는 다음 U-Net 레이어에서 추가로 처리되는 3D에서 일관된 feature를 만드는 것이다. U-Net의 모든 단계에서 이 레이어를 반복하여 이미지별 feature가 3D에서 일관되는지 확인한다. 첫 번째 및 마지막 U-Net 블록의 경우 projection layer를 추가하였을 때의 이점이 없으므로 추가하지 않는다. 이는 네트워크가 해당 단계에서 이미지별 정보를 처리하므로 3D 일관된 feature space가 필요하지 않기 때문이다.

Projection layer는 다음과 같이 작동한다.

모든 입력 feature $h_\textrm{in}^{0:N} \in \mathbb{R}^{C \times H \times W}$에서 3D feature voxel grid를 생성하고 각 voxel을 각 이미지 평면으로 projection한다.
1$\times$1 convolution으로 $h_\textrm{in}^{0:N}$을 축소된 feature 차원 $C^\prime = 16$으로 압축한다. 그런 다음 이미지 평면 위치에서 bilinearly interpolate된 feature를 가져와 voxel에 배치한다.
뷰별 voxel grid를 aggregator MLP를 통해 이를 하나의 grid로 병합한다. IBRNet에서 영감을 받아 MLP는 뷰별 가중치를 예측한 다음 feature의 가중 평균을 예측한다.
Voxel grid에서 작은 3D CNN을 실행하여 3D feature space를 정제한다.
NeRF와 유사한 볼륨 렌더링을 사용하여 voxel grid를 출력 feature $h_\textrm{out}^{0:N} \in \mathbb{R}^{C^\prime \times H \times W}$로 렌더링한다. Voxel grid의 절반을 전경에, 절반을 배경에 할당하고 ray-marching 중에 MERF의 배경 모델을 적용한다.
볼륨 렌더러는 ray-marching 중에 시그모이드를 최종 레이어로 사용하지만, 입력 feature는 임의의 부동 소수점 범위로 정의된다. $h_\textrm{out}^{0:N}$을 다시 같은 범위로 변환하기 위해 1$\times$1 convolution과 ReLU를 사용하여 feature를 비선형적으로 스케일링한다.
$h_\textrm{out}^{0:N}$을 입력 feature 차원 $C$로 확장한다.

3. Autoregressive Generation

학습하는 동안 $N = 5$로 설정하지만 inference 시에 메모리 제약 조건까지 (ex. $N = 30$) 늘릴 수 있다. 그러나 네트워크를 사용하여 가능한 모든 시점에서 물체를 렌더링하고자 한다. 이를 위해 autoregressive한 이미지 생성 방식을 사용한다. 즉, 이전에 생성된 이미지로 다음 시점의 생성을 컨디셔닝한다. 각 이미지의 timestep $t^{0:N}$을 U-Net의 입력으로 제공하며, $t^{0:N}$을 변화시킴으로써 다양한 유형의 컨디셔닝을 할 수 있다.

Unconditional Generation

모든 샘플은 Gaussian noise로 초기화되고 공동으로 denoising된다. Timestep $t^{0:N}$은 reverse process 전반에 걸쳐 모든 샘플에 대해 동일하게 유지된다. 하나의 텍스트 프롬프트와 이미지별 서로 다른 카메라를 제공한다.

Image-Conditional Generation

총 샘플 수 $N = n_c + n_g$를 조건부 부분 $n_c$와 생성 부분 $n_g$로 나눈다. 처음 $n_c$ 개의 샘플은 입력으로 제공된 이미지와 카메라에 해당한다. 다른 $n_g$개의 샘플은 조건부 이미지와 유사한 새로운 뷰를 생성해야 한다. $n_g$개의 샘플에 대해 Gaussian noise에서 생성을 시작하고 다른 샘플을 위해 noise가 없는 이미지를 제공한다. 마찬가지로, 모든 denoising step에 대해 $t^{0:n_c} = 0$으로 설정하고 $t^{n_g:N}$을 점진적으로 감소시킨다.

$n_c = 1$일 때, 단일 이미지 재구성을 수행한다. $n_c > 1$로 설정하면 이전 이미지에서 새로운 뷰를 autoregressive하게 생성할 수 있다. 실제로는 먼저 unconditional하게 이미지 batch 하나를 생성한 다음 이전 이미지의 부분집합으로 다음 atch를 컨디셔닝한다. 이를 통해 매끄러운 궤적으로 렌더링할 수 있다.

Results

데이터셋: CO3Dv2
- 카테고리: Teddybear, Hydrant, Apple, Donut
- 카테고리별로 500 ~ 1,000개의 object, 각 object당 200개의 이미지
- 해상도: 256$\times$256
구현 디테일
- voxel grid를 구축할 때 마지막 이미지는 생략
- fine-tuning
  - VAE 인코더와 디코더는 고정하고 U-Net만 fine-tuning
  - 확률 $p_1$ = 0.25와 $p_2$ = 0.25로 첫 번째 및/또는 두 번째 이미지를 입력으로 제공하고 해당 timestep을 0으로 설정
  - optimizer: AdamW
  - iteration: 60,000
  - 전체 batch size: 64
  - learning rate: 볼륨 렌더러만 0.005, 나머지 레이어는 $5 \times 10^{-5}$
  - GPU: NVIDIA A100 2개에서 약 7일 소요
- inference
  - batch당 30개의 이미지를 생성
  - GPU: RTX 3090 1개에서 약 15초 소요
  - sampler: UniPC (10 denoising step)

1. Unconditional Generation

첫 번째 batch는 guidance scale $\lambda_\textrm{cfg} = 7.5$로 $N = 10$개의 이미지를 생성한다. 그런 다음 나머지 batch들은 $\lambda_\textrm{cfg} = 0$로 설정하고 object당 총 100개의 이미지를 생성한다.

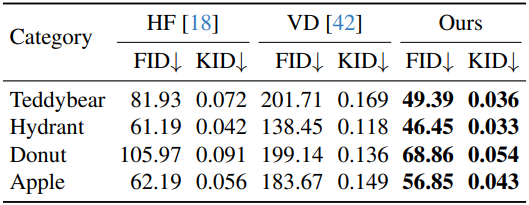
다음은 unconditional한 이미지 생성에 대한 결과를 HoloFusion (HF), ViewsetDiffusion (VD)과 비교한 것이다.

2. Single-Image Reconstruction

데이터셋에서 하나의 이미지를 샘플링하고, 역시 데이터셋에서 샘플링한 새로운 시점에서 20개의 이미지를 생성한다.

다음은 single-image reconstruction에 대하여 ViewsetDiffusion, DFM과 비교한 결과이다.

3. Ablations

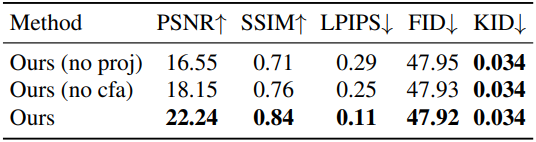
다음은 ablation 결과이다. (unconditional image generation)

다음은 생성된 여러 샘플들을 비교한 것이다.

Limitations

때때로 약간 불일치한 이미지를 생성한다. 모델은 뷰에 따른 효과를 가지는 실제 데이터셋에서 fine-tuning되므로 다양한 시점에서 이러한 변형을 생성하는 방법을 학습한다.
본 논문의 방법은 물체 중심의 장면에만 초점을 맞추고 있다.

JiYeop Kim