[논문리뷰] VideoFusion: Decomposed Diffusion Models for High-Quality Video Generation

CVPR 2023. [Paper]
Zhengxiong Luo, Dayou Chen, Yingya Zhang, Yan Huang, Liang Wang, Yujun Shen, Deli Zhao, Jingren Zhou, Tieniu Tan
University of Chinese Academy of Sciences | Alibaba Group | Ant Group | CRIPAC | CASIA | Nanjing University
15 Mar 2023

Introduction

Diffusion probabilistic model (DPM)은 데이터 포인트에 noise를 점진적으로 추가하는 diffusion process와 반복적인 denoising을 통해 새 샘플을 생성하는 denoising process로 구성된 심층 생성 모델 클래스이다. 최근 DPM은 고품질의 다양한 이미지를 생성하는 놀라운 성과를 거두었다.

이미지 생성에 대한 DPM의 성공에 영감을 받아 많은 연구자들이 유사한 아이디어를 동영상 예측/보간에 적용하려고 시도하고 있다. 동영상 생성을 위한 DPM에 대한 연구는 아직 초기 단계에 있으며 동영상 데이터가 더 높은 차원이고 복잡한 시공간 상관관계를 포함하기 때문에 어려움에 직면해 있다.

이전의 DPM 기반 동영상 생성 방법은 일반적으로 동일한 동영상의 프레임에 독립적인 noise가 추가되고 시간적 상관 관계도 noised latent 변수에서 점차 파괴되는 표준 diffusion process를 채택하였다. 결과적으로 동영상 생성 DPM은 denoising process에서 독립적인 noise 샘플로부터 일관된 프레임을 재구성해야 한다. 그러나 denoising network가 시시간적 상관 관계를 동시에 모델링하는 것은 상당히 어려운 일이다.

연속된 프레임이 대부분의 콘텐츠를 공유한다는 아이디어에 영감을 받아 저자들은 다음과 같은 생각을 하게 되었다.

일부 공통 부분이 있는 noise에서 동영상 프레임을 생성하는 것이 더 쉬울까?

본 논문은 이를 위해 표준 diffusion process를 수정하고 동영상 생성을 위해 VideoFusion이라는 분해된 DPM을 제안하였다. Diffusion process에서 프레임당 noise를 두 부분, 즉 base noise와 residual noise로 분해한다. 여기서 base noise는 연속 프레임에서 공유된다. 이러한 방식으로 서로 다른 프레임의 noised latent 변수는 항상 공통 부분을 공유하므로 denoising network가 일관된 동영상를 보다 쉽게 재구성할 수 있다.

직관적인 설명을 위해 DALL-E 2의 디코더를 사용하여 동일한 latent 임베딩을 조건으로 하는 이미지를 생성한다. 위 그림의 (a)에서와 같이 독립된 noise로부터 이미지를 생성하면 동일한 조건을 공유하더라도 그 내용이 많이 달라진다. 그러나 noised latent 변수가 동일한 base noise를 공유하는 경우 이미지 generator조차도 대략적으로 상관 관계가 있는 시퀀스를 합성할 수 있다 (위 그림의 (b) 참조). 따라서 동영상 생성 DPM의 denoising network 부담을 크게 경감할 수 있다.

또한, 이 분해된 공식은 추가적인 이점을 제공한다. 첫째, 기본 noise가 모든 프레임에서 공유되므로 하나의 프레임을 사전 학습된 대형 이미지 생성 DPM에 한 번의 forward pass로 공급하여 예측할 수 있다. 이러한 방식으로 사전 학습된 모델의 이미지 prior는 모든 프레임에서 효율적으로 공유될 수 있으므로 동영상 데이터 학습을 용이하게 할 수 있다. 둘째, base noise는 모든 동영상 프레임에서 공유되며 동영상 콘텐츠와 관련될 가능성이 높다. 이 속성을 사용하면 생성된 동영상의 콘텐츠 또는 동작을 더 잘 제어할 수 있다. 적절한 학습을 통해 VideoFusion은 base noise를 동영상 콘텐츠와 관련시키고 residual noise를 모션과 관련시키는 경향이 있다. VideoFusion은 다양한 데이터셋에서 SOTA 결과를 얻을 수 있고 텍스트 조건부 동영상 생성도 잘 지원할 수 있다.

Decomposed Diffusion Probabilistic Model

1. Standard Diffusion Process for Video Data

\(x = \{x_i \; \vert \; i = 1, 2, \ldots, N\}\)은 $N$ 프레임의 동영상 클립이고 \(z_t = \{z_t^i \; \vert \; i = 1, 2, \ldots, N\}\)은 step $t$에서 $x$의 noised latent 변수라고 하자. 그런 다음 $x^i$에서 $z_t^i$로의 전환은 다음과 같이 표현할 수 있다.

\[\begin{equation} z_t^i = \sqrt{\hat{\alpha}_t} x^i + \sqrt{1 - \hat{\alpha}_t} \epsilon_t^i, \quad \epsilon_t^i \sim \mathcal{N} (0, I) \end{equation}\]

이전 방법에서 각 프레임의 추가된 noise $\epsilon_\theta$는 서로 독립적이다. 그리고 동영상 클립 $x$의 프레임은 \(z_T \approx \{\epsilon_T^i \; \vert \; i = 1, 2, \ldots, N\}\)로 인코딩되며 각각은 독립적인 noise 샘플이다. 이 diffusion process는 동영상 프레임 간의 관계를 무시한다. 결과적으로 denoising process에서 denoising network는 이러한 독립적인 noise 샘플로부터 일관된 동영상을 재구성할 것으로 예상된다. 이 task는 충분히 강력한 denoising network에 의해 실현될 수 있지만 noise 샘플이 이미 상관된 경우 denoising network의 부담이 완화될 수 있다. 그러면 다음과 같은 질문이 생긴다.

Denoising process를 더 쉽게 만들기 위해 연속 프레임 간의 유사성을 활용할 수 있을까?

2. Decomposing the Diffusion Process

동영상 프레임 간의 유사성을 활용하기 위해 프레임 $x^i$를 기본 프레임 $x^0$와 나머지 $\Delta x^i$의 두 부분으로 나눈다.

\[\begin{equation} x^i = \sqrt{\lambda^i} x^0 + \sqrt{1 - \lambda^i} \Delta x^i, \quad i = 1, 2, \ldots N \end{equation}\]

여기서 $x^0$은 동영상 프레임의 공통 부분을 나타내고 $\lambda^i \in [0,1]$는 $x^i$에서 $x^0$의 비율을 나타낸다. 특히, $\lambda^i = 0$은 $x^i$가 $x^0$와 공통점이 없음을 나타내고, $λ^i = 1$은 $x^i = x^0$을 나타낸다. 이와 같이 동영상 프레임 간의 유사도는 $x^0$와 $\lambda^i$를 통해 파악할 수 있다. Step $t$에서 noised latent 변수는 다음과 같다.

\[\begin{equation} z_t^i = \sqrt{\hat{\alpha}_t} (\sqrt{\lambda^i} x^0 + \sqrt{1 - \lambda^i} \Delta x^i) + \sqrt{1 - \hat{\epsilon}_t} \epsilon_t^i \end{equation}\]

따라서 추가된 noise $\epsilon_t^i$도 base noise $b_t^i$와 residual noise $r_t^i$의 두 부분으로 나눈다.

\[\begin{equation} \epsilon_t^i = \sqrt{\lambda^i} b_t^i + \sqrt{1 - \lambda^i} r_t^i, \quad b_t^i, r_t^i \sim \mathcal{N} (0, 1) \end{equation}\]

이를 $z_t^i$ 식에 치환하면 다음과 같다.

\[\begin{equation} z_t^i = \sqrt{\lambda^i} \underbrace{(\sqrt{\hat{\alpha}_t} x^0 + \sqrt{1 - \hat{\alpha}_t} b_t^i)}_{\textrm{diffusion of } x^0} + \sqrt{1 - \lambda^i} \underbrace{(\sqrt{\hat{\alpha}_t} \Delta x^i + \sqrt{1 - \hat{\alpha}_t} r_t^i)}_{\textrm{diffusion of } \Delta x^i} \end{equation}\]

위 식에서 알 수 있듯이 diffusion process는 $x^0$의 diffusion과 $\Delta x^i$의 diffusion의 두 부분으로 분해될 수 있다. 이전 방법에서는 $x^0$가 연속 프레임에서 공유되지만 각 프레임에서 서로 다른 값으로 독립적으로 noise가 발생하므로 denoising의 어려움이 증가할 수 있다. 본 논문은 이 문제를 해결하기 위해 $b_t^i = b_t$가 되도록 $i = 1, 2, \ldots, N$에 대해 $b_t^i$를 공유할 것을 제안한다. 이러한 방식으로 다른 프레임의 $x^0$는 동일한 값으로 noise된다. 그리고 동영상 클립 $x$의 프레임은

\[\begin{equation} z_T \approx \{\sqrt{\lambda^i} b_T + \sqrt{1 - \lambda^i} r_T^i \; \vert \; i = 1, 2, \ldots, N\} \end{equation}\]

으로 인코딩되며, 이는 $b_T$를 통해 상관된 noise 샘플의 시퀀스이다. 이러한 샘플에서 denoising network가 일관된 동영상을 재구성하는 것이 더 쉬울 수 있다.

공유된 $b_t$를 사용하면 noised latent 변수 $z_t^i$는 다음과 같이 표현할 수 있다.

\[\begin{equation} z_t^i = \sqrt{\hat{\alpha}_t} x^i + \sqrt{1 - \hat{\alpha}_t} (\sqrt{\lambda^i} b_t + \sqrt{1 - \lambda^i} r_t^i) \end{equation}\]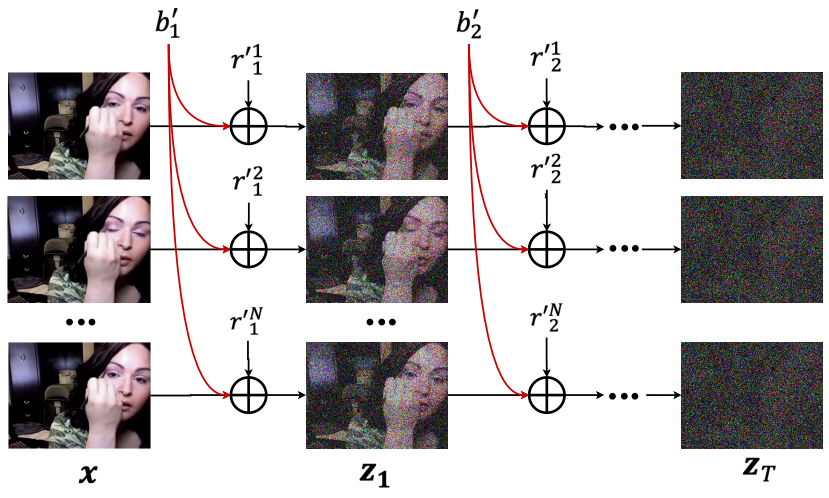

위 그림에서 볼 수 있듯이 이 분해된 형태는 인접한 diffusion step 사이에도 유지된다.

\[\begin{equation} z_t^i = \sqrt{\alpha_t} z_{t-1}^i + \sqrt{1 - \alpha_t} (\sqrt{\lambda^i} b'_t + \sqrt{1 - \lambda^i} {r'}_t^i) \end{equation}\]

여기서 \(b'_t\)와 \(r'_t^i\)는 각각 step $t$에서의 base noise와 residual noise이다. 그리고 \(b'_t\)는 동일한 동영상 클립의 프레임 간에도 공유된다.

3. Using a Pretrained Image DPM

일반적으로 동영상 클립 $x$의 경우 $x^0$와 $\lambda^i$에 대해 무한한 수의 선택이 있다. 그러나 $x^0$가 동영상의 대부분의 정보 (ex. $x^i$와 $x^0$ 사이의 작은 차이만 모델링하면 되는 동영상의 배경 또는 주요 주제)를 담고 있기를 바린다. 경험적으로

\[\begin{equation} x^0 = x^{\lfloor N/2 \rfloor}, \quad \lambda^{\lfloor N/2 \rfloor} = 1 \end{equation}\]

로 설정한다. 여기서 $\lfloor \cdot \rfloor$는 floor 함수이다. 이 경우 $\Delta^{\lfloor N/2 \rfloor} = 0$이고 $z_t^i$는 다음과 같이 단순화할 수 있다.

\[\begin{equation} z_t^i = \begin{cases} \sqrt{\hat{\alpha}_t} x^i + \sqrt{1 - \hat{\alpha}_t} b_t & \quad i = \lfloor N/2 \rfloor \\ \sqrt{\hat{\alpha}_t} x^i + \sqrt{1 - \hat{\alpha}_t} (\sqrt{\lambda^i} b_t + \sqrt{1 - \lambda^i} r_t^i) & \quad i \ne \lfloor N/2 \rfloor \end{cases} \end{equation}\]

위 식은 $x^{\lfloor N/2 \rfloor}$를 $\epsilon$-예측 denoising function $z_\phi^b$에 공급하여 단 한 번의 forward pass로 모든 프레임에 대한 base noise $b_t$를 추정할 수 있는 기회를 제공한다. $z_\phi^b$는 base generator라 부르며, 이미지 diffusion model의 denoising network이다. 이를 통해 DALL-E 2나 Imagen와 같은 사전 학습된 이미지 generator를 base generator로 사용할 수 있다. 이러한 방식으로 사전 학습된 이미지 DPM의 이미지 prior를 활용하여 동영상 데이터 학습을 용이하게 할 수 있다.

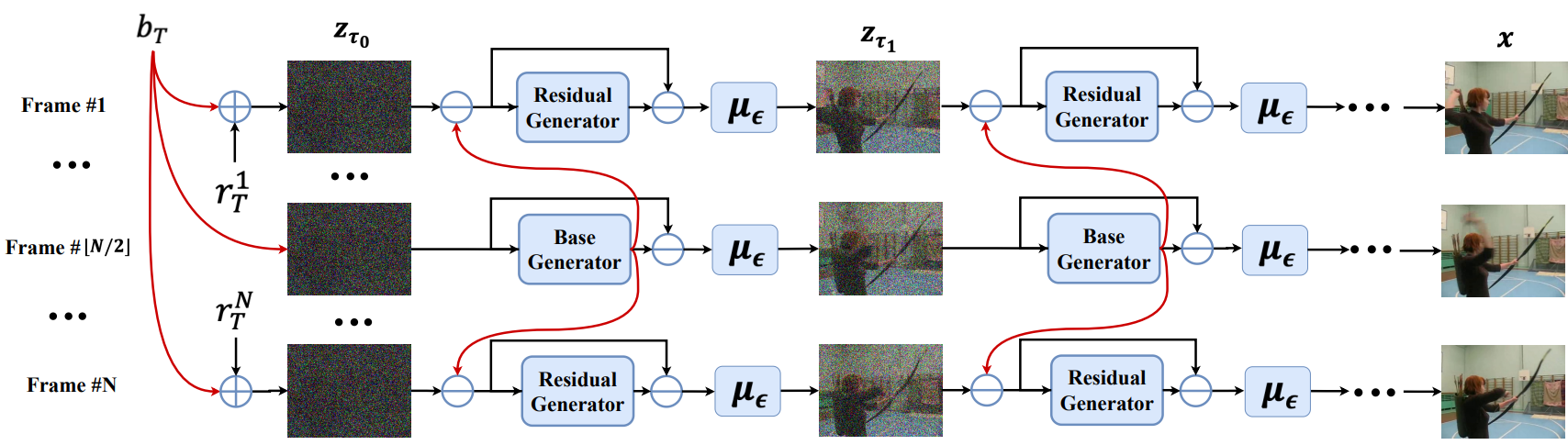
위 그림에서 볼 수 있듯이 각 denoising step에서 먼저 $z_\phi^b (z_t^{\lfloor N/2 \rfloor}, t)$로 base noise를 추정한 다음 모든 프레임에서 제거한다.

\[\begin{equation} z_t^{\prime i} = z_t^i - \sqrt{\lambda^i} \sqrt{1 - \hat{\alpha}_t} z_\phi^b (z_t^{\lfloor N/2 \rfloor}, t), \quad i \ne \lfloor N/2 \rfloor \end{equation}\]

그런 다음 residual generator $z_\psi^r$에 \(z_t^{\prime i}\)를 공급하여 residual noise $r_t^i$를 \(z_\psi^r (z_t^{\prime i}, t, i)\)로 추정한다. Residual generator가 다른 프레임을 구별하기 위해 프레임 번호 $i$로 컨디셔닝된다. $b_t$가 이미 제거되었으므로 \(z_t^{\prime i}\)는 $z_t^i$보다 noise가 적을 것으로 예상된다. 그런 다음 $z_\psi^r$이 나머지 residual noise를 추정하는 것이 더 쉬울 수 있다. Noise $\epsilon_t^i$는 다음과 같이 예측할 수 있다.

\[\begin{equation} \epsilon_t^i = \begin{cases} z_\phi^b (z_t^{\lfloor N/2 \rfloor}, t) & \quad i = \lfloor N/2 \rfloor \\ \sqrt{\lambda^i} z_\phi^b (z_t^{\lfloor N/2 \rfloor}, t) + \sqrt{1 - \lambda^i} z_\psi^r (z_t^{\prime i}, t, i) & \quad i \ne \lfloor N/2 \rfloor \end{cases} \end{equation}\]

그런 다음 DDIM 또는 DDPM의 denoising process를 따라 다음 latent diffusion 변수를 추론하고 샘플 $x^i$를 얻을 때까지 반복할 수 있다.

Base generator $z_\phi^b$는 기본 프레임 $x^{\lfloor N/2 \rfloor}$를 재구성하는 역할을 하는 반면, $z_\psi^r$는 residual $\Delta x^i$를 재구성할 것으로 예상된다. 종종 $x^0$는 풍부한 디테일을 포함하고 학습하기 어렵다. 따라서 사전 학습된 이미지 생성 모델을 사용하여 $x^0$를 재구성하여 이 문제를 크게 완화한다. 또한 각 denoising step에서 $z_\phi^b$는 하나의 프레임만 사용하므로 저렴한 그래프 메모리를 사용하면서 대규모 사전 학습된 모델 (최대 20억 개의 파라미터)을 사용할 수 있다. $x^0$와 비교할 때 residual $\Delta x^i$는 학습하기가 훨씬 쉬울 수 있다. 따라서 residual generator에 상대적으로 작은 네트워크 (5억 개의 파라미터)를 사용할 수 있다. 이러한 방식으로 더 어려운 task, 즉 $x^0$ 학습에 더 많은 파라미터를 집중하여 전체 방법의 효율성을 향상시킨다.

4. Joint Training of Base and Residual Generators

이상적인 경우에는 VideoFusion을 학습하는 동안 사전 학습된 base generator를 고정된 상태로 유지할 수 있다. 그러나 저자들은 사전 학습된 모델을 수정하면 불쾌한 결과를 초래한다는 사실을 실험적으로 발견했다. 저자들은 이것이 이미지 데이터와 동영상 데이터 사이의 도메인 차이 때문이라고 생각한다. 따라서 작은 learning rate로 동영상 데이터에서 base generator $z_\theta^b$를 동시에 fine-tuning하는 것이 도움이 된다. 최종 loss function을 다음과 같이 정의한다.

\[\begin{equation} \mathcal{L}_t = \begin{cases} \| \epsilon_t^i - z_\phi^b (z_t^{\lfloor N/2 \rfloor}, t) \|^2 & \quad i = \lfloor N/2 \rfloor \\ \| \epsilon_t^i - \sqrt{\lambda^i} [z_\theta^b (z_t^{\lfloor N/2 \rfloor}, t)]_\textrm{sg} - \sqrt{1 - \lambda^i} z_\psi^b (z_t^{\prime i}, t, i) \|^2 & \quad i \ne \lfloor N/2 \rfloor \end{cases} \end{equation}\]

여기서 \([\cdot]_\textrm{sg}\)는 stop-gradient 연산이며, 이는 $i \ne \lfloor N/2 \rfloor$일 때 기울기가 $z_\theta^b$로 전파되지 않음을 의미한다. 사전 학습된 모델이 기본 프레임의 loss에 의해서만 fine-tuning되기를 바란다. 이는 학습 초기에 \(z_\psi^r (z_t^{\prime i}, t)\)의 추정 결과에 noise가 있어 사전 학습된 모델을 파괴할 수 있기 때문이다.

5. Discussions

일부 GAN 기반 방법에서 동영상은 두 개의 연결된 noise, 즉 콘텐츠 코드와 모션 코드에서 생성되며 콘텐츠 코드는 프레임 간에 공유된다. 이러한 방법은 다양한 콘텐츠 코드와 모션 코드를 샘플링하여 동영상 콘텐츠와 모션을 제어하는 능력을 보여준다. 이러한 아이디어를 DPM 기반의 방법에 직접적으로 적용하기는 어려운데, 이는 DPM에서 noised latent 변수가 생성된 영상과 동일한 형태를 가져야 하기 때문이다.

제안된 VideoFusion에서는 추가된 noise를 base noise와 residual noise의 가중 합으로 표현하여 분해하고 latent 동영상 공간도 분해할 수 있다. DDIM 샘플링 알고리즘에 따르면 공유 기본 프레임 $x^{\lfloor N/2 \rfloor}$는 base noise $b_T$에만 의존한다. 이를 통해 $b_T$를 통해 동영상 콘텐츠를 제어할 수 있다. $b_T$를 고정하여 콘텐츠는 같지만 모션이 다른 동영상을 생성하여 더 긴 일관된 시퀀스를 생성하는 데 도움이 된다.

그러나 VideoFusion이 residual noise를 동영상 모션과 관련시키는 방법을 자동으로 학습하는 것은 어려울 수 있다. Residual noise generator가 base noise 또는 residual noise를 가중 합과 구별하기 어렵기 때문이다. 반면에 VideoFusion에 mini-batch에서 동일한 모션이 있는 동영상도 동일한 residual noise를 공유한다는 명시적인 학습 guidance를 VideoFusion에 제공하면 VideoFusion이 residual noise를 동영상 모션과 관련시키는 방법을 학습할 수도 있다.

Experiments

• 데이터셋: UCF101, Sky Time-lapse, TaiChi-HD, WebVid-10M
• 학습
  • LAION-5B에서 사전 학습된 DALL-E 2의 디코더를 base generator로 사용
  • 랜덤하게 초기화된 2D U모양 denoising network를 residual generator로 사용
  • 두 generator 모두 동영상 샘플의 중앙 이미지에서 CLIP의 visual encoder에 의해 추출된 이미지 임베딩을 조건으로 함
  • Prior도 latent 임베딩을 생성하도록 학습됨
  • 조건부 동영상 생성의 경우 prior는 동영상 캡션 또는 클래스를 조건으로 함
  • Unconditional 생성의 경우 prior의 조건은 빈 텍스트
  • 처음에 64$\times$64 해상도의 16프레임 동영상 클립으로 학습된 다음 DPM 기반 SR 모델을 사용하여 더 높은 해상도로 super-resolution
  • $\lambda^i = 0.5, \forall i \ne 8$, $\lambda^8 = 0.5$로 설정

1. Quantitative Results

다음은 UCF101에서 정량적으로 비교힌 표이다.

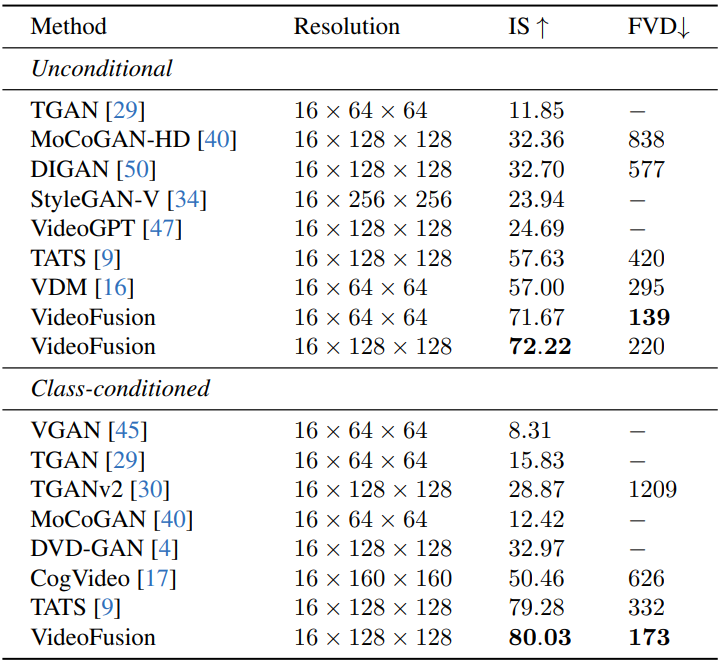
다음은 Sky Time-lapse에서 정량적으로 비교힌 표이다.

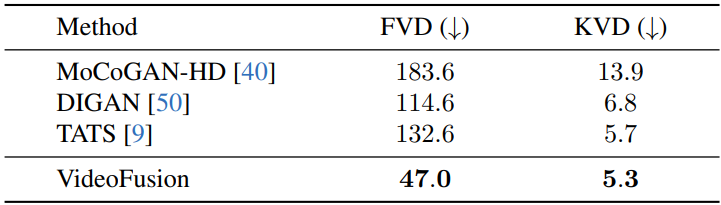
다음은 TaiChi-HD에서 정량적으로 비교힌 표이다.

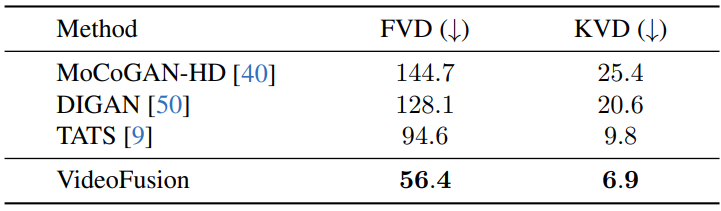
2. Qualitative Results

다음은 (a) UCF101, (b) Sky Time-lapse, (c) TaiChi-HD에서의 시각적 비교 결과이다.

다음은 WebVid-10M에서 학습된 VideoFusion의 text-to-video 생성 결과이다.

3. Efficiency Comparison

다음은 VideoFusion의 base generator를 기반으로 VDM을 다시 구현하고 (VDM*로 표시) 효율성을 비교한 표이다.

4. Ablation study

다음은 여러 $\lambda^i$에 대한 unconditional 생성 결과이다. (UCF101)

다음은 사전 학습에 대한 unconditional 생성 결과이다. (UCF101)

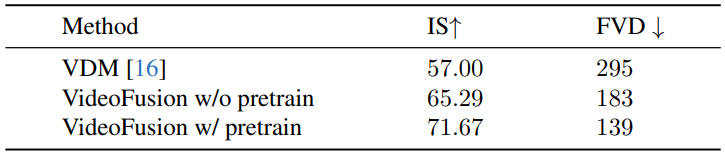
다음은 공동 학습에 대한 unconditional 생성 결과이다. (UCF101)

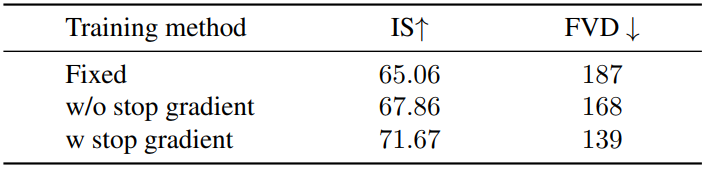
5. Generating Long Sequences

다음은 UCF101 (위), Sky Time-lapse (중간), TaiChi-HD (아래)에서 512프레임으로 생성된 동영상이다.

Limitations

1. 연속 프레임 간에 base noise를 공유하면 생성된 동영상의 움직임을 제한할 수도 있다.
2. 동영상마다 프레임 간의 차이가 다르기 때문에 모든 동영상에 적합한 $\lambda^i$를 찾기가 어렵다.
3. 긴 텍스트에서 동영상을 생성하는 경우 prior에 캡션의 긴 시간 정보를 latent 임베딩으로 인코딩하는 것이 어려울 수 있다.