[논문리뷰] Video Diffusion Models

arXiv 2022. [Paper] [Page]
Jonathan Ho, Tim Salimans, Alexey Gritsenko, William Chan, Mohammad Norouzi, David J. Fleet
Google Research, Brain Team
7 Apr 2022

Introduction

Diffusion model은 최근 이미지 생성과 오디오 생성에서 고품질 결과를 생성하고 있으며 새로운 데이터 modality에서 diffusion model 검증하는 데 상당한 관심이 있다. 본 논문에서는 unconditional 및 conditional 설정 모두에 대해 diffusion model을 사용하여 동영상 생성에 대한 첫 번째 결과를 제시한다.

딥 러닝 가속기의 메모리 제약 내에서 동영상 데이터를 수용하기 위해 간단한 아키텍처 변경 외에 거의 수정하지 않고 본질적으로 Gaussian diffusion model의 표준 공식을 사용하여 고품질 동영상을 생성할 수 있음을 보여준다. 3D U-Net diffusion model 아키텍처를 사용하여 고정된 수의 동영상 프레임을 생성하는 모델을 학습하고 새로운 조건부 생성 방법을 사용하여 이 모델을 autoregressive하게 적용하여 더 긴 동영상을 생성할 수 있다. 또한 동영상 및 이미지 모델링 목적 함수에 대한 공동 학습의 이점을 보여준다. 본 논문은 state-of-the-art 샘플 품질 점수를 달성하는 동영상 예측 및 unconditional 동영상 생성에 대한 방법을 테스트하고 텍스트 조건부 동영상 생성에 대한 유망한 결과도 처음으로 보여준다.

Background

연속 시간에서의 diffusion model은 데이터 $x \sim p(x)$에서 시작하는 forward process $q(z \vert x)$를 따르는 latent $z = {z_t \vert t \in [0, 1]}$$를 갖는 생성 모델이다. Forward process는 Markovian 구조를 만족하는 Gaussian process이다.

\[\begin{equation} q(z_t \vert x) = \mathcal{N}(z_t; \alpha_t x, \sigma_t^2 I), \quad q(z_t \vert z_s) = \mathcal{N}(z_t; (\alpha_t / \alpha_s) z_s, \sigma_{t \vert s}^2 I) \\ \textrm{where} \; \quad 0 \le s < t \le 1, \quad \sigma_{t \vert s}^2 = (1 - e^{\lambda_t - \lambda_s}) \sigma_t^2, \quad \lambda_t = \log [\alpha_t^2 / \sigma_t^2] \end{equation}\]

Training

생성을 위하여 forward process를 역으로 학습하는 것은 $z_t \sim q(z_t \vert x)$를 모든 $t$에 대한 추정치 \(\hat{x}_\theta (z_t, \lambda_t) \approx x\)로 noise를 제거하는 학습으로 축소될 수 있다 (표기법을 단순화하기 위해 $λ_t$에 대한 의존성을 삭제). 가중 MSE loss를 사용하여 denoising model $\hat{x}_\theta$를 학습시킨다.

\[\begin{equation} \mathbb{E}_{\epsilon, t} [w(\lambda_t) \| \hat{x}_\theta (z_t) - x \|_2^2] \end{equation}\]

이러한 축소는 diffusion model에서 데이터 log-likelihood에 대한 weighted VLB을 최적화하거나 denoising score matching의 형태로 정당화될 수 있다. 실제로

\[\begin{equation} \hat{x}_\theta (z_t) = \frac{z_t − \sigma_t \epsilon_\theta (z_t)}{\alpha_t} \end{equation}\]

로 정의되는 $\epsilon$-prediction parameterization을 사용하고 cosine schedule에 따라 샘플링된 $t$를 사용하여 $\epsilon$ space에서 MSE를 사용하여 $\epsilon_\theta$를 학습시킨다. 이는 스케일링된 score 추정치

\[\begin{equation} \epsilon_\theta (z_t) \approx − \sigma_t \nabla_{z_t} \log p(z_t) \end{equation}\]

를 학습하기 위한 특정 가중치 $w(\lambda_t)$에 해당하며, 여기서 $p(z_t)$는 $x \sim p(x)$에서 $z_t$의 실제 밀도이다. 또한 특정 모델의 경우 $v$-prediction parameterization을 사용하여 학습시킨다.

Sampling

본 논문에서는 다양한 diffusion model sampler를 사용한다. 하나는 reverse process 엔트로피의 하한 및 상한에서 유도된 샘플링 분산을 사용하는 이산 시간 ancestral sampler이다. Forward process는 다음과 같이 역순으로 설명할 수 있다.

\[\begin{equation} q(z_s \vert z_t, x) = \mathcal{N} (z_s; \tilde{\mu}_{s \vert t} (z_t, x), \tilde{\sigma}_{s \vert t}^2 I) \\ \textrm{where} \quad \tilde{\mu}_{s \vert t} (z_t, x) = e^{\lambda_t - \lambda_s} (\alpha_s / \alpha_t) z_t + (1 - e^{\lambda_t - \lambda_s} \alpha_s) x \\ \textrm{and} \quad \tilde{\sigma}_{s \vert t}^2 = (1 - e^{\lambda_t - \lambda_s}) \sigma_s^2 \end{equation}\]

$z_1 \sim \mathcal{N}(0, 1)$에서 시작하여 ancestral sampler는 다음 규칙을 따른다.

\[\begin{equation} z_s = \tilde{\mu}_{s \vert t} (z_t, \hat{x}_\theta (z_t)) + \sqrt{(\tilde{\sigma}_{s \vert t}^2)^{1 - \gamma}(\tilde{\sigma}_{t \vert s}^2)^\gamma} \epsilon \end{equation}\]

$\gamma$는 sampler의 stochasity를 조절하는 hyperparameter이다. $\epsilon$은 Gaussian noise이다.

또다른 sampler는 predictor-corrector sampler로, 조건부 생성을 위한 본 논문의 새로운 방법이 특히 효과적이라고 한다. 이 sampler의 본 논문의 버전은 ancestral sampler step과

\[\begin{equation} z_s \leftarrow z_s - \frac{1}{2} \delta \sigma_s \epsilon_\theta (z_s) + \sqrt{\delta} \sigma_s \epsilon' \end{equation}\]

형식의 Langevin correction step 사이를 번갈아 가며 나타낸다.

여기서 $\delta$는 step size이며 본 논문에서는 0.1로 고정된다. $\epsilon’$은 또다른 Gaussian noise이다. Langevin step의 목적은 각 $z_s$의 주변 분포가 $x \sim p(x)$에서 시작한 forward process의 실제 주변 분포와 일치하도록 만드는 것이다.

조건부 생성 설정에서는 데이터 $x$가 컨디셔닝 신호 $c$와 함께 사용된다. $p(x \vert c)$에 맞게 diffusion model을 학습시키기 위해 필요한 유일한 수정은 모델에 $c$를 \(\tilde{x}_\theta (z_t, c)\)로 제공하는 것이다. Clssifier-free guidance를 사용하여 이 설정에서 샘플 품질을 개선할 수 있다. 이 방법은 다음을 통해 구성된 조정된 모델 예측 \(\tilde{\epsilon}_\theta\)를 사용하여 샘플링한다.

\[\begin{equation} \tilde{\epsilon}_\theta (z_t, c) = (1 + w) \epsilon_\theta (z_t, c) - w \epsilon_\theta (z_t) \end{equation}\]

여기서 $w$는 guidance 강도이다. $w > 0$의 경우 이 조정은 $c$에 대한 컨디셔닝 효과를 과도하게 강조하는 효과가 있으며, 일반 조건부 모델의 샘플링에 비해 다양성은 낮지만 품질은 더 높은 샘플을 생성하는 경향이 있다.

Video diffusion models

Diffusion model을 사용한 동영상 생성에 대한 접근 방식은 표준 diffusion model 형식을 동영상 데이터에 적합한 신경망 아키텍처와 함께 사용하는 것이다. 각 모델은 고정된 공간 해상도에서 고정된 수의 프레임을 공동으로 모델링하도록 학습되었다. 샘플링을 더 긴 프레임 시퀀스 또는 더 높은 공간 해상도로 확장하기 위해 컨디셔닝 기술을 사용하여 모델의 용도를 변경한다.

이미지 모델링에 대한 이전 연구에서 이미지 diffusion model의 \(\hat{x}_\theta\)에 대한 표준 아키텍처는 U-Net이다. 네트워크는 예를 들어 Wide ResNet 스타일의 2D convolution residual block layer로 구성되며 이러한 각 convolution block 뒤에는 spatial attention block이 있다. $c$와 $\lambda_t$와 같은 컨디셔닝 정보는 각 residual block에 추가된 임베딩 벡터의 형태로 네트워크에 제공된다. 여러 MLP layer를 사용하여 이러한 임베딩 벡터를 처리하는 것이 도움이 된다.

본 논문은 공간과 시간에 걸쳐 분해되는 특정 유형의 3D U-Net을 사용하여 고정된 수의 프레임 블록으로 제공되는 이 이미지 diffusion model 아키텍처를 동영상 데이터로 확장할 것을 제안한다. 먼저 각 2D convolution을 space-only 3D convolution으로 변경하여 이미지 모델 아키텍처를 수정한다. 예를 들어 각 3$\times$3 convolution을 1$\times$3$\times$3 convolution으로 변경한다. 각 spatial attention block의 attention은 공간에 대한 attention으로 남아 있다. 즉, 첫 번째 축은 배치 축으로 처리된다.

둘째, 각 spatial attention block 뒤에 첫 번째 축에 대한 attention을 수행하고 공간 축을 배치 축으로 취급하는 temporal attention block을 삽입한다. 네트워크가 동영상 시간의 절대적인 개념을 필요로 하지 않는 방식으로 프레임의 순서를 구별할 수 있도록 각 temporal attention block에서 relative position embedding을 사용한다. 아래 그림은 모델 아키텍처를 시각화한 것이다.

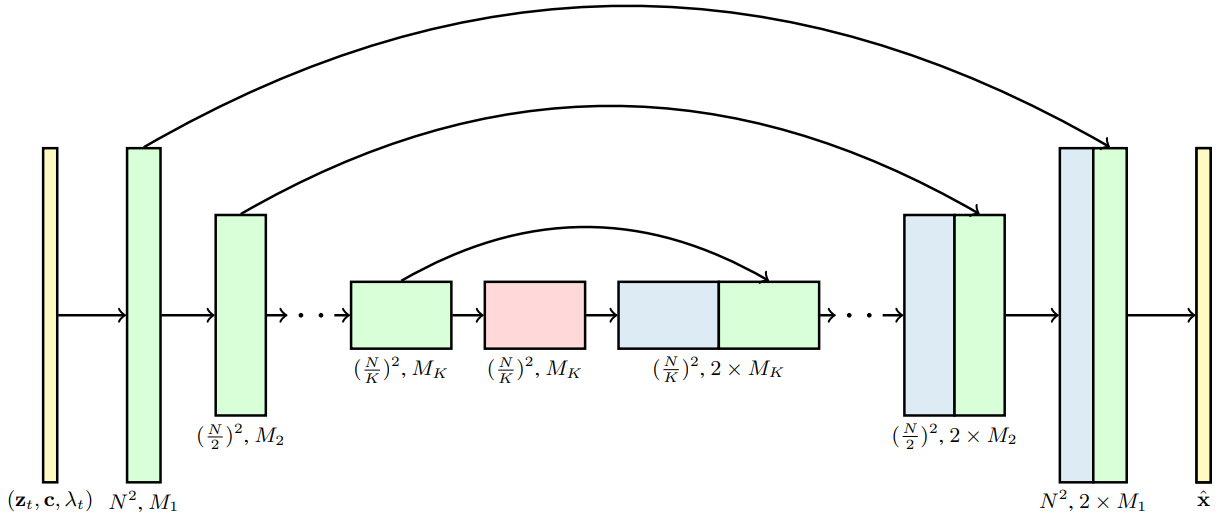
분해된 시공간적 attention의 사용은 계산 효율성을 위해 video transformer에서 좋은 선택인 것으로 알려져 있다. 동영상 생성 설정을 위한 분해된 시공간적 아키텍처의 장점은 각 temporal attention block 내에서 attention 연산을 제거함으로써 동영상이 아닌 독립적인 이미지에서 실행되도록 모델을 마스킹하는 것이 특히 간단하다는 것이다. 각 동영상 timestep에서 각 key와 query 벡터가 정확히 일치하도록 attention matrix를 고정한다. 그렇게 하면 동영상 생성과 이미지 생성 모두에서 모델을 공동으로 학습할 수 있다는 것이다. 저자들은 실험을 통해 이 공동 학습이 샘플 품질에 중요하다는 것을 발견했다.

1. Reconstruction-guided sampling for improved conditional generation

모델링하려는 동영상은 일반적으로 초당 최소 24프레임의 프레임 속도에서 수백에서 수천 개의 프레임으로 구성된다. 모델 학습의 계산 요구 사항을 관리하기 위해 한 번에 16개 프레임의 작은 부분 집합에 대해서만 학습한다. 그러나 테스트 시에는 샘플을 확장하여 더 긴 동영상을 생성할 수 있다.

예를 들어 먼저 16개 프레임으로 구성된 동영상 $x^a \sim p_\theta (x)$를 생성한 다음 두 번째 샘플 $x^b \sim p_\theta (x^b \vert x^a)$로 확장할 수 있다. $x^b$가 $x^a$ 이후의 프레임으로 구성되어 있으면 샘플링된 동영상을 임의의 길이로 autoregressive하게 확장할 수 있다. 또는 $x^a$를 선택하여 더 낮은 프레임 속도의 동영상을 표시한 다음 $x^b$를 $x^a$의 프레임 사이에 있는 프레임으로 정의할 수 있다. 이를 통해 공간적 upsampling을 통해 고해상도 이미지를 생성하는 방법과 유사하게 동영상을 시간적으로 upsampling할 수 있다.

두 접근 방식 모두 조건부 모델 $p_\theta (x^b \vert x^a)$에서 샘플링해야 한다. 이 조건부 모델은 명시적으로 학습될 수 있지만, unconditional model $p_\theta (x)$에서 대략적으로 파생될 수도 있으며, 이는 별도로 학습된 모델이 필요하지 않다는 이점이 있다.

예를 들어 Score-based generative modeling through stochastic differential equations 논문은 공동으로 학습된 diffusion model $p_\theta (x = [x^a, x^b])$에서 조건부 샘플링을 위한 일반적인 방법을 제시하였다. $p_\theta (x^b \vert x^a)$에서 샘플링하는 접근 방식에서 $z_s^b$를 업데이트하기 위한 샘플링 절차는 $p_\theta (z_s \vert z_t), z_s = [z_s^a, z_s^b]$이지만 $z_s^a$에 대한 샘플은 각 iteration에서 forward process $q (z_s^a \vert x^a)$의 정확한 샘플로 대체된다. 그러면 샘플 $z_s^a$는 구성에 의한 올바른 주변 분포를 가지며 샘플 $z_s^b$는 denoising model \(\hat{x}_\theta ([z_t^a, z_t^b])\)에 대한 영향을 통해 $z_s^a$를 따른다. 유사하게 $q(z_s^a \vert x^a, z_t^a)$에서 $z_s^a$를 샘플링할 수 있으며, 이는 올바른 조건부 분포와 주변 분포를 따른다. 이 두 가지 접근 방식을 diffusion model에서 조건부 샘플링을 위한 replacement 방법이라 부른다.

저자들이 조건부 샘플링에 대한 replacement 방법을 시도했을 때 동영상 모델에 대해 제대로 작동하지 않는 것으로 나타났다. 샘플 $x^b$는 단독으로 보기에 좋았지만 $x^a$와 일관성이 없었다. 이는 이 replacement 샘플링 방식의 근본적인 문제에 기인한다. 즉, latent $z_s^b$는 \(\hat{x}_\theta^b (z_t) \approx \mathbb{E}_q [x^b \vert z_t]\)의해 제공되는 방향으로 업데이트되는 반면, 대신 필요한 것은 $\mathbb{E}_q [x^b \vert z_t, x^a]$이다. 이것을 데이터 분포의 score로 쓰면

\[\begin{equation} \mathbb{E}_q [x^b \vert z_t, x^a] = \mathbb{E}[x^b \vert z_t] + \frac{\sigma_t^2}{\alpha_t} \nabla_{z_t^b} \log q(x^a \vert z_t) \end{equation}\]

가 된다. 여기서 두 번째 항은 replacement 방법에서 누락되었다. 완벽한 denoising model을 가정하면 이 누락된 항을 연결하면 조건부 샘플링이 정확해진다. 그러나 $q(x^a \vert z_t)$는 closed form으로 사용할 수 없기 때문에 대신

\[\begin{equation} q(x^a \vert z_t) \approx \mathcal{N}(\hat{x}_\theta^a (z_t), (\sigma_t^2 / \alpha_t^2) I) \end{equation}\]

형식의 Gaussian을 사용하여 근사한다. 여기서 \(\hat{x}_\theta^a (z_t)\)는 denoising model에서 제공하는 컨디셔닝 데이터 $x^a$의 재구성이다. 완벽한 모델을 가정하면 이 근사값은 $t$가 0에 가까워짐에 따라 정확해지고 경험적으로 더 큰 $t$에도 적합하다는 것을 알 수 있다. 이 근사값을 사용하고 가중 계수 $w_r$을 추가하면 조건부 샘플링에 제안된 방법은 다음과 같이 정의되는 조정된 denoising model \(\tilde{x}_\theta^b\)를 사용한 replacement 방법의 변형이다.

\[\begin{equation} \tilde{x}_\theta^b (z_t) = \hat{x}_\theta^b (z_t) - \frac{w_r \alpha_t}{2} \nabla_{z_t^b} \| x^a - \hat{x}_\theta^a (z_t) \|_2^2 \end{equation}\]

이 식의 추가 기울기 항은 모델의 컨디셔닝 데이터 재구성을 기반으로 한 guidance의 한 형태로 해석될 수 있으므로 이 방법을 reconstruction-guided sampling 또는 단순히 reconstruction guidance라고 한다. 다른 형태의 guidance와 마찬가지로 더 큰 가중치 계수($w_r > 1$)를 선택하면 샘플 품질이 향상되는 경향이 있다.

Reconstruction guidance은 모델 예측의 downsampling된 버전에 MSE loss가 부과되고 이 downsampling을 통해 역전파가 수행되는 spatial interpolation (또는 super-resolution)의 경우에도 확장된다. 이 설정에서 저해상도 모델에서 생성될 수 있는 저해상도 ground-truth 동영상 $x^a$ (ex. 64$\times$64)를 가지고 있으며 고해상도 모델 \(\hat{x}_\theta\)를 사용하여 고해상도 동영상(ex. 128$\times$128)으로 upsampling하려고 한다. 이를 고해상도 모델을 다음과 같이 조정한다.

\[\begin{equation} \tilde{x}_\theta (z_t) = \hat{x}_\theta (z_t) - \frac{w_r \alpha_t}{2} \nabla_{z_t} \| x^a - \hat{x}_\theta^a (z_t) \|_2^2 \end{equation}\]

여기서 \(\hat{x}_\theta^a (z_t)\)는 bilinear interpolation과 같은 미분 가능한 downsampling 알고리즘을 사용하여 모델의 고해상도 출력을 downsampling하여 얻은 $z_t$의 저해상도 동영상에 대한 모델의 재구성이다. 동일한 reconstruction guidance 방법을 사용하여 고해상도에서 샘플을 autoregressive하게 확장하면서 저해상도 동영상에서 동시에 컨디셔닝할 수도 있다.

아래 그림은 9$\times$128$\times$128 diffusion model을 사용하여 frameskip 4에서의 16$\times$64$\times$64 저해상도 샘플을 frameskip 1에서의 64$\times$128$\times$128 샘플로 확장하기 위한 이 접근법의 샘플들을 보여준다.

Experiments

1. Unconditional video modeling

다음은 UCF101에서의 unconditional 동영상 모델링 결과이다.

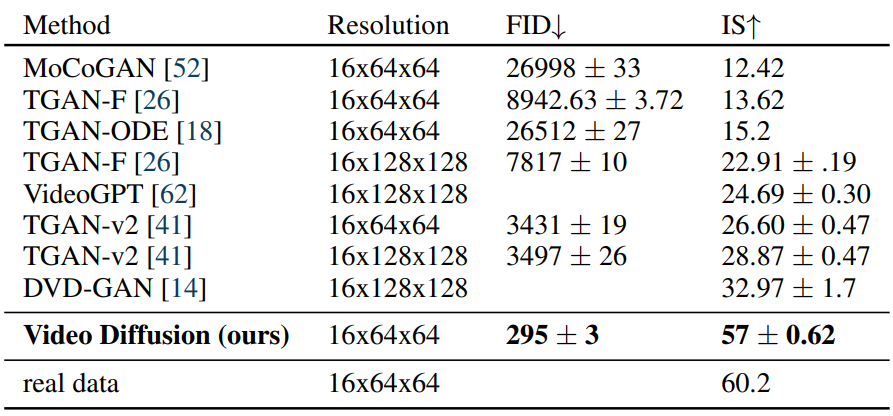
2. Video prediction

다음은 BAIR Robot Pushing에서의 동영상 예측 결과이다.

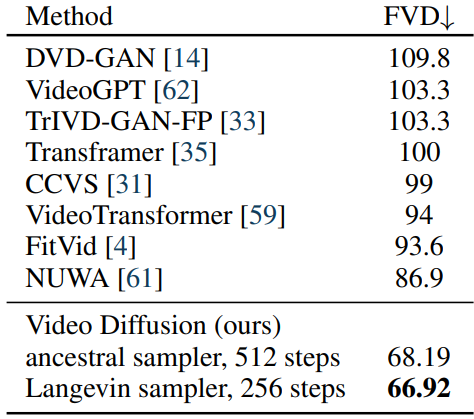
다음은 Kinetics-600에서의 동영상 예측 결과이다.

3. Text-conditioned video generation

Joint training on video and image modeling

다음은 동영상당 0, 4, 8개의 독립적인 추가 이미지 프레임들을 사용하여 학습한 결과이다.

Effect of classifier-free guidance

다음은 text-to-video 생성에서 classifier-free guidance의 효과를 보여주는 표이다.

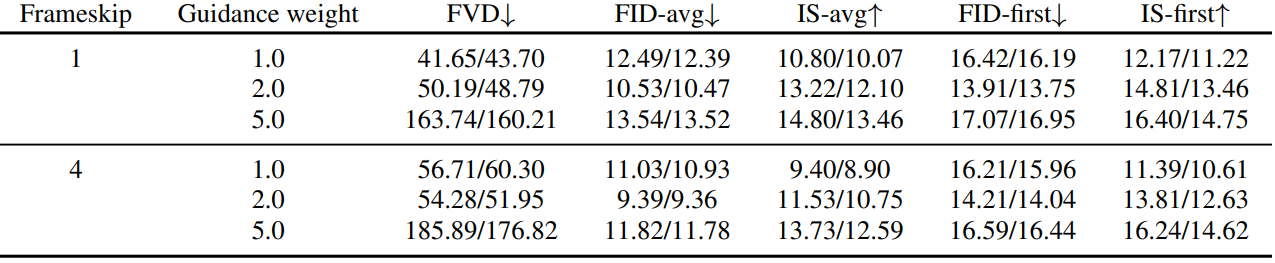
다음은 텍스트 조건부 동영상 모델에서 classifier-free guidance의 효과를 보여주는 그림이다. 왼쪽은 guide되지 않은 샘플들이고 오른쪽은 classifier-free guidance를 사용하여 guide한 샘플들이다.

Autoregressive video extension for longer sequences

다음은 16$ 프레임 모델을 autoregressive하게 확장하여 64 프레임 동영상을 생성할 때 reconstruction guidance 방법과 replacement 방법을 비교한 표이다.

다음은 replacement 방법(왼쪽)과 reconstruction guidance 방법(오른쪽)으로 16 프레임 모델을 64 프레임으로 확장한 예시이다.

replacement 방법은 reconstruction guidance 방법과 달리 시간적 일관성이 부족하다.