[논문리뷰] VGGT: Visual Geometry Grounded Transformer

CVPR 2025 (Best Paper). [Paper] [Page] [Github]
Jianyuan Wang, Minghao Chen, Nikita Karaev, Andrea Vedaldi, Christian Rupprecht, David Novotny
Visual Geometry Group, University of Oxford | Meta AI
14 Mar 2025

Introduction

최근 DUSt3R와 MASt3R는 3D task를 신경망으로 직접 해결하였지만, 한 번에 두 개의 이미지만 처리할 수 있으며, 더 많은 이미지를 재구성하기 위해 후처리에 의존하여 쌍으로 재구성한 내용을 융합한다.

본 논문에서는 한 개에서 심지어 수백 개의 장면 입력 뷰를 사용하여 3D 재구성을 수행하는 feed-forward 신경망인 Visual Geometry Grounded Transformer (VGGT)를 도입하였으며, 이를 통해 후처리 과정으로 3D geometry를 최적화할 필요성을 없애기 위한 한 걸음 더 나아갔다. VGGT는 카메라 파라미터, depth map, point map, 3D point track을 포함한 전체 3D 속성 집합을 예측하며, 단 한 번의 forward pass로 몇 초 만에 이 모든 과정을 완료한다. 놀랍게도, 추가 처리 없이도 최적화 기반 대안보다 성능이 훨씬 뛰어나다.

또한 3D 재구성을 위해 특별한 네트워크를 설계할 필요가 없음을 보여주었다. 대신 VGGT는 특정 3D 또는 기타 inductive bias가 없는 상당히 표준적인 transformer를 기반으로 하지만 3D 주석이 있는 많은 수의 공개적으로 사용 가능한 데이터셋에 대해 학습되었다. 따라서 VGGT는 GPT, CLIP, DINO, Stable Diffusion과 같은 대형 모델과 동일한 틀에서 구축되었다. 이러한 모델들은 새로운 특정 task를 해결하도록 fine-tuning할 수 있는 다재다능한 backbone이다. 마찬가지로 VGGT에서 계산된 feature가 동적 동영상의 point tracking, novel view synthesis (NVS)와 같은 다운스트림 task를 크게 향상시킬 수 있다.

최근 대규모 3D 신경망 모델들은 monocular depth estimation이나 NVS와 같은 하나의 3D task에만 초점을 맞춘다. 이와 대조적으로 VGGT는 공유 backbone을 사용하여 관심있는 모든 3D 값들을 함께 예측한다. 이러한 상호 연관된 3D 속성을 예측하는 학습이 잠재적 중복성에도 불구하고 전반적인 정확도를 향상시켰다. 동시에 inference 과정에서 개별적으로 예측된 ​​깊이 및 카메라 파라미터로부터 point map을 도출할 수 있으며, 전용 point map head를 직접 사용하는 것보다 더 높은 정확도를 얻을 수 있다.

Method

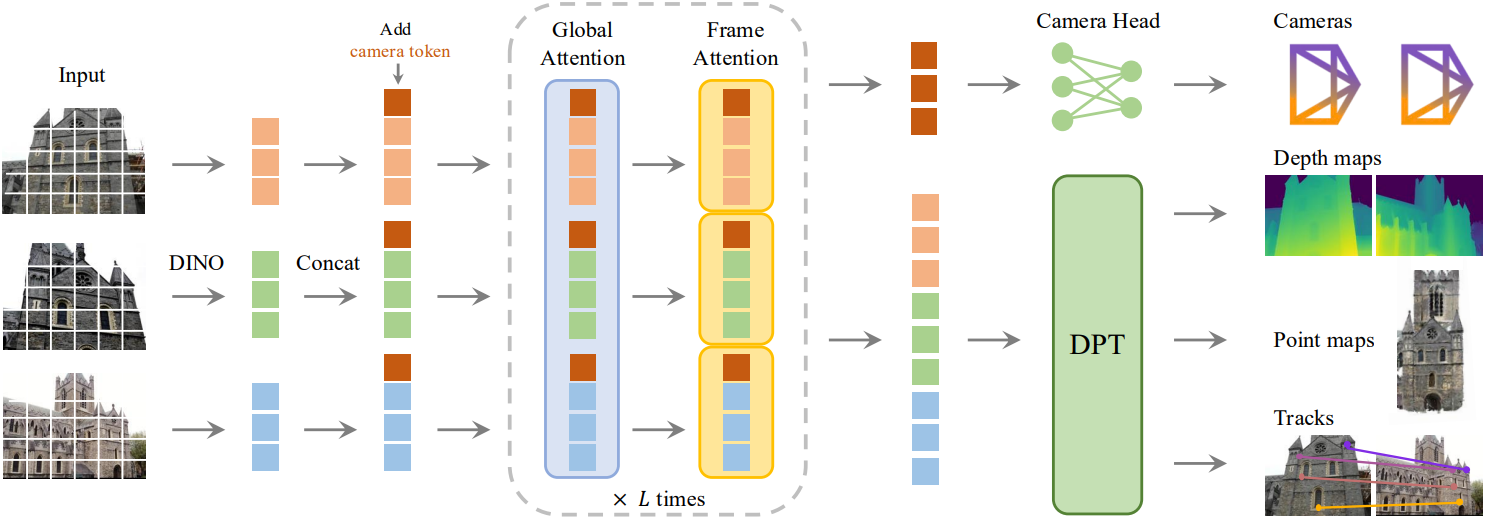
1. Problem definition and notation

입력은 동일한 3D 장면을 관찰하는 $N$개의 RGB 이미지 $I_i \in \mathbb{R}^{3 \times H \times W}$로 구성된 시퀀스 \((I_i)_{i=1}^N\)이다. VGGT의 transformer는 이 시퀀스를 프레임당 하나씩 해당하는 3D 주석 집합으로 매핑하는 함수이다.

\[\begin{equation} f((I_i)_{i=1}^N) = (\textbf{g}_i, D_i, P_i, T_i)_{i=1}^N \end{equation}\]

따라서 transformer는 각 이미지 $I_i$를 카메라 파라미터 \(\textbf{g}_i \in \mathbb{R}^9\) (intrinsic, extrinsic), depth map $D_i \in \mathbb{R}^{H \times W}$, point map $P_i \in \mathbb{R}^{3 \times H \times W}$, 그리고 point tracking을 위한 tracking feature $T_i \in \mathbb{R}^{C \times H \times W}$에 매핑한다.

카메라 파라미터 \(\textbf{g}_i\)의 경우, VGGSfM의 parametrization을 사용하여 rotation quaternio \(\textbf{q} \in \mathbb{R}^4\), translation vector \(\textbf{t} \in \mathbb{R}^3\), FOV \(\textbf{f} \in \mathbb{R}^2\)를 concat한 \(\textbf{g} = [\textbf{q}, \textbf{t}, \textbf{f}]\)를 사용한다. 카메라의 principal point가 이미지 중심에 있다고 가정한다.

Depth map $D_i$는 각 픽셀 위치 $\textbf{y}$를 $i$번째 카메라에서 관찰한 해당 깊이 값 \(D_i (\textbf{y}) \in \mathbb{R}^{+}\)와 연결한다. 마찬가지로, point map $P_i$는 각 픽셀을 해당 3D 장면 포인트 \(P_i (\textbf{y}) \in \mathbb{R}^3\)와 연결하며, DUSt3R와 마찬가지로 첫 번째 카메라 \(\textbf{g}_1\)의 좌표계에서 정의된다.

Keypoint tracking의 경우 track-any-point 방식을 따른다. 즉, 쿼리 이미지 $I_q$에 고정된 쿼리 이미지 포인트 \(\textbf{y}_q\)가 주어지면, 네트워크는 모든 이미지 Ii에 있는 해당 2D 포인트 \(\textbf{y}_i \in \mathbb{R}^2\)로 구성된 track \(\mathcal{T}^\ast (\textbf{y}_q) = (\textbf{y}_i)_{i=1}^N\)을 출력한다.

Transformer $f$는 track을 직접 출력하지 않고 tracking에 사용되는 feature $T_i \in \mathbb{R}^{C \times H \times W}$를 출력한다. Tracking은 별도의 모듈에 위임되며, 이 모듈은 transformer $f$가 출력한 쿼리 포인트 \(\textbf{y}_q\)와 dense tracking feature $T_i$를 수집한 후 track을 계산한다.

\[\begin{equation} \mathcal{T} ((\textbf{y}_j)_{j=1}^M, (T_i)_{i=1}^N) = ((\hat{\textbf{y}}_{j,i})_{i=1}^N)_{j=1}^M \end{equation}\]

두 네트워크 $f$와 $\mathcal{T}$는 end-to-end로 공동 학습된다.

예측 순서

입력 시퀀스에서 이미지의 순서는 임의적이지만, 첫 번째 이미지가 레퍼런스 프레임으로 선택된다. 네트워크 아키텍처는 첫 번째 프레임을 제외한 모든 프레임에 대해 순열 동치성을 갖도록 설계되었다.

Over-complete Prediction

주목할 점은 VGGT로 예측된 ​​모든 값이 독립적인 것은 아니라는 것이다. 예를 들어, 카메라 파라미터 $\textbf{g}$는 point map $P$로부터 추론될 수 있다. 또한 depth map은 point map과 카메라 파라미터로부터 추론될 수 있다.

그러나, VGGT가 학습 과정에서 모든 값을 명시적으로 예측하도록 하면, closed-form 관계로 연결되어 있더라도 상당한 성능 향상을 얻을 수 있다. 한편, inference 과정에서는 독립적으로 추정된 depth map과 카메라 파라미터를 결합하는 것이 point map branch를 직접 사용하는 것보다 더 정확한 3D 포인트를 생성하는 것으로 나타났다.

2. Feature Backbone

저자들은 3D 딥러닝 분야의 최근 연구 결과를 바탕으로, 3D inductive bias를 최소화하기 위해 모델 $f$를 큰 transformer로 구현했으며, 모델이 풍부한 양의 3D 주석 데이터를 통해 학습할 수 있도록 했다. 이를 위해 각 입력 이미지 $I$는 DINO를 통해 $K$개 토큰의 집합 $\textrm{t}^I \in \mathbb{R}^{K \times C}$로 patchify된다. 모든 프레임의 이미지 토큰 세트 \(\textrm{t}^I = \cup_{i=1}^N \{ \textrm{t}_i^i \}\)는 이후 frame-wise self-attention layer와 global self-attention layer를 번갈아 배치하는 메인 네트워크 구조를 통해 처리된다.

Alternating-Attention (AA)

저자들은 표준 transformer 디자인에 Alternating-Attention (AA)를 도입하여 transformer가 각 프레임 내 정보와 글로벌 정보에 교대로 attention할 수 있도록 하였다. 구체적으로, frame-wise self-attention은 각 프레임 내의 토큰 \(\textrm{t}_k^I\)에 개별적으로 attention하고, global self-attention은 모든 프레임의 토큰 \(\textrm{t}^I\)에 공동으로 attention한다. 이는 여러 이미지 간의 정보 통합과 각 이미지 내 토큰의 activation 정규화 간의 균형을 이룬다. 이 아키텍처는 cross-attention layer를 사용하지 않고 self-attention layer만 사용한다.

3. Prediction heads

각 입력 이미지 $I_i$에 대해 해당 이미지 토큰 \(\textrm{t}_i^I\)를 추가 카메라 토큰 \(\textrm{t}_i^\textbf{g} \in \mathbb{R}^{1 \times C^\prime}\)과 네 개의 register token \(\textrm{t}_i^R \in \mathbb{R}^{4 \times C^\prime}\)으로 확장한다. 그런 다음, concat된 \((\textrm{t}_i^I, \textrm{t}_i^\textbf{g}, \textrm{t}_i^R)_{i=1}^N\)이 AA transformer로 전달되어 출력 토큰 \((\hat{\textrm{t}}_i^I, \hat{\textrm{t}}_i^\textbf{g}, \hat{\textrm{t}}_i^R)_{i=1}^N\)을 생성한다.

여기서, 첫 번째 프레임의 카메라 토큰과 register token은 다른 모든 프레임과는 별개로 \(\bar{\textrm{t}}^\textbf{g}\)와 \(\bar{\textrm{t}}^R\)로 설정된다.

\[\begin{equation} \textrm{t}_i^\textbf{g}, \textrm{t}_i^R = \begin{cases} \bar{\textrm{t}}^\textbf{g}, \bar{\textrm{t}}^R & \textrm{if} \; i = 1 \\ \bar{\bar{\textrm{t}}}^\textbf{g}, \bar{\bar{\textrm{t}}}^R & \textrm{if} \; i \in [2, \ldots, N] \end{cases} \end{equation}\]

이를 통해 모델은 첫 번째 프레임을 나머지 프레임과 구별하고 첫 번째 카메라의 좌표계에서 3D 예측을 표현할 수 있다. 정제된 카메라 토큰과 정제된 register token은 프레임별로 구분된다. 이는 AA transformer에 카메라 토큰과 register token을 동일한 이미지의 해당 토큰과 일치시킬 수 있도록 하는 frame-wise self-attention layer가 포함되어 있기 때문이다. 일반적인 관행에 따라 출력 register token \(\hat{\textrm{t}}_i^R\)은 삭제되고 \(\hat{\textrm{t}}_i^I\)와 \(\hat{\textrm{t}}_i^\textbf{g}\)는 예측에 사용된다.

좌표계

첫 번째 카메라 \(\textbf{g}_1\)의 좌표계에서 카메라, point map, depth map을 예측한다. 따라서 첫 번째 카메라의 extrinsic 출력은 \(\textbf{q}_1 = [0,0,0,1]\)와 \(\textbf{t}_1 = [0,0,0]\)로 설정된다.

카메라 예측

출력 카메라 토큰 \((\hat{\textrm{t}}_i^\textbf{g})_{i=1}^N\)은 카메라 head에 입력되어 카메라 파라미터 \((\hat{\textbf{g}}^i)_{i=1}^N\)를 예측하는 데 사용된다. 카메라 head는 4개의 추가 self-attention layer와 그 뒤에 오는 linear layer로 구성된다.

Depth map, point map, tracking feature 예측

출력 이미지 토큰 \(\hat{\textrm{t}}_i^I\)는 depth map $D_i$, point map $P_i$, tracking feature $T_i$를 예측하는 데 사용돤다. 구체적으로, \(\hat{\textrm{t}}_i^I\)는 먼저 DPT layer를 사용하여 dense feature map \(F_i \in \mathbb{R}^{C^\prime\prime \times H \times W}\)로 변환된다. 그런 다음, 각 $F_i$는 3$\times$3 convolutional layer를 사용하여 depth map $D_i$와 point map $P_i$에 매핑된다.

또한 DPT head는 tracking head에 대한 입력으로 사용되는 $T_i \in \mathbb{R}^{C \times H \times W}$도 출력한다. 추가로, 각 depth map과 point map에 대해 각각 불확실성 \(\Sigma_i^D \in \mathbb{R}_{+}^{H \times W}\)와 \(\Sigma_i^P \in \mathbb{R}_{+}^{H \times W}\)를 예측한다. 불확실성 맵은 loss에 사용되고 학습 후에는 예측에 대한 모델의 신뢰도에 비례한다.

Tracking

Tracking head $\mathcal{T}$를 구현하기 위해, 저자들은 CoTracker2 아키텍처를 사용하였다. 구체적으로, 쿼리 이미지 $I_q$의 쿼리 포인트 \(\textbf{y}_j\)가 주어졌을 때 (학습 중에는 항상 $q = 1$로 설정), $\mathcal{T}$는 $\textbf{y}$와 동일한 3D 포인트에 대응하는 모든 이미지 $I_i$에서 2D 포인트 집합을 예측한다. 이를 위해, 먼저 쿼리 포인트 \(\textbf{y}_j\)에서 쿼리 이미지의 feature map $T_q$를 bilinear하게 샘플링하여 feature를 얻는다. 이 feature는 다른 모든 feature map $T_{i \ne q}$와 상관 관계를 맺어 correlation map의 집합을 얻는다. 그런 다음, correlation map들은 self-attention layer에서 처리되어 모두 \(\textbf{y}_j\)와 대응하는 최종 2D 포인트 \(\hat{\textbf{y}}_i\)를 예측한다. Tracking head는 입력 프레임의 시간적 순서를 가정하지 않으므로 동영상뿐만 아니라 모든 입력 이미지 집합에 적용될 수 있다.

4. Training

학습 loss

VGGT 모델은 multi-task loss를 사용하여 end-to-end로 학습된다.

\[\begin{aligned} \mathcal{L} &= \mathcal{L}_\textrm{camera} + \mathcal{L}_\textrm{depth} + \mathcal{L}_\textrm{pmap} + \lambda \mathcal{L}_\textrm{track} \\ \mathcal{L}_\textrm{camera} &= \sum_{i=1}^N \| \hat{\textbf{g}}_i - \textbf{g}_i \|_\epsilon \\ \mathcal{L}_\textrm{depth} &= \sum_{i=1}^N \| \Sigma_i^D \odot (\hat{D}_i - D_i) \| + \| \Sigma_i^D \odot (\nabla \hat{D}_i - \nabla D_i) \| - \alpha \log \Sigma_i^D \\ \mathcal{L}_\textrm{pmap} &= \sum_{i=1}^N \| \Sigma_i^P \odot (\hat{P}_i - P_i) \| + \| \Sigma_i^P \odot (\nabla \hat{P}_i - \nabla P_i) \| - \alpha \log \Sigma_i^P \\ \mathcal{L}_\textrm{track} &= \sum_{j=1}^M \sum_{i=1}^N \| \textbf{y}_{j,i} - \hat{\textbf{y}}_{j,i} \| \end{aligned}\]

($\lambda = 0.05$, \(\| \cdot \|_\epsilon\)은 Huber loss, \(\Sigma_i^D\)와 \(\Sigma_i^P\)는 depth와 point map에 대한 신뢰도, \(\textbf{y}_{j,i}\)는 이미지 $I_i$에서의 GT 쿼리 포인트 \(\textbf{y}_j\)에 대한 GT correspondence)

GT 좌표 정규화

장면의 스케일을 조정하거나 글로벌 레퍼런스 좌표계를 변경하더라도 장면의 이미지는 전혀 영향을 받지 않으므로 이러한 변형은 가능한 3D 재구성 결과이다. 저자들은 데이터를 정규화하여 이러한 모호성을 제거하고 표준 선택을 한 다음 transformer에 이 특정 변형을 출력하도록 하였다.

구체적으로, 모든 값을 첫 번째 카메라의 좌표계로 표현한 다음 point map $P$에 있는 모든 3D 포인트의 원점까지의 평균 유클리드 거리를 계산한다. 그런 다음 이 스케일을 사용하여 카메라 translation $\textbf{t}$, point map $P$, depth map $D$를 정규화한다. 중요한 점은 DUSt3R와 달리 transformer의 예측 출력에 이러한 정규화를 적용하지 않는다. 대신 학습 데이터에서 선택한 정규화를 transformer가 학습하도록 한다.

Experiments

• 데이터셋: Co3Dv2, BlendMVS, DL3DV, MegaDepth, Kubric, WildRGB, ScanNet, HyperSim, Mapillary, Habitat, Replica, MVS-Synth, PointOdyssey, Virtual KITTI, Aria Synthetic Environments, Aria Digital Twin
• 구현 디테일
  • 레이어 수: $L = 24$
  • optimizer: AdamW
  • iteration: 16만
  • learning rate: 0.0002 (cosine scheduler, 8K warmup)
  • 각 batch는 2~24개의 프레임을 랜덤 샘플링하여 구성
  • 해상도: 가장 긴 변의 길이가 518, 종횡비는 0.33 ~ 1.0
  • 랜덤하게 color jittering 적용
  • gradient norm clipping threshold: 1.0
  • A100 GPU 64개에서 9일 학습

1. Camera Pose Estimation

다음은 카메라 포즈 추정 성능을 비교한 결과이다. (RealEstate10K, CO3Dv2)

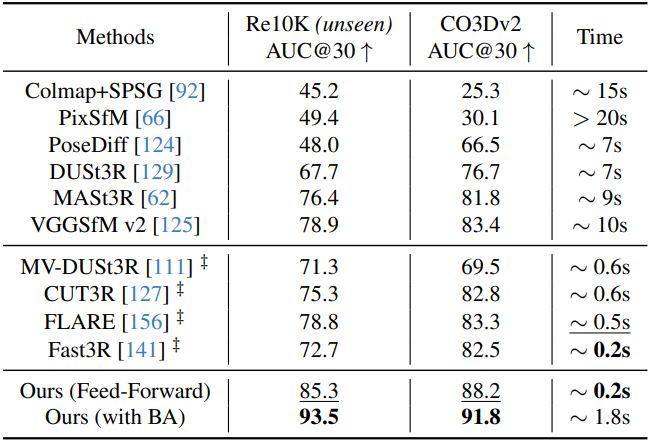
2. Multi-view Depth Estimation

다음은 멀티뷰 깊이 추정 성능을 비교한 결과이다. (DTU)

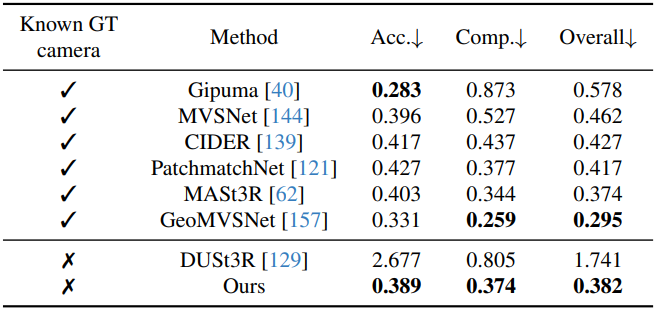
3. Point Map Estimation

다음은 point map 추정 성능을 비교한 결과이다. (ETH3D)

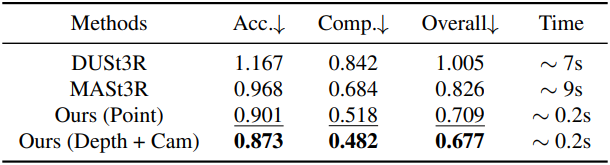
다음은 point map 추정 결과를 시각화 한 것이다.

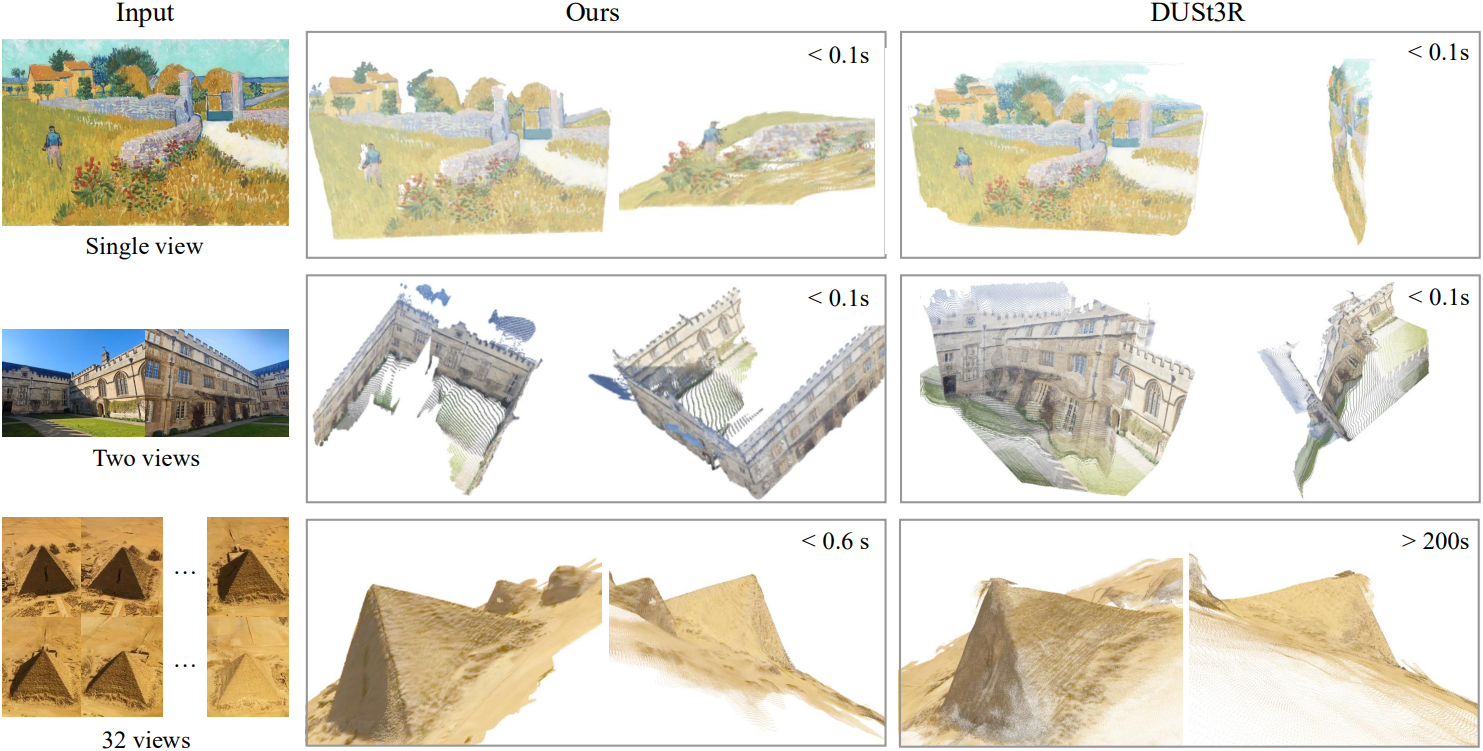
4. Image Matching

다음은 two-view matching 성능을 비교한 결과이다. (ScanNet-1500)

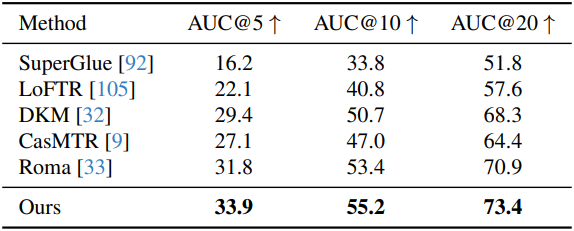
5. Ablation Studies

다음은 (왼쪽) backbone과 (오른쪽) multi-task learning에 대한 ablation 결과이다.

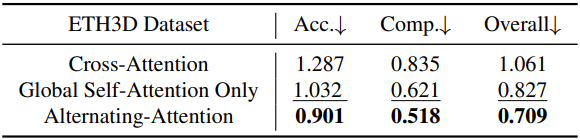
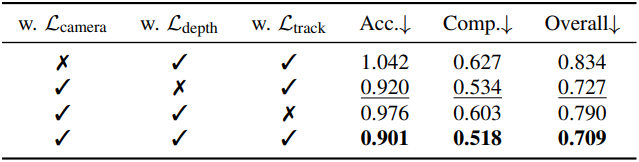
6. Finetuning for Downstream Tasks

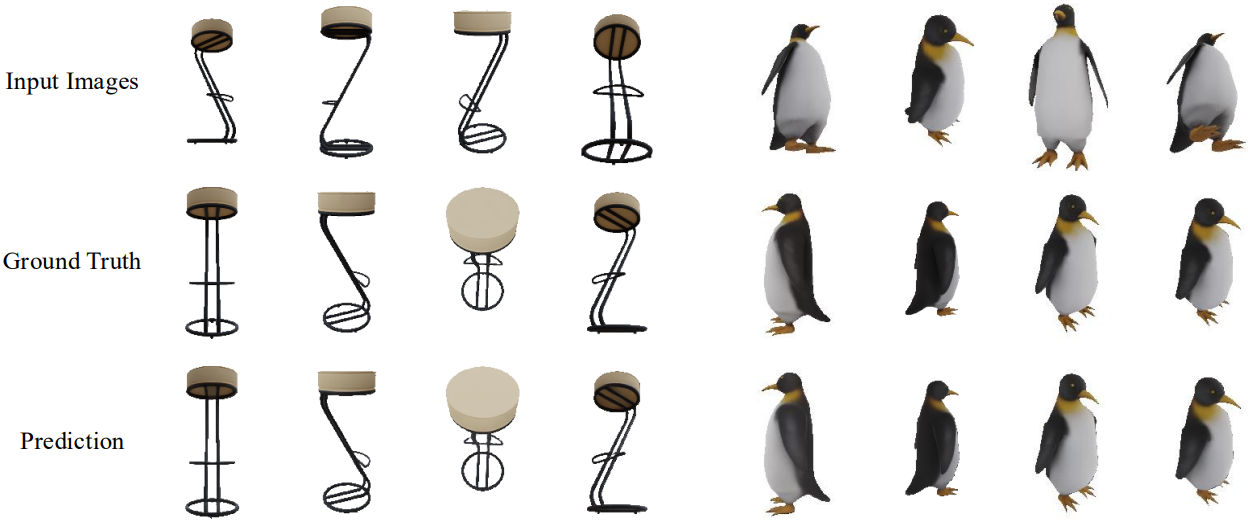
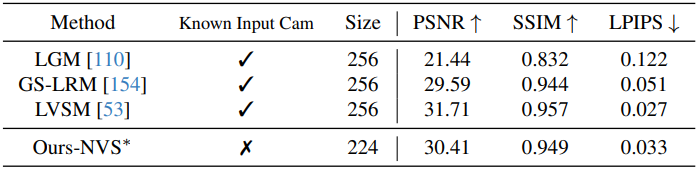
다음은 novel view synthesis에 대한 예시들과 렌더링 품질 비교 결과이다. (GSO)

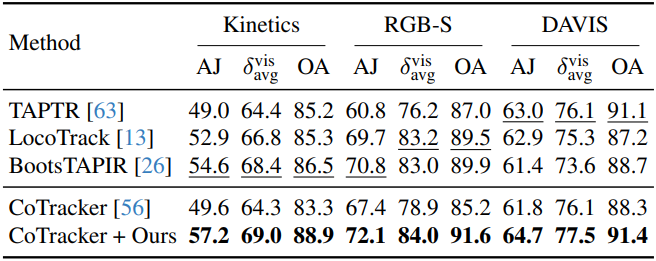
다음은 dynamic point tracking 성능을 비교한 결과이다. (TAP-Vid)

다음은 정적 장면과 동적 장면에 대한 point tracking 예시이다.