[논문리뷰] Variational Diffusion Models

arXiv 2021. [Paper] [Github]
Diederik P. Kingma, Tim Salimans, Ben Poole, Jonathan Ho
Google Research
1 Jul 2021

Introduction

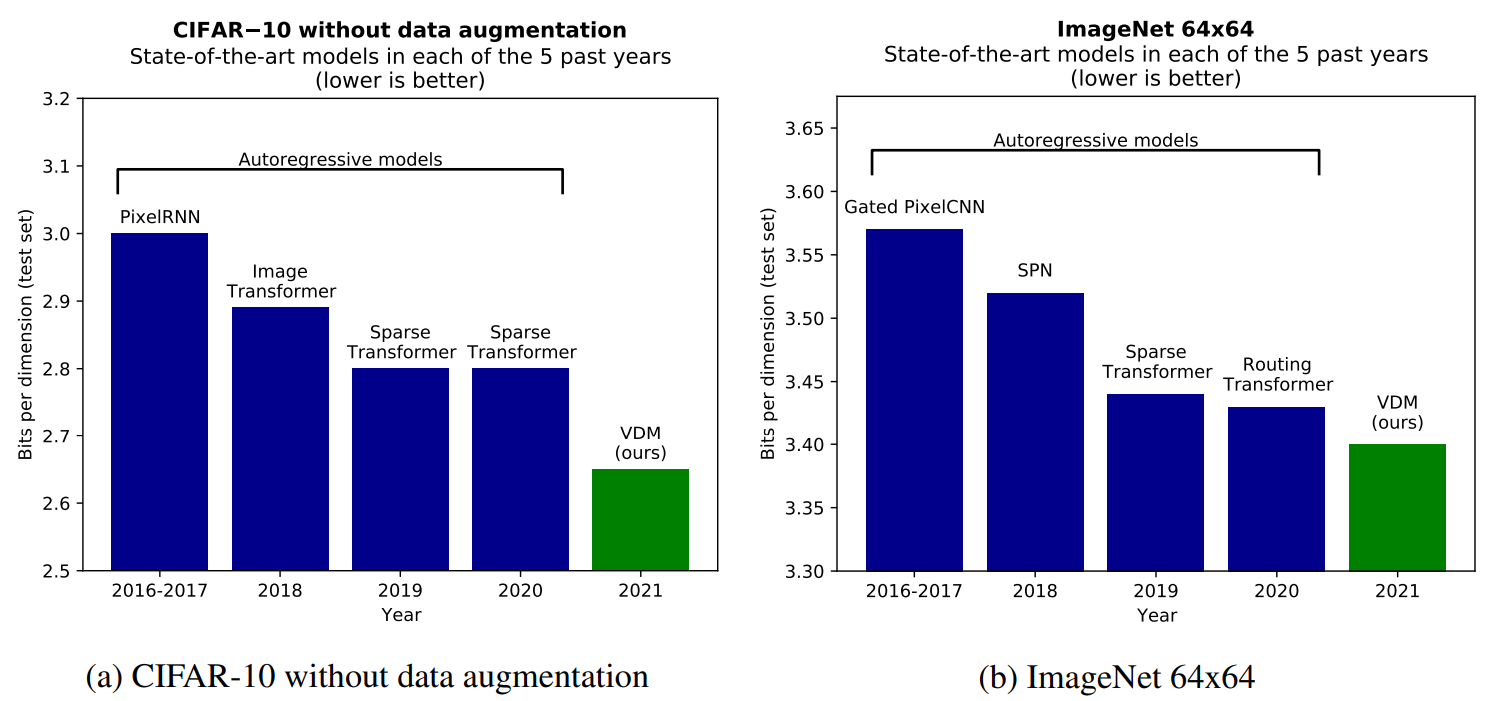
Likelihood 기반의 생성 모델링은 기계 학습의 핵심 task이다. Autoregressive 모델은 위 그림과 같이 tractable한 likelihood와 표현성으로 인해 오랫동안 이 task에서 지배적인 모델 클래스였다. Diffusion model은 최근 perceptual한 품질 측면에서 이미지와 오디오 생성에서 인상적인 결과를 보여주었지만 아직 밀도 추정 벤치마크에서 autoregressive model을 이기지 못했다. 본 논문은 diffusion model이 이 영역에서 autoregressive model의 우위에 도전할 수 있도록 하는 몇 가지 기술적 기여를 한다. 본 논문의 주요 기여는 다음과 같다.

1. 표준 이미지 밀도 추정 벤치마크(CIFAR-10, ImageNet)에서 새로운 state-of-the-art log-likelihood를 달성하는 유연한 diffusion 기반 생성 모델을 소개한다. 이는 Fourier feature를 diffusion model에 통합한다.
2. Diffusion process의 signal-to-noise ratio 측면에서 놀랍도록 간단한 표현을 유도하여 VLB(variational lower bound)를 분석함으로써 diffusion model을 사용하여 밀도 모델링에 대한 이론적 이해를 향상시킨다. 연속적인 시간 (무한한 깊이)에 대해 생성 모델과 생성 모델의 VLB의 새로운 불변성을 증명하고 본 논문의 다양한 diffusion model이 데이터의 사소한 time-dependent rescaling까지 동일하다는 것을 보인다.

Model

1. Forward time diffusion process

본 논문의 출발점은 데이터 $x$로 시작하는 Gaussian diffusion process이며 잠재 변수 $z_t$라 부르는 $x$의 점점 noisy한 시퀀스를 정의한다. 여기서 $t$는 $t = 0$ (가장 덜 noisy)에서 $t = 1$(가장 많이 noisy)까지 실행된다. $x$를 조건으로 하는 $z_t$의 분포는 임의의 $t \in [0,1]$에 대하여 다음과 같다.

\[\begin{equation} q(z_t \vert x) = \mathcal{N} (\alpha_t x, \sigma_t^2 I) \end{equation}\]

$\alpha_t$와 $\sigma_t^2$은 $t$에 대한 양의 스칼라 함수이다. 또한 signal-to-noise ratio (SNR)은

\[\begin{equation} \textrm{SNR}(t) = \frac{\alpha_t^2}{\sigma_t^2} \end{equation}\]

이다. 저자들은 $\textrm{SNR}(t)$가 $t$에 대하여 단조 감소하다고 가정한다. 이것은 $z_t$가 $t$가 증가함에 따라 점점 noisy히디는 개념을 공식화한다. 추가로 $\alpha_t$와 $\sigma_t^2$가 매끄럽다고 가정하여 시간 $t$에 대한 도함수가 유한하다고 가정한다. 이 diffusion process는 variance-preserving diffusion proces를 특별한 경우로 포함하며, 이 때 $\alpha_t = \sqrt{1 - \sigma_t^2}$이다. 또다른 특별한 경우는 variance-exploding diffusion process이며 $\alpha_t^2 = 1$이다. 실험에서는 variance-preserving 버전을 사용한다.

임의의 $t > s$에 대한 분포 $q(z_t \vert z_s)$도 가우시안 분포이다. 임의의 timestep $0 \le s < t < u \le 1$에 대하여 잠재 변수 $(z_s, z_t, z_u)$의 결합 분포는 Markov고, 즉 $q(z_u \vert z_t, z_s) = q(z_u \vert z_t)$이다. 베이즈 정리를 사용하면 임의의 $0 \le s < t \le 1$애 대하여 $q(z_s \vert z_t, x)$도 가우시안 분포임을 보일 수 있다.

2. Noise schedule

기존 연구에서는 noise schedule을 고정된 형태로 사용하였다. 반면, 본 논문에서는

\[\begin{equation} \sigma_t^2 = \textrm{sigmoid}(\gamma_\eta (t)) \end{equation}\]

로 parameterize하여 noise schedule을 학습시킨다. 여기서 $\gamma_\eta (t)$는 파라미터 $\eta$를 가지는 단조 신경망이다.

본 논문의 실험에서는 이산적인 시간이나 연속적인 시간 모두에서 $\alpha_t = \sqrt{1 - \sigma_t^2}$을 사용한다. $\alpha_t^2$와 $\textrm{SNR}(t)$을 $\gamma_\eta (t)$의 함수로 나타낼 수 있다.

\[\begin{equation} \alpha_t^2 = \textrm{sigmoid} (-\gamma_\eta (t)) \textrm{SNR}(t) = \exp (-\gamma_\eta (t)) \end{equation}\]

3. Reverse time generative model

생성 모델은 diffusion process를 반전시켜 정의하고, 시간이 $t = 1$에서 $t = 0$으로 역행하는 latent $z_t$의 시퀀스를 샘플링하는 계층적 생성 모델을 사용한다. 이 시퀀스가 유한 개의 step $T$ 및 $T \rightarrow \infty$에 해당하는 연속 시간 모델로 구성된 경우를 모두 고려한다.

먼저 이산적인 시간을 사용하는 경우, 주어진 유한한 $T$에 대하여 시간을 길이 $\tau = 1/T$로 균일하게 $T$ timestep으로 이산화할 수 있다. $s(i) = (i-1)/T$이고 $t(i) = i/T$라 정의하면 데이터 $x$에 대한 계층적 생성 모델은 다음과 같다.

\[\begin{equation} p(x) = \int_z p(z_1) p(x \vert z_0) \prod_{i=1}^T p(z_{s(i)} \vert z_{t(i)}) \end{equation}\]

Variance preserving diffusion process에서 충분히 작은 $\textrm{SNR}(1)$에 대하여 $q(z_1 \vert x) \approx \mathcal{N} (z_1; 0, I)$이다. 따라서 주변 분포 $z_1$를 가우시안 분포로 모델링한다.

\[\begin{equation} p(z_1) = \mathcal{N} (z_1; 0, I) \end{equation}\]

$p(x \vert z_0)$를 모르는 $q(x \vert z_0)$에 가깝도록 모델링해야 한다. $x_i$와 $z_{0,i}$를 $x$와 $z_0$의 $i$번째 element라 하면 다음과 같이 나타낼 수 있다.

\[\begin{equation} p(x \vert z_0) = \prod_i p(x_i \vert z_{0,i}) \end{equation}\]

여기서 $p(x_i \vert z_{0,i}) \propto q(z_{0,i} \vert x_i)$로 선택하며, $x_i$의 가능한 모든 값의 합을 정규화한 것이다. 충분히 큰 $\textrm{SNR}(0)$에 대하여, likelihood $q(z_0 \vert x)$rk $q(x)$를 압도하므로 $p(x \vert z_0)$는 $q(x \vert z_0)$에 굉장히 가까워진다. 조건부 모델 분포는 다음과 같다.

\[\begin{equation} p(z_s \vert z_t) = q(z_s \vert z_t, x = \hat{x}_\theta (z_t; t)) \end{equation}\]

$q(z_s \vert z_t, x)$와 같지만 원본 데이터 $x$ 대신 denoising model의 출력 $\hat{x}\theta (z_t; t)$를 사용한다. $\hat{x}\theta (z_t; t)$는 $z_t$에서 $x$를 예측한 것이다.

4. Noise prediction model and Fourier features

Denoising model을 신경망으로 parameterize한 noise 예측 모델 $\hat{\epsilon}_\theta (z_t; t)$으로 나타낼 수 있다.

\[\begin{equation} \hat{x}_\theta (z_t; t) = \frac{z_t - \sigma_t \hat{\epsilon}_\theta (z_t; t)}{\alpha_t} \end{equation}\]

기존 연구들의 Diffusion model은 주로 생성된 샘플의 perceptual한 품질에 중점을 두었으며, 이는 생성된 이미지의 대략적인 패턴과 전역 일관성을 강조한다. 여기에서 저자들은 미세한 디테일과 개별 픽셀의 정확한 값에 민감한 likelihood를 최적화한다. 데이터의 미세한 디테일을 포착하기 위해 noise 예측 모델의 입력에 Fourier feature의 세트를 추가할 것을 제안한다.

[-1, 1]로 스케일링된 원본 데이터 $x$에 대하여 $z$를 크기가 비슷한 결과 잠재 변수라고 하자. 그런 다음 $sin(2n \pi z)$와 $\cos(2n \pi z)$ 채널을 추가한다. 여기서 $n$은 정수 범위 \(\{n_{min}, ..., n_{max}\}\)에 대해 실행된다. 이러한 feature는 입력 데이터 $z_t$의 작은 변화를 증폭하는 고주파의 주기 함수이다. Denoising model의 입력에 이러한 feature를 포함하면 특히 학습 가능한 SNR feature와 결합할 때 likelihood가 크게 향상된다. Fourier feature을 autoregressive 모델에 통합할 때는 이러한 개선 사항을 관찰하지 못했다고 한다.

5. Variational lower bound

Likelihood의 variational lower bound (VLB)로 파라미터를 최적화한다.

\[\begin{equation} -\log p(x) \le -\textrm{VLB}(x) = \underbrace{D_{KL} (q(z_1 \vert x) \| p(z_1))}_{\textrm{Prior loss}} + \underbrace{\mathbb{E}_{q(z_0 \vert x)} [- \log p(x \vert z_0)]}_{\textrm{Reconstruction loss}} + \underbrace{\mathcal{L}_T (x)}_{\textrm{Diffusion loss}} \end{equation}\]

Prior loss와 reconstruction loss는 표준 테크닉으로 추정할 수 있다. Diffusion loss는 더 복잡하며 $T$에 의존한다.

Discrete-time model

유한한 $T$의 경우 $s(i) = (i-1)/T, t(i) = i/T$를 사용하며 diffusion loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_T (x) = \sum_{i=1}^T \mathbb{E}_{q(z_{t(i)} \vert x)} D_{KL} [q(z_{s(i)} \vert z_{t(i)}, x) \| p(z_{s(i)} \vert z_{t(i)})] \end{equation}\]

위 식은 다음과 같이 간단하게 만들 수 있다.

\[\begin{equation} \mathcal{L}_T (x) = \frac{T}{2} \mathbb{E}_{\epsilon \sim \mathcal{N} (0, I), i \sim U\{i,T\}} [(\textrm{SNR}(s) - \textrm{SNR} (t)) \| x - \hat{x}_\theta (z_t ; t) \|_2^2] \end{equation}\]

여기서 $z_t = \alpha_t x + \sigma_t \epsilon$이다. 위 식은 임의의 forward diffusion 파라미터 $(\sigma_t, \alpha_t)$에 대한 일반적인 이산 시간 loss이다.

실험에서 사용하는 $\sigma_t$, $\alpha_t$, $\hat{x}_\theta (z_t; t)$를 대입하면 다음과 같다.

\[\begin{equation} \mathcal{L}_T (x) = \frac{T}{2} \mathbb{E}_{\epsilon \sim \mathcal{N} (0, I), i \sim U\{i,T\}} [(\exp(\gamma_\eta (t) - \gamma_\eta (s)) - 1) \| \epsilon - \hat{\epsilon}_\theta (z_t ; t) \|_2^2] \end{equation}\]

여기서 $z_t = \textrm{sigmoid}(-\gamma_\eta (t)) x + \textrm{sigmoid}(\gamma_\eta (t)) \epsilon$이다. 이산 시간의 경우 VLB를 최대화하여 간단하게 $\eta$와 $\theta$를 함께 최적화할 수 있다.

1. More steps leads to a lower loss

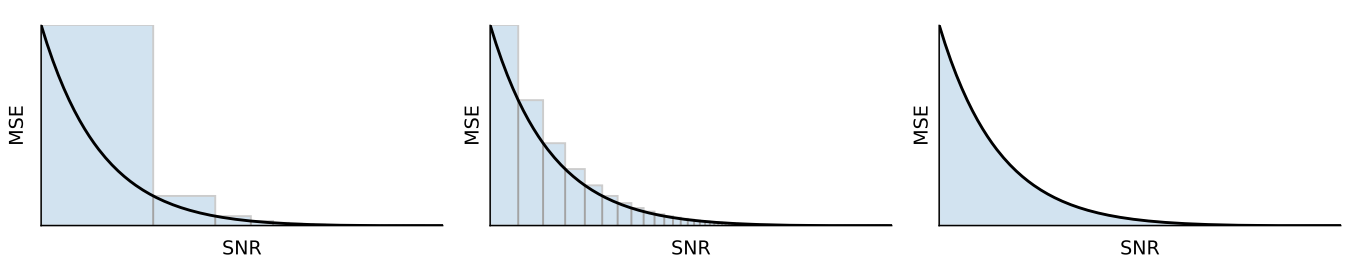
Timestep의 수 $T$가 어떻게 두어야 하는 지, 더 많은 timestep이 VLB가 항상 더 좋은 지 의문점이 생긴다. 저자들은 timestep을 2배로 하였을 때의 diffusion loss \(\mathcal{L}_{2T} (x)\)를 고정된 SNR 함수에 대하여 계산해 보았다. 그 결과 $\hat{x}_\theta$가 충분히 좋은 경우 \(\mathcal{L}_{2T} (x) < \mathcal{L}_T (x)\)라고 하며, 이는 더 큰 timestep에 대하여 VLB가 더 좋아진다는 것이다. 직관적으로 보면 이산 시간에서의 diffusion loss는 연속 시간에서의 적분 값을 리만 상합으로 근사한 것이므로 timestep이 커지면 더 정확하게 근사가 되어 diffusion loss가 감소한다. 아래 그림을 보면 이해하기 쉽다.

Continuous-time model: $T \rightarrow \infty$

더 큰 timestep을 두면 VLB가 좋아지므로 $T \rightarrow \infty$를 생각할 수 있다. $p(z_t)$에 대한 모델은 stochastic differential equation(SDE)를 사용하여 연속 시간 diffusion process로 표현할 수 있다.

$\textrm{SNR}’(t) = d \textrm{SNR(t)} / dt$이고 $z_t = \alpha_t x + \sigma_t \epsilon$라 두면 다음 식이 성립한다.

\[\begin{aligned} \mathcal{L}_\infty (x) = -\frac{1}{2} \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)} \int_0^1 \textrm{SNR}'(t) \| x - \hat{x}_\theta (z_t; t) \|_2^2 dt \\ -\frac{1}{2} \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I), t \sim \mathcal{U}(0,1)} \bigg[ \textrm{SNR}'(t) \| x - \hat{x}_\theta (z_t; t) \|_2^2 \bigg] \end{aligned}\]

위 식은 임의의 forward diffusion 파라미터 $(\sigma_t, \alpha_t)$에 대한 일반적인 연속 시간 loss이다.

실험에서 사용하는 $\sigma_t$, $\alpha_t$, $\hat{x}_\theta (z_t; t)$를 대입하면 다음과 같다.

\[\begin{equation} \mathcal{L}_\infty (x) = \frac{1}{2} \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I), t \sim \mathcal{U} (0,1)} \bigg[ \gamma_\eta'(t) \| \epsilon - \hat{\epsilon}_\theta (z_t; t) \|_2^2 \bigg] \end{equation}\]

$\gamma_\eta’ (t) = d \gamma_\eta (t) / dt$이다. 평가와 최적화에 위 loss의 Monte Carlo estimator를 사용한다.

1. Equivalence of diffusion models in continuous time

$\textrm{SNR}(t)$는 단조성에 의해 가역적이다. 이 가역성에 의해 $t$ 대신 $t = \textrm{SNR}^{-1} (v)$인 $v \equiv \textrm{SNR}(t)$를 사용할 수 있다. $\alpha_v$와 $\sigma_v$가 $\alpha_t$와 $\sigma_t$의 함수라고 하면 $z_v = \alpha_v x + \sigma_v \epsilon$이라 할 수 있다. 비슷하게 noise 예측 모델도 $\tilde{x}\theta (z,v) \equiv \hat{x}\theta (z, \textrm{SNR}^{-1} (v))$로 다시 쓸 수 있다. 연속 시간 loss도 다시 쓸 수 있다.

\[\begin{equation} \mathcal{L}_\infty (x) = \frac{1}{2} \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)} \int_{\textrm{SNR}_\textrm{min}}^{\textrm{SNR}_\textrm{max}} \| x - \tilde{x}_\theta (z_v, v) \|_2^2 dv \end{equation}\]

\(\textrm{SNR}_\textrm{min} = \textrm{SNR}(1)\)이고 \(\textrm{SNR}_\textrm{max} = \textrm{SNR}(0)\)이다.

이 식은 diffusion loss에 $\alpha (t)$와 $\sigma (t)$만 영향을 준다는 것을 보여준다. \(\textrm{SNR}_\textrm{max}\)와 \(\textrm{SNR}_\textrm{min}\)이 주어지면 diffusion model은 $t = 0$과 $t = 1$ 사이에서 함수 $\textrm{SNR}(t)$의 모양에 대하여 불변이다. 따라서 VLB는 끝점을 통해 오직 $\textrm{SNR}(t)$에 의해서만 영향을 받는다.

추가로, 저자들은 생성 모델에 의해 정의된 $p(x)$도 diffusion process에 불변하다는 것을 알아냈다. 구체적으로, $p^A (x)$를 \(\{\alpha_v^A, \sigma_v^A, \tilde{x}_\theta^A\}\)로 정의한 분포이고 $p^B (x)$를 \(\{\alpha_v^B, \sigma_v^B, \tilde{x}_\theta^B\}\)로 정의한 분포라고 하고, 둘 다 동일한 \(\textrm{SNR}_\textrm{max}\)와 \(\textrm{SNR}_\textrm{min}\)을 사용한다고 하자. 그러면 $\tilde{x}\theta^B (z, v) \equiv \tilde{x}\theta^A ((\alpha_v^A / \alpha_v^B )z, v)$일 때 $p^A (x) = p^B (x)$이다. 모든 latent $z_v$에서의 분포도 두 경우가 동일하다. 이는 임의의 두 diffusion model이 같은 \(\{\alpha_v, \sigma_v, \tilde{x}_\theta\}\)를 사용하면 연속 시간에서 동일하다는 것을 의미한다.

2. Weighted diffusion loss

이러한 동일성은 VLB 대신 다음과 같은 weighted diffusion loss를 최적화하는 경우에도 계속 유지된다.

\[\begin{equation} \mathcal{L}_\infty (x, w) = \frac{1}{2} \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)} \int_{\textrm{SNR}_\textrm{min}}^{\textrm{SNR}_\textrm{max}} w(v) \| x - \tilde{x}_\theta (z_v, v) \|_2^2 dv \end{equation}\]

$w(v)$는 일반적으로 증가하는 가중치 함수로, VLB와 비교했을 때 더 noisy한 데이터를 강조하여 perceptual한 생성 품질을 개선할 수 있다.

3. Variance minimization

연속 시간 loss의 Monte Carlo estimator의 분산을 낮추면 일반적으로 최적화의 효율성이 개선된다. 저자들은 $t$에 대한 low-discrepancy sampler을 사용하여 분산을 상당히 줄였다. 또한 앞에서 보인 불변성에 의해 loss의 estimator의 분산을 최소화하도록 끝점 사이의 schedule을 최적화할 수 있다.

Experiments

1. Likelihood and samples

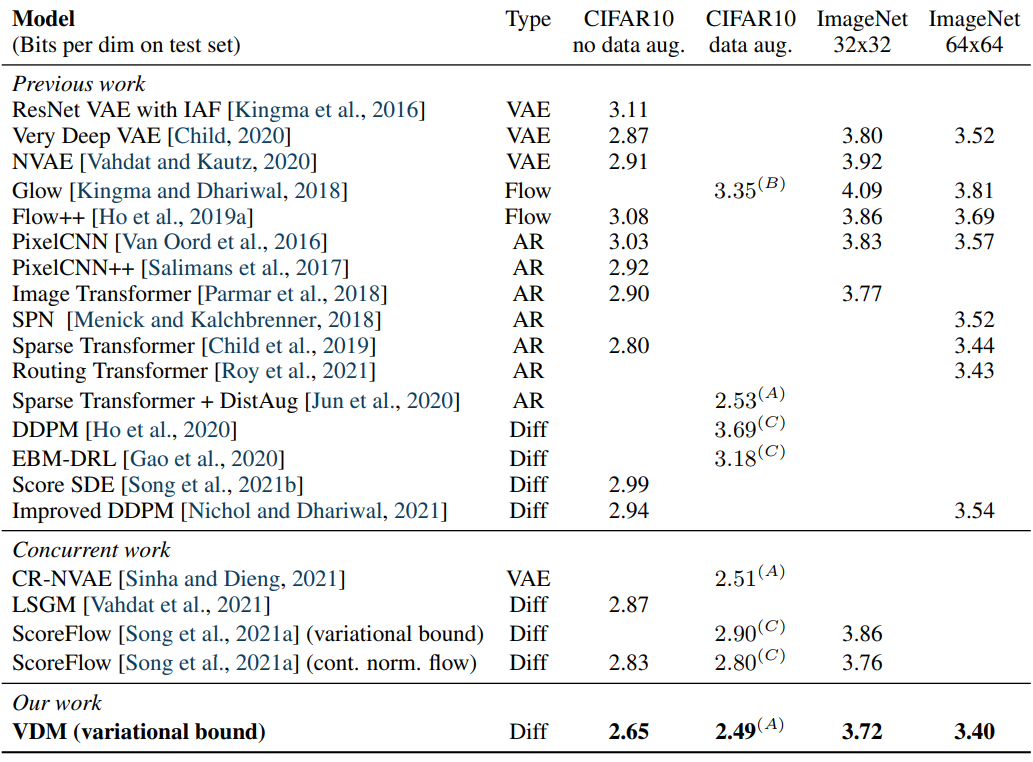
다음 표는 CIFAR-10 데이터셋과 downsmapling된 ImageNet 데이터셋에 대한 결과이다.

다음은 ImageNet 64$\times$64 모델이 출력한 unconditional 샘플이다. 연속 시간에서 학습하고 $T = 1000$으로 생성했다고 한다.

2. Ablations

다음 표는 이산 시간과 연속 시간에 대한 비교 결과이다. BPD는 bits per dimension이다.

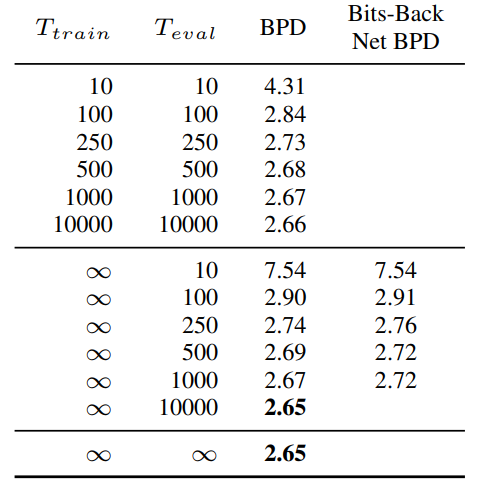
작은 수의 step으로 모델을 평가하는 경우 이산적으로 학습된 모델이 VLB를 최소화하도록 diffusion schedule을 학습하여 성능이 더 좋다. 반면, 앞에서 이론적으로 논의한 것과 갗이 더 많은 step이 실제로 더 나은 likelihood를 제공한다는 것을 실험적으로 확인할 수 있었다. $T$가 커지면 연속적으로 학습된 모델이 분산을 최소화하도록 diffusion schedule을 학습하여 성능이 더 좋아진다.

분산을 최소화하는 것은 연속 모델의 학습이 빠르게 하는 데도 도움이 된다.

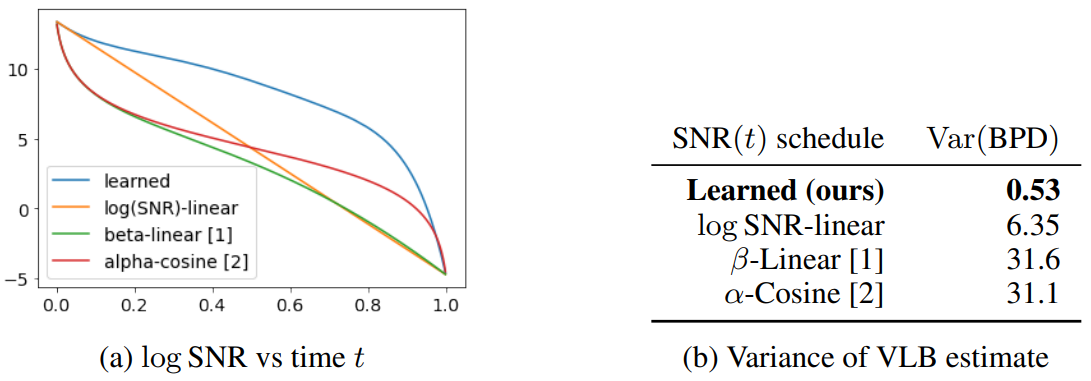
오른쪽 표에서 본 논문의 모델이 baseline과 비교했을 때 연속 시간에서 분산을 굉장히 많이 감소시키는 것을 볼 수 있다. 왼쪽 그림에서는 이 효과가 어떻게 가능한 지를 보여준다. 다른 schedule과 비교했을 때 본 논문의 schedule은 높은 $\textrm{SNR}(t)$과 낮은 $\sigma_t^2$ 범위 더 많은 시간을 사용한다.

다음은 본 논문의 모델에 Fourier feature를 포함할 때와 포함하지 않을 때의 학습 곡선을 보여준다.

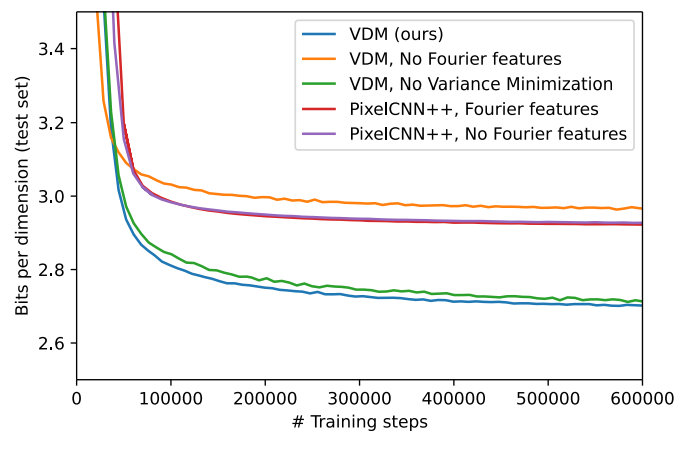
3. Lossless compression

고정된 $T_{eval}$에 대하여, 본 논문의 이산 시간에서의 diffusion model은 계층적 잠재 변수 모델이며, bits-back coding을 사용한 무손실 압축 알고리즘이 된다. 무손실 압축의 개념을 증명하기 위해 비대칭 숫자 시스템에 기반한 bits-back coding의 BPD를 측정하였다고 한다. 이는 이산 시간과 연속 시간에 대한 비교 표의 “Bits-Back Net BPD” 항목을 보면 알 수 있다.