[논문리뷰] Gaussian Splatting with NeRF-based Color and Opacity
arXiv 2023. [Paper] [Github]
Dawid Malarz, Weronika Smolak, Jacek Tabor, Sławomir Tadeja, Przemysław Spurek
Jagiellonian University | University of Cambridge
21 Dec 2023
Introduction
NeRF 아키텍처는 정적 장면에서 새로운 시점의 선명한 렌더링을 생성하는 데 탁월하다. 그러나 주로 객체 모양을 신경망 가중치로 인코딩하는 데 시간이 많이 걸리는 프로세스에서 비롯되는 몇 가지 제한 사항에 직면한다. 실제로 NeRF 모델을 사용한 학습 및 inference에는 오랜 시간이 걸릴 수 있으므로 실시간 애플리케이션에는 종종 비실용적이다.
이에 비해 Gaussian Splatting(GS)은 더 빠른 학습 및 inference로 유사한 품질의 렌더링을 제공한다. 이는 GS가 신경망을 필요로 하지 않기 때문에 발생하는 결과이다. 일련의 Gaussian 분포로 3D 객체에 대한 정보를 인코딩한다. 그러면 이러한 Gaussian을 기존 메시와 유사한 방식으로 사용할 수 있다. 결과적으로, GS는 예를 들어 동적 장면을 모델링해야 할 때 신속하게 개발될 수 있다. 불행하게도 GS는 수십만 개의 Gaussian들이 필요하기 때문에 컨디셔닝하기가 어렵다. NeRF와 GS 등 두 가지 렌더링 방법 모두 다양한 장단점을 가지고 있다.
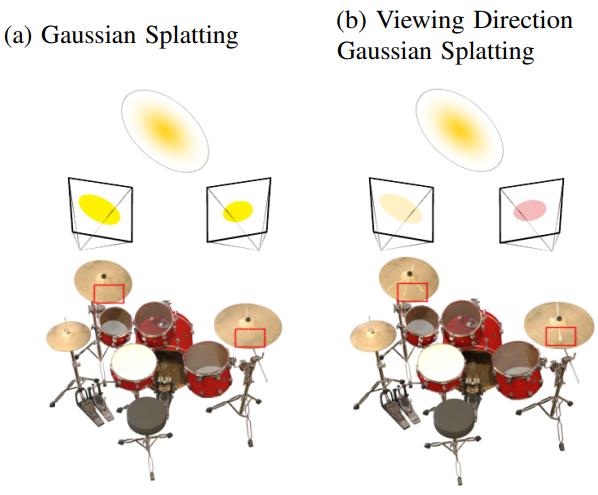
본 논문에서는 3D 객체 모양의 GS 표현을 사용하고 동시에 NeRF 기반 색상 및 불투명도 인코딩을 사용하는 새로운 하이브리드 접근 방식인 Viewing Direction Gaussian Splatting(VDGS)를 제시하였다. 본 논문의 모델은 학습 가능한 위치(Gaussian 평균), 모양(Gaussian 공분산), 색상, 불투명도를 갖춘 Gaussian 분포와 보는 방향과 함께 Gaussian 파라미터를 사용하여 색상과 불투명도에 대한 변화를 생성하는 신경망을 사용한다.
Viewing Direction Gaussian Splatting
NeRF representation of 3D objects
NeRF는 신경망을 사용하여 복잡한 3D 장면을 표현하기 위한 모델이다. NeRF는 공간 위치 $\mathbf{x} = (x, y, z)$와 보는 방향 $\mathbf{d} = (\theta, \psi)$를 포함하는 5D 좌표를 입력으로 사용하고 방출된 색상 $\mathbf{c} = (r, g, b)$와 볼륨 밀도 $\sigma$를 리턴한다.
이미지를 통과하는 광선의 앙상블이 생성되고, 신경망으로 표현되는 3D 객체와 상호 작용한다. 관찰된 색상과 깊이를 포함한 이러한 상호 작용은 신경망을 학습시켜 물체의 모양과 외형을 정확하게 표현하는 데 사용된다. NeRF는 MLP 네트워크를 사용하여 이 3D 객체를 근사화한다.
\[\begin{equation} \mathcal{F}_\textrm{NeRF} (\mathbf{x}, \mathbf{d}; \Theta) = (\mathbf{c}, \sigma) \end{equation}\]MLP 파라미터 $\Theta$는 학습 중에 최적화되어 렌더링된 이미지와 주어진 데이터셋의 레퍼런스 이미지 간의 불일치를 최소화한다. 결과적으로 MLP 네트워크는 3D 좌표를 입력으로 사용하고 지정된 방향의 색상과 함께 밀도 값을 출력한다.
NeRF의 loss는 고전적인 볼륨 렌더링에서 영감을 받았다. 장면을 통과하는 모든 광선의 색상을 렌더링한다. 볼륨 밀도 $\sigma(x)$는 광선의 differential probability로 해석될 수 있다. 카메라 광선 $\mathbf{r}(t) = \mathbf{o} + t\mathbf{d}$($\mathbf{o}$는 광선 원점, $\mathbf{d}$는 방향)의 예상 색상 $C(\mathbf{r})$은 적분으로 계산할 수 있지만 실제로는 계층적 샘플링(stratified sampling)을 사용하여 수치적으로 추정한다. Loss는 단순히 렌더링된 픽셀 색상과 실제 픽셀 색상 간의 총 제곱 오차이다.
\[\begin{equation} \mathcal{L} = \sum_{\mathbf{r} \in R} \| \hat{C} (\mathbf{r}) - C (\mathbf{r}) \|_2^2 \end{equation}\]여기서 $R$은 각 batch의 광선들이고, $C(\mathbf{r})$과 $\hat{C}(\mathbf{r})$은 각각 광선 $\mathbf{r}$에 대한 ground truth 색상과 예측된 RGB 색상이다. 예측된 RGB 색상 $\hat{C}(\mathbf{r})$은 다음 식을 사용하여 얻을 수 있다.
\[\begin{equation} \hat{C}(\mathbf{r}) = \sum_{i=1}^N T_i (1 - \exp (-\sigma_i \delta_i)) \mathbf{c}_i \\ \textrm{where} \quad T_i = \exp (-\sum_{j=1}^{i-1} \sigma_i \delta_i) \end{equation}\]여기서 $N$은 샘플 수, $\delta_i$는 인접한 샘플 사이의 거리, $\sigma_i$는 샘플 $i$의 불투명도이다. \((\mathbf{c}_i , \sigma_i)\) 값들에서 $\hat{C}(\mathbf{r})$을 계산할 수 있는 이 함수는 쉽게 미분 가능하다.
신경망에서 3D 객체를 표현하는 이러한 접근 방식은 신경망의 용량이나 카메라 광선이 장면 형상과 교차하는 위치를 정확하게 찾는 어려운 task로 인해 종종 한계에 직면한다. 결과적으로 NeRF 표현에서 고해상도 이미지를 생성하려면 계산 비용이 많이 드는 ray marching이 필요하며, 이는 실시간 사용을 방해할 수 있다.
Gaussian Splatting
Gaussian Splatter(GS)는 위치(평균), 공분산 행렬, 불투명도, spherical harmonics(SH)를 통해 표현되는 색상으로 정의된 3D Gaussian들을 통해 3D 장면을 모델링한다.
GS 알고리즘은 3D Gaussian 파라미터(ex. 위치, 공분산, 불투명도, SH 색상)의 일련의 최적화 단계를 통해 표현을 생성한다. GS 효율성의 핵심은 Gaussian 들의 projection을 사용하는 렌더링 프로세스입이다.
GS에서는 dense한 3D Gaussian 집합을 사용한다.
\[\begin{equation} \mathcal{G} = \{(\mathcal{N}(m_i, \Sigma_i), \sigma_i, c_i)\}_{i=1}^n \end{equation}\]여기서 $m_i$, $\Sigma_i$, $\sigma_i$, $c_i$는 각각 $i$번째 Gaussian의 위치, 공분산, 불투명도, SH 색상이다.
GS 최적화는 생성된 이미지를 렌더링하고 수집된 데이터의 학습 뷰와 비교하는 사이클을 기반으로 한다. 불행하게도 3D에서 2D로의 projection은 잘못된 형상 배치로 이어질 수 있다. 따라서 GS 최적화는 형상이 잘못 배치된 경우 형상을 생성, 파괴 및 이동할 수 있어야 한다. 3D Gaussian 공분산 파라미터의 품질은 표현의 간결성을 위해 필수적아다. 큰 균질한 영역은 적은 수의 큰 Gaussian으로 캡처할 수 있기 때문이다.
GS는 제한된 수의 포인트로 시작한 다음 새로운 Gaussian들을 만들고 불필요한 Gaussian들을 제거하는 전략을 사용한다. 100번의 iteration마다 GS는 특정 한도보다 불투명도가 낮은 Gaussian들을 제거한다. 동시에 3D 공간의 비어 있는 영역에 새로운 Gaussian들이 생성되어 빈 공간을 채운다. GS의 최적화 프로세스는 복잡하지만 강력한 구현과 CUDA 커널 사용 덕분에 매우 효과적으로 학습할 수 있다.
Viewing Direction Gaussian Splatting
본 논문의 접근 방식에서는 GS를 사용하여 3D 모양을 모델링하고 NeRF 기반 신경망은 색상과 불투명도를 생성한다. 모델은 Gaussian Splatting 표현 $\mathcal{G}$와 MLP \(\mathcal{F}_\textrm{VDGS}\)으로 구성된다.
\[\begin{equation} \mathcal{G} = \{(\mathcal{N}(m_i, \Sigma_i), \sigma_i, c_i)\}_{i=1}^n \\ \mathcal{F}_\textrm{VDGS} (m, \Sigma, c, \mathbf{d}; \Theta) = \Delta \sigma (\mathbf{d}) \end{equation}\]이는 Gaussian 분포와 보는 방향 $\mathbf{d}$을 사용하여 색상 업데이트 $\Delta \mathbf{c}(\mathbf{d})$와 볼륨 밀도 업데이트 $\Delta \sigma (\mathbf{d})$를 리턴한다. 모델은 보는 방향에 따라 색상과 불투명도를 변경하도록 학습되었다.
최종 Viewing Direction Gaussian Splatting(VDGS) 모델은 다음과 같다.
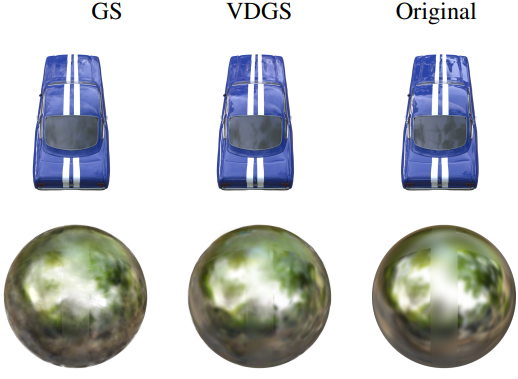
\[\begin{equation} (\mathcal{G}, \mathcal{F}_\textrm{VDGS}) = \{(\mathcal{N}(m_i, \Sigma_i), \sigma_i \cdot \Delta \sigma_i (\mathbf{d}), \mathbf{c}_i)\}_{i=1}^n \\ \textrm{where} \quad \Delta \sigma_i (\mathbf{d}) = \mathcal{F}_\textrm{VDGS} (m_i, \Sigma_i, c_i, \mathbf{d}) \end{equation}\]실제로 GS와 NeRF의 두 가지 구성 요소가 있다. GS는 물체의 모양과 색상을 생성하는 데 사용된다. 모든 Gaussian들은 색상과 투명도를 가지며 보는 방향에 영향을 받지 않는다. GS 덕분에 3D 객체의 보편적인 색상을 모델링할 수 있다. 카메라 위치에 따라 NeRF 구성 요소는 개체에 사소한 색상 변경과 투명도를 추가할 수 있다. VDGS는 보는 방향에 따른 변경 사항을 추가할 수 있다. 따라서 물체의 빛 반사와 투명도를 모델링할 수 있다.
Experiments
Tanks and Temples
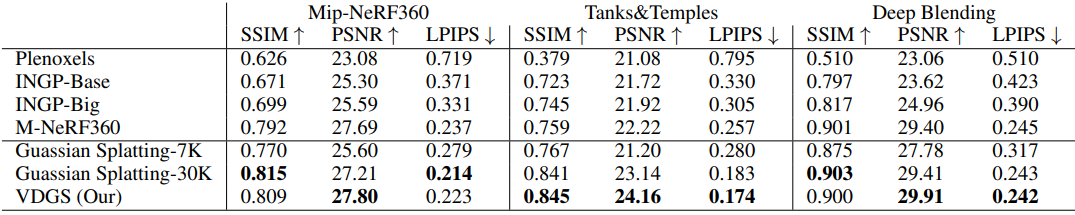

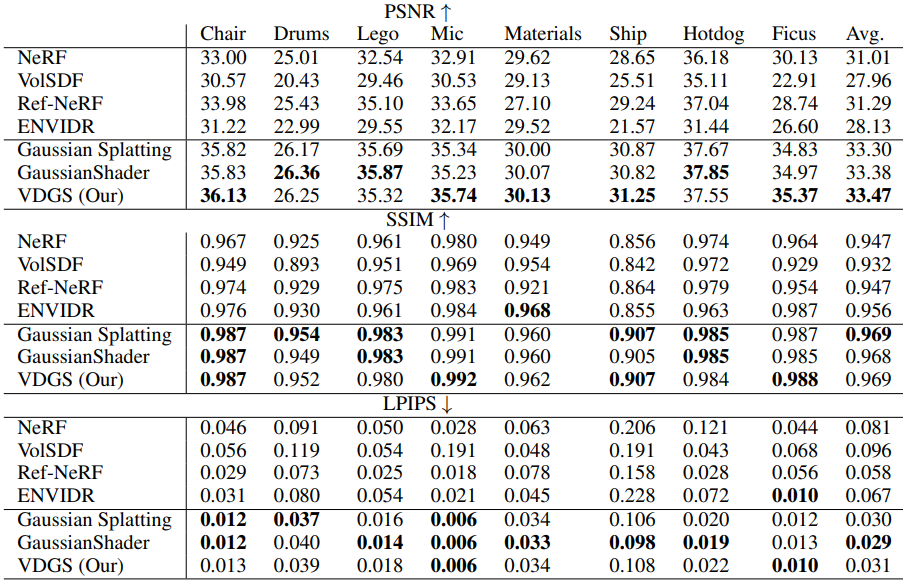
NeRF Synthetic

Shiny Blender