[논문리뷰] Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction
NeurIPS 2024 (Oral). [Paper] [Github]
Keyu Tian, Yi Jiang, Zehuan Yuan, Bingyue Peng, Liwei Wang
Peking University | Bytedance Inc
3 Apr 2024

Introduction
Autoregressive (AR) LLM의 핵심은 self-supervised learning 전략으로, 시퀀스에서 다음 토큰을 예측하는 간단한 접근 방식이다. 대규모 AR 모델의 성공은 확장성(scalability)과 일반화 가능성(generalizabilty)을 강조했다. Scalability는 더 작은 모델에서 대규모 모델의 성능을 예측하여 더 나은 리소스 할당을 안내하며, generalizabilty는 다양하고 처음 보는 task에 대한 모델의 적응성을 강조한다. 이러한 속성은 레이블 없는 방대한 데이터에서 학습하는 AR 모델의 잠재력을 보여준다.
컴퓨터 비전 분야는 scalability와 generalizabilty를 모방하고자 대규모 AR 모델을 개발하기 위해 노력해 왔다. VQGAN과 DALL-E는 이미지 생성에서 AR 모델의 잠재력을 보여주었다. 이러한 모델들은 visual tokenizer를 사용하여 continuous한 이미지를 2D 토큰 그리드로 discretize한 다음 AR 학습을 위해 1D 시퀀스로 flatten한다. 이는 순차적 언어 모델링 프로세스를 반영한다. 그러나 이러한 모델의 scaling law는 여전히 충분히 탐구되지 않았으며, 성능이 diffusion model보다 상당히 뒤떨어져 있다.
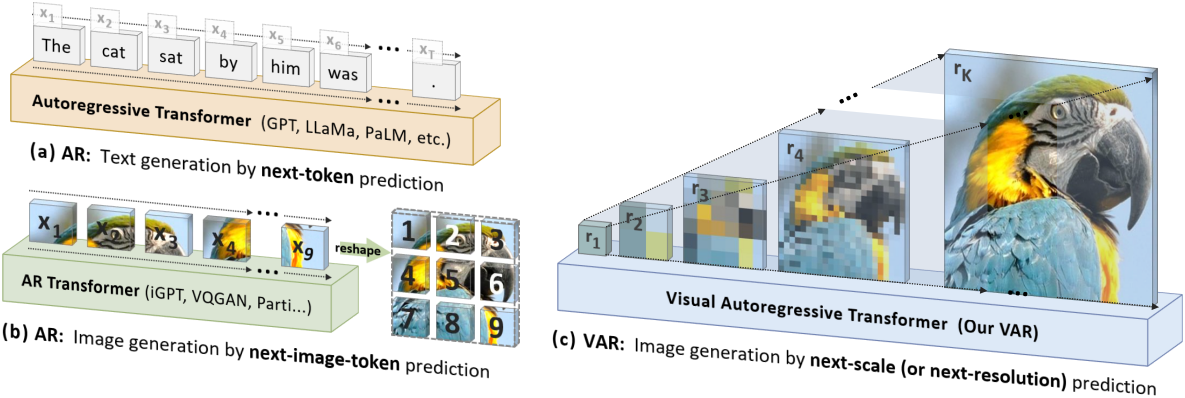
AR 모델링은 데이터의 순서를 정의해야 한다. 인간은 일반적으로 계층적 방식으로 이미지를 인식하거나 생성하여 먼저 글로벌한 구조를 포착한 다음 로컬한 디테일을 포착한다. 이러한 멀티스케일, coarse-to-fine 특성은 이미지에 대한 “순서”를 제안한다. 또한 이미지에 대한 AR 학습을 “next-scale prediction”으로 정의하여 기존의 “next-token prediction”에서 벗어났다.
본 논문의 접근 방식은 이미지를 멀티스케일 token map으로 인코딩하는 것으로 시작한다. 그런 다음 AR 프로세스는 1$\times$1 token map에서 시작하여 점진적으로 해상도가 확장된다. 각 단계에서 transformer는 이전의 모든 token map을 조건으로 다음 고해상도 token map을 예측한다. 이 방법론을 Visual AutoRegressive (VAR) 모델링이라고 한다.
VAR은 GPT-2와 유사한 transformer 아키텍처를 직접 활용한다. ImageNet 256$\times$256 벤치마크에서 VAR은 기존 AR 방법들을 크게 개선하여 1.73의 FID와 350.2의 IS를 달성했으며 inference 속도는 20배 더 빠르다. 특히 VAR은 이미지 품질, 데이터 효율성, inference 속도, scalability 측면에서 Stable Diffusion 3와 Sora에서 사용하는 Diffusion Transformer (DiT)를 능가한다. VAR 모델은 또한 LLM에서 볼 수 있는 것과 유사한 scaling law를 보인다.
Method
1. Preliminary: autoregressive modeling via next-token prediction
Formulation
Discrete한 토큰의 시퀀스 $x = (x_1, x_2, \ldots, x_T)$를 고려하자. 여기서 $x_t \in [V]$는 크기가 $V$인 vocabulary에서 나온 정수이다. Next-token AR은 현재 토큰 $x_t$를 관찰할 확률이 $x_t$의 prefix $(x_1, x_2, \ldots, x_{t−1})$에만 의존한다고 가정한다. 이 단방향 토큰 종속성 가정은 시퀀스 $x$의 likelihood의 인수분해를 허용한다.
\[\begin{equation} p (x_1, x_2, \ldots, x_T) = \prod_{t=1}^T p (x_t \vert x_1, x_2, \ldots, x_{t-1}) \end{equation}\]데이터셋에 대해 \(p_\theta (x_t \vert x_1, x_2, \ldots, x_{t-1})\)를 최적화하여 AR model $p_\theta$를 학습시킬 수 있다. 이것은 “next-token prediction”으로 알려져 있으며, 학습된 $p_\theta$는 새로운 시퀀스를 생성할 수 있다.
Tokenization
이미지는 본질적으로 2D의 continuous한 신호이다. Next-token prediction을 통해 이미지에 AR 모델링을 적용하려면 이미지를 여러 개의 discrete한 토큰으로 tokenize하고, 단방향 모델링을 위해 1D 토큰 순서를 정의해야 한다. Tokenization의 경우, VQVAE와 같은 quantize된 오토인코더를 사용하여 이미지 feature map $f \in \mathbb{R}^{h \times w \times C}$를 이산 토큰 $q \in [V]^{h \times w}$로 변환하는 경우가 많다.
\[\begin{equation} f = \mathcal{E} (I), \quad q = \mathcal{Q} (f) \end{equation}\]($I$는 이미지, $\mathcal{E}(\cdot)$는 인코더, $\mathcal{Q}(\cdot)$는 quantizer)
Quantizer는 일반적으로 $V$개의 벡터들을 포함하는 학습 가능한 codebook $Z \in \mathbb{R}^{V \times C}$를 포함한다. Quantization 프로세스 $q = \mathcal{Q}(f)$는 각 feature 벡터 $f^{(i,j)}$를 가장 거리가 가까운 code의 인덱스 $q^{(i,j)}$로 매핑한다.
\[\begin{equation} q^{(i,j)} = \left( \underset{v \in [V]}{\arg \min} \; \| \textrm{lookup} (Z, v) - f^{(i,j)} \|_2 \right) \in [V] \end{equation}\]여기서 $\textrm{lookup}(Z, v)$는 codebook $Z$에서 $v$번째 벡터를 취하는 것을 의미한다. Quantize된 오토인코더를 학습시키기 위해 $Z$는 모든 $q^{(i,j)}$에 의해 조회되어 원래 $f$의 근사치인 $\hat{f}$를 얻는다. 그런 다음 디코더 $\mathcal{D}(\cdot)$를 사용하여 $\hat{f}$에서 새 이미지 $\hat{I}$를 재구성하고 loss $\mathcal{L}$을 최소화한다.
\[\begin{aligned} \hat{f} &= \textrm{lookup} (Z, q), \qquad \hat{I} = \mathcal{D} (\hat{f}) \\ \mathcal{L} &= \| I - \hat{I} \|_2 + \| f - \hat{f} \|_2 + \lambda_P \mathcal{L}_\textrm{P} (I, \hat{I}) + \lambda_G \mathcal{L}_G (I, \hat{I}) \end{aligned}\](\(\mathcal{L}_P\)는 perceptual loss, \(\mathcal{L}_G\)는 GAN의 discriminator loss)
오토인코더 \(\{\mathcal{E}, \mathcal{Q}, \mathcal{D}\}\)가 완전히 학습되면 이미지를 tokenize하여 이후 단방향 AR 모델을 학습시키는 데 사용된다.
$q \in [V]^{h \times w}$의 이미지 토큰은 2차원 그리드에 배열된다. 단방향 AR 학습의 경우 이미지 토큰의 순서를 명시적으로 정의해야 한다. 이전 AR 방법은 다양한 전략을 사용하여 $q$의 2차원 그리드를 1차원 시퀀스 $x = (x_1, \ldots, x_{h \times w})$로 flatten한다. Flatten되고 나면 데이터셋에서 시퀀스 $x$를 추출한 다음 AR 모델을 학습하여 next-token prediction을 통해 likelihood를 최대화할 수 있다.
Discussion
위의 tokenizing and flattening 접근 방식은 이미지에 대한 next-token AR 학습을 가능하게 하지만 몇 가지 문제점을 야기한다.
- 수학적 전제 위반: VQVAE에서 인코더는 일반적으로 모든 $i, j$에 대해 상호 종속적인 feature 벡터 $f^{(i,j)}$를 갖는 이미지 feature map $f$를 생성한다. 따라서 quantization과 flattening 후 토큰 시퀀스 $(x_1, \ldots, x_{h \times w})$는 양방향 상관 관계를 유지한다. 이는 각 토큰 $x_t$가 prefix $(x_1, \ldots, x_{t−1})$에만 의존해야 한다는 AR 모델의 단방향 종속성 가정과 모순된다.
- 일부 zero-shot 일반화를 수행할 수 없음: 이미지 AR 모델링의 단방향적 특성은 양방향 추론이 필요한 task에서 generalizabilty를 제한한다. 예를 들어, 이미지의 하단 부분을 감안하여 상단 부분을 예측할 수 없다.
- 구조적 저하: Flattening은 이미지 feature map에 내재된 공간적 locality를 방해한다. 예를 들어, 토큰 $q^{(i,j)}$와 4개의 이웃 $q^{(i \pm 1,j)}$, $q^{(i,j \pm 1)}$은 긴밀하게 상관관계가 있다. 이 공간적 관계는 선형 시퀀스 $x$에서 손상되며, 단방향 제약이 이러한 상관관계를 감소시킨다.
- 비효율성: 기존의 self-attention transformer를 사용하여 이미지 토큰 시퀀스 $x = (x_1, \ldots, x_{n \times n})$을 생성하면 $\mathcal{O}(n^2)$의 AR step과 $\mathcal{O}(n^6)$의 계산 비용이 발생한다.
2. Visual autoregressive modeling via next-scale prediction
Reformulation
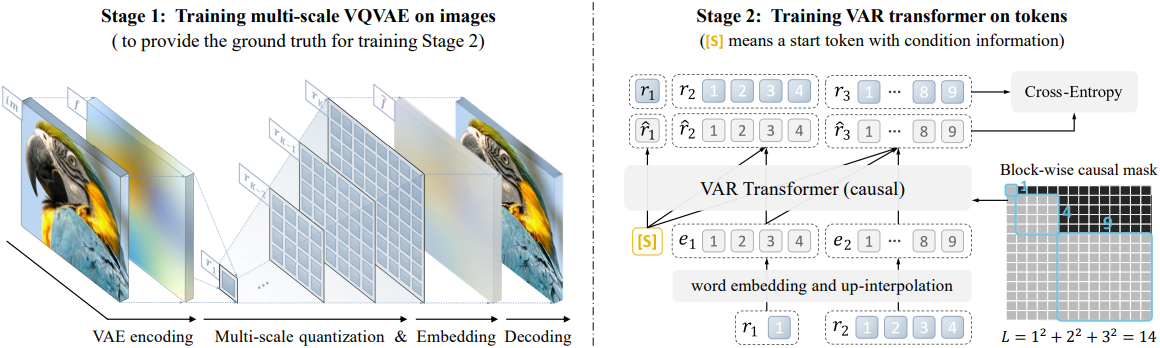
본 논문은 “next-token prediction”에서 “next-scale prediction” 전략으로 전환하여 이미지에 대한 AR 모델링을 재구성하였다. 여기서 AR 단위는 하나의 토큰이 아니라 전체 token map이다.
Feature map $f \in \mathbb{R}^{h \times w \times C}$를 $K$개의 멀티스케일 token map $(r_1, r_2, \ldots r_K)$으로 quantize하는 것으로 시작한다. 각 token map은 점점 더 높은 해상도 $h_k \times w_k$를 가지며, $r_K$는 원래 feature map의 해상도 $h \times w$와 일치한다. AR likelihood는 다음과 같다.
\[\begin{equation} p (r_1, r_2, \ldots, r_K) = \prod_{k=1}^K p (r_k \vert r_1, r_2, \ldots, r_{k-1}) \end{equation}\]여기서 각 AR 단위 $r_k \in [V]^{h_k \times w_k}$는 $h_k \times w_k$개의 토큰을 포함하는 scale $k$의 token map이다. $k$번째 AR step 동안, $r_k$의 모든 토큰에 대한 분포는 $r_k$의 prefix와 연관된 $k$번째 위치 임베딩 map에 따라 병렬로 생성된다. 이 “next-scale prediction” 방법론은 visual autoregressive modeling (VAR)으로 정의된다. VAR의 학습에서 block별 casual attention mask를 사용하여 각 $r_k$가 prefix $r_{\le k}$에만 attention할 수 있도록 한다. Inference를 하는 동안 kv-caching을 사용할 수 있으며 마스크가 필요하지 않다.
Discussion
VAR은 이전에 언급된 세 가지 문제를 다음과 같이 해결한다.
- 각 $r_k$가 prefix에만 의존하도록 제한하면 수학적 전제가 충족된다. 이 제약은 인간의 시각적 인식이나 예술적인 그림의 자연스러운 coarse-to-fine 특성과 일치하므로 허용된다.
- VAR에 flattening 연산이 없고, 각 $r_k$의 토큰이 완전히 상관되어 있기 때문에 공간적 locality는 보존된다. 또한 멀티스케일 디자인은 공간 구조를 강화한다.
- $n \times n$ latent의 이미지를 생성하는 복잡도는 $\mathcal{O}(n^4)$로 상당히 감소한다. 이러한 효율성 향상은 각 $r_k$에서의 병렬적인 토큰 생성으로 인해 발생한다.
Tokenization
저자들은 $K$개의 discrete한 멀티스케일 token map $R = (r_1, \ldots, r_K)$으로 이미지를 인코딩하기 위해 새로운 멀티스케일 quantization 오토인코더를 개발하였다. VQGAN과 동일한 아키텍처를 사용하지만 수정된 멀티스케일 quantization layer를 사용한다.

Residual-style 디자인을 사용한 $f$ 또는 $\hat{f}$에 대한 인코딩 및 디코딩 절차는 Algorithm 1과 2에 자세히 설명되어 있다. 이 residual-style 디자인은 독립적인 interpolation보다 더 나은 성능을 낼 수 있다.
모든 scale에서 공유 codebook $Z$가 사용되어 각 $r_k$의 토큰이 동일한 vocabulary에 속하도록 한다. $z_k$를 $h_K \times w_K$로 업스케일링할 때 발생하는 정보 손실을 해결하기 위해 $K$개의 추가 convolution layer \(\{\phi_k\}_{k=1}^K\)를 사용한다. $f$를 $h_k \times w_k$로 다운샘플링한 후에는 convolution을 사용하지 않는다.
Experiments
1. State-of-the-art image generation
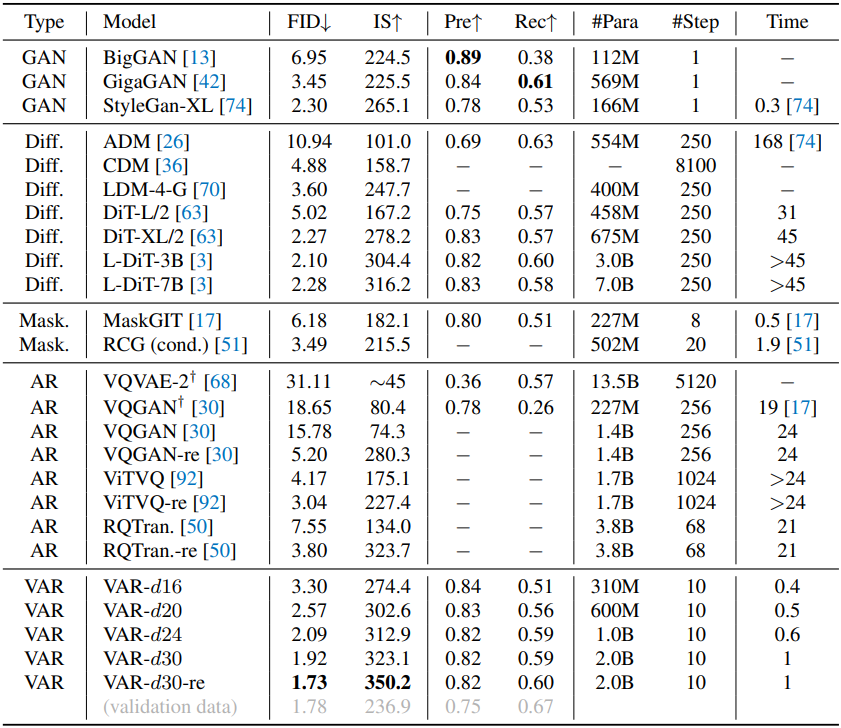
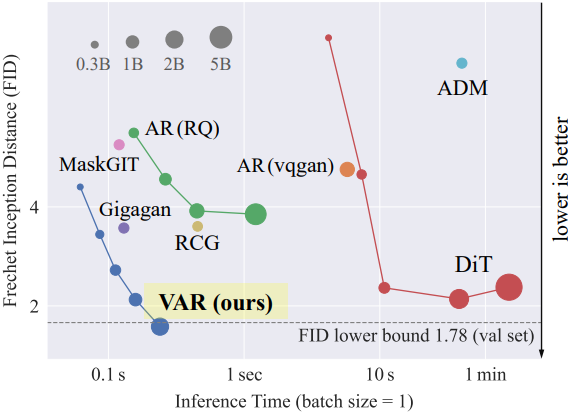
다음은 다른 방법들과 ImageNet 256$\times$256 생성 결과를 비교한 것이다.
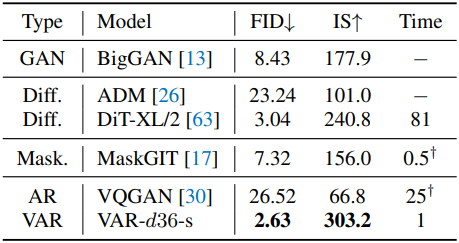
다음은 다른 방법들과 ImageNet 512$\times$512 생성 결과를 비교한 표이다.
2. Power-law scaling laws
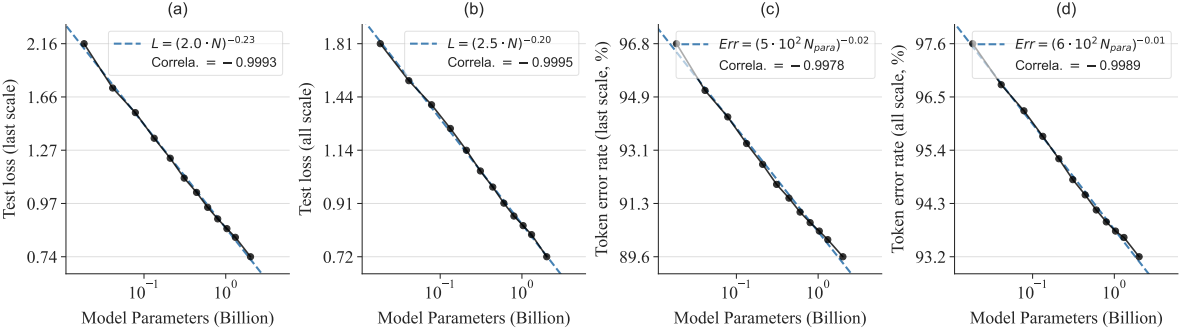
다음은 VAR transformer의 크기에 따른 scaling law들을 나타낸 그래프이다.
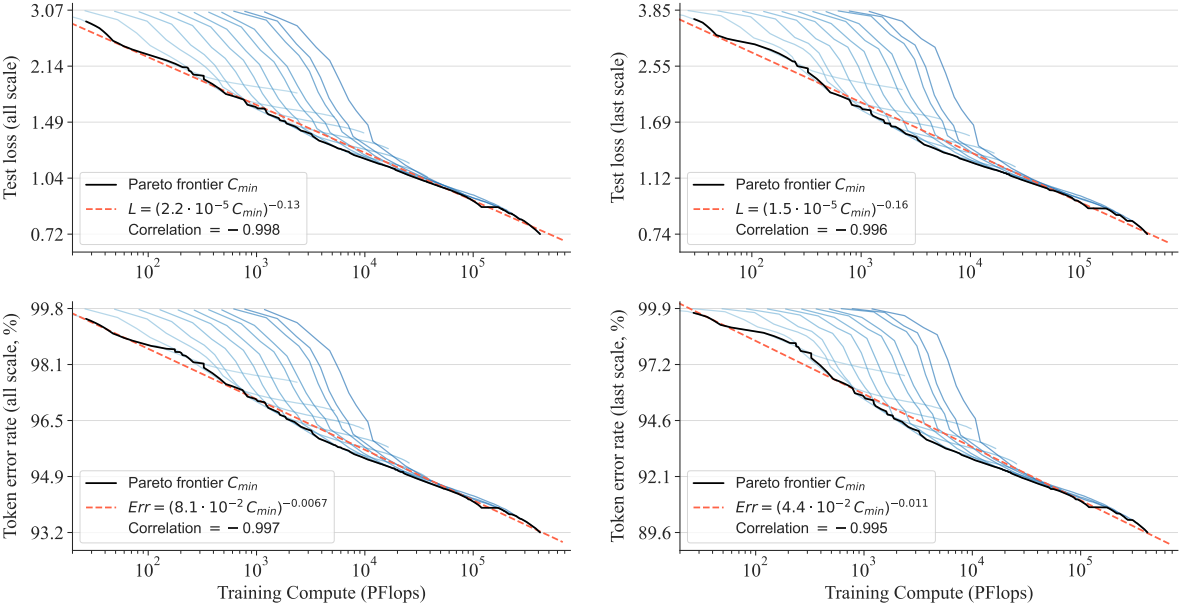
다음은 최적의 학습 연산량에 따른 scaling law들을 나타낸 그래프이다.
3. Visualization of scaling effect
다음은 모델 크기와 학습 연산량에 따른 생성 결과를 비교한 것이다.

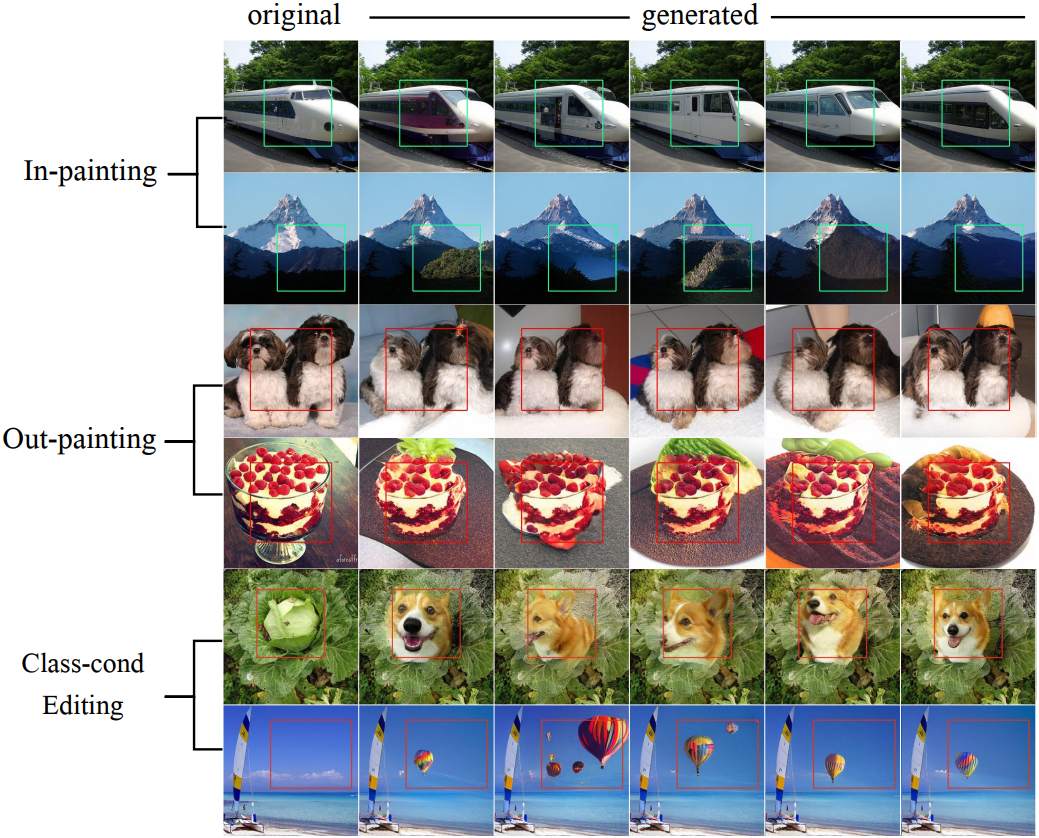
4. Zero-shot task generalization
다음은 downstream task에 대한 zero-shot 생성 결과들이다.
5. Ablation Study
다음은 ablation study 결과이다.