[논문리뷰] UniFormerV2: Spatiotemporal Learning by Arming Image ViTs with Video UniFormer
ICCV 2023. [Paper] [Github]
Kunchang Li, Yali Wang, Yinan He, Yizhuo Li, Yi Wang, Limin Wang, Yu Qiao
Chinese Academy of Sciences | University of Chinese Academy of Sciences | Shanghai AI Laboratory | The University of Hong Kong | Nanjing University
17 Nov 2022
Introduction
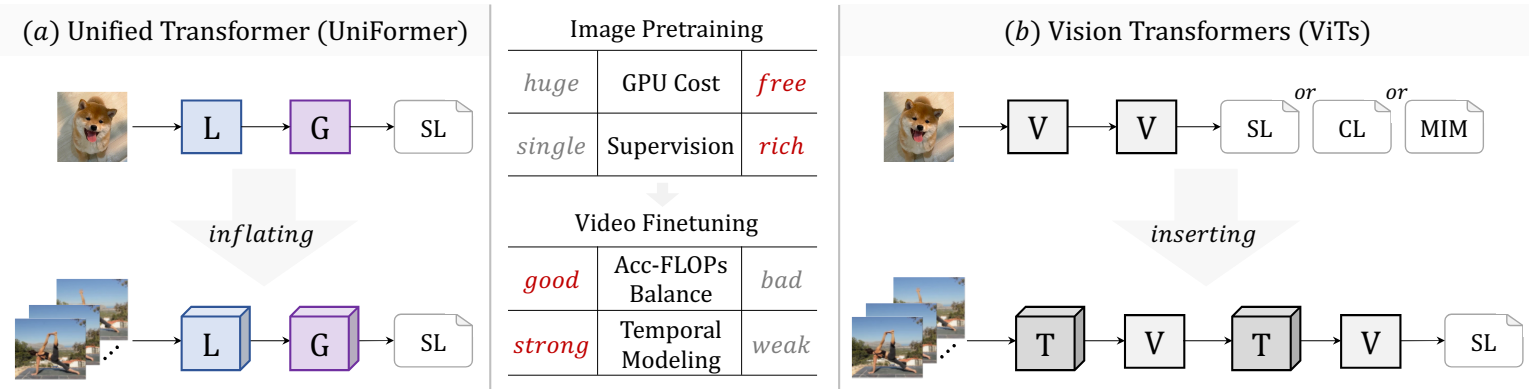
시공간 표현 학습은 동영상 이해의 기본 task이다. 최근 ViT는 이미지 도메인에서 놀라운 성공을 거두었다. 따라서 연구자들은 Multi-Head Self-Attention (MHSA)를 시간적 차원으로 확장하여 동영상 모델링을 위한 이미지 기반 ViT를 전송하기 위해 많은 노력을 기울였다. 그러나 이러한 접근 방식의 시공간 attention 메커니즘은 주로 글로벌 동영상 의존성을 캡처하는 데 초점을 맞추는 반면 로컬 동영상 중복성을 처리할 수 있는 능력은 부족하다. 결과적으로 이러한 모델은 얕은 레이어에서 로컬 동영상 표현을 인코딩하는 데 큰 계산 부담을 지니므로 시공간 학습에서 정확도-효율 균형이 만족스럽지 않다.
이러한 문제를 해결하기 위해 연구자들은 transformer 방식으로 convolution과 self-attention을 Multi-Head Relation Aggregator (MHRA)로 통합하는 간결한 UniFormer를 도입했다. 얕은 레이어과 깊은 레이어에서 각각 로컬 관계와 글로벌 관계를 모델링함으로써 판별적인 시공간 표현을 학습할 수 있을 뿐만 아니라 계산 부담을 크게 줄일 수 있다. 그러나 동영상 모델링을 위한 새로운 아키텍처인 UniFormer는 이미지 기반 사전 학습을 시작으로 하지 않는다. 강력한 시각적 표현을 얻으려면 동영상을 fine-tuning하기 전에 처음부터 이미지를 학습하여 지루한 supervised 사전 학습 단계를 거쳐야 한다. 또한 이미지-텍스트 contrastive learning이나 mask image modeling과 같은 풍부한 supervision 하에 거대한 웹 데이터셋에 대해 잘 사전 학습된 다양한 ViT가 있다. 이러한 모델은 다양한 비전 task에 대해 뛰어난 일반화 능력을 보여준다. 따라서 저자들은 다음과 같은 자연스러운 질문을 하였다.
동영상 모델링을 위해 ViT와 UniFormer의 장점을 모두 통합할 수 있을까?
본 논문에서는 이미지로 사전 학습된 ViT를 UniFormer의 효율적인 동영상 디자인으로 무장함으로써 강력한 동영상 네트워크를 구축하기 위한 일반적인 패러다임을 제안한다. 결과 모델을 UniFormerV2라고 부른다. UniFormer의 간결한 스타일을 계승했지만 로컬 UniBlock들과 글로벌 UniBlock들에 새로운 MHRA를 장착했기 때문이다. 로컬 UniBlock에서는 공간적 ViT 블록 앞에 로컬한 시간적 MHRA를 유연하게 삽입한다. 이 경우 로컬한 시공간 표현을 효과적으로 학습하기 위해 시간적 중복성을 크게 줄이고 사전 학습된 ViT 블록을 활용할 수 있다. 글로벌 UniBlock에서는 query 기반 cross MHRA를 도입한다. 원래 UniFormer의 비용이 많이 드는 글로벌 MHRA와 달리 cross MHRA는 글로벌한 시공간 표현을 효율적으로 학습하기 위해 모든 시공간 토큰을 동영상 토큰으로 요약할 수 있다. 마지막으로 로컬 UniBlock들과 글로벌 UniBlock들을 다단계 융합 아키텍처로 재구성한다. 멀티스케일 시공간 표현을 적응적으로 통합하여 동영상의 복잡한 역학을 캡처할 수 있다.
Method
Overall Framework
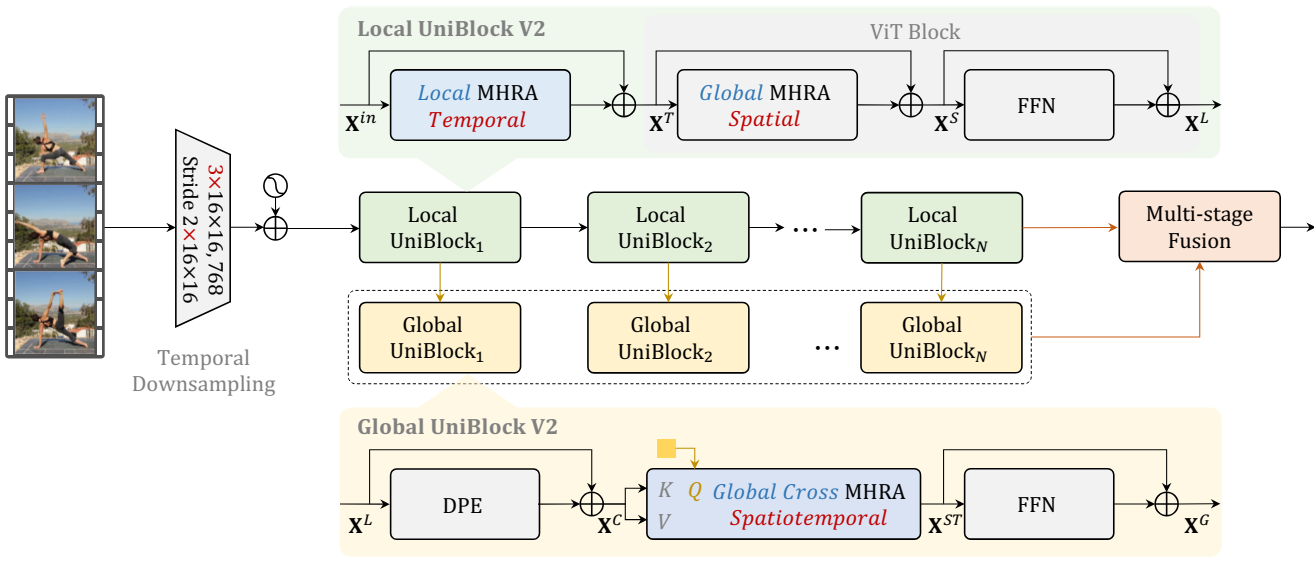
본 논문은 UniFormer의 동영상 디자인으로 이미지 ViT를 무장한 UniFormerV2를 제안하였다. 한편으로는 잘 사전 학습된 ViT의 공간 상호 작용을 완전히 활용하고 보존하여 공간 모델링을 향상시킬 수 있다. 다른 한편으로는 효율적인 UniFormer의 계층적 시간적 상호 작용은 시간적 모델링을 향상시키기 위해 유연하게 채택될 수 있다. 전체 아키텍처는 위 그림에 나와 있다. 먼저 입력 동영상을 토큰으로 project한 다음 로컬 모델링과 글로벌 모델링을 해당 UniBlocks에 의해 수행한다. 마지막으로 다단계 융합 블록은 다양한 단계의 글로벌 토큰을 적응적으로 통합하여 동영상 표현을 더욱 향상시킨다.
구체적으로, 먼저 3D convolution (즉, 3$\times$16$\times$16)을 사용하여 입력 동영상을 $L$개의 시공간 토큰 $X^\textrm{in} \in \mathbb{R}^{L \times C}$로 project한다. 여기서 $L = T \times H \times W$이며, $T$, $H$, $W$는 각각 시간, 높이, 너비를 나타낸다. 원래 ViT 디자인에 따라 16배로 공간 다운샘플링을 수행한다. 더 나은 시간 모델링을 위해 2배로 시간 다운샘플링을 수행한다. 다음으로 로컬 UniBlock들과 글로벌 UniBlock들을 구성한다. 로컬 블록의 경우 로컬한 시간적 MHRA를 삽입하여 이미지로 사전 학습된 ViT 블록을 재구성한다. 이 경우 ViT의 강력한 공간 표현을 효과적으로 활용할 수 있을 뿐만 아니라 로컬한 시간적 중복성을 효율적으로 줄일 수 있다. 또한 전체 시공간 의존성을 캡처할 수 있는 각 로컬 UniBlock 위에 글로벌 UniBlock을 도입한다. 컴퓨팅 효율성을 위해 모든 시공간 토큰을 글로벌 동영상 토큰으로 집계하는 query 기반 cross MHRA를 설계한다. 여러 단계에서 서로 다른 수준의 글로벌 semantic을 가진 이러한 모든 토큰은 판별적인 동영상 표현을 위해 더욱 융합된다.
1. Local UniBlock
잘 학습된 공간 표현에 대한 시간 의존성을 효율적으로 모델링하기 위해 표준 ViT 블록 앞에 로컬한 시간적 MHRA를 삽입하여 새로운 로컬 UniBlock을 만든다.
\[\begin{aligned} X^T &= \textrm{LT_MHRA} (\textrm{Norm} (X^\textrm{in})) + X^\textrm{in} \\ X^S &= \textrm{GS_MHRA} (\textrm{Norm} (X^T)) + X^T \\ X^L &= \textrm{FFN} (\textrm{Norm} (X^S)) + X^S \end{aligned}\]$\textrm{LT_MHRA}$와 $\textrm{GS_MHRA}$는 각각 local temporal MHRA와 global spatial MHRA이다. $\textrm{FFN}$은 GeLU로 구분되는 2개의 linear projection으로 구성된다. 또한 UniFormer의 정규화를 따라, Batch Norm (BN)을 로컬 MHRA 이전에 적용하고 Layer Norm (LN)을 글로벌 MHRA와 FFN 이전에 적용한다. $\textrm{GS_MHRA}$와 $\textrm{FFN}$은 이미지로 사전 학습된 ViT 블록에서 온다. 일반적으로 MHRA는 multi-head fusion을 통해 토큰 관계를 학습한다.
\[\begin{aligned} R_n (X) &= A_n V_n (X) \\ \textrm{MHRA} (X) &= \textrm{Concat} (R_1 (X); R_2 (X); \cdots; R_N (X)) U \end{aligned}\]여기서 $R_n (\cdot)$은 $n$번째 head의 relation aggregator이다. $A_n$은 토큰 관계를 설명하는 affinity matrix이고 $V_n (\cdot)$은 linear projection이며, $U \in \mathbb{R}^{C \times C}$는 학습 가능한 fusion matrix이다. 로컬 UniBlock의 경우 $\textrm{LT_MHRA}$를 삽입하여 원래 UniFormer와 유사한 디자인 통찰력을 공유하는 로컬한 시간적 중복을 줄인다. 따라서 $\textrm{LT_MHRA}$의 affinity는 시간적 튜브 $t \times 1 \times 1$에서 학습 가능한 파라미터 행렬 $a_n \in \mathbb{R}^{t \times 1 \times 1}$과 함께 로컬이다.
\[\begin{equation} A_n^\textrm{LT} (X_i, X_j) = a_n^{i-j}, \quad \textrm{where} \quad j \in \Omega_i^{t \times 1 \times 1} \end{equation}\]이를 통해 튜브에서 하나의 토큰 $X_i$와 다른 토큰 $X_j$ 사이의 로컬한 시간 관계를 효율적으로 학습할 수 있다. 또는 $\textrm{GS_MHRA}$는 원래 ViT 블록에 속한다. 따라서 \(\textrm{GS_MHRA}\)에서 affinity는 단일 프레임 $1 \times H \times W$에서 글로벌한 공간적 self-attention을 의미한다.
\[\begin{equation} A_n^\textrm{GS} (X_i, X_j) = \frac{\exp \{ Q_n (X_i)^\top K_n (X_j) \}}{ \sum_{j' \in \Omega_{1 \times H \times W}} \exp \{ Q_n (X_i)^\top K_n (X_{j'}) \}} \end{equation}\]여기서 $Q_n (\cdot), K_n (\cdot) \in \mathbb{R}^{L \times \frac{C}{N}}$은 $n$번째 head의 서로 다른 linear projection이다.
Discussion
- 로컬 UniBlock의 시공간적 affinity는 $A_n^\textrm{LT}$와 $A_n^\textrm{GS}$로 분해할 수 있다. 이를 통해 UniFormer의 효율적인 동영상 처리 디자인을 활용할 수 있을뿐만 아니라 효과적인 이미지 ViT를 상속할 수 있게 된다. 원래 UniFormer의 이러한 로컬 affinity는 공동으로 시공간적이다. 파라미터 행렬은 처음부터 학습해야 하므로 필연적으로 학습 비용이 증가한다.
- ViT 블록의 위치 인코딩이 토큰 위치를 특성화했기 때문에 UniFormer와 비교할 때 로컬 UniBlock의 Dynamic Position Encoding (DPE)를 포기한다.
- TimeSformer에서와 같이 글로벌 시간 모델링을 적용하는 대신 시간 특성화에 로컬 affinity를 사용하여 UniFormer 스타일에서 시간 중복을 처리하여 계산 부담을 크게 줄인다.
2. Global UniBlock
명시적으로 시공간적 스케일에서 장거리 의존성 모델링을 수행하기 위해 UniFormerV2에 글로벌 UniBlock을 도입한다. 구체적으로 이 글로벌 UniBlock은 다음과 같이 DPE, MHRA, FFN의 세 가지 기본 구성 요소로 구성된다.
\[\begin{aligned} X^C &= \textrm{DPE} (X^L) + X^L \\ X^\textrm{ST} &= \textrm{C_MHRA} (\textrm{Norm} (q), \textrm{Norm} (X^C)) \\ X^G &= \textrm{FFN} (\textrm{Norm} (X^\textrm{ST})) + X^\textrm{ST} \end{aligned}\]DPE는 시공간적 depth-wise convolution으로 인스턴스화된다. 동영상 표현을 효율적으로 구성하기 위해 cross-attention 스타일로 $\textrm{C_MHRA}$를 설계한다.
\[\begin{aligned} R_n^C (q, X) &= A_n^C (q, X) V_n (X) \\ \textrm{C_MHRA} (q, X) &= \textrm{Concat} (R_1^C (q, X); R_2^C (q, X); \cdots; R_N^C (q, X)) U \end{aligned}\]여기서 $R_n^C (q, \cdot)$는 cross relation aggregator이며, 학습 가능한 query $q \in \mathbb{R}^{1 \times C}$를 이 query $q$와 모든 시공간 토큰 $X$ 사이의 모델링 의존성을 통해 동영상 표현으로 변환할 수 있다. 먼저 cross affinity matrix $A_n^C (q, X)$를 계산하여 $q$와 $X$ 사이의 관계를 학습한다.
\[\begin{equation} A_n^C (q, X_j) = \frac{\exp \{ Q_n (q)^\top K_n (X_j) \}}{ \sum_{j' \in \Omega_{T \times H \times W}} \exp \{ Q_n (q)^\top K_n (X_{j'}) \}} \end{equation}\]그런 다음 linear projection을 사용하여 $X$를 시공간 컨텍스트 $V_n (X)$로 변환한다. 그 후, affinity $A_n^C (q, X)$의 guidance에 따라 이러한 컨텍스트 $V_n (X)$를 학습 가능한 쿼리로 집계한다. 마지막으로, 모든 head의 향상된 query 토큰은 linear projection $U \in \mathbb{R}^{C \times C}$에 의해 최종 동영상 표현으로 추가 융합된다. Query 토큰은 안정적인 학습을 위해 0으로 초기화된다.
Discussion
- 로컬 UniBlock 위에 글로벌 UniBlock을 추가하여 토큰 형태로 멀티스케일 시공간 표현을 추출한다. 이러한 디자인은 사전 학습된 아키텍처를 손상시키지 않으면서 판별적인 동영상 표현을 강화하는 데 도움이 된다.
- 전형적인 글로벌 시공간 attention은 2차 복잡도로 인해 계산적으로 무겁다. 더 나은 정확도-계산 균형을 추구하기 위해 UniFormerV2에서 글로벌 MHRA의 cross-attention 스타일을 도입하여 $O(L^2)$에서 $O(L)$까지 계산 복잡도를 크게 줄인다. 여기서 $L$은 토큰 수이다. 더 중요한 것은 query $q$가 학습 가능하기 때문에 모든 $L$개의 토큰의 시공간 컨텍스트를 적응적으로 통합하여 동영상 인식을 높일 수 있다는 것이다.
- 글로벌 UniBlock은 UniFormer의 DPE 디자인을 계승한다.
3. Multi-Stage Fusion Block
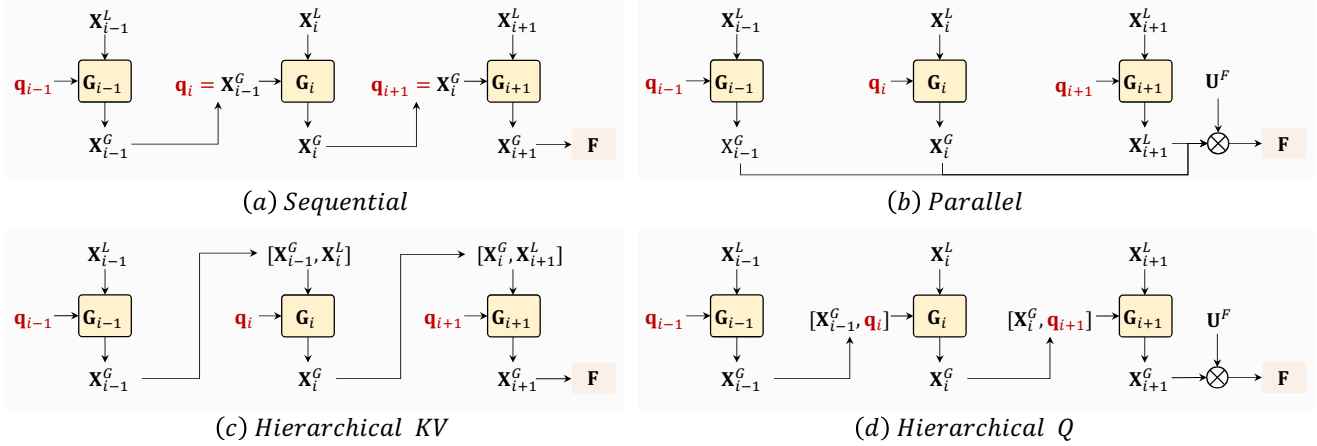
본 논문은 위 그림과 같이 각 글로벌 UniBlock의 모든 동영상 토큰을 통합하는 다단계 융합 블록을 제안한다. 단순화를 위해 $i$번째 글로벌 블록을 $X_i^G = G_i (q_i, X_i^L)$로 표시한다. 로컬 UniBlock의 토큰 $X_i^L$가 주어지면 글로벌 블록은 학습 가능한 query $q$를 동영상 토큰 $X_i^G$로 변환한다. 본 논문에서는 모든 글로벌 블록 \(\{ X_i^G \}_{i=1}^N\)의 동영상 토큰을 최종 동영상 표현 $F$로 통합하기 위한 4가지 융합 전략을 탐색하고, 효율성과 효율성 측면에서 융합을 수행하기 위해 순차적인 방식을 사용한다.
연구된 융합 방식은 다음과 같다.
- 순차적인 방식: $X_i^G = G_i (X_{i-1}^G, X_i^L)$
- 병렬 방식: $F = \textrm{Concat} (X_1^G, \ldots, X_N^G) U^F$
- 계층적 KV 방식: $X_i^G = G_i (q_i, [X_{i-1}^G, X_i^L])$
- 계층적 Q 방식: $X_i^G = G_i ([X_{i-1}^G, q_i], X_i^L)$
마지막으로 로컬 블록과 글로벌 블록의 최종 토큰을 동적으로 통합하여 인식 성능을 효과적으로 촉진한다. 구체적으로 최종 로컬 UniBlock에서 클래스 토큰 $F^C$를 추출하고 가중 합으로 동영상 토큰 $F$와 함께 추가한다.
\[\begin{equation} Z = \alpha F + (1 - \alpha) F^C \end{equation}\]여기서 $\alpha$는 시그모이드 함수로 처리되는 학습 가능한 파라미터이다.
Experiments
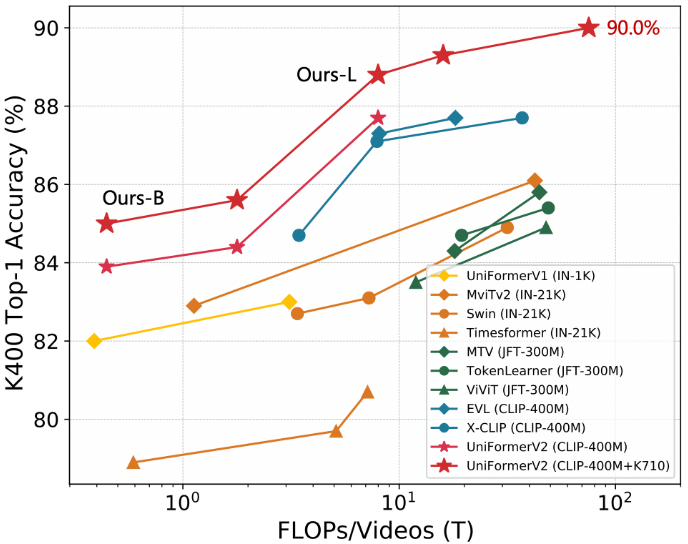
1. Comparison to state-of-the-art
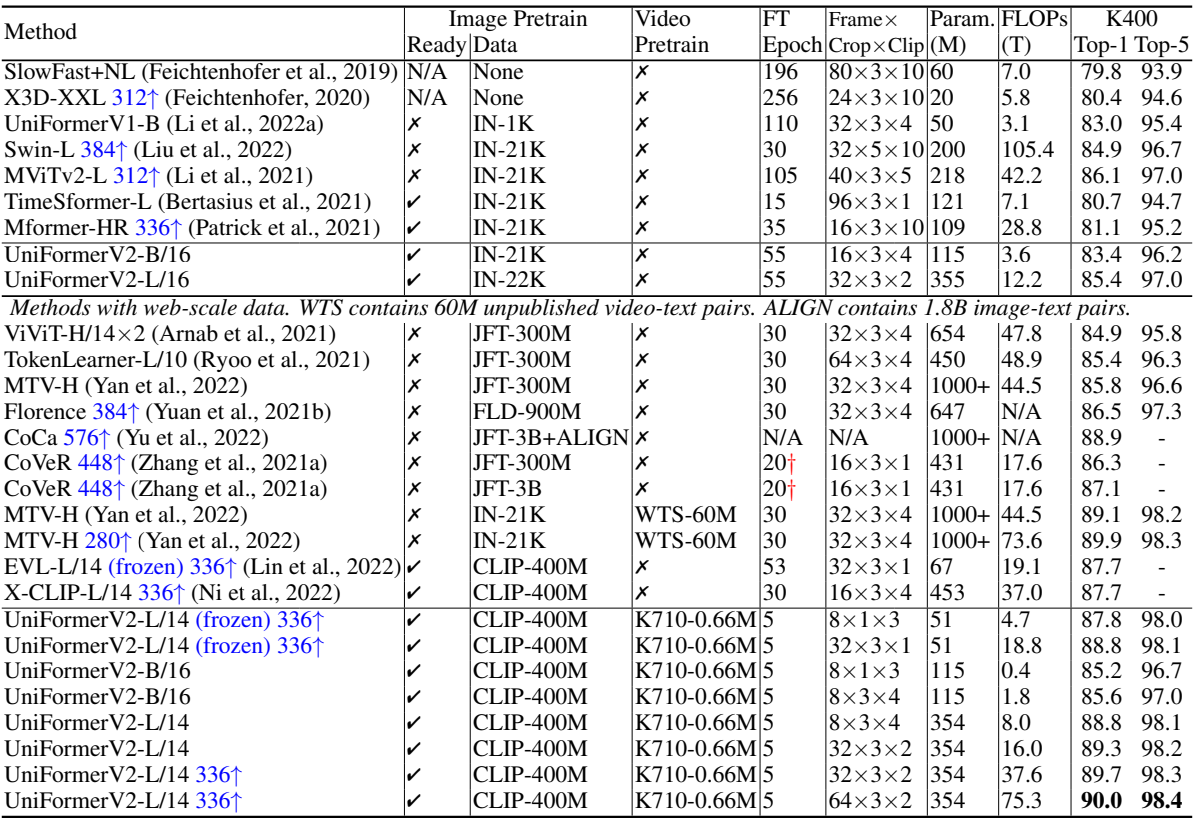
다음은 Kinetics-400에서 SOTA와 비교한 결과이다.
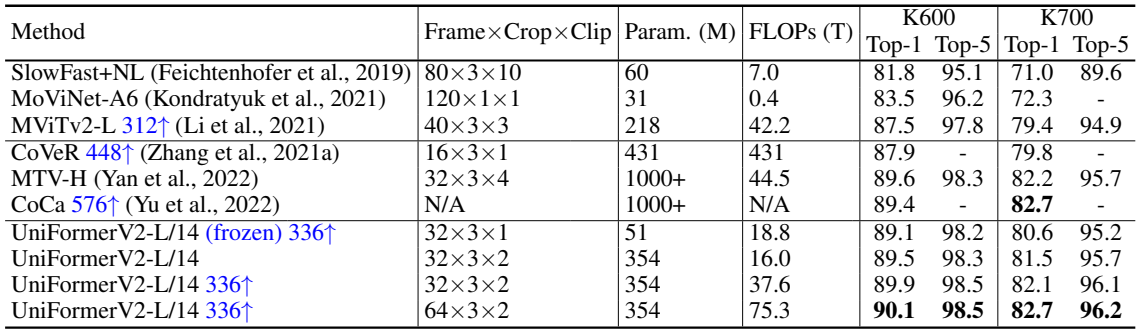
다음은 Kinetics-600/700에서 SOTA와 비교한 결과이다.
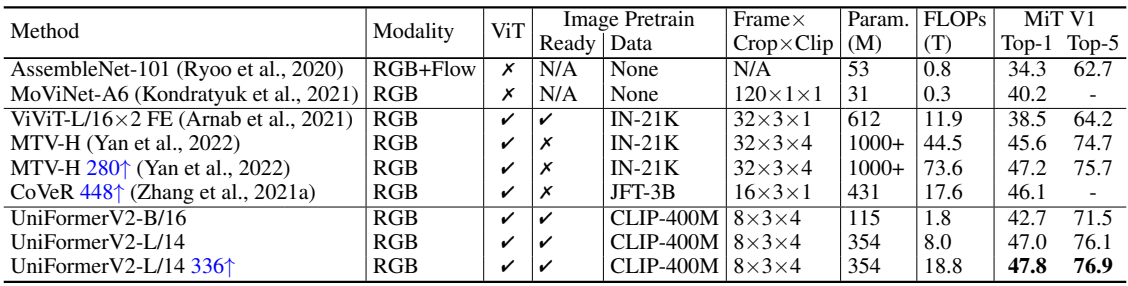
다음은 Moments in Time V1에서 SOTA와 비교한 결과이다.
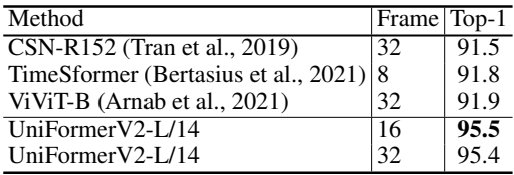
다음은 Something-Something V2에서 SOTA와 비교한 결과이다.
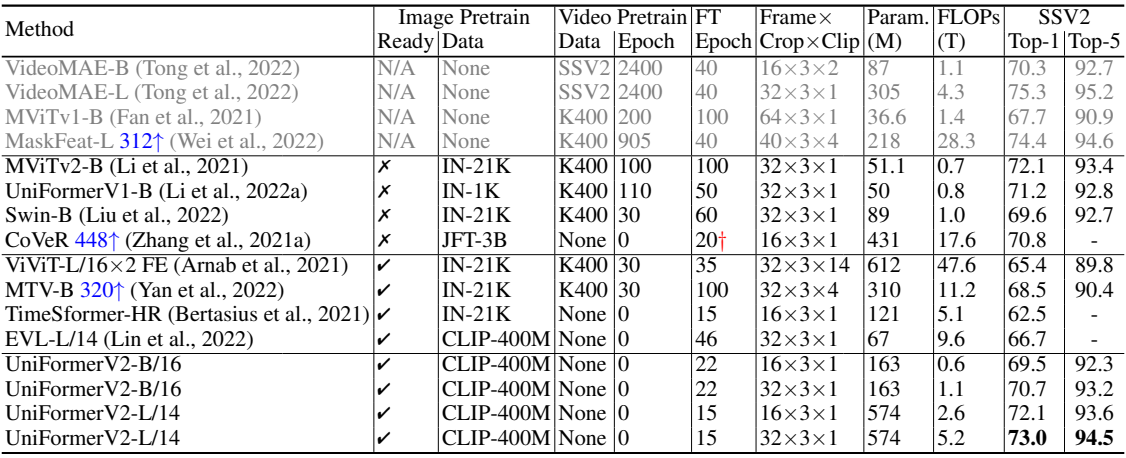
다음은 Something-Something V1에서의 결과이다.
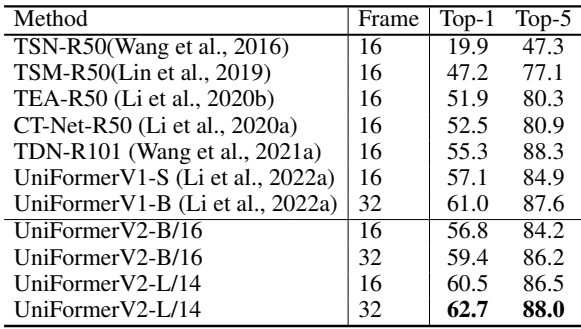
다음은 ActivityNet에서의 결과이다.
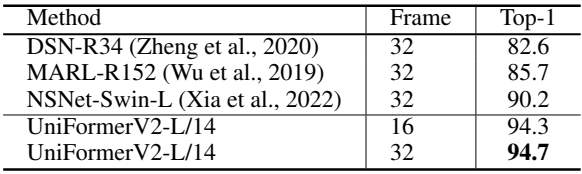
다음은 HACS에서의 결과이다.
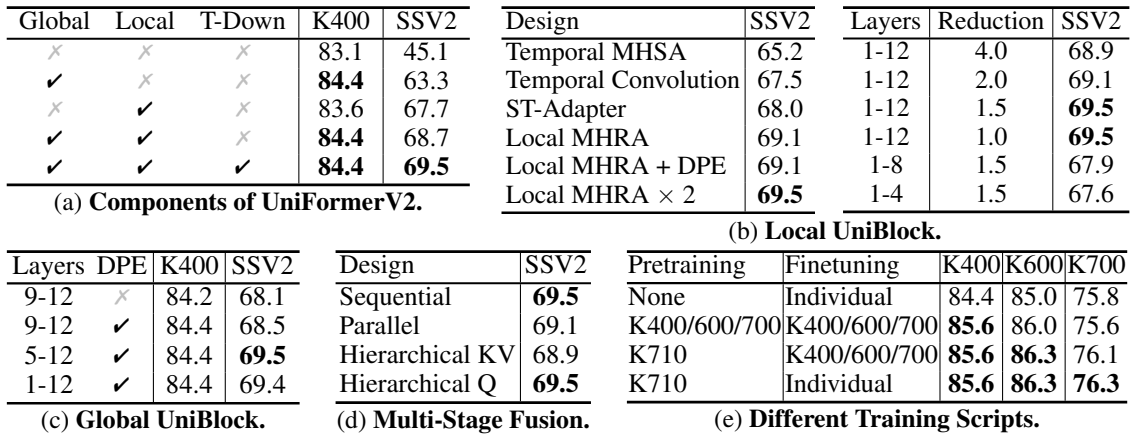
2. Ablation Studies
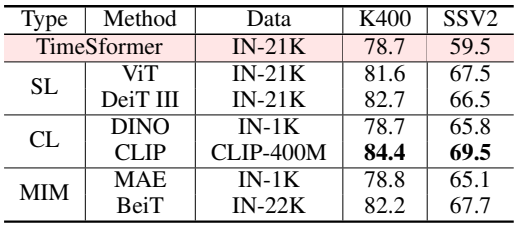
다음은 다양한 사전 학습된 ViT들에 대한 결과이다.
다음은 ablation study 결과이다.