[논문리뷰] One Transformer Fits All Distributions in Multi-Modal Diffusion at Scale (UniDiffuser)

ICML 2023. [Paper] [Github]
Fan Bao, Shen Nie, Kaiwen Xue, Chongxuan Li, Shi Pu, Yaole Wang, Gang Yue, Yue Cao, Hang Su, Jun Zhu
Tsinghua University | ShengShu | Renmin University of China | Beijing Academy of AI | Pazhou Laboratory
12 Mar 2023

Introduction

최근 우리는 멀티모달 데이터에 대한 생성 모델링의 급속한 발전으로 인해 콘텐츠 제작 혁명을 목격하고 있다. 특히 diffusion model은 내용이 입력 텍스트 조건과 잘 일치하는 고충실도의 다양한 데이터를 생성하는 놀라운 능력을 보여주었다.

그러나 이러한 생성 모델은 하나의 task만 허용하는 맞춤형 시스템으로 설계되었다. 실제로 인간은 임의의 컨디셔닝 타입을 사용하여 다양한 멀티모달 콘텐츠를 동시에 생성할 수 있다. 예를 들어, 멀티모달 데이터에 대한 일반적인 생성 시스템을 향하여 모든 타입의 멀티모달 생성 task를 다룰 수 있는 통합 학습 프레임워크는 기본 구성 요소 중 하나이다.

이 task는 확률적 모델링의 관점에서 해당 분포를 맞추면 해결된다. 예를 들어, text-to-image 생성은 조건부 분포 $p(\textrm{Image} \vert \textrm{Text})$를 학습하는 것으로 공식화할 수 있다. 모든 관련 분포를 맞추는 고전적인 방법은 암시적이다. 먼저 결합 분포를 학습한 다음 추가 절차를 통해 주변 분포와 조건부 분포를 추론한다. 이는 대규모 멀티모달 데이터에서는 감당할 수 없다.

대조적으로, 본 논문은 추가 학습 또는 inference 오버헤드를 도입하지 않고 하나의 모델에서 모든 관련 분포를 명시적으로 맞추는 diffusion 기반 프레임워크인 UniDiffuser를 제시한다. 본 논문의 핵심 통찰력은 모든 분포에 대한 diffusion model을 학습하는 것은 섭동 레벨 (즉, timestep)이 다른 modality에 따라 다를 수 있는 섭동 데이터의 noise를 예측하는 것으로 통합될 수 있다. 예를 들어, 0 레벨은 해당 modality가 주어진 조건부 생성을 나타내고, 최대 레벨은 해당 modality를 무시하여 unconditional한 다른 modality 생성을 나타낸다.

UniDiffuser는 원래 diffusion model에 대한 최소한의 수정으로 동시에 모든 분포를 학습한다. 즉, 단일 modality 대신 모든 modality의 데이터를 섭동시키고, 서로 다른 modality의 개별 timestep을 입력하고, 단일 modality 대신 모든 modality의 noise 예측한다. 당연히 UniDiffuser는 맞춤형 diffusion model과 동일한 방식으로 모든 종류의 생성을 수행할 수 있다. 또한 UniDiffuser는 이미 주변 분포를 모델링하기 때문에 조건부 생성과 공동 생성 모두에서 샘플 품질을 개선하기 위해 무료로 classifier-free guidance를 수행할 수 있다.

확률적 모델링 프레임워크 외에도 다양한 modality의 입력 유형을 처리할 수 있는 통합 아키텍처는 일반 생성 시스템의 또 다른 기본 구성 요소이다. 특히 Transformer의 출현과 생성 모델링에 대한 애플리케이션은 modality 간의 상호 작용을 캡처할 수 있는 유망한 솔루션을 제공한다. 당연히 UniDiffuser는 transformer 기반 backbone을 사용한다.

저자들은 대규모 이미지-텍스트 데이터의 이미지용 CLIP 인코더와 텍스트용 GPT-2 디코더를 추가하여 latent space에 UniDiffuser를 구현하였다. UniDiffuser는 추가 오버헤드 없이 적절한 timestep을 설정하여 이미지, 텍스트, text-to-image, image-to-text, 이미지-텍스트 쌍 생성을 수행할 수 있다. 특히 UniDiffuser는 모든 task에서 사실적인 샘플을 생성할 수 있으며 정량적 결과는 기존 범용 모델보다 우수할 뿐만 아니라 대표 task에서 해당 맞춤형 모델과 비슷한 성능을 보인다.

Method

1. UniDiffuser: One Diffusion Fits All Distributions

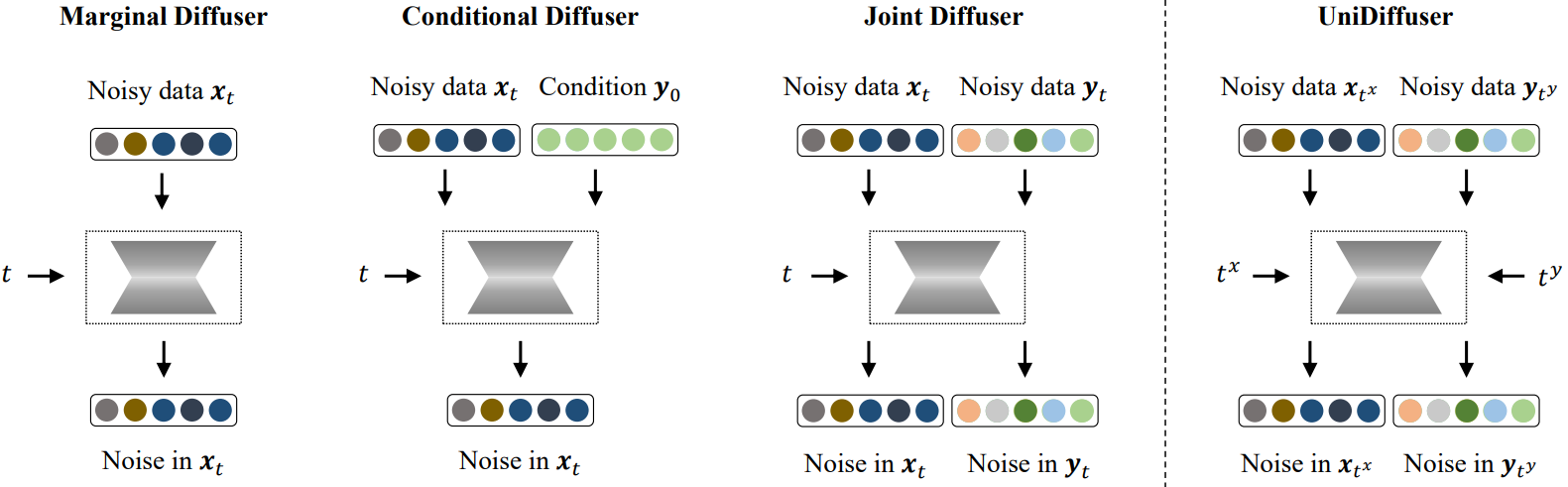
분포 $q(x_0, y_0)$에서 샘플링된 두 가지 데이터 modality가 있다고 가정하자. $q(x_0, y_0)$에 의해 결정되는 모든 관련 분포, 즉 주변 분포 $q(x_0)$와 $q(y_0)$, 조건부 분포 $q(x_0 \vert y_0)$와 $q(y_0 \vert x_0)$, 결합 분포 $q(x_0, y_0)$를 캡처할 수 있는 diffusion 기반 모델을 설계하는 것을 목표로 한다.

Diffusion model로 분포를 학습하는 것은 noise에 대한 조건부 기대값을 추정하는 것과 같다. 특히, 주변 분포 $q(x_0)$를 모델링하는 것은 $x_t$에 주입된 noise의 조건부 기대값, 즉 $\mathbb{E} [\epsilon^x \vert x_t]$를 추정하는 것과 같다. 마찬가지로, 조건부 분포 $q(x_0 \vert y_0)$와 결합 분포 $q(x_0, y_0)$를 모델링할 때 각각 $\mathbb{E} [\epsilon^x \vert x_t, y_0]$와 $\mathbb{E} [\epsilon^x, \epsilon^y \vert x_t, y_t]$를 추정한다.

주요 관찰은 위의 모든 조건부 기대값이 $\mathbb{E} [\epsilon^x, \epsilon^y \vert x_{t^x}, y_{t^y}]$의 일반 형식으로 통합될 수 있다는 것이다. 여기서 $t^x$와 $t^y$는 서로 다를 수 있는 두 개의 timestep이고 $x_{t^x}$와 $y_{t^y}$는 해당 섭동 데이터이다. 특히 최대 timestep $T$는 주변화 (marginalizing)를 의미한다. 즉, $t^y = T$로 설정하면 주변 분포 $q(x_0)$에 해당하는

\[\begin{equation} \mathbb{E} [\epsilon^x \vert x_{t^x}, y_T] \approx \mathbb{E} [\epsilon^x \vert x_{t^x}] \end{equation}\]

을 갖게 된다.

마찬가지로 timestep이 0이라는 것은 해당 modality에 대한 조건을 의미하고 연결된 timestep은 두 가지 modality를 공동으로 샘플링하는 것을 의미한다. $t^y = 0$으로 설정한 $\mathbb{E} [\epsilon^x \vert x_{t^x}, y_0]$는 조건부 분포 $q(x_0 \vert y_0)$에 해당하고, $t^x = t^y = t$로 설정한 $\mathbb{E} [\epsilon^x, \epsilon^y \vert x_t, y_t]$는 결합 분포 $q(x_0, y_0)$에 해당한다. 또한 일반적으로 $\mathbb{E} [\epsilon^x, \epsilon^y \vert x_{t^x}, y_{t^y}]$를 추정하여 모든 $t^y$와 $t^x$에 대해 $q(x_0 \vert y_{t^y})$와 $q(y_0 \vert x_{t^x})$를 특성화하고 noisy한 입력을 조건으로 데이터를 생성할 수 있다.

$q(x_0, y_0)$에 의해 결정되는 모든 관련 분포를 모델링하기 위해 모든 $0 \le t^x , t^y \le T$에 대해 $\mathbb{E} [\epsilon^x, \epsilon^y \vert x_{t^x}, y_{t^y}]$를 학습한다. 구체적으로 DDPM과 유사하게 다음과 같은 regression loss를 최소화하여 $x_{t^x}$와 $y_{t^y}$에 함께 주입되는 noise를 예측하기 위해 공동 noise 예측 네트워크 $\epsilon_\theta (x_{t^x}, y_{t^y}, t^x, t^y)$를 사용한다.

\[\begin{equation} \mathbb{E}_{x_0, y_0, \epsilon^x, \epsilon^y, t^x, t^y} [\| \epsilon_\theta (x_{t^x}, y_{t^y}, t^x, t^y) - [\epsilon^x, \epsilon^y] \|_2^2] \end{equation}\]

여기서 $(x_0, y_0)$는 랜덤 데이터 포인트이고 $[\cdot, \cdot]$은 concatenation이다. $\epsilon^x$와 $\epsilon^y$는 표준 가우시안 분포에서 샘플링되명, $t^x$와 $t^y$는 \(\{1, \ldots, T\}\)에서 균일하게 샘플링된다. 통합된 방식으로 여러 분포를 캡처하기 때문에 이 방법을 UniDiffuser라고 한다.

위의 목적 함수는 원래 DDPM만큼 간단하다. 게다가 단일 파라미터 업데이트의 경우 UniDiffuser는 여러 분포에 대해 한 번의 forward-backward 계산만 필요하므로 원래 DDPM만큼 효율적이다. UniDiffuser의 기울기 추정값은 두 개의 독립적인 timestep으로 인해 원래 DDPM보다 약간 더 높은 분산을 갖지만 UniDiffuser가 더 느린 수렴으로 인해 어려움을 겪는 것은 관찰되지 않는다.

UniDiffuser는 하나의 공동 noise 예측 네트워크로 모든 분포를 맞추려고 시도하므로 backbone이 modality 간의 상호 작용을 처리할 수 있고 대규모 데이터와 여러 task에 맞게 확장 가능해야 한다. 대규모 멀티모달 표현 학습에서 transformer의 뛰어난 성능에 영감을 받아 UniDiffuser에서 transformer 기반 네트워크를 사용한다.

하나의 공동 noise 예측 네트워크가 주어지면 UniDiffuser는 특정 샘플러에 따라 unconditional 샘플링, 조건부 샘플링, joint 샘플링을 수행할 수 있다. 특히 timestep을 적절하게 설정하면 UniDiffuser의 inference 절차는 맞춤형 모델과 동일하다. 이에 비해 멀티모달 데이터에 대한 단일 결합 분포를 학습하려면 주변 분포 또는 조건부 분포에서 샘플링하기 위한 추가 절차 (ex. Markov Chain Monte Carlo)가 필요하며, 이는 대규모 멀티모달 데이터에서 감당할 수 없다.

2. Classifier-Free Guidance for Free

Classifier-free guidance (CFG)는 샘플링 중에 조건부 모델과 unconditional 모델을 선형으로 결합한다. Diffusion model에서 샘플 품질과 이미지-텍스트 정렬을 개선하는 것은 간단하면서도 효과적이다. 특히 CFG는 학습 프로세스를 수정하지 않고 UniDiffuser의 조건부 샘플링과 joint 샘플링에 직접 적용할 수 있다.

$\epsilon_\theta$의 출력을 $\epsilon_\theta^x$와 $\epsilon_\theta^y$의 concatenation으로 표시하자.

\[\begin{equation} \epsilon_\theta = [\epsilon_\theta^x, \epsilon_\theta^y] \end{equation}\]

UniDiffuser는 조건부 모델과 unconditional 모델을 모두 캡처하기 때문에 조건부 샘플링에서 무료로 CFG를 수행할 수 있다. 예를 들어 다음과 같이 $y_0$을 조건으로 $x_0$을 생성할 수 있다.

\[\begin{equation} \hat{\epsilon}_\theta^x (x_t, y_0, t) = (1 + s) \epsilon_\theta^x (x_t, y_0, t, 0) - s \epsilon_\theta^x (x_t, \epsilon^y, t, T) \end{equation}\]

여기서 $\epsilon_\theta^x (x_t, y_0, t, 0)$와 $\epsilon_\theta^x (x_t, \epsilon^y, t, T)$는 각각 조건부 모델과 unconditional 모델이며, $s$는 guidance scale이다. 원래 CFG와 달리 UniDiffuser는 파라미터 공유를 위해 null 토큰을 지정할 필요가 없다.

CFG는 joint 샘플링에도 적용할 수 있다. $t^x = t^y = t$로 설정하면 joint score model은 다음과 같이 조건부 모델의 형태로 동등하게 표현될 수 있다.

\[\begin{aligned} \epsilon_\theta (x_t, y_t, t, t) &\approx - \sqrt{\vphantom{1} \bar{\beta}_t} [\nabla_{x_t} \log q(x_t, y_t), \nabla_{y_t} \log q(x_t, y_t)] \\ &= - \sqrt{\vphantom{1} \bar{\beta}_t} [\nabla_{x_t} \log q(x_t \vert y_t), \nabla_{y_t} \log q(y_t \vert x_t)] \end{aligned}\]

여기서 $q(x_t, y_t)$는 동일한 noise 레벨 $t$에서 섭동된 데이터의 결합 분포이다. Score function 간의 위 관계에서 영감을 얻은 $\epsilon_\theta (x_t, y_t, t, t)$는 한 쌍의 조건부 score $\nabla_{x_t} \log q(x_t \vert y_t)$와 $\nabla_{y_t} \log q(x_t \vert y_t)$를 근사하는 것으로 볼 수 있다. CFG와 동일한 정신으로 다음과 같이 결합 모델을 해당 unconditional 모델로 보간하여 각 조건부 score를 대체할 수 있다.

\[\begin{aligned} \hat{\epsilon}_\theta (x_t, y_t, t) &= (1 + s) \epsilon_\theta (x_t, y_t, t, t) - s [\epsilon_\theta^x (x_t, \epsilon^y, t, T), \epsilon_\theta^y (\epsilon^x, y_t, T, t)] \\ &\approx - \sqrt{\vphantom{1} \bar{\beta}_t} [(1 + s) \nabla_{x_t} \log q (x_t \vert y_t) - s \nabla_{x_t} \log q (x_t), \\ & \; \qquad \qquad (1 + s) \nabla_{y_t} \log q (y_t \vert x_t) - s \nabla_{y_t} \log q (y_t)] \end{aligned}\]

여기서 $\epsilon_\theta^x (x_t, \epsilon^y, t, T)$와 $\epsilon_\theta^y (\epsilon^x, y_t, T, t)$는 unconditional 모델을 나타낸다.

UniDiffuser on Images and Texts

이미지와 텍스트는 일상 생활에서 가장 흔한 modality이다. 따라서 두 modality에 대한 UniDiffuser의 유효성을 검증하는 것이 대표적이다.

구현은 2단계로 이루어진다.

1. 이미지와 텍스트를 이미지 인코더와 텍스트 인코더를 통해 연속적인 latent 임베딩 $x_0$와 $y_0$으로 변환하고 재구성을 위한 두 개의 디코더를 도입한다.
2. Latent 임베딩 $x_0$와 $y_0$에서 transformer로 parameterize된 UniDiffuser를 학습시킨다.

1. Encoding Images and Texts into Latent Space

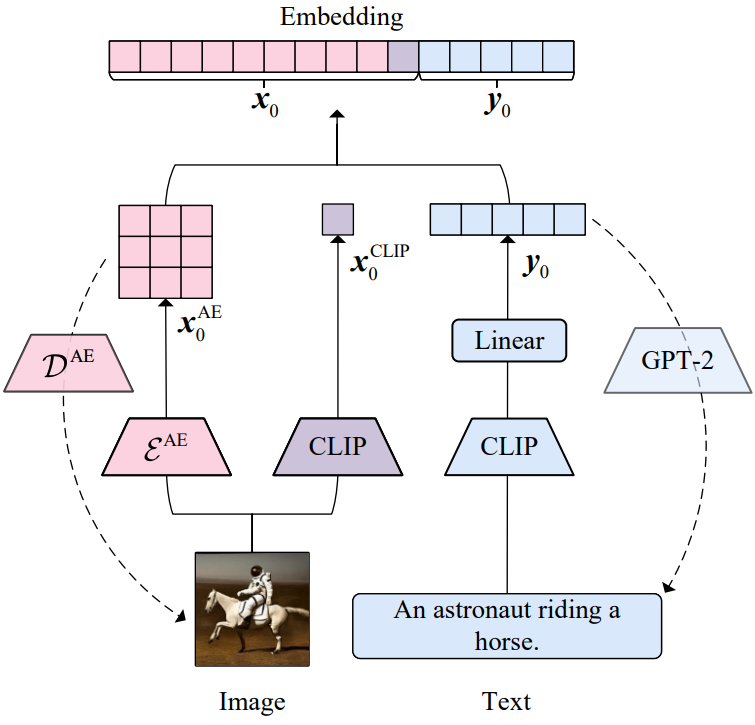
이미지 및 텍스트 인코더-디코더는 위 그림에 나와 있다.

이미지 인코더-디코더

이미지 인코더는 두 부분으로 구성된다. 첫 번째 부분은 Stable Diffusion에 사용되는 이미지 오토인코더이다. 인코더 $\mathcal{E}^\textrm{AE}$를 사용하여 이미지 재구성 $x_0^\textrm{AE}$에 대한 임베딩을 얻는다. 두 번째 부분은 이미지 CLIP (ViT-B/32)이다. 512차원의 semantic 임베딩 $x_0^\textrm{CLIP}$을 추출한다. 이미지에 대한 최종 latent 임베딩은 두 부분의 출력을 concat하는 것이다.

\[\begin{equation} x_0 = [x_0^\textrm{AE}, x_0^\textrm{CLIP}] \end{equation}\]

경험적으로 $x_0^\textrm{AE}$는 Stable Diffusion에서 이미지 디코더 $\mathcal{D}^{AE}$를 통한 이미지 재구성에 충분하고 추가 $x_0^\textrm{CLIP}$은 이미지-텍스트 생성에서 이미지의 semantic을 이해하는 데 도움이 된다. 저자들은 두 임베딩의 서로 다른 역할이 본질적으로 원래의 목적 함수들에 의해 발생한다고 가정하였다.

텍스트 인코더-디코더

텍스트 인코더는 Stable Diffusion과 동일한 텍스트 CLIP을 사용한다. 텍스트 CLIP은 77개의 벡터를 출력하고 각각은 768차원이다. 학습을 용이하게 하기 위해 linear layer를 추가하여 각 벡터의 차원을 64로 줄여 $y_0$를 임베딩하는 최종 텍스트를 얻는다. GPT-2를 기반으로 텍스트 디코더 \(\mathcal{D}^\textrm{text}\)를 구성한다. 특히 GPT-2는 $y_0$을 접두사 임베딩으로 사용하고 텍스트를 autoregressive하게 재구성한다. CLIP의 파라미터를 고정한 후 linear layer를 학습하고 GPT-2를 fine-tuning하여 입력 텍스트를 재구성한다.

Remark

저자들은 이미지와 텍스트의 latent 임베딩이 이미 유사하고 합리적인 수치 범위를 가지고 있음을 관찰하였다. 구체적으로, $[-2, 2]$의 범위 내에 집중되어 있으며 비슷한 평균과 분산 값으로 대략적인 정규 분포를 나타낸다. 결과적으로 추가 정규화를 적용하지 않았다. 더 많은 modality의 경우 latent space에 정규화가 있는 인코더를 통해 이를 연속적인 latent feature로 유사하게 변환할 수 있다. 이렇게 하면 정규화 후 모든 modality가 유사한 범위를 쉽게 가질 수 있다. 게다가 고품질 인코더와 디코더를 얻는 것은 비교적 간단하며 적은 양의 데이터로도 달성할 수 있다. 예를 들어, 이미지 인코더와 디코더의 데이터셋 크기는 UniDiffuser의 1% 미만이다. 따라서 실제로 필요한 경우 적절한 비용으로 각 modality에 대한 고품질 인코더와 디코더를 효율적으로 학습시킬 수 있다.

2. Transformer as Joint Noise Prediction Network

임베딩에서 공동 noise 예측 네트워크를 학습시킨다. 다양한 modality의 입력을 처리하기 위해 UniDiffuser에서 transformer 기반 backbone을 사용하는 것은 자연스럽다. 특히 조건부 diffusion model을 위해 최근에 제안된 transformer인 U-ViT를 채택한다. 원래 U-ViT는 데이터, 조건, timestep을 포함한 모든 입력을 토큰으로 처리하고 얕은 레이어와 깊은 레이어 사이에 긴 skip connection을 사용하는 것이 특징이다.

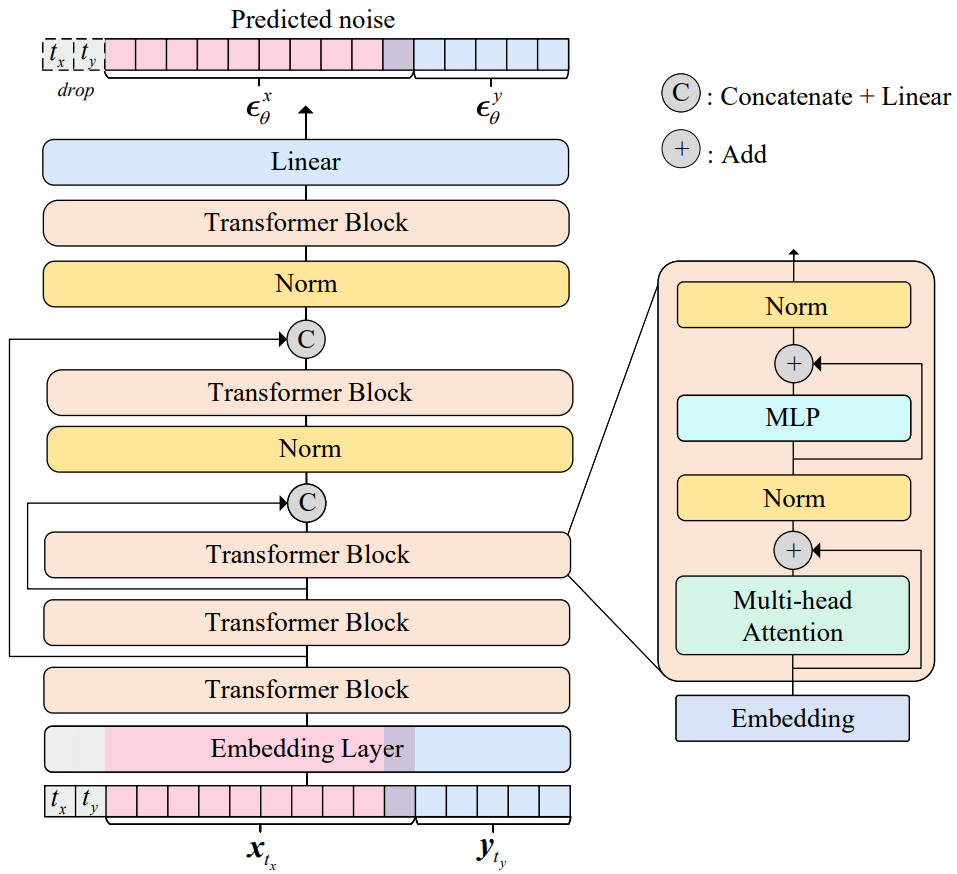
UniDiffuser에서는 두 가지 데이터 modality와 해당 timestep을 토큰으로 처리하여 U-ViT를 약간 수정한다. 또한 저자들은 원래 U-ViT의 pre-layer normalization가 mixed precision로 학습될 때 쉽게 overflow를 유발한다는 것을 경험적으로 발견했다. 간단한 해결책은 post-layer normalization을 사용하고 긴 skip connection을 연결한 후 레이어 정규화를 추가하여 UniDiffuser의 학습을 안정화하는 것이다. 아래 그림은 backbone을 설명한다.

Experiments

• 데이터셋: LAION-5B

다음은 UniDiffuser와 Versatile Diffusion (VD)을 text-to-image 생성에 대하여 비교한 그래프이다.

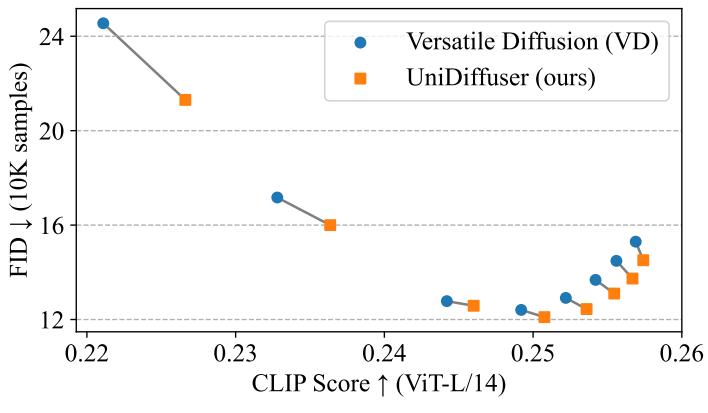
다음은 UniDiffuser와 VD를 image-to-text 생성에 대하여 비교한 그래프이다.

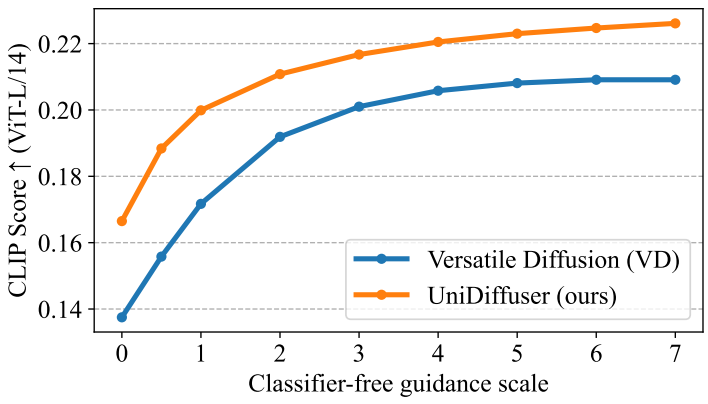
다음은 text-to-image 생성에 대한 UniDiffuser와 VD의 랜덤 샘플들이다.

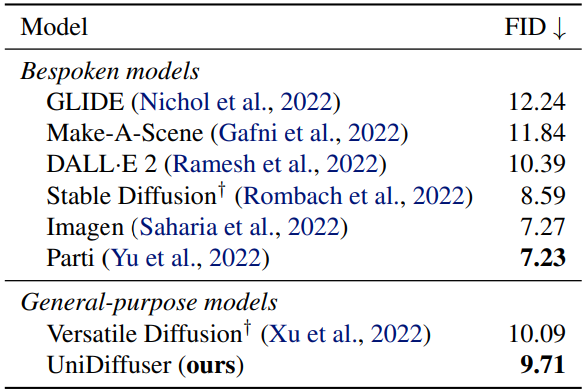
다음은 MS-COCO validation set에서의 zero-shot FID를 비교한 표이다.