[논문리뷰] UDPM: Upsampling Diffusion Probabilistic Models
arXiv 2023. [Paper] [Github]
Shady Abu-Hussein, Raja Giryes
Tel Aviv University
25 May 2023
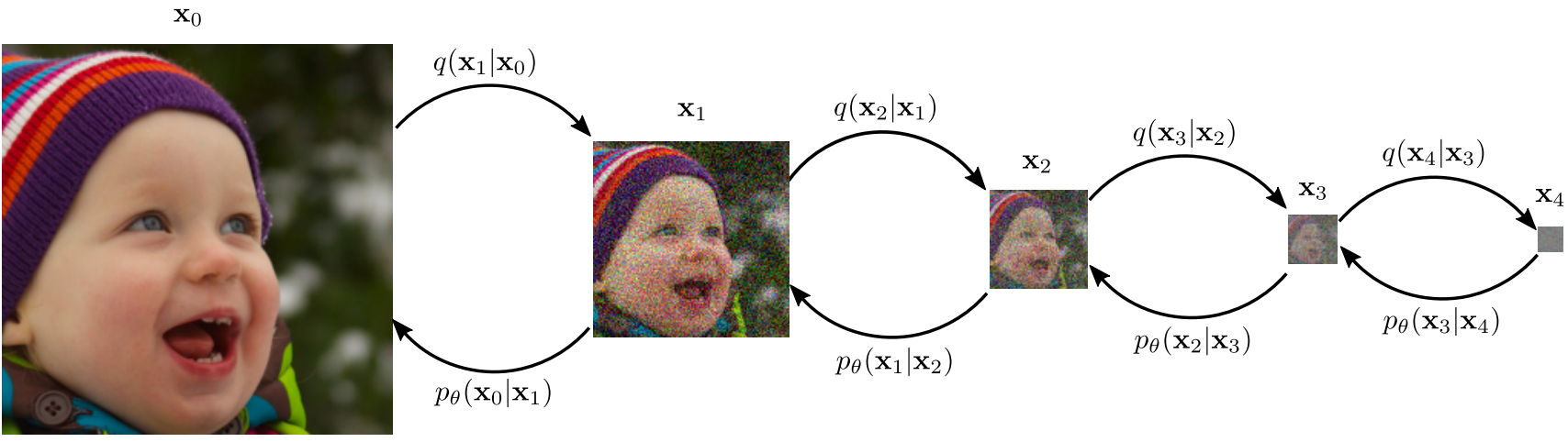
Introduction
최근 몇 년 동안 DDPM은 복잡한 데이터 분포를 학습하고 고품질 이미지를 생성하는 능력으로 인해 이미지 생성에 널리 사용되는 방법이 되었다. DDPM의 기본 원리는 데이터 샘플로 시작하여 순수한 white noise에 도달할 때까지 Markovian process를 통해 점진적으로 noise를 추가하는 것이다. 이 프로세스는 forward process로 알려져 있으며 $q(x_{0:L})$로 정의된다. 새로운 샘플을 생성하기 위해 사용되는 reverse process는 심층 신경망을 사용하여 학습된 $p_\theta (x_{0:L})$로 정의된다. 이 프로세스를 통해 학습 데이터 분포에서 인상적인 성능을 얻을 수 있다.
DDPM은 이미지 생성에서 인상적인 결과를 보여주었지만 몇 가지 제한 사항이 있다. 한 가지 주요 제한 사항은 만족스러운 샘플을 생성하기 위해 많은 수의 diffusion step이 필요하다는 것이다. 이는 상당히 계산 집약적일 수 있으므로 학습 프로세스가 느리고 자원 집약적이다. 현재의 SOTA 방법은 샘플링 step 수를 크게 줄이지만 10 step 미만으로 낮추면 성능에 큰 영향을 미친다.
또한 diffusion model의 latent space는 보간(interpolation)이 불가능하므로 특히 unconditional 세팅에서 사용될 때 동영상 생성 또는 애니메이션과 같은 특정 유형의 이미지 생성 task에 대한 유용성이 제한된다. Diffusion model을 사용하여 편집하는 데 사용되는 대부분의 편집 task는 latent space 자체가 아니라 함께 사용되는 CLIP 임베딩 조작에 의존한다.
따라서 본 연구에서는 Upsampling Diffusion Probabilistic Model (UDPM)이라는 DDPM에 대한 일반화 방식을 제안한다. Forward diffusion model을 noise 증가로 제한하는 대신 noise 레벨을 높이는 것 외에도 서브샘플링으로 일반화한다. 전반적으로 UDPM은 고품질 이미지를 생성하는 데 필요한 diffusion step의 수를 줄이면서 latent space의 보간 가능성을 증가시킴으로써 현재의 SOTA 방법에 비해 상당한 개선을 제공한다.
Method
전통적인 DDPM은 확률적 Markov process가 다음과 같이 정의된다고 가정한다.
\[\begin{equation} q (x_l \vert x_{l-1}) := \mathcal{N} (\sqrt{1 - \beta_l} (x_{l-1}), \beta_l I) \\ p_\theta (x_{l-1} \vert x_l) := \mathcal{N} (\mu_\theta^{(l)} (x_l), \Sigma_\theta^{(l)} (x_l)) \end{equation}\]이 방정식은 각각 noise를 추가하고 제거하여 진행되는 forward process와 reverse process를 구성한다. 본 논문에서는 forward process에서 degradation(열화) 요소를 추가하여 이 방식을 일반화하는데, 여기서 forward process에서 가변 공간 차원을 서브샘플링하고 reverse process에서 업샘플링한다.
1. Upsampling Diffusion Probabilistic Model
Forward process와 reverse process의 주변 분포를 다음과 같이 재정의한다.
\[\begin{equation} q (x_l \vert x_{l-1}) := \mathcal{N} (\sqrt{1 - \beta_l} \mathcal{H} (x_{l-1}), \beta_l I) \\ p_\theta (x_{l-1} \vert x_l) := \mathcal{N} (\mu_\theta (x_l, l), \Sigma_l) \end{equation}\]여기서 $\mathcal{H} = I$를 사용한 이전 diffusion model들과 달리, 본 논문에서는 연산자 $\mathcal{H}$를 다운샘플링 연산자로 정의하고, blur 필터 $\mathcal{W}$를 적용한 다음 stride $\gamma$로 서브샘플링을 적용하여 정의한다. 결과적으로 forward process는 증가된 noise 레벨 외에도 변수의 차원을 줄인다.
Diffusion model은 $p_\theta (x_0)$의 기댓값을 최대화하는 것이 목표이며, 이는 ELBO를 통해 가능하다.
\[\begin{aligned} \mathbb{E} [-\log p_\theta (x_0)] &\le \mathbb{E}_q \bigg[ -\log \frac{p_\theta (x_{0:L})}{q(x_{1:L})} \bigg] \\ &= \mathbb{E}_q [D_\textrm{KL} (p(x_L) \;\|\; q(x_L \vert x_0)) \\ &+ \sum_{l=2}^L D_\textrm{KL} (p_\theta (x_{l-1} \vert x_l) \;|\; q(x_{l-1} \vert x_l, x_0)) \\ &- \log p_\theta (x_1 \vert x_0)] \end{aligned}\]위 식의 우변은 기울기 하강법을 사용하여 $\theta$에 대해 확률적으로 최소화할 수 있으며, 여기서 각 step에서 임의의 $t$가 선택되므로 단일 항이 최적화된다.
$p_\theta (\cdot)$의 학습에 위 식을 사용할 수 있으려면 명시적으로 $q(x_{l−1} \vert x_l, x_0)$를 찾아야 하며, 먼저 $q(x_l \vert x_0)$을 얻은 다음 베이즈 정리를 사용하여 $q(x_{l−1} \vert x_l, x_0)$를 유도할 수 있다. 이를 위해 저자들은 다음 Lemma 1을 제안하였다.
Lemma 1. \(e \overset{iid}{\sim}$ \mathcal{N} (0,I) \in \mathbb{R}^N\)이고 \(\mathcal{H} = \mathcal{S}_\gamma \mathcal{W}\)라고 하자. 여기서 \(\mathcal{S}_\gamma\)는 stride가 $\gamma$인 서브샘플링 연산자이고 $\mathcal{W}$는 blur kernel $w$를 사용하는 blur 연산자이다. 그러면, 만일 $w$의 지원이 최대 $\gamma$이면 \(\mathcal{H} e \overset{iid}{\sim} \mathcal{N}(0, \|w\|_2^2 I)\)이다.
Lemma 1을 만족하고, $|w|_2^2 = 1$이라고 가정하면 다음 결과를 얻을 수 있다.
\[\begin{equation} q(x_l \vert x_0) = \mathcal{N} (\sqrt{\vphantom{1} \bar{\alpha}_l} \mathcal{H}^l x_0, (1 - \bar{\alpha}_l) I) \\ \textrm{where} \quad \alpha_l = 1 - \beta_l, \quad \bar{\alpha}_l = \prod_{k=0}^l \alpha_k \end{equation}\]위 식을 사용하면 $x_0$에 단순히 $\mathcal{H}$를 $l$번 적용하고 기존의 DDPM의 noising 방식을 사용하여 $x_l$을 얻을 수 있다.
$q(x_l \vert x_0)$이 주어지면, 베이즈 정리와 Markov chain 속성을 사용하여 $q(x_{l-1} \vert x_l, x_0)$를 구할 수 있다.
\[\begin{aligned} q(x_{l-1} \vert x_l, x_0) &= \frac{q(x_l \vert x_{l-1}, x_0) q(x_{l-1}, x_0)}{q(x_l, x_0)} \\ &= \frac{q(x_l \vert x_{l-1}, x_0) q(x_{l-1} \vert x_0) q(x_0)}{q(x_l \vert x_0) q(x_0)} \\ &= \frac{q(x_l \vert x_{l-1}, x_0) q(x_{l-1} \vert x_0)}{q(x_l \vert x_0)} \\ &= \frac{q(x_l \vert x_{l-1}) q(x_{l-1} \vert x_0)}{q(x_l \vert x_0)} \end{aligned}\]위 식을 이용하면 다음을 얻을 수 있다.
\[\begin{equation} q(x_{l-1} \vert x_l, x_0) = \mathcal{N} (\mu (x_l, x_0, l), \Sigma_l) \\ \Sigma_l = \bigg( \frac{\alpha_l}{\beta_l} \mathcal{H}^\top \mathcal{H} + \frac{1}{1 - \bar{\alpha}_{l-1}} I \bigg)^{-1} \\ \mu (x_l, x_0, l) = \Sigma_l \bigg( \frac{\sqrt{\alpha_l}}{\beta_l} \mathcal{H}^\top x_l + \frac{\sqrt{\vphantom{1} \bar{\alpha}_{l-1}}}{1-\bar{\alpha}_{l-1}} \mathcal{H}^{l-1} x_0 \bigg) \end{equation}\]$\Sigma_l$은 다루기 어려워 보이지만, 실제로 이산 푸리에 변환과 poly-phase filtering 항등식을 사용하여 쉽게 구현할 수 있다. 여기서 $\mathcal{H}^\top \mathcal{H}$는 $w$와 $w$의 뒤집힌 버전 사이의 convolution과 동일하며, stride $\gamma$의 서브샘플링이 이어진다.
Posterior $q(x_{l−1} \vert x_l, x_0)$는 파라미터 $(\mu(x_l, x_0, l), \Sigma_l)$과 함께 정규 분포이다. 따라서 $p_\theta (\cdot)$도 파라미터 $(\mu_\theta, \Sigma_l)$로 이루어진 정규 분포라고 가정한다. 여기서 $\mu_\theta$는 학습된 파라미터 $\theta$를 갖는 신경망에 의해 parameterize된다.
정규 분포의 경우 ELBO의 단일 항은 아래와 동등하다.
\[\begin{aligned} \ell^{(l)} &= D_\textrm{KL} (p_\theta (x_{l-1} \vert x_l) \;\|\; q(x_{l-1} \vert x_l, x_0)) \\ &= C_l + \frac{1}{2} (\mu_\theta - \mu_l)^\top \Sigma_l^{-1} (\mu_\theta - \mu_l) \end{aligned}\]여기서 $C_l$은 $\theta$에 의존하지 않는 상수이다.
저자들은 $\mu$를 예측하기 위해 $p_\theta$를 학습시키면 결과가 더 나빠지는 것을 실험으로 확인하였다. 따라서 $\mu(x_l, x_0, l)$의 두 번째 항, 즉 $\mathcal{H}^{l-1} x_0$를 $x_l$에서 예측하도록 네트워크를 학습시킨다. 그 결과, $\ell^{(l)}$을 최소화하는 것은 다음 항을 최소화하는 것으로 단순화될 수 있다.
\[\begin{equation} \tilde{\ell}_\textrm{simple}^{(l)} = (f_\theta (x_l) - \mathcal{H}^{l-1} x_0)^\top \Sigma_l (f_\theta (x_l) - \mathcal{H}^{l-1} x_0) \end{equation}\]여기서 $f_\theta (\cdot)$은 신경망이다. $\Sigma_l$의 정의에 의해 $\Sigma_l$이 양의 대각행렬임을 알 수 있으며, 따라서 $\Sigma_l$을 위 식에서 지울 수 있다. 또한, 다운샘플링된 버전 $\mathcal{H}^{l-1} x_0$ 대신 $x_0$를 예측하는 것이 더 낫다고 한다. 결과적으로 목적 함수를 다음과 같이 단순화할 수 있다.
\[\begin{equation} \ell_\textrm{simple}^{(l)} = \|f_\theta (x_l) - x_0 \|_2^2 \end{equation}\]학습 절차는 Algorithm 1에 요약되어 있다.

2. Image Generation using UDPM
$x_l$에서 $x_0$을 예측하도록 학습된 신경망 $f_\theta$가 주어지면 순수한 일반 noise 샘플 $x_L \sim \mathcal{N}(0, I)$으로 시작한다. 그 후 \(\hat{x}_0 := f_\theta (x_l)\)을 $\mu(x_l, x_0, l)$ 식에 대입하면 $\mu_L$을 추정할 수 있다. 그런 다음 $\mathcal{N}(\mu_L, \Sigma_L)$에서 샘플링하여 다음 reverse diffusion step $x_{L-1}$을 얻을 수 있다. 이러한 step을 $L$번 반복하면 샘플 $x_0 \sim p_\theta (x_0)$를 얻을 수 있다.
Posterior를 샘플링하려면 다음과 같은 형식으로 $\mathcal{N} (\mu_l, \Sigma_l)$을 parameterize해야 한다.
\[\begin{equation} x_{l-1} + \mu_l + \Sigma_l^{\frac{1}{2}} e, \quad e \sim \mathcal{N}(0, I) \end{equation}\]이를 위해서는 $\Sigma_l^{\frac{1}{2}}$을 엑세스힐 수 있어야 하며 $\Sigma_l$의 구조로 인해 $e$에 효율적으로 적용할 수 있다. 샘플링 절차는 Algorithm 2에 요약되어 있다.

학습과 샘플링 절차에 대한 개요는 아래 그림에 나와 있다.

Experiments
- 데이터셋: FFHQ, AFHQv2, LSUN horses, ImageNet
- Hyperparameter
- $\gamma = 2$
- $x_L$이 2$\times$2가 되도록 $L = \log_2 (\min (H, W)) - 1$로 설정. ($H$, $W$는 데이터셋 이미지의 높이와 너비)
- $w$: 크기가 2$\times$2인 uniform box filter
- $\mathcal{H}$의 downsampling factor: $s(l) = \gamma^{\lceil L \times l \rceil}$
- noise schedule:
1. Unconditional Generation
다음은 AFHQ 256$\times$256와 FFHQ 128$\times$128에 대하여 UDPM으로 생성된 이미지들이다. 각각 7개와 6개의 diffusion step만을 사용하였다.

다음은 latent space에서 보간한 예시이다.

다음은 latent space perturbation에 대한 결과이다. 가장 왼쪽의 이미지가 원본 이미지이고, 나머지는 diffusion step $l$에서 latent noise에 작은 noise를 추가하여 생성된 것이다. 두번째 열의 이미지가 $l = L$에 해당하고 마지막 열의 이미지가 $l = 1$에 해당한다.

2. Classes conditional generation
다음은 ImageNet 64$\times$64애 대하여 UDPM으로 생성된 이미지이다. $L = 5$이고 classifier-free guidance scale은 위는 1.5, 아래는 3.0이다.


3. Limitation
UDPM으로 얻은 결과는 다른 diffusion model보다 부드럽다. 그러나 저자들은 이것이 계산상의 제약 때문이라고 생각한다. 학습 중에 batch 크기와 iteration 횟수를 늘리면 모델이 계속 개선되고 더 선명한 결과를 얻는 것을 볼 수 있다. 그러나 리소스 부족으로 인해 학습 iteration 횟수와 사용할 수 있는 데이터 크기가 제한되어 있다. 그럼에도 불구하고 UDPM은 훨씬 적은 iteration을 사용하고 다른 diffusion model에는 없는 보간 가능한 latent space가 있다.