[논문리뷰] U-DiT TTS: U-Diffusion Vision Transformer for Text-to-Speech
INTERSPEECH 2023. [Paper] [Page]
Xin Jing, Yi Chang, Zijiang Yang, Jiangjian Xie, Andreas Triantafyllopoulos, Bjoern W. Schuller
University of Augsburg | Beijing Forestry University | GLAM
22 May 2023
Introduction
TTS는 텍스트를 음성 언어로 변환하도록 설계된 컴퓨터 기반 시스템으로, 인간-컴퓨터 상호 작용(HCI)에서 널리 사용되어 왔다. 최근 몇 년 동안 딥러닝 기술의 극적인 발전으로 인해 보다 자연스럽게 들리는 음성이 합성되었다.
최신 DNN(심층 신경망) 기반 TTS 시스템은 일반적으로 acoustic model (음향 모델)과 vocoder의 두 가지 주요 구성 요소로 구성되므로 표준 파이프라인의 두 초기 단계를 하나의 모델에 통합한다. Acoustic model은 입력 텍스트를 시간-주파수 도메인 acoustic feature로 변환한 다음 vocoder가 이러한 acoustic feature로 컨디셔닝된 파형을 합성한다. Tacotron 2가 도입된 이후로 mel-spectrogram은 대부분의 최신 TTS 시스템에서 지배적인 acoustic feature가 되었다.
Sequence-to-sequence (seq2seq) 아키텍처에서 프레임별로 mel-spectrogram을 직접 생성하는 대신 생성 모델은 음성 신호의 latent 분포를 학습하고 여기에서 샘플링하여 새로운 신호를 합성하는 것을 목표로 한다. VAE, GAN, flow 기반 생성 모델은 입력 텍스트와 음성 간의 기본 관계를 캡처하는 능력을 활용하여 보다 자연스럽고 일관되며 빠른 음성 합성을 생성했다.
최근 diffusion model이라고도 하는 score 기반 생성 모델 (SGM)은 많은 연구 분야에서 SOTA 성능을 달성했다. SGM은 계획된 noise를 반복적으로 추가하여 복잡한 데이터 분포를 점차 단순한 분포 (일반적으로 정규 분포)로 바꿀 수 있다는 단순하지만 효과적인 아이디어를 기반으로 한다. 한편, 역시간 forward process의 궤적을 따라 이 절차를 반전하도록 신경망을 학습할 수 있다. 이러한 SGM에서 수정된 U-Net 아키텍처는 이 diffusion model로 적합하다는 것이 입증되었다. 추가적인 공간적 self-attention 블록으로 로컬 및 글로벌 feature를 모두 캡처하는 기능은 연구 분야에서 널리 채택되었다. U-Net 아키텍처의 추가 개선으로 Diffusion Visual Transformer (DiT)는 ViT를 diffusion model의 backbone으로 도입했으며 클래스 조건부 ImageNet 벤치마크에서 SOTA 이미지 생성 성능을 달성했다.
본 논문에서는 U-DiT 아키텍처를 제안하여 diffusion 기반 TTS 시스템의 백본에서 핵심 구성 요소로 ViT 변환의 가능성을 탐색한다. U-Net과 ViT의 속성을 결합함으로써 객관적인 결과와 MOS 결과 모두 U-DiT TTS가 최신 diffusion 기반 TTS 시스템에 비해 더 높은 품질의 음성과 더 자연스러운 운율을 생성한다는 것을 보여준다.
Score-based Generative Models
Score 기반 생성 모델 (SGM)은 확률적 미분 방정식 (SDE) 공식을 채택하는 통합 프레임워크이다. SGM은 다수의 noisy한 데이터 분포에서 log 확률 밀도 함수 (score function)의 기울기를 학습한 다음 Langevin 역학이라는 반복 절차로 샘플을 생성할 수 있는 생성적 diffusion model 클래스이다. Langevin 역학은 확률 분포에서 샘플을 생성하는 Markov Chain Monte Carlo (MCMC) 알고리즘이다.
1. SGMs with stochastic differential equations
한정된 수의 noise 분포 대신 SGM은 diffusion process에 따라 시간이 지남에 따라 진화하는 분포의 연속체로 학습 데이터를 교란시키고 forward process \(\{x_t\}_t\)는 Ito SDE로 설명할 수 있다.
\[\begin{equation} dx_t = f(x_t, t)dt + g(t)dw \end{equation}\]여기서 $f$와 $g$는 각각 $x(t)$의 drift coefficient와 diffusion coefficient이며, $w$는 표준 Wiener process (브라운 운동)이다. $t$는 process step을 나타내며 오디오 또는 오디오의 변환된 버전의 시간 축과 무관하다.
위 식의 모든 SDE에는 대응하는 reverse SDE가 있으며, 이는 diffusion process이기도 하다.
\[\begin{equation} dx_t = [f (x_t, t) - g (t)^2 \nabla_{x_t} \log p_t (x_t)] dt + g(t) d \bar{w} \end{equation}\]여기서 $dt$는 음의 극소 timestep이며 $\bar{w}$는 $t$가 $T$에서 0으로 가는 표준 Wiener process이다. $\nabla_{x_t} \log p_t (x_t)$는 prior 분포 $p(x)$의 score function이며 학습된 score 기반 모델 $s_\theta$에 의해 근사된다.
\[\begin{equation} s_\theta (x_t, t) \approx \nabla_{x_t} \log p_t (x_t) \end{equation}\]2. Diffusion Process in TTS systems
Forward Process: 위에서 언급한 바와 같이, 입력 데이터를 prior 분포로 손상시키기 위해 forward SDE diffusion process를 먼저 정의해야 한다. 본 논문에서는 forward SDE가 다음과 같이 정의되는 Grad-TTS의 forward diffusion process를 따른다.
\[\begin{equation} dX_t = \frac{1}{2} \Lambda^{-1} (\mu - X_t) \beta_t dt + \sqrt{\beta_t} dW_t, \quad t \in [0, T] \end{equation}\]여기서 $\beta_t$는 noise schedule function이며, $\mu$는 벡터, $\Lambda$는 양의 원소를 가지는 대각 행렬이다.
$I$를 항등 행렬이라고 하면 prior 분포는 다음과 같이 정의할 수 있다.
\[\begin{equation} p_{0t} \{X_t \vert X_0, \mu\} = \mathcal{N} (X_t; \rho (X_0, \Lambda, \mu, t), \delta (\Lambda, t)^2 I) \end{equation}\]이는 Ornstein-Uhlenbeck SDE이며, SDE의 평균 $\rho (\cdot)$와 분산 $\delta (\cdot)^2$는 다음과 같이 closed form으로 얻을 수 있다.
\[\begin{aligned} \rho (X_0, \Lambda, \mu, t) =\;& \bigg( I - \exp \bigg( - \frac{1}{2} \Lambda^{-1} \int_0^t \beta_s ds \bigg) \bigg) \mu \\ &+ \exp \bigg( - \frac{1}{2} \Lambda^{-1} \int_0^t \beta_s ds \bigg) X_0 \\ \delta (\Lambda, t) I =\;& \Lambda \bigg( I - \exp \bigg( \Lambda^{-1} \int_0^t \beta_s ds \bigg) \bigg) \end{aligned}\]Reverse Process: Diffusion process 식에서 reverse process에 대한 reverse SDE를 얻을 수 있다. 그러나 reverse process를 단순화하고 속도를 높이기 위해 probability flow ordinary differential equation (ODE)를 사용하며, 이는 다음과 같은 역 방정식으로 이어진다.
\[\begin{equation} dX_t = \bigg( \frac{1}{2} \Lambda^{-1} (\mu - X_t) - \nabla \log p_t (X_t) \bigg) \beta_t dt \end{equation}\]System Overview
본 논문에서는 diffusion process를 위해 설계된 ViT 변형 중 하나인 U-DiT 아키텍처를 제안한다. 이 새로운 아키텍처는 높은 수준의 semantic feature와 mel-spectrogram의 세분화된 디테일을 모두 효과적으로 캡처하도록 설계되어 음성 합성 task의 성능을 향상시킨다.
1. DiT blocks
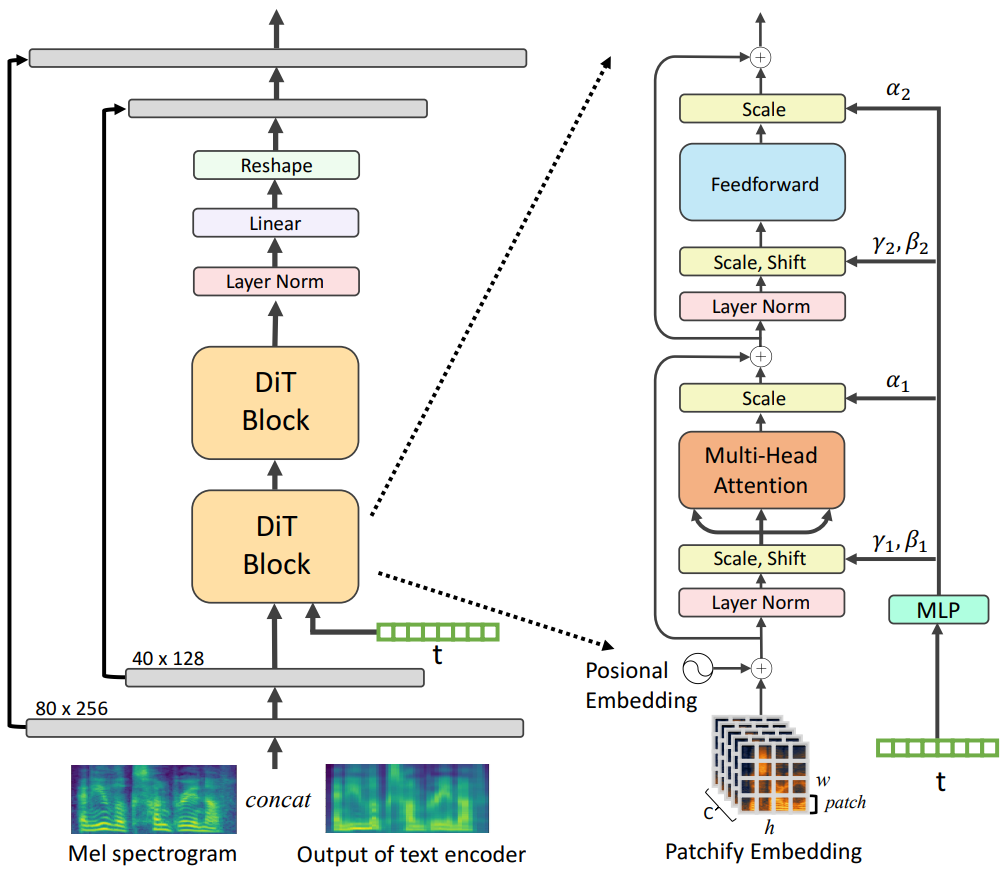
위 그림은 제안된 DiT 블록의 세부 디자인을 보여준다. DiT 블록은 ViT 블록 설계의 모범 사례를 유지하면서 표준 ViT 블록에 약간의 사소하지만 중요한 수정이 이루어졌다.
Patchify: DiT는 입력을 ViT와 같은 일련의 토큰으로 변환한다. 그런 다음 frequency 기반 위치 임베딩이 모든 토큰에 적용된다. 모델에서 패치 크기를 $[20, 64]$로 설정했다.
Layer Normalization: 데이터 포인트의 집합을 정규화하면 일반화를 개선할 수 있는 비슷한 스케일로 변환된다. 특히 Adaptive Layer Normalization (adaLN)은 중간 레이어의 분포를 정규화하여 더 부드러운 기울기와 더 나은 일반화 정확도를 가능하게 한다. GAN 아키텍처와 표준 diffusion U-Net backbone에서 널리 활용되었다. 또한 diffusion U-Net 백본은 residual connection 전에 최종 convolution layer에 대해 zero-initialization 전략을 사용하며, 이는 다른 task들에 대한 대규모 학습을 가속화하는 것으로 밝혀졌다. adaLN-Zero라는 두 기술의 조합은 DiT 성능을 더욱 향상시키고 이미지 합성에 대한 일반화를 위한 강력한 설계임이 입증되었다.
Embedding MLP: Diffusion process는 매우 강력하게 시간과 레이블에 의존적이기 때문에 (라벨이 존재하는 경우), 시간 임베딩 벡터 $t_e$와 레이블 임베딩 $l_e$ 벡터의 합에서 shift 파라미터 $\gamma$와 $\beta$를 회귀하기 위해 4-layer MLP가 적용되었다. 또한, DiT 블록 내의 residual connection 이전에 적용되는 차원별 스케일링 파라미터 $\alpha$도 동일한 MLP 블록에 의해 회귀된다.
2. Latent space for U-DiT
저자들은 처음에 고해상도 픽셀 space에서 diffusion model의 backbone으로 DiT 아키텍처를 적용하였다. 그러나 이로 인해 잡음이 많고 일관성이 결여된 음성이 생성되었다. 이 문제를 해결하기 위해 먼저 DDPM에서 U-Net 아키텍처의 다운샘플링 및 업샘플링 구성 요소를 활용하여 입력 spectrogram을 latent space 표현으로 변환한 다음 DiT 블록의 입력으로 사용한다. 다운샘플링 부분의 각 레이어는 입력에서 낮은 레벨의 feature를 추출하기 위해 group normalization를 사용하는 여러 residual block으로 구성되며, 다음 self-attention 레이어에서 처리된다. 그 후, latent space feature는 작은 패치로 분할되고 이러한 패치의 공간 정보는 sinusoidal position embedding으로 인코딩된다. 마지막으로 다운샘플링 부분과 대칭 구조를 갖는 업샘플링 부분은 latent space feature를 원래 크기로 복원한다.
3. Model Architechure
저자들은 GlowTTS와 Grad-TTS의 구조를 기반으로 TTS 시스템을 구축한다. 따라서 U-DiT TTS 시스템은 텍스트 인코더, duration predictor, 디코더의 세 가지 상호 관련된 구성 요소로 구성된다.
Text Encoder: 텍스트 인코더는 pre-net, multi-head self-attention이 있는 6개의 transformer 블록, linear projection layer로 구성된다. Pre-net은 convolution layer 3개와 fully-connected layer로 구성된다. 이 아키텍처는 나머지 TTS 시스템에서 사용할 수 있는 입력 텍스트의 의미 있는 feature를 효과적으로 캡처하도록 설계되었다.
Duration predictor: 본 논문에서는 GlowTTS를 따라 텍스트와 해당 음성 간의 최적의 단조로운 전사 정렬을 찾기 위해 Monotonic Alignment Search (MAS) 함수라는 반복적 접근 방식을 적용한다. 또한 입력 텍스트의 각 요소의 duration을 예측하는 Fastspeech 2의 duration predictor 네트워크를 적용한다.
Decoder: 디코더에서는 2-layer UNet 다운샘플링 및 업샘플링 구성 요소를 사용한다. 또한 저자들은 2, 4 및 8을 포함하여 다양한 수의 DiT 블록으로 테스트했으며, 모델 크기가 클수록 사용 가능한 데이터 양이 제한되어 성능이 저하될 수 있음을 발견했다. 따라서 저자들은 2개의 DiT 블록을 사용하기로 결정했다. Vocoder의 경우 HiFi-GAN을 사용하여 재구성된 mel-spectrogram에서 최종 음성을 생성한다.
Training Objectives
목적 함수는 주어진 입력에 대해 원하는 결과를 향해 모델의 학습을 안내하는 데 중요하다. 모델 아키텍처를 따라 TTS 시스템 성능을 공동으로 최적화하기 위한 3가지 loss function이 있다.
Encoder loss: 본 논문에서는 noise가 대각 공분산을 갖는 가우시안 분포에서 생성된다고 가정한다. 이는 여러 수학적 유도를 단순화하여 여러 TTS 시스템에서 효과적인 것으로 입증되었다. 따라서 텍스트 인코더 출력을 독립적인 정규 분포
\[\begin{equation} \tilde{\mu}_{A_{(i)}} \sim \mathcal{N} (\tilde{\mu}_{A_{(i)}}, I) \end{equation}\]로 설정할 수 있으며 이는 다음과 같은 negative log-likelihood encoder loss로 이어진다.
\[\begin{equation} \mathcal{L}_\textrm{enc} = - \sum_i^N \log \phi (y_i; \tilde{\mu}_{A_{(i)}}, I) \end{equation}\]여기서 $\tilde{\mu}$는 텍스트 인코더 출력이고 $\phi (\cdot, \mu, I)$는 정규 분포 $\mathcal{N} (\mu, I)$의 확률 밀도 함수이다. 효율성을 더욱 향상시키기 위해 \(\mathcal{L}_\textrm{enc}\)를 로그 도메인에 설정하여 \(\mathcal{L}_\textrm{enc}\)를 평균 제곱 오차(MSE) loss로 만든다.
Duration loss: 또한 로그 도메인에서 MSE loss를 사용하여 Duration Predictor loss $\textrm{DP}$를 학습한다.
\[\begin{equation} d_i = \log \sum_{j=1}^{N_\textrm{freq}} 1_{A^\ast (j) = i}, \quad i = 1, \cdots, N_\textrm{freq} \\ \mathcal{L}_\textrm{DP} = \textrm{MSE} (\textrm{DP} (\textrm{sg} [\tilde{\mu}], d)) \end{equation}\]여기서 $\textrm{sg}[\cdot]$는 텍스트 인코더 매개변수에 영향을 미치는 \(\mathcal{L}_\textrm{DP}\)를 방지하는 데 사용되는 stop-gradient 연산자이다. Stop-gradient 연산을 사용하면 duration predictor가 있는 텍스트 인코더가 디코더 없이 독립적으로 학습될 수 있는 것으로 보인다. 그러나 이는 정렬 실패와 함께 비효율적인 학습 프로세스로 이어질 뿐이다.
Diffusion loss: Score model $s_\theta (x_t, t)$를 학습하여 noisy한 데이터 $X_t$의 로그 밀도 기울기를 추정하는 것이 목표이다.
\[\begin{equation} \mathcal{L}_t (X_0) = \mathbb{E}_{\epsilon_t} [\| s_\theta (X_t, t) + \lambda (\Lambda, t)^{-1} \epsilon_t \|_2^2] \end{equation}\]여기서 $X_0$는 시간 $t \in [0, T]$의 학습 데이터에서 샘플링된 타겟 spectrogram이며 균일 분포 $\xi_t \sim \mathcal{N} (0, I)$에서 샘플링되고 $X_t$는 다음에서 샘플링할 수 있다.
\[\begin{equation} X_t = \rho (X_0, I, \mu, t) + \sqrt{\lambda_t} \xi_t \end{equation}\]이미 $\Lambda = I$로 설정하여 noise 분포를 단순화했다. Noise 분포의 공분산 행렬은 항등 행렬 $I$에 스칼라
\[\begin{equation} \lambda_t = 1 - \exp \bigg(\int_0^t \beta_s ds \bigg) \end{equation}\]를 곱한 것이다. 마지막으로 diffusion loss function은 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{diff} \mathbb{E}_{X_0, t} \bigg[ \lambda_t \mathbb{E}_t \bigg[ \bigg\| s_\theta (X_t, \mu, t) + \frac{\xi_t}{\sqrt{\lambda_t}} \bigg\| \bigg] \bigg] \end{equation}\]Experiments
- 데이터셋: LJSpeech 데이터셋
- 실험 세팅
- 오디오 feature 생성: 80 차원 mel-spectrogram (1024 window length, 256 hop length)
- 입력 텍스트는 CMU 발음 사전에 의해 음소로 변환됨
- noise schedule: Grad TTS와 동일하게 $\beta_t = 0.05 + (20 - 0.05) t$, $t \in [0, 1]$
- 학습
- optimizer: Adam
- learning rate: $10^{-4}$
- batch size: 32
- gradient clipping을 적용해 기울기 폭발 방지
- Inference
- Transformer 아키텍처의 입력 크기 제한을 해결하기 위해 입력 텍스트를 분할
- 총 음소 수가 22와 25 사이에 있을 때 텍스트 인코더의 출력 길이가 256보다 약간 작기 때문에 텍스트 음소 분할 길이를 이 범위로 조정
- $\mathcal{N} (\mu, I)$에서 $x_T$를 샘플링하는 대신 hyperparameter $\tau$를 적용하고 $\mathcal{N} (\mu, I/\tau)$에서 샘플링
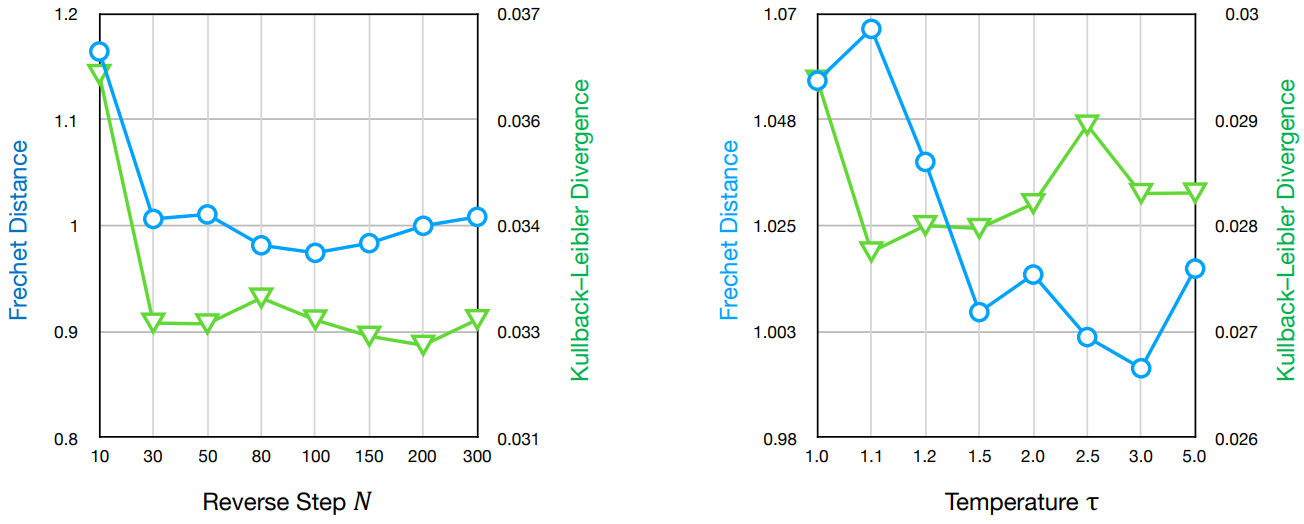
- reverse step = 80, temperature $\tau = 1.5$
1. Results
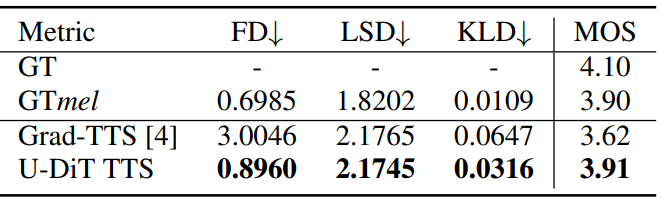
다음은 LJSpeech test set에서 성능을 비교한 표이다.
2. Ablation study
다음은 reverse step $N$과 temperature $\tau$에 따른 성능을 비교한 그래프이다.