[논문리뷰] TTT3R: 3D Reconstruction as Test-Time Training

arXiv 2025. [Paper] [Page] [Github]
Xingyu Chen, Yue Chen, Yuliang Xiu, Andreas Geiger, Anpei Chen
Westlake University | University of Tübingen, Tübingen AI Center
30 Sep 2025

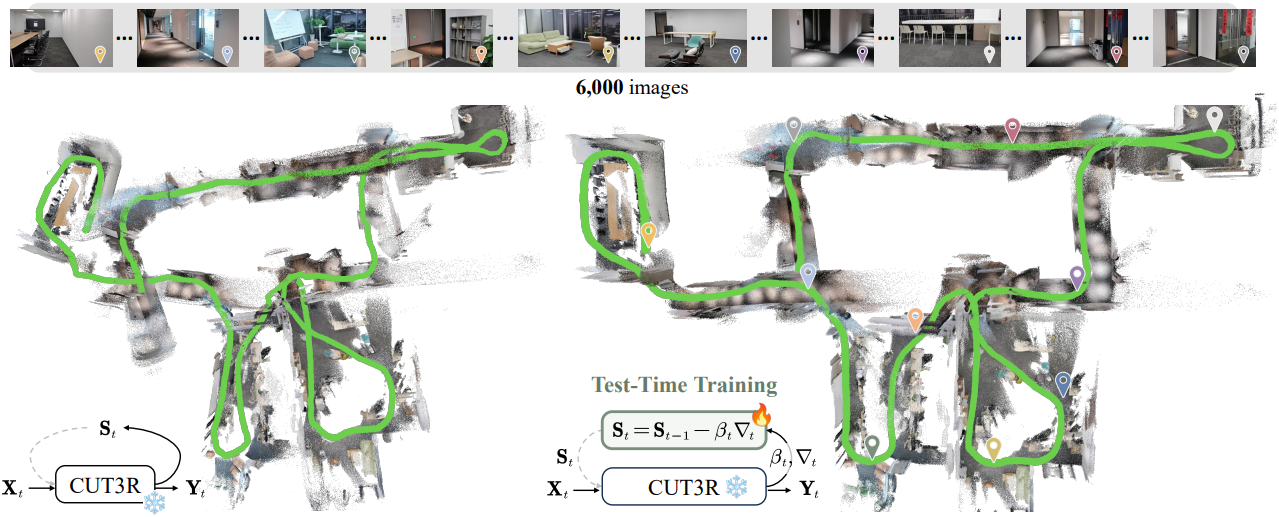
Introduction

3D reconstruction foundation model은 입력 RGB 이미지 세트로부터 카메라 포즈와 장면 표현을 예측하는 것을 목표로 한다. 실제로는 임의의 개수의 이미지를 처리해야 하며, 최근의 feedforward 방식(ex. VGGT, Point3R)은 높은 메모리 소비라는 문제점을 안고 있다. 특히, RNN 기반 설계에서 일정한 메모리 사용량을 달성하는 것은 CUT3R뿐이다. 그러나 CUT3R는 대부분의 64프레임 시퀀스를 학습하기 때문에 긴 시퀀스로 일반화하는 데 실패한다.

최근 RNN은 언어 task에서 Transformer와 동등한 성능을 보여주었다. Recurrent 아키텍처는 history context를 고정 길이의 memory state로 압축하며, 각 출력은 현재 state와 입력 관측값에만 의존한다. 이 recurrent 메커니즘은 선형 계산 복잡도를 가진 긴 시퀀스를 효율적으로 처리하고, state를 rollout하여 더 긴 시퀀스로 확장할 수 있다는 장점이 있다. 그러나 이러한 이점은 종종 상당한 성능 저하를 초래하며, 특히 시퀀스 길이가 학습 컨텍스트를 초과할 때 더욱 그렇다.

본 논문에서는 test-time training (TTT)의 관점에서 recurrent 3D reconstruction 모델의 state 업데이트 규칙을 다시 살펴보고, 다양한 시퀀스 길이에 걸쳐 일반화하는 능력을 방해하는 요인을 체계적으로 조사하였다. 특히, 저자들은 recurrent model이 state overfitting으로 인해 길이 일반화에 어려움을 겪는다는 최근 연구 결과에 영감을 받아, state 업데이트를 TTT 스타일의 온라인 학습 프로세스로 재구성하였다.

과거 정보는 온라인으로 state로 압축된다. 저자들은 state를 입력 컨텍스트 토큰에서 test-time에 학습된 가중치로 해석하였다. 이러한 관점은 state overfitting에 대한 원칙적인 이해를 제공한다. 즉, 긴 컨텍스트에서의 연상적 기억(associative recall)과, 망각과 학습 간 균형을 맞추기 위한 적응형 learning rate 기반의 gradient 업데이트를 결합하면, 길이 일반화 능력을 상당히 향상시킬 수 있음을 시사한다.

또한, 저자들은 CUT3R가 TTT 메커니즘으로 해석될 수 있는 반면, 학습 중 시퀀스 길이를 단순히 늘리는 것은 FLOP 활용도가 매우 낮음을 발견했다. 따라서 CUT3R에서의 온라인 associative recall을 위하여, closed-form state transition으로 유도된 TTT3R이라는 간단하면서도 효과적인 inference-time state 업데이트 규칙을 제안하였다. 이 transition은 test-time에 state를 업데이트하는 데 필요한 learning rate를 명시적으로 정의하여 길이 일반화를 가능하게 한다. 본 접근법은 내부 신뢰도 신호를 활용하여 저품질 state 업데이트를 선택적으로 억제한다. 이를 통해 fine-tuning이나 추가 파라미터 없이도 catastrophic forgetting을 완화하는 안정적이고 학습이 필요 없는 gating 메커니즘을 제공한다.

Method

본 방법은 온라인으로 들어오는 연속적인 이미지 스트림을 처리한다. 각 들어온 이미지 \(\textbf{I}_t \in \mathbb{R}^{W \times H \times 3}\)에 대해, 카메라 포즈 \(\textbf{T}_t \in \mathbb{R}^{3 \times 4}\), 카메라 intrinsic \(\textbf{C}_t \in \mathbb{R}^{3 \times 3}\), 그리고 포인트 클라우드 \(\textbf{P}_t \in \mathbb{R}^{W \times H \times 3}\)을 실시간으로 추정하는 것을 목표로 한다.

1. Sequence Modeling for Pointmap Regression

입력 이미지 \(\textbf{I}_t\)는 DINO나 CroCo와 같은 이미지 tokenizer를 통해 이미지 토큰 세트 \(\textbf{X}_t\)로 patchify된다. 이미지 토큰 \(\textbf{X}_t\)는 새 정보를 사용하여 이전 state \(\textbf{S}_{t-1}\)을 현재 state \(\textbf{S}_t\)로 업데이트한다. 그런 다음 모델은 출력 토큰 \(\textbf{Y}_t\)를 읽어서 업데이트된 state \(\textbf{S}_t\)에 저장된 정보를 검색한다. \(\textbf{Y}_t\)는 pixel shuffle이나 DPT head를 통과한 후, linear layer를 통과하는 de-tokenizer를 통해 해당 픽셀 정렬된 3D pointmap이 된다.

\[\begin{aligned} \textbf{X}_t &= \textrm{Tokenize} (\textbf{I}_t) \in \mathbb{R}^{(h \times w) \times c} \\ \textbf{S}_t &= \textrm{Update} (\textbf{S}_{t-1}, \textbf{X}_t) \\ \textbf{Y}_t &= \textrm{Read} (\textbf{S}_t, \textbf{X}_t) \in \mathbb{R}^{(h \times w) \times c} \\ \textbf{P}_t &= \textrm{De-tokenize} (\textbf{Y}_t) \in \mathbb{R}^{H \times W \times 3} \end{aligned}\]

카메라 포즈 \(\textbf{T}_t\)와 카메라 intrinsic \(\textbf{C}_t\)는 PnP와 Weiszfeld 알고리즘을 사용하여 픽셀 정렬된 3D pointmap에서 계산하거나 MLP 또는 trunk attention layer를 통해 이미지 토큰 \(\textbf{X}_t\)에서 예측될 수 있다.

여기서 업데이트 및 읽기 연산은 여러 방법 간의 핵심적인 차이점으로 작용한다. 이 방법들은 full attention 기반 모델과 RNN 기반 모델, 두 가지 카테고리로 나뉘며, 각 카테고리는 업데이트 규칙에 특화된 설계를 도입한다.

Fast3R나 VGGT와 같은 full attention 기반 방법의 경우 모든 프레임은 글로벌 self-attention을 통해 상호 작용한다. 이는 증가하는 state 길이를 갖는 점진적인 state concatenation으로 해석될 수 있다.

\[\begin{equation} \textrm{Update} (\textbf{S}_{t-1}, \textbf{X}_t) = \textbf{S}_{t-1}.\textrm{append}(\textbf{K}_{\textbf{X}_t}, \textbf{V}_{\textbf{X}_t}) \\ \textrm{Read} (\textbf{S}_t, \textbf{X}_t) = \textrm{X}_t + \textrm{softmax}(\textbf{Q}_{\textbf{X}_t} \textbf{K}_{\textbf{S}_t}^\top) \textbf{V}_{\textbf{S}_t} \\ \textrm{where} \quad \textbf{S}_{t-1} = [(\textbf{K}_{\textbf{X}_1}, \textbf{V}_{\textbf{X}_1}), \ldots, (\textbf{K}_{\textbf{X}_{t-1}}, \textbf{V}_{\textbf{X}_{t-1}})], \; \textbf{K}_{\textbf{S}_t} = \textrm{concat}[\textbf{K}_{\textbf{X}_1}, \ldots, \textbf{K}_{\textbf{X}_t}], \; \textbf{V}_{\textbf{S}_t} = \textrm{concat}[\textbf{V}_{\textbf{X}_1}, \ldots, \textbf{V}_{\textbf{X}_t}] \end{equation}\]

각 key-value 쌍 \((\textbf{K}_{\textbf{X}_t}, \textbf{V}_{\textbf{X}_t})\)와 query \(\textbf{Q}_{\textbf{X}_t}\)는 linear layer를 통해 입력 토큰 \(\textbf{X}_t\)에서 변환된다.

이 모델링에는 모든 출력 토큰 \(\textbf{Y}_1, \ldots, \textbf{Y}_t\)가 \(\textbf{X}_t\)를 받을 때 업데이트되어야 하므로 $\mathcal{O} (t^2)$ 컴퓨팅 복잡도가 필요하다. 스트리밍 입력을 효율적으로 처리하기 위해 StreamVGGT는 causal attention 아키텍처를 사용하여 스트리밍 데이터의 인과적인 특성을 모델링하였다. 이는 계산 비용을 $\mathcal{O}(t)$로 줄였지만, full attention 기반 방법들과 마찬가지로 뷰 수가 증가함에 따라 메모리 소비가 증가한다.

CUT3R와 같은 RNN 기반 방법의 경우, 들어오는 각 프레임은 1대1 cross-attention을 통해 상태와 상호 작용하여 고정 길이의 state를 허용한다.

\[\begin{equation} \textrm{Update} (\textbf{S}_{t-1}, \textbf{X}_t) = \textbf{S}_{t-1} + \textrm{softmax}(\textbf{Q}_{\textbf{S}_{t-1}} \textbf{K}_{\textbf{X}_t}^\top) \textbf{V}_{\textbf{X}_t} \end{equation}\]

채널 차원이 $c$이고 $n$개의 토큰으로 구성된 state \(\textbf{S}_{t-1} \in \mathbb{R}^{n \times c}\)는 장면을 일정한 길이로 인코딩한다. 이 재귀적 공식은 계산 복잡도를 $\mathcal{O}(1)$로 효과적으로 줄이고 inference 메모리 사용량도 $\mathcal{O}(1)$로 일정하게 유지하지만, 입력 뷰 수가 증가함에 따라 catastrophic forgetting 현상이 발생하고 성능이 크게 저하된다.

2. Revisit RNN-based Reconstruction through TTT

Test-Time Training (TTT)은 학습과 inference 과정에서 동적으로 컨텍스트를 포착하기 위해 업데이트되는 빠르게 적응 가능한 state인 fast weight를 도입한다. 반면, slow weight, 즉 모델 파라미터는 inference 과정에서 고정된 상태를 유지한다. TTT는 state를 고정 길이의 fast weight \(\textbf{S}_{t-1} \in \mathbb{R}^{n \times c}\)로 표현하고 gradient descent를 통해 업데이트한다.

\[\begin{equation} \textrm{Update} (\textbf{S}_{t-1}, \textbf{X}_t) = \textbf{S}_{t-1} - \beta_t \nabla (\textbf{S}_{t-1}, \textbf{X}_t) \end{equation}\]

(\(\beta_t\)는 learning rate)

직관적으로, 이 온라인 학습 과정은 현재 관측치의 KV-cache를 고정 길이의 메모리, 즉 state로 최대한 정확하게 인코딩한다.

일반적으로 \(\beta_t\) 다음과 같이 표현된다.

1. 학습 가능한 스칼라 파라미터 $\beta \in \mathbb{R}$
2. 입력의 dependent한 스칼라 함수 \(\beta_t = \sigma (\ell_\beta (\textbf{X}_t)) \in \mathbb{R}\)
3. 토큰별 함수 \(\beta_t = \sigma (\ell_\beta (\textbf{X}_t)) \in \mathbb{R}^{n \times 1}\)

CUT3R의 업데이트 연산은 \(\beta_t = 1\)인 TTT로 생각할 수 있다.

\[\begin{equation} \textbf{S}_{t-1} + \textrm{softmax}(\textbf{Q}_{\textbf{S}_{t-1}} \textbf{K}_{\textbf{X}_t}^\top) \textbf{V}_{\textbf{X}_t} = \textbf{S}_{t-1} - \beta_t \nabla (\textbf{S}_{t-1}, \textbf{X}_t) \\ \Rightarrow \quad \beta_t = 1, \quad \nabla (\textbf{S}_{t-1}, \textbf{X}_t) = -\textrm{softmax}(\textbf{Q}_{\textbf{S}_{t-1}} \textbf{K}_{\textbf{X}_t}^\top) \textbf{V}_{\textbf{X}_t} \end{equation}\]

그러나 softmax 연산은 모델이 최신 관측값에 완전히 적응하도록 강제하기 때문에 CUT3R가 과거 정보를 유지하는 것과 새로운 입력을 통합하는 것 사이의 균형을 맞추는 데 한계가 있다. 특히, softmax 가중치는 관측값 토큰 차원을 따라 합이 1.0이 되도록 정규화되기 때문에, 모델은 항상 과거 상태 \(\textbf{S}_{t-1}\)보다 새로운 정보 \(\textbf{X}_t\)를 우선시하여 catastrophic forgetting을 초래한다.

3. Confidence-Guided State Update Rule

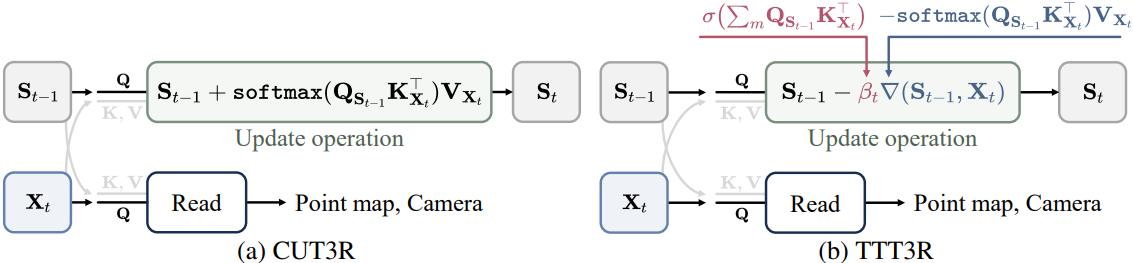
저자들의 핵심 아이디어는 메모리와 관측값 간의 정렬 신뢰도를 활용하여 state 업데이트를 유도하는 것이며, 이 신뢰도는 TTT에서 learning rate 역할을 한다.

Cross-attention \(\textbf{Q}_{\textbf{S}_{t-1}} \textbf{K}_{\textbf{X}_t}^\top\)은 이미지의 공간 차원 \(m = \{1, \ldots, h\} \times \{1, \ldots, w\}\)에 따라 정보를 $n$개의 state 토큰으로 집계한다. 이 과정을 통해 각 state 토큰에 대한 정규화된 attention 가중치가 생성되고, 이 가중치는 value \(\textbf{V}_{\textbf{X}_t}\)에 대한 가중 합을 계산하는 데 사용된다.

저자들은 catastrophic forgetting 문제를 해결하기 위해, 원래의 attention 공식을 유지하지만 state의 query \(\textbf{Q}_{\textbf{S}_{t-1}}\)과 관측값의 key \(\textbf{K}_{\textbf{X}_t}\) 간의 정렬 신뢰도에서 파생된 토큰별 learning rate \(\beta_t \in \mathbb{R}^{n \times 1}\)를 도입하였다.

\[\begin{equation} \beta_t = \sigma (\sum_m \textbf{Q}_{\textbf{S}_{t-1}} \textbf{K}_{\textbf{X}_t}^\top) \end{equation}\]

이 learning rate는 gated attention에서 soft gate 역할을 할 수 있으며, attention에서 출력에 통합하면 더 나은 long-context extrapolation을 가능하게 한다. 결과적으로, 완전한 state 업데이트 규칙은 다음과 같다.

\[\begin{aligned} \textrm{Update} (\textbf{S}_{t-1}, \textbf{X}_t) &= \textbf{S}_{t-1} - \beta_t \nabla (\textbf{S}_{t-1}, \textbf{X}_t) \\ &= \textbf{S}_{t-1} + \sigma (\sum_m \textbf{Q}_{\textbf{S}_{t-1}} \textbf{K}_{\textbf{X}_t}^\top) \textrm{softmax} (\textbf{Q}_{\textbf{S}_{t-1}} \textbf{K}_{\textbf{X}_t}^\top) \textbf{V}_{\textbf{X}_t} \end{aligned}\]

State 업데이트의 정렬 신뢰도가 높을수록 일반적으로 state와 관측치 간의 일치도가 더 높고 불확실성이 낮아져 업데이트 step이 더 커진다. 토큰 수준의 통계를 통합함으로써 저품질의 state에 대한 업데이트가 억제되고 성능을 향상된다. 또한, 이 공식을 사용하면 CUT3R에 대한 학습이 필요 없는 plug-and-play 방식의 개입이 가능하며, 추가적인 fine-tuning 없이 다운스트림 task에 직접 적용할 수 있다.

Experiments

1. Camera Pose Estimation

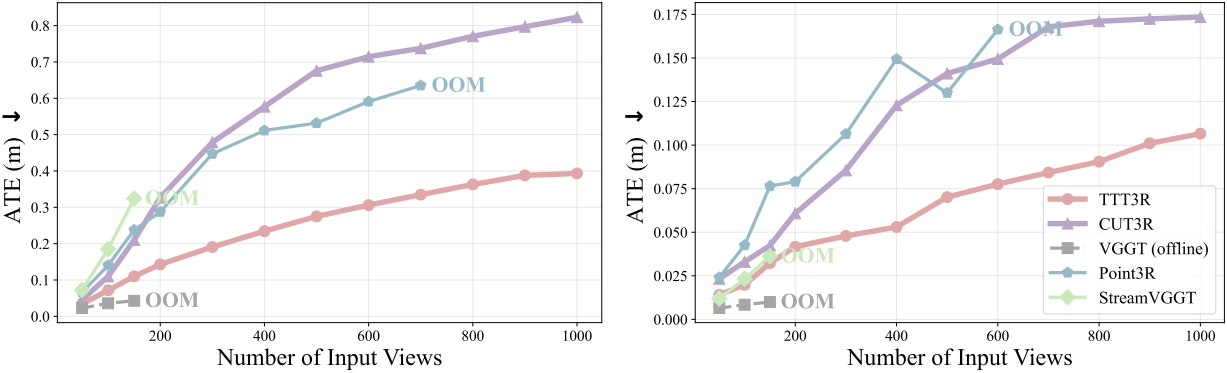
다음은 (왼쪽) ScanNet과 (오른쪽) TUM-D에서의 카메라 포즈를 비교한 결과이다.

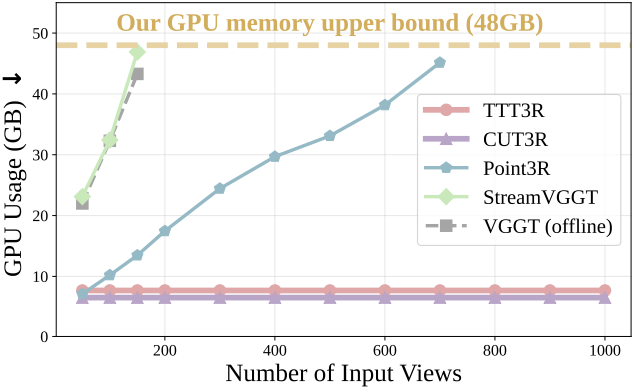
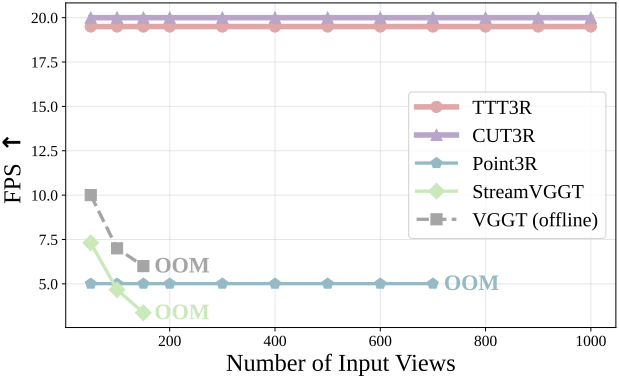
다음은 ScanNet에서의 런타임을 비교한 결과이다.

2. Video Depth Estimation

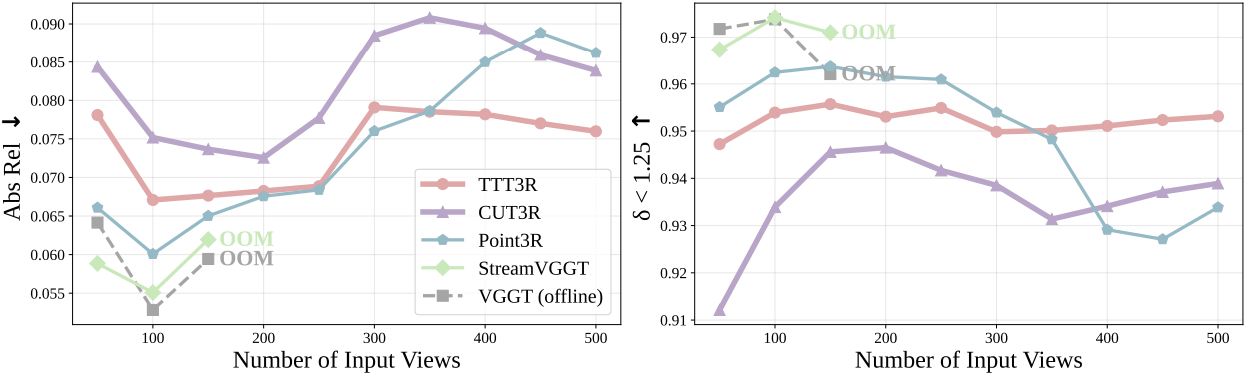
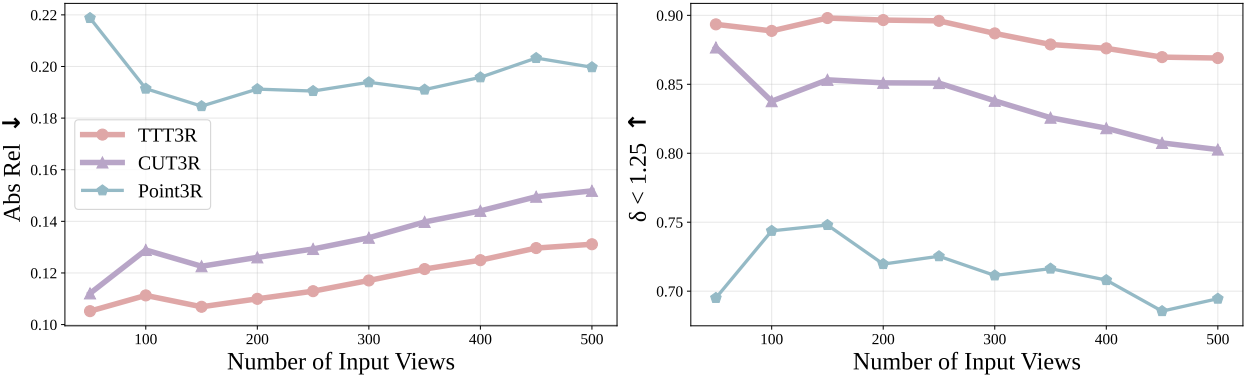
다음은 (위) Bonn 데이터셋에서의 relative depth와 (아래) KITTI에서의 metric depth를 비교한 결과이다.

3. 3D Reconstruction

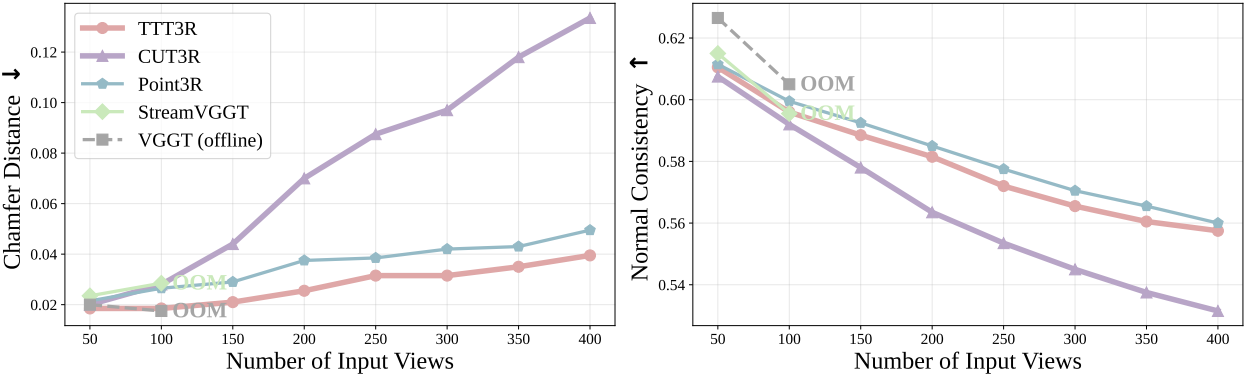
다음은 7-scene에서의 3D reconstruction을 비교한 결과이다.

다음은 3D reconstruction 결과를 비교한 예시들이다.