Diffusion은 신이고 GPT는 무적이다

arXiv 2025. [Paper] [Github]
Yuxin Zuo, Kaiyan Zhang, Li Sheng, Shang Qu, Ganqu Cui, Xuekai Zhu, Haozhan Li, Yuchen Zhang, Xinwei Long, Ermo Hua, Biqing Qi, Youbang Sun, Zhiyuan Ma, Lifan Yuan, Ning Ding, Bowen Zhou
Tsinghua University | Shanghai AI Lab
22 Apr 2025

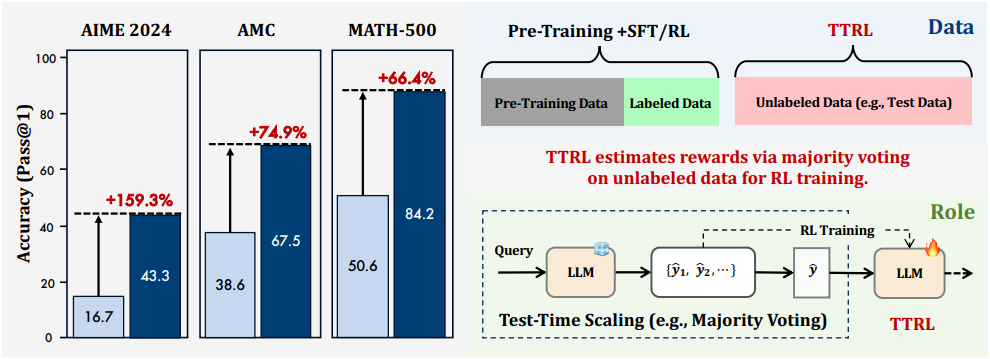
Introduction

본 논문은 강화학습(RL)을 통해 test-time에서 모델을 업데이트함으로써, 이전에 본 적 없는 데이터에 대한 일반화 성능을 향상시키는 것을 목표로 한다. 하지만 test-time에서 RL에 필요한 reward를 어떻게 얻을 것인지가 문제이다. 대부분의 기존 RL 방법들은 여전히 레이블이 있는 데이터에 강하게 의존하고 있으며, 이는 확장성에 큰 제약을 준다. 현실의 task들이 점점 더 복잡해지고 방대해짐에 따라, 강화학습을 위한 대규모 레이블링은 점점 더 비현실적이 되며, 이는 SOTA 모델의 지속적인 개선에 있어 중대한 장애물로 작용한다.

본 논문은 Test-Time Reinforcement Learning (TTRL)을 소개한다. TTRL은 test-time에서의 학습을 강화학습을 통해 수행한다. 이 방식은 롤아웃 단계에서 반복적인 샘플링 전략을 활용하여 레이블을 정확히 추정하고 규칙 기반 reward를 계산함으로써, 레이블이 없는 데이터에 대해 강화학습을 가능하게 한다. 효과적인 다수결 reward를 도입함으로써, TTRL은 정답 레이블 없이도 효율적이고 안정적인 강화학습을 지원한다. 본질적으로, TTRL은 모델이 자신의 경험을 생성하고, reward를 추정하며, 시간이 지남에 따라 성능을 향상시킬 수 있도록 만든다.

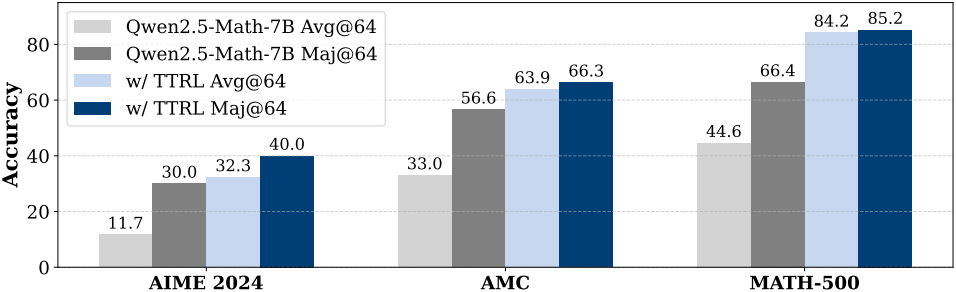
TTRL을 Qwen2.5-Math-7B에 적용한 결과, AIME 2024에서 211% 향상되었으며 (12.9 $\rightarrow$ 40.2), AIME 2024, AMC, MATH-500, GPQA에 대하여 전체 평균 76%의 향상을 보였다. 이러한 향상은 레이블이 있는 학습 데이터 없이 자체 진화를 통해 달성되었으며, 다른 task로 일반화되었다. TTRL은 pass@1 성능을 향상시킬 뿐만 아니라, 다수결을 통해 test-time scaling도 향상시킨다. 또한, TTRL은 다양한 규모와 유형의 모델에서 효과적이며, 기존 RL 알고리즘과 통합될 수 있다. TTRL은 주석에 대한 의존도를 크게 줄여 지속적인 학습을 가능하게 하고 RL을 대규모 unsupervised training으로 확장할 수 있는 잠재력을 보여준다.

Method


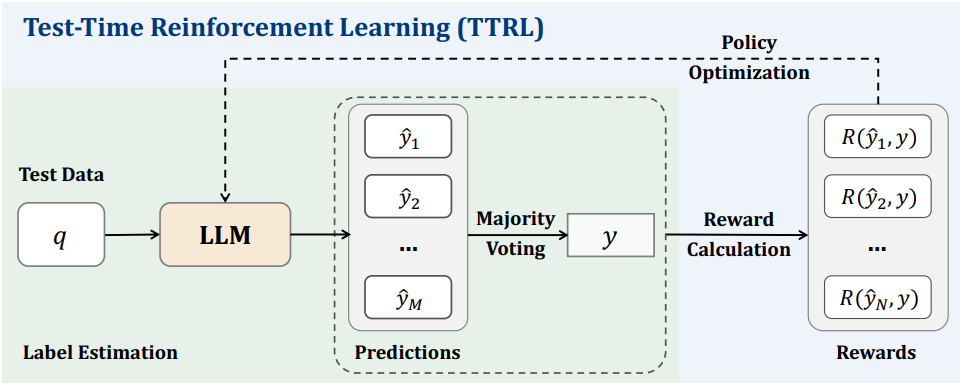
프롬프트 $x$로 표현된 state가 주어지면, 모델은 policy \(\pi_\theta (y \vert x)\)에서 샘플링된 출력 $y$를 생성한다. GT 레이블이 없는 reward 신호를 생성하기 위해, 반복적인 샘플링을 통해 모델에서 여러 후보 출력 \(\{y_1, \ldots, y_N\}\)을 생성한다. 다른 집계 방법 (ex. 다수결)을 통해 합의된 출력 $y^\ast$가 도출되며, 이는 최적 action 역할을 한다. 그러면 environment은 샘플링된 action $y$와 합의 행동 $y^\ast$의 일치도에 따라 reward $r(y, y^\ast)$를 제공한다. RL의 목표는 reward 기대값을 최대화하는 것이다.

\[\begin{equation} \max_\theta \mathbb{E}_{y \sim \pi_\theta (\cdot \vert x)} [r (y, y^\ast)] \end{equation}\]

파라미터 $\theta$는 gradient ascent를 통해 업데이트된다.

\[\begin{equation} \theta \leftarrow \theta + \eta \nabla_\theta \mathbb{E}_{y \sim \pi_\theta (\cdot \vert x)} [r (y, y^\ast)] \end{equation}\]

($\eta$는 learning rate)

이 접근법은 모델이 inference 과정에서 적응할 수 있도록 하여, 레이블 없이도 분포가 이동된 입력에 대한 성능을 효과적으로 향상시킬 수 있도록 한다.

Majority Voting Reward Function

다수결 reward는 다수결을 통해 레이블을 먼저 추정하여 결정된다. 이 추정된 레이블은 최종 reward로 사용되는 rule-based reward를 계산하는 데 사용된다. 질문 $x$가 주어지면, 먼저 $x$를 LLM에 입력하여 출력 집합을 생성한다. 그런 다음, 이러한 출력을 처리하여 해당 예측 답변 \(P = \{\hat{y}_i\}_{i=1}^N\)을 얻는다. 그런 다음, 다수결로 $P$에서 가장 자주 발생하는 예측인 $y$를 얻는다. 다수결로 선택된 예측 $y$는 rule-based reward를 계산하는 레이블로 사용된다. Reward function은 다음과 같다.

\[\begin{equation} R (\hat{y}_i, y) = \begin{cases} 1 & \textrm{if} \; \hat{y}_i = y \\ 0 & \textrm{otherwise} \end{cases} \end{equation}\]

Experiments

1. Main Results

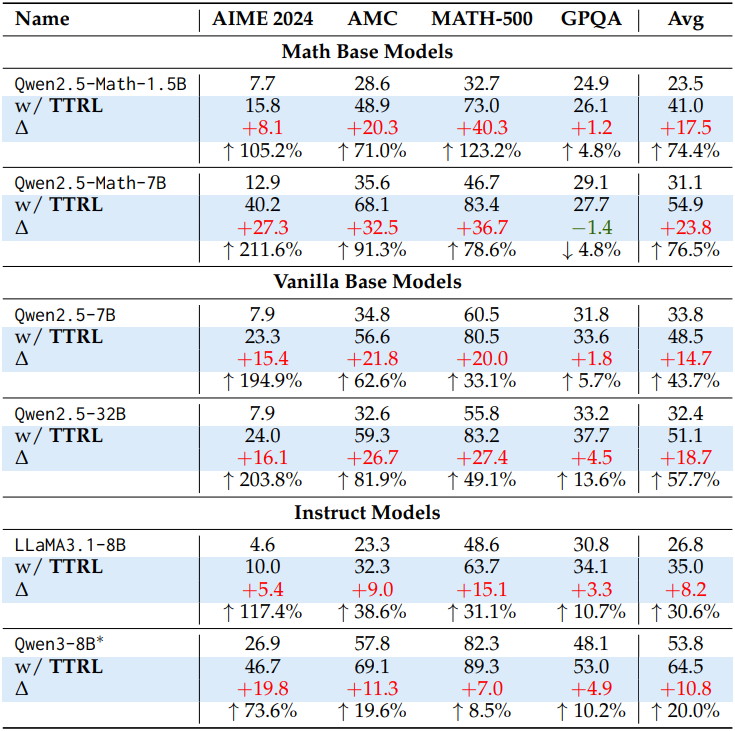
다음은 다양한 모델에 대한 TTRL 적용 전후의 성능을 비교한 결과이다.


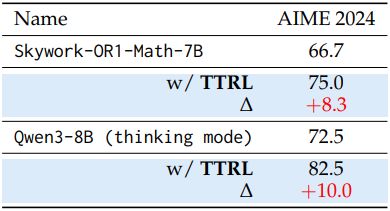
다음은 추론 모델에 대한 TTRL 적용 전후의 성능을 비교한 결과이다.


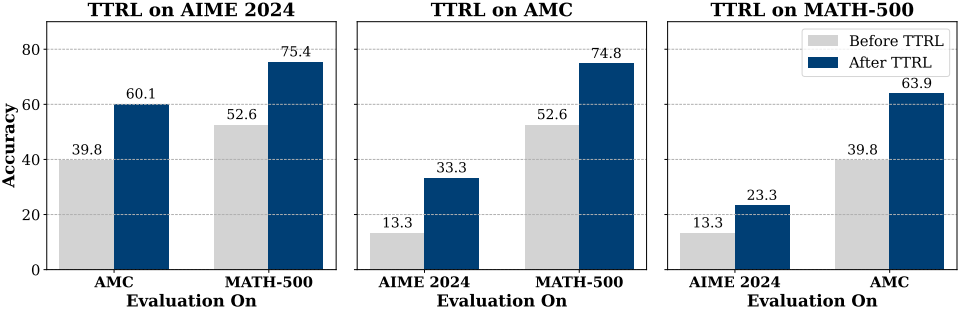
다음은 TTRL 적용 전후의 out-of-distribution 성능을 비교한 결과이다.


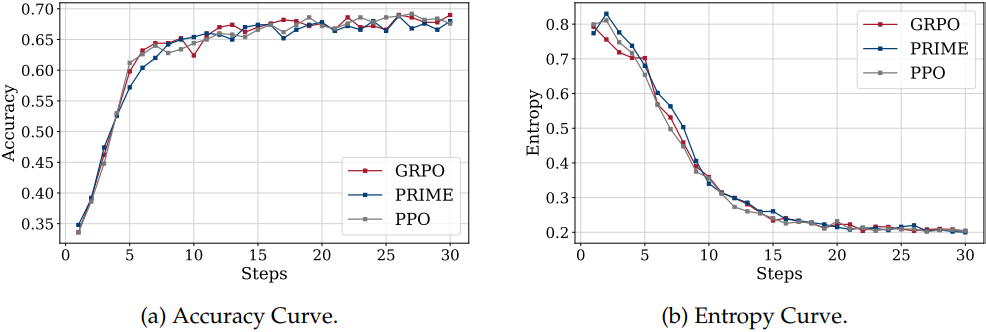
다음은 다른 RL 알고리즘과 TTRL을 함께 적용한 결과이다.

2. Analysis and Discussions

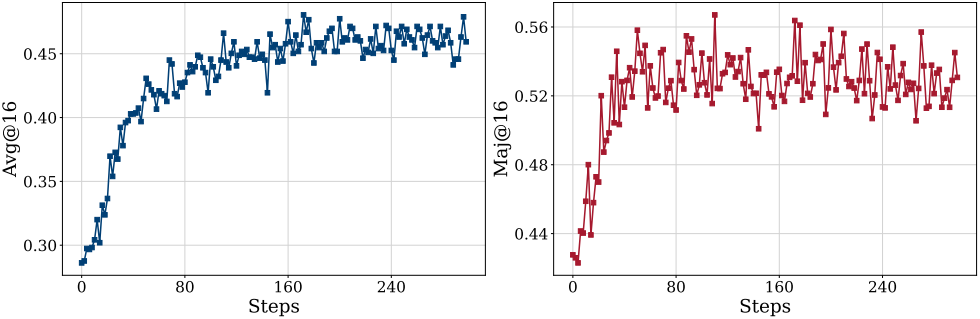
다음은 학습 진행에 따른 평균 점수와 다수결 점수를 나타낸 그래프이다.


다음은 TTRL 전후의 다수결 투표 성능을 비교한 결과이다.


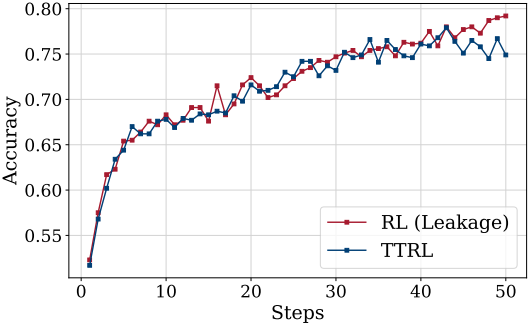
다음은 RL (leakage)와 TTRL을 비교한 그래프이다. RL (leakage)는 테스트 데이터에 직접 RL을 수행하는 것이며, TTRL의 자연스러운 상한이다.


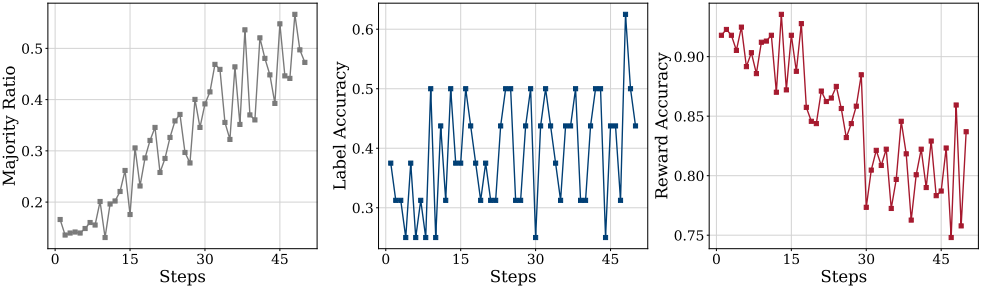
다음은 다수결 비율, 레이블 정확도, reward 정확도를 학습이 진행됨에 따라 나타낸 그래프이다.


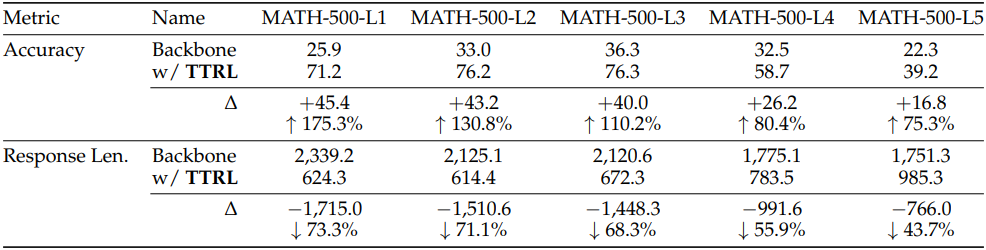
다음은 MATH-500의 난이도에 따른 성능 변화를 비교한 결과이다.

You may also enjoy