[논문리뷰] TSRFormer: Table Structure Recognition with Transformers
ACM MultiMedia 2022. [Paper]
Weihong Lin, Zheng Sun, Chixiang Ma, Mingze Li, Jiawei Wang, Lei Sun, Qiang Huo
Microsoft Research Asia | University of Chinese Academy of Sciences & CASIA | University of Science and Technology of China | Shanghai Jiao Tong University
9 Aug 2022
Introduction
디지털 전환 추세로 인해 자동 테이블 구조 인식 (table structure recognition, TSR)은 중요한 연구 분야가 되었으며 많은 연구자의 관심을 끌었다. TSR은 셀 박스의 좌표와 행/열 스패닝 정보를 추출하여 테이블 이미지에서 테이블의 셀룰러 구조를 인식하는 것을 목표로 한다. 이 task는 테이블이 복잡한 구조, 다양한 스타일, 내용을 가질 수 있고 이미지 캡처 프로세스 중에 기하학적으로 왜곡되거나 구부러질 수 있기 때문에 매우 어렵다.
최근 딥 러닝 기반 TSR 방법은 복잡한 구조와 다양한 스타일을 가진 왜곡되지 않은 테이블을 인식하는 데 인상적인 발전을 이루었다. 그러나 Cycle-CenterNet을 제외한 이러한 방법은 카메라 촬영 이미지에 자주 나타나는 기하학적으로 왜곡되거나 구부러진 테이블에 직접 적용할 수 없다. Cycle-CenterNet은 복잡한 장면에서 왜곡된 테두리가 있는 테이블의 구조를 구문 분석하는 효과적인 접근 방식을 제안하고 WTW 데이터셋에서 유망한 결과를 얻었지만 테두리 없는 테이블을 고려하지 않았다. 따라서 다양한 기하학적으로 왜곡된 테이블의 구조를 인식하는 더 어려운 문제는 여전히 조사가 부족하다.
본 논문에서는 경계가 있는 왜곡 테이블과 경계가 없는 왜곡 테이블의 구조를 robust하게 인식하기 위해 TSRFormer라는 새로운 TSR 접근 방식을 제안한다. TSRFormer에는 두 가지 효과적인 구성 요소가 포함되어 있다.
- 입력 테이블 이미지에서 선형 및 곡선 행/열 분리선을 직접 예측하는 2단계 DETR 기반 분리 회귀 모듈
- 행과 열 구분자가 교차하여 생성된 인접 셀을 병합하여 스패닝 셀을 복구하는 relation network 기반 셀 병합 모듈
이전의 split-and-merge 기반 접근 방식과 달리 이미지 분할 문제 대신 구분선 회귀 문제로 구분선 예측을 공식화하고 Separator REgression TRansformer (SepRETR)이라는 새로운 구분선 예측 접근 방식을 제안하여 테이블 이미지에서 직접 구분선을 예측한다. 이러한 방식으로 휴리스틱한 mask-to-line 모듈을 제거하고 왜곡된 테이블에 대해 더 robust해질 수 있다. 특히, SepRETR은 먼저 각 행/열 구분자에 대해 하나의 기준점을 예측한 다음 이러한 기준점의 feature들을 개체 쿼리로 가져와 DETR 디코더에 공급하여 해당 구분선의 좌표를 직접 회귀한다. 본 논문은 2단계 DETR 프레임워크가 분리선 예측에 대해 효율적이고 효과적으로 작동하도록 하기 위해 두 가지 추가 개선 사항을 제안하였다.
- DETR의 느린 수렴 문제를 해결하기 위한 prior 강화 매칭 전략
- 낮은 계산 비용으로 높은 localization 정확도를 달성할 수 있도록 고해상도 convolution feature map에서 직접 feature를 샘플링하는 새로운 cross-attention 모듈
이러한 새로운 기술을 통해 TSRFormer는 여러 TSR 벤치마크에서 SOTA 성능을 달성했다. 또한 복잡한 구조, 경계선 없는 셀, 큰 빈 공간, 빈 셀 또는 스패닝 셀, 왜곡되거나 구부러진 모양이 있는 테이블에 대한 접근 방식의 robustness를 보다 까다로운 실제 내부 데이터셋에서 입증했다.
Methodology
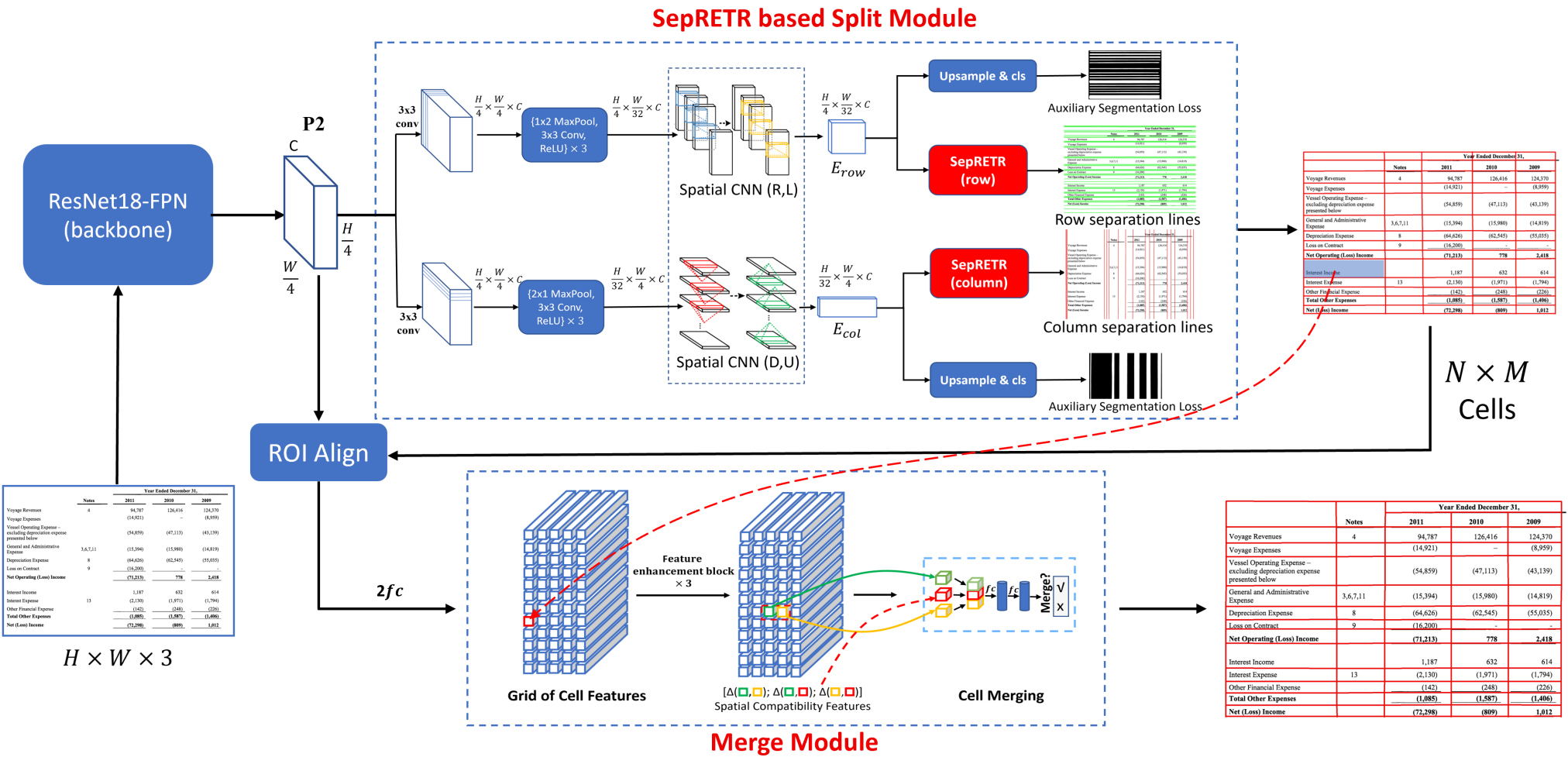
위 그림과 같이 TSRFormer에는 두 가지 주요 구성 요소가 포함되어 있다.
- 각 입력 테이블 이미지에서 모든 행/열 구분선을 예측하는 SepRETR 기반 분할 모듈
- 스패닝 셀을 복구하기 위한 relation network 기반 셀 병합 모듈
이 두 모듈은 ResNet-FPN backbone에서 생성된 공유 convolution feature map $P_2$에 연결된다.
1. SepRETR based Split Module
분할 모듈에서 두 개의 병렬 분기가 공유 feature map $P_2$에 연결되어 각각 행/열 구분자를 예측한다. 각 분기는 세 가지 모듈로 구성된다.
- 컨텍스트 향상 feature map을 생성하는 feature enhancement 모듈
- SepRETR 기반 분리선 예측 모듈
- 보조 분리선 분할 모듈
Feature enhancement
위 그림과 같이 $P_2$ 뒤에 3$\times$3 convolution layer와 3개의 반복된 다운샘플링 블록을 추가하여 순차적으로 다운샘플링된 feature map
\[\begin{equation} P'_2 \in \mathbb{R}^{\frac{H}{4} \times \frac{W}{32} \times C} \end{equation}\]를 먼저 생성한다. 각 다운샘플링 블록은 1$\times$2 max-pooling layer, 3$\times$3 convolution layer, ReLU의 시퀀스로 구성된다. 다음으로 2개의 계단식 spatial CNN (SCNN) 모듈을 \(P'_2\)에 연결하여 전체 feature map에 대해 오른쪽 및 왼쪽 방향으로 컨텍스트 정보를 전파하여 feature 표현 능력을 더욱 향상시킨다. 오른쪽 방향을 예로 들면, SCNN 모듈은 \(P'_2\)를 폭 방향으로 $\frac{W}{32}$개의 슬라이스로 분할하고 정보를 왼쪽 슬라이스에서 오른쪽 슬라이스로 전파한다. 각 슬라이스에 대해 먼저 커널 크기가 9$\times$1인 convolution layer로 전송된 다음 element-wise addition을 통해 다음 슬라이스와 병합된다. SCNN 모듈의 도움으로 출력 컨텍스트 향상 feature map $E_\textrm{row}$의 각 픽셀은 더 나은 표현 능력을 위해 양쪽의 구조 정보를 활용할 수 있다.
SepRETR based separation line prediction
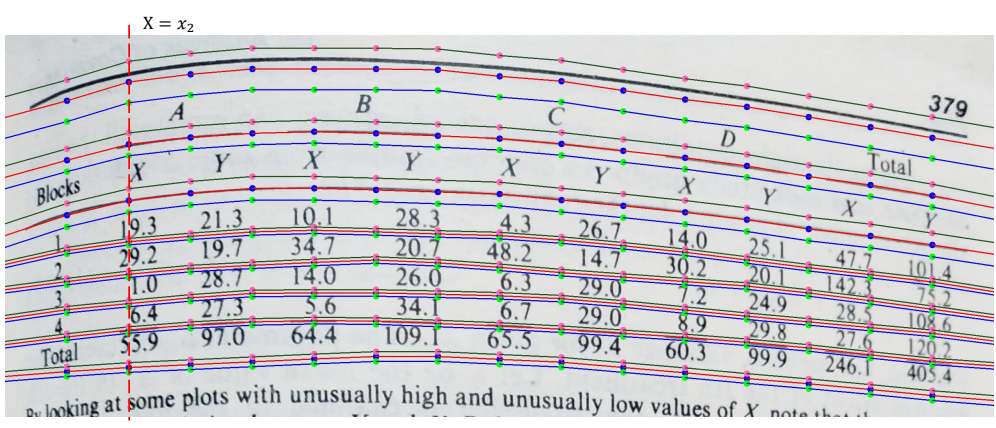
위 그림과 같이 세 개의 평행한 곡선을 사용하여 각 행 구분자의 상단 경계선, 중심선 및 하단 경계선을 각각 나타낸다. 각 곡선은 $K = 15$개의 포인트로 표시되며 $x$ 좌표는 각각 $x_1, \cdots, x_K$로 설정된다. 각 행 구분자에 대해 포인트의 $y$ 좌표 $3K$개는 SepRETR 모델에서 직접 예측한다. 여기에서 $i$번째 $x$ 좌표에 대해
로 설정한다. $y$ 좌표의 경우 위 식에서 $W$를 $H$로 바꾸기만 하면 된다.
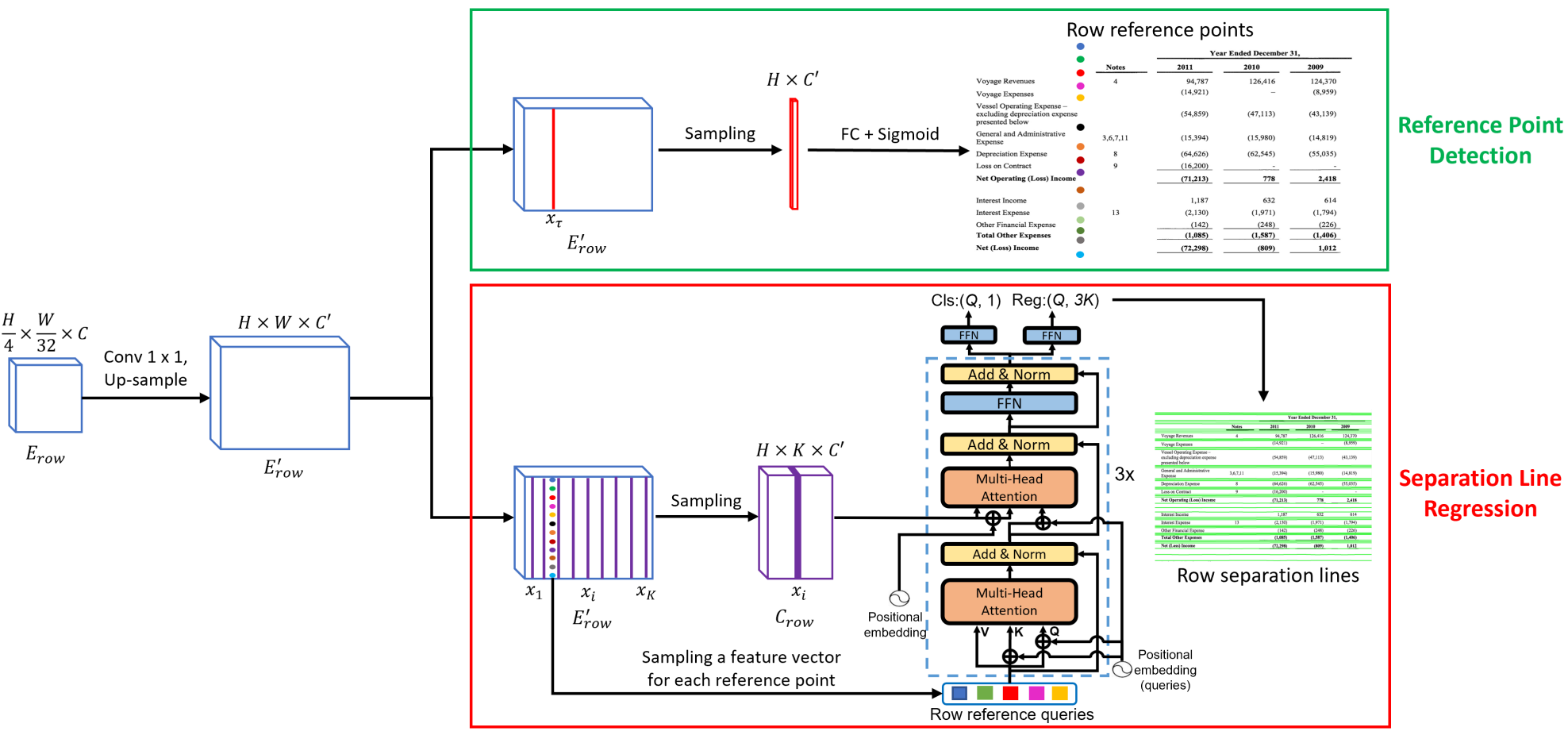
위 그림과 같이 SepRETR에는 기준점 감지 모듈과 분리선 회귀를 위한 DETR 디코더의 두 가지 모듈이 포함되어 있다. 기준점 감지 모듈은 먼저 향상된 feature map $E_\textrm{row}$에서 각 행 구분자에 대한 기준점을 예측하려고 시도한다. 감지된 기준점의 feature는 개체 쿼리로 간주되어 DETR 디코더에 입력되어 각 쿼리에 대한 향상된 임베딩을 생성한다. 이러한 향상된 쿼리 임베딩은 피드포워드 네트워크에 의해 구분선 좌표와 클래스 레이블로 독립적으로 디코딩된다. 두 모듈 모두
에 1$\times$1 convolution layer와 업샘플링 레이어를 순차적으로 추가하여 생성한 고해상도 공유 feature map에 연결된다.
Reference point detection
이 모듈은 이미지의 너비 방향을 따라 고정된 위치 $x_\tau$에서 각 행 구분자에 대한 기준점을 예측하려고 시도한다. 이를 위해 \(E'_\textrm{row}\)의 $x_\tau$번째 열에 있는 각 픽셀은 sigmoid classifier로 공급되어 기준점이 자신의 위치 $(i, x_\tau)$에 위치할 확률을 추정하기 위한 점수 $p_i$를 예측한다.
모든 실험에서 hyperparameter $x_\tau$를 행 라인 예측의 경우 $\lfloor \frac{W}{4} \rfloor$로 설정하고 열 라인 예측의 경우 $y_\tau$를 $\lfloor \frac{H}{4} \rfloor$로 설정한다. \(E'_\textrm{row}\)의 $x_\tau$번째 열에 있는 각 픽셀의 확률이 주어지면, 중복 기준점을 제거하기 위해 이 열에 7$\times$1 max-pooling 레이어를 사용하여 non-maximal suppression (NMS)을 적용한다. 그런 다음 상위 100개 행 기준점이 선택되고 점수 임계값 0.05로 추가 필터링된다. 나머지 행 기준점은 행 분리선 회귀 모듈에서 DETR 디코더의 개체 쿼리로 사용된다.
Separation line regression
효율성을 위해 CNN backbone에서 출력되는 feature을 향상시키기 위해 transformer 인코더를 사용하지 않는다. 대신, 고해상도 feature map \(E'_\textrm{row}\)의 $x_1$번째 열부터 $x_K$번째 열까지를 concat하여 새로운 다운샘플링된 feature map
\[\begin{equation} C_\textrm{row} \in \mathbb{R}^{H \times K \times C'} \end{equation}\]을 생성한다. 그런 다음 해당 위치에서 \(E'_\textrm{row}\)에서 추출한 행 기준점의 feature는 개체 쿼리로 처리되고 분리선 회귀를 위해 3-layer transformer 디코더에 공급된다. 위치 $(x, y)$의 위치 임베딩은 정규화된 좌표 $\frac{x}{W}$와 $\frac{y}{H}$의 sinusoidal embedding을 concat하여 생성되며 이는 DETR에서와 동일하다. Transformer 디코더에 의해 향상된 후 각 쿼리의 feature는 분류와 회귀를 위해 각각 두 개의 피드포워드 네트워크에 공급된다. 행 구분자 회귀에 대한 $y$ 좌표의 ground-truth는 \(\frac{y_\textrm{gt}}{H}\)로 정규화된다.
Prior-enhanced bipartite matching
입력 이미지에서 일련의 예측과 그에 해당하는 ground-truth 객체가 주어지면 DETR은 Hungarian 알고리즘을 사용하여 시스템 예측에 ground-truth 레이블을 할당했다. 그러나 DETR의 원래 이분 매칭 알고리즘은 학습 단계에서 불안정하다. 즉, 쿼리가 다른 학습 epoch에서 동일한 이미지의 다른 객체와 일치될 수 있어 모델 수렴이 크게 느려진다.
첫 번째 단계에서 감지된 대부분의 기준점은 서로 다른 학습 epoch에서 일관되게 해당 행 구분자의 상단과 하단 경계 사이에 위치하므로 이 사전 정보를 활용하여 각 기준점을 가장 가까운 ground-truth (GT) 구분자와 직접 일치시킨다. 이러한 방식으로 매칭 결과는 학습 중에 안정될 것이다.
특히 각 기준점과 각 GT 구분자 사이의 거리를 측정하여 cost matrix를 생성한다. 기준점이 GT 구분자의 위쪽과 아래쪽 경계 사이에 있는 경우 cost는 이 기준점에서 이 구분자의 GT 기준점까지의 거리로 설정된다. 그렇지 않으면 cost가 무한대로 설정된다. 이 cost matrix를 기반으로 Hungarian 알고리즘을 사용하여 기준점과 GT 구분자 간의 최적의 이분 매칭을 생성한다. 최적의 매칭 결과를 얻은 후 cost가 무한대인 쌍을 추가로 제거하여 불합리한 레이블 할당을 피한다.
Auxiliary separation line segmentation
이 보조 분기는 각 픽셀이 구분자 영역에 있는지 여부를 예측하는 것을 목표로 한다. 이 보조 loss를 계산하기 위한 이진 마스크
\[\begin{equation} M_\textrm{row} \in \mathbb{R}^{H \times W \times 1} \end{equation}\]을 예측하기 위해 \(E_\textrm{row}\) 뒤에 1$\times$1 convolution layer와 sigmoid classifier가 뒤따르는 업 샘플링 연산을 추가한다.
2. Relation Network based Cell Merging
분리선 예측 후 행 라인과 열 라인을 교차하여 셀 그리드를 생성하고 relation network를 사용하여 일부 인접 셀을 병합하여 스패닝 셀을 복구한다. 먼저 RoI Align 알고리즘을 사용하여 각 셀의 boundary box를 기반으로 $P_2$에서 $7 \times 7 \times C$ feature map을 추출한 다음, 각 레이어에 512개의 노드가 있는 2-layer MLP에 공급하여 512차원 feature 벡터를 생성한다.
이러한 셀 feature는 $N$개의 행과 $M$개의 열이 있는 그리드에 배열되어 feature map을 형성할 수 있다. 그런 다음 3개의 반복되는 feature enhancement 블록으로 향상되어 인접한 셀 간의 관계를 예측한다. 각 feature enhancement 블록에는 각각 행 레벨 max-pooling layer, 열 레벨 max-pooling layerm 3$\times$3 convolution layer가 있는 세 개의 병렬 분기가 포함된다. 이 세 분기의 출력 feature map은 함께 concat되고 차원 감소를 위해 1$\times$1 convolution layer를 통과한다.
Relation network에서 인접한 셀의 각 쌍에 대해 해당 feature와 18차원 공간 호환성 feature을 concat한다. 그런 다음 이 feature에 binary classifier를 적용하여 이 두 셀을 병합해야 하는지 여부를 예측한다. Classifier는 각 hidden layer에 512개의 노드가 있는 2-hidden layer MLP와 시그모이드 함수로 구현된다.
3. Loss Function
분할 모듈의 경우 행 구분자 예측의 loss는 \(L_\ast^\textrm{row}\)로 표시하며 열 구분자 예측의 loss는 \(L_\ast^\textrm{col}\)로 표시한다.
Reference point detection
행/열 기준점 감지 모듈을 학습하기 위해 focal loss의 변형을 채택한다.
\[\begin{equation} L_\textrm{ref}^\textrm{row} = - \frac{1}{N_r} \sum_{i=1}^H \begin{cases} (1 - p_i)^\alpha \log p_i, & \quad p_i^\ast = 1 \\ (1 - p_i)^\beta p_i^\alpha \log (1 - p_i), & \quad \textrm{otherwise} \end{cases} \end{equation}\]여기서 $N_r$은 행 구분선의 수이고, $\alpha$와 $\beta$는 각각 2와 4로 설정된 두 개의 hyperparameter이다. $p_i$와 $p_i^\ast$는 \(E'_\textrm{row}\)의 $x_\tau$번째 열에 있는 $i$번째 픽셀에 대한 예측과 ground-truth 레이블이다.
여기에서 $p_i^\ast$는 구분자의 경계에서 잘린 unnormalized Gaussian으로 보강되어 ground-truth 기준점 위치 주변의 페널티를 줄였다. 구체적으로 $(y_k, x_\tau)$는 이 행 구분자의 중심선과 수직선 $x = x_\tau$의 교차점인 $k$번째 행 구분자에 대한 ground-truth 기준점을 나타낸다. $k$번째 행 구분자의 위쪽 경계와 아래쪽 경계 사이의 수직 거리를 두께로 취하고 $w_k$로 표시한다. 그러면 $p_i^\ast$는 다음과 같이 정의할 수 있다.
\[\begin{equation} p_i^\ast = \begin{cases} \exp \bigg( - \frac{(i - y_k)^2}{2 \sigma_k^2} \bigg), & \quad \textrm{if } i \in \bigg( y_k - \frac{w_k}{2}, y_k + \frac{w_k}{2} \bigg) \\ 0, & \quad \textrm{otherwise} \end{cases} \\ \textrm{where} \quad \sigma_k = \sqrt{\frac{w_k^2}{2 \ln (10)}} \end{equation}\]여기서 $\sigma_k$는 구분자의 두께에 따라 달라지며, 이 행 구분자 내의 $p_i^\ast$가 0.1 이상인지 확인한다.
Separation line regression
\[\begin{equation} y = \{(c_i, l_i) \vert i = 1, \cdots, M\} \end{equation}\]을 ground-truth 행 구분자의 집합이라 하자. 여기서 $c_i$는 타겟 클래스이고 $l_i$는 행 구분자의 위치이다.
\[\begin{equation} y^\ast = \{(c_k^\ast, l_k^\ast) \vert k = 1, \cdots, Q\} \end{equation}\]은 예측값의 집합이다. 최적의 이분 매칭 결과 $\hat{\sigma}$를 얻은 후 행 분리선 회귀의 loss는 다음과 같이 계산할 수 있다.
\[\begin{equation} L_\textrm{line}^\textrm{row} = \sum_{i=1}^Q [L_\textrm{cls} (c_i, c_{\hat{\sigma} (i)}^\ast) + \textbf{1}_{\{c_i \ne \emptyset\}} L_\textrm{reg} (l_i, l_{\hat{\sigma} (i)}^\ast)] \end{equation}\]여기서 \(L_\textrm{cls}\)는 focal loss이고 \(L_\textrm{reg}\)는 L1 loss이다.
Auxiliary segmentation loss
행 구분자의 보조 segmentation loss는 binary cross-entropy loss이다.
\[\begin{equation} L_\textrm{aux}^\textrm{row} = \frac{1}{\vert S_\textrm{row} \vert} \sum_{(x, y) \in S_\textrm{row}} \textrm{BCE} (M_\textrm{row} (x, y), M_\textrm{row}^\ast (x, y)) \end{equation}\]여기서 \(S_\textrm{row}\)는 \(M_\textrm{row}\)에서 샘플링된 픽셀 집합이며, \(M_\textrm{row} (x, y)\)와 \(M_\textrm{row}^\ast (x, y)\)는 픽셀 $(x, y)$의 예측된 레이블과 ground-truth 레이블이다. \(M_\textrm{row}^\ast (x, y)\)는 이 픽셀이 행 구분자 내에 있는 경우에만 1이고 그렇지 않으면 0이다.
Cell merging
셀 병합 모듈의 loss는 binary cross-entropy loss이다.
\[\begin{equation} L_\textrm{merge} = \frac{1}{\vert S_\textrm{rel} \vert} \sum_{i \in S_\textrm{rel}} \textrm{BCE} (P_i, P_i^\ast) \end{equation}\]여기서 \(S_\textrm{rel}\)은 샘플링된 셀 쌍 집합을 나타내고, $P_i$와 $P_i^\ast$는 각각 $i$번째 셀 쌍에 대한 예측 레이블과 ground-truth 레이블을 나타낸다.
Overall loss
TSRFormer의 모든 모듈은 함께 학습할 수 있다. 전체 loss function은 다음과 같다.
\[\begin{equation} L = \lambda (L_\textrm{ref}^\textrm{row} + L_\textrm{ref}^\textrm{col}) + L_\textrm{aux}^\textrm{row} + L_\textrm{aux}^\textrm{col} + L_\textrm{line}^\textrm{row} + L_\textrm{line}^\textrm{col} + L_\textrm{merge} \end{equation}\]여기서 $\lambda$는 0.2로 설정된 제어 파라미터이다.
Experiments
- 데이터셋: SciTSR, PubTabNet, WTW, 내부 데이터셋 (In-house)
- 구현 디테일
- backbone: ResNet18-FPN (ImageNet classification task에서 사전 학습된 가중치로 초기화)
- $P_2$의 채널 수: 64
- optimizer = AdamW, batch size = 16
- learning rate: 초기에 $10^{-4}$, polynomial decay schedule
- betas = $(0.9, 0.999)$, weight decay = $5 \times 10^{-4}$
- \(E'_\textrm{row} / E'_\textrm{col}\) = 256
- 쿼리 차원 = 256, 헤드 수 = 16, 피드포워드 네트워크 차원 = 1024
1. Comparisons with Prior Arts
다음은 SciTSR에서의 결과이다. $\ast$는 빈 셀이 없는 경우의 결과이다.

다음은 PubTabNet에서의 결과이다.

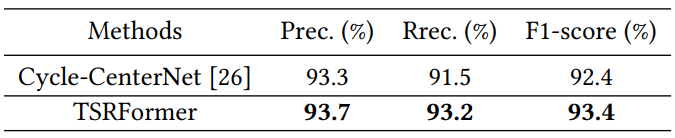
다음은 WTW에서의 결과이다.
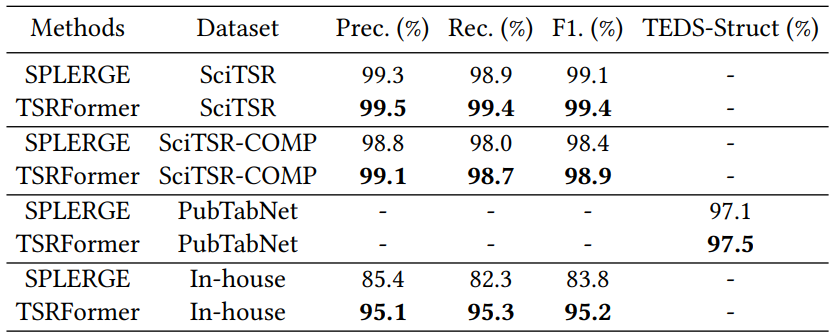
다음은 향상된 SPLERGE와 TSRFormer를 다양한 데이터셋에서 비교한 표이다.
다음은 TSRFormer의 정성적 결과이다. (a-b)는 SciTSR, (c-d)는 PubTabNet, (e-h)는 WTW, (i-l)은 내부 데이터셋에 대한 결과이다.

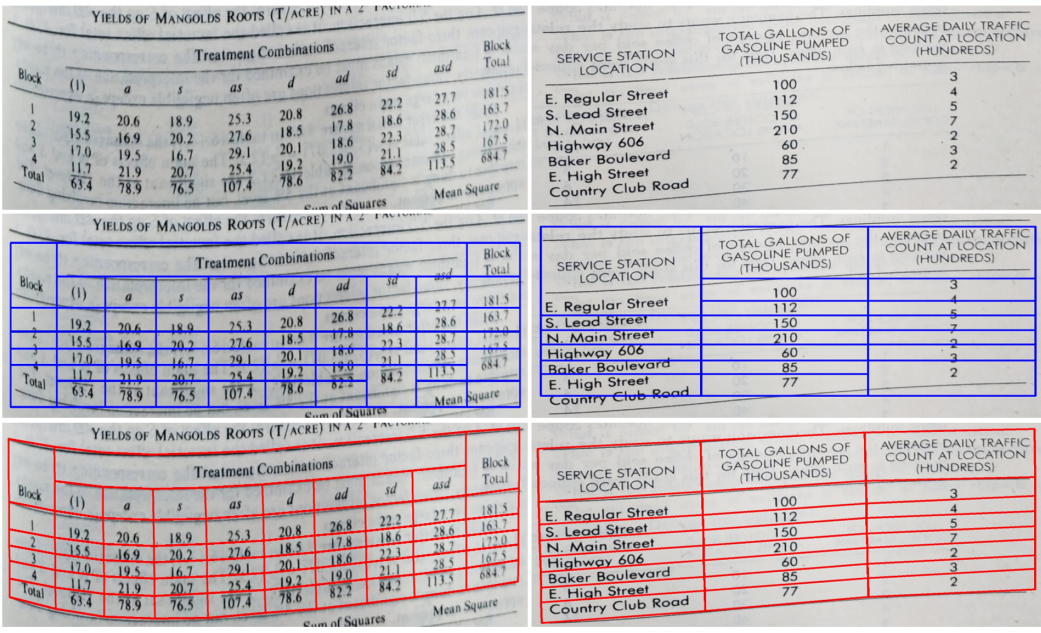
다음은 비뚤어진 표에 대하여 SPLERGE (파란색)와 TSRFormer (빨간색)의 정성적 결과이다.
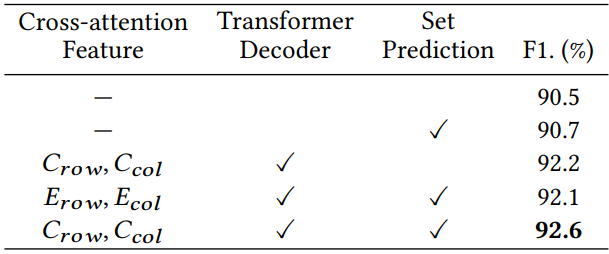
2. Ablation Studies
다음은 TSRFormer의 다양한 모듈에 대한 ablation study 결과이다.

다음은 테두리가 없고 빈칸이 큰 휘어진 표에 대하여 segmentation 기반 접근 방식인 SCNN (가운데)와 TSRFormer (오른쪽)을 정성적으로 비교한 결과이다.

다음은 SepRETR의 디자인에 대한 ablation study 결과이다.
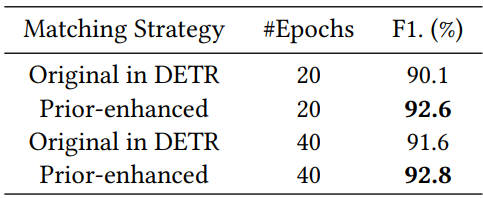
다음은 prior-enhanced 이분 매칭 전략에 대한 ablation study 결과이다.