[논문리뷰] TRIP: Temporal Residual Learning with Image Noise Prior for Image-to-Video Diffusion Models
CVPR 2024. [Paper] [Page]
Zhongwei Zhang, Fuchen Long, Yingwei Pan, Zhaofan Qiu, Ting Yao, Yang Cao, Tao Mei
University of Science and Technology of China | HiDream.ai Inc.
25 Mar 2024
Introduction
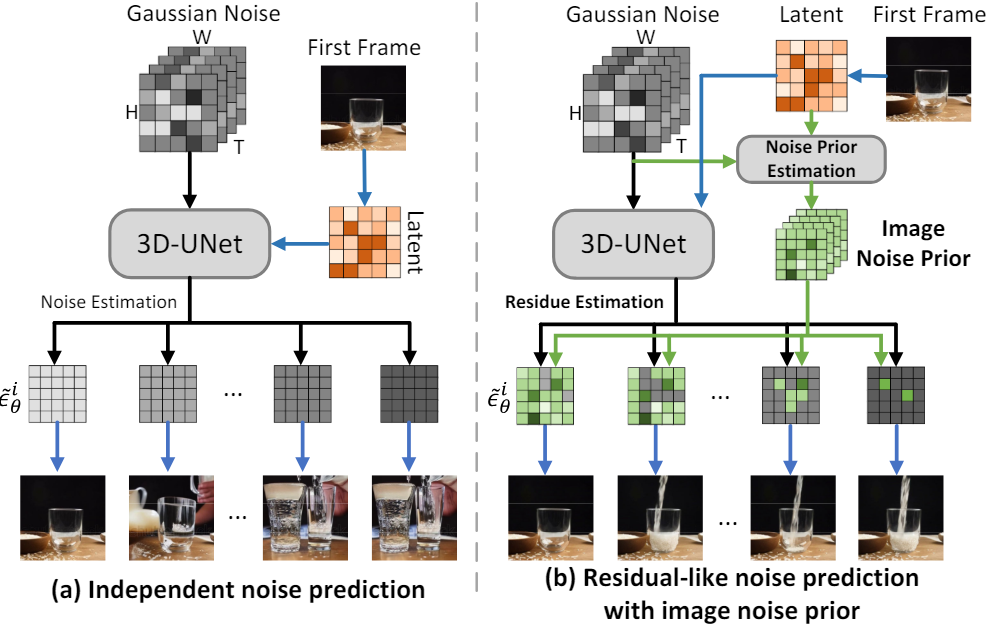
Image-to-Video (I2V)에 대한 최근의 몇 가지 선구적인 관행은 diffusion process 동안 주어진 정적 이미지를 추가 조건으로 직접 활용하여 Text-to-Video (T2V) 생성이 목적인 LDM을 재형성하는 것이다. 위 그림의 (a)는 LDM에서 이러한 기존 noise 예측 전략을 보여준다. 주어진 정적 이미지를 첫 번째 프레임으로 취함으로써 첫 번째 프레임을 이미지 latent code로 인코딩하기 위해 VAE가 먼저 사용된다. 이 인코딩된 이미지 latent code는 학습 가능한 3D-UNet을 통해 각 후속 프레임의 backward diffusion noise를 예측하기 위해 noisy한 동영상 latent code (즉, Gaussian noise 시퀀스)와 추가로 concatenate된다. 각 프레임의 이러한 독립적인 noise 예측 전략은 주어진 이미지와 각 후속 프레임 사이의 고유한 관계를 제대로 활용하지 못하게 하고 인접한 프레임 간의 시간적 일관성을 모델링하는 효율성이 부족하다.
이 문제를 완화하기 위해 본 논문에서는 주어진 이미지의 증폭된 guidance, 즉 image noise prior를 기반으로 temporal residual learning으로 I2V diffusion model의 noise 예측을 공식화하는 새로운 방법을 제시하였다. 위 그림의 (b)에서 볼 수 있듯이 image noise prior만을 참조하여 각 프레임의 backward diffusion noise를 직접 추정하는 추가 shortcut과 일반적인 noise 예측을 통합한다. Image noise prior는 입력 이미지와 noisy한 동영상 latent code를 기반으로 계산되며, 주어진 첫 번째 프레임과 각 후속 프레임 간의 고유 상관관계를 명시적으로 모델링한다. 한편, 이러한 residual 방식은 3D-UNet을 통한 일반적인 noise 예측을 residual noise 예측으로 재구성하여 인접한 프레임 사이의 시간적 모델링을 용이하게 함으로써 시간적으로 보다 일관성 있는 결과를 얻는다.
Residual 방식으로 이미지 조건부 noise 예측을 실행하는 아이디어를 구체화함으로써 I2V 생성을 위한 Temporal Residual learning with Image noise Prior (TRIP)이라는 새로운 diffusion model을 제시하였다. 입력된 noisy한 동영상 latent code와 해당 정적 이미지 latent code가 주어지면 TRIP은 두 가지 경로를 따라 residual noise를 예측한다.
- One-step backward diffusion process를 통해 정적 이미지와 noisy한 동영상 latent code를 기반으로 각 프레임의 레퍼런스 noise, 즉 image noise prior를 얻는 shortcut 경로
- 시간 차원을 따라 정적 이미지와 noisy한 동영상 latent code를 concatenate하고 이를 3D-UNet에 공급하여 각 프레임의 residual noise를 학습하는 residual 경로
최종적으로 Transformer 기반의 시간적 noise 융합 모듈을 활용하여 각 프레임의 레퍼런스 noise와 residual noise를 동적으로 융합하여 주어진 이미지와 충실하게 일치하는 고화질 동영상을 생성한다.
Method
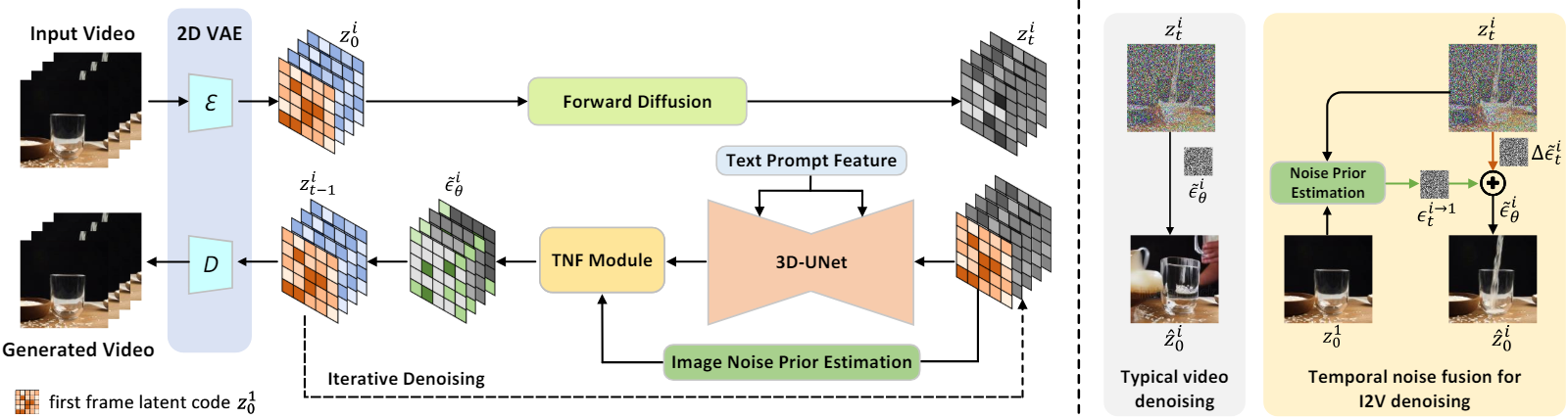
1. Image Noise Prior
일반적인 T2V diffusion model과 달리 I2V 생성 모델은 주어진 첫 번째 프레임과 후속 프레임 간의 충실한 정렬을 추가로 강조한다. 대부분의 기존 I2V 방법들은 첫 번째 프레임의 이미지 latent code를 채널/시간 차원을 따라 noisy한 동영상 latent code와 concatenate하여 동영상 합성을 제어한다. 이러한 방식으로 첫 번째 프레임의 시각적 정보는 시간 모듈을 통해 모든 프레임에 전파된다.
이러한 방법은 동영상 합성을 보정하기 위해 시간 모듈에만 의존하고 주어진 이미지와 각 후속 프레임 사이의 고유한 관계를 제대로 활용되지 않으므로 시간적 일관성 모델링의 효율성이 부족하다. 이 문제를 완화하기 위해 본 논문은 합성된 프레임과 첫 번째 정적 이미지 사이의 정렬을 증폭시키는 것을 목표로 image noise prior를 참조하여 temporal residual learning으로 I2V 생성의 일반적인 noise를 예측한다.
첫 번째 프레임의 이미지 latent code $z_0^1$이 주어지면 이를 시간 차원을 따라 noisy한 동영상 latent code 시퀀스 \(\{z_t^i\}_{i=1}^N\)와 concatenate하여 3D-UNet의 조건부 입력 \(\{z_0^1, z_t^1, z_t^2, \ldots, z_t^N\}\)으로 활용한다. 한편, 첫 번째 프레임의 latent code $z_0^1$과 $i$번째 프레임의 noisy한 latent code $z_t^i$ 간의 상관 관계를 반영하기 위해 image noise prior를 발굴한다. $i$번째 프레임의 latent code $z_0^i$를 backward diffusion process로 다음과 같이 재구성할 수 있다.
\[\begin{equation} z_0^i = \frac{z_t^i - \sqrt{1 - \bar{\alpha}_t} \epsilon_t^i}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \end{equation}\]여기서 \(\epsilon_t^i\)는 $z_0^i$에 추가되는 Gaussian noise이다. 짧은 동영상 클립의 모든 프레임이 본질적으로 첫 번째 프레임과 상관되어 있다는 I2V의 기본 가정을 고려하면, $z_0^i$은 $z_0^1$과 residual 항 $\Delta z^i$의 조합으로 나타낼 수 있다.
\[\begin{equation} z_0^i = z_0^1 + \Delta z^i \end{equation}\]다음으로, 다음과 같이 residual 항 $\Delta z^i$에 scale ratio를 추가하여 변수 $C_t^i$를 구성한다.
\[\begin{equation} C_t^i = \frac{\sqrt{\vphantom{1} \bar{\alpha}_t} \Delta z^i}{\sqrt{1 - \bar{\alpha}_t}} \end{equation}\]식을 정리하면 \(\Delta z^i\)는 다음과 같다.
\[\begin{equation} \Delta z^i = \frac{\sqrt{1 - \bar{\alpha}_t} C_t^i}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \end{equation}\]따라서 첫 번째 프레임의 latent code $z_0^1$은 다음과 같다.
\[\begin{aligned} z_0^1 &= z_0^i - \Delta z^i = \frac{z_t^i - \sqrt{1 - \bar{\alpha}_t} \epsilon_t^i}{\sqrt{\vphantom{1} \bar{\alpha}_t}} - \frac{\sqrt{1 - \bar{\alpha}_t} C_t^i}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \\ &= \frac{z_t^i - \sqrt{1 - \bar{\alpha}_t} (\epsilon_t^i + C_t^i)}{\sqrt{\vphantom{1} \bar{\alpha}_t}} = \frac{z_t^i - \sqrt{1 - \bar{\alpha}_t} \epsilon_t^{i \rightarrow 1}}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \end{aligned}\]여기서 \(\epsilon_t^{i \rightarrow 1}\)는 $z_0^i$과 $z_t^i$ 사이의 관계로 해석될 수 있는 image noise prior로 정의된다. 따라서 image noise prior \(\epsilon_t^{i \rightarrow 1}\)는 다음과 같다.
\[\begin{equation} \epsilon_t^{i \rightarrow 1} = \frac{z_t^i - \sqrt{\vphantom{1} \bar{\alpha}_t} z_0^1}{\sqrt{1 - \bar{\alpha}_t}} \end{equation}\]첫 번째 프레임의 latent code $z_0^1$은 \(\epsilon_t^{i \rightarrow 1}\)와 $z_t^i$를 사용하여 one-step backward diffusion을 통해 직접적으로 재구성될 수 있다. 이와 같이 $z_0^i$가 $z_0^1$에 가까울 때, 즉 $i$번째 프레임이 주어진 첫 번째 프레임과 유사할 때 image noise prior는 $i$번째 프레임의 latent code에 추가되는 Gaussian noise $\epsilon_t^i$에 대한 레퍼런스 noise로 작용한다.
2. Temporal Residual Learning
Shortcut 경로에서 학습된 image noise prior는 시간적 모델링을 용이하게 하여 첫 번째 프레임과 후속 프레임 간의 정렬을 증폭한다. 인접한 모든 프레임 간의 시간적 일관성을 더욱 강화하기 위해 프레임 간 관계적 추론을 통해 각 프레임의 residual noise를 추정하는 residual 경로를 추가한다. 저자들은 동영상 편집을 위해 사전 학습된 3D-UNet의 prior를 사용하는 Gen-L-Video에서 영감을 받아 3D-UNet을 fine-tuning하여 각 프레임의 residual noise를 추정할 것을 제안하였다.
$i$번째 프레임의 추정 noise \(\tilde{\epsilon}_t^i\)는 image noise prior \(\epsilon_t^{i \rightarrow 1}\)와 추정된 residual noise \(\Delta \tilde{\epsilon}_t^i\)의 조합이다.
\[\begin{equation} \tilde{\epsilon}_t^i = \lambda^i \epsilon_t^{i \rightarrow 1} + (1 - \lambda^i) \Delta \tilde{\epsilon}_t^i \end{equation}\]여기서 $\lambda^i$는 trade-off 파라미터이며, \(\Delta \tilde{\epsilon}_t^i\)는 3D-UNet에 의해 학습된다. I2V diffusion 목적 함수 \(\tilde{\mathcal{L}}\)은 다음과 같이 계산된다.
\[\begin{equation} \tilde{\mathcal{L}} = \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I), t, c, i} [\| \epsilon_t^i - \tilde{\epsilon}_t^i \|^2] \end{equation}\]\(\tilde{\epsilon}_t^i\)의 계산은 각 프레임의 backward diffusion noise를 추정하는 Temporal Noise Fusion 모듈을 통해 작동된다. 또한 인덱스 $i$를 증가함에 따라 $i$번째 프레임과 첫 번째 프레임 사이의 시간적 상관관계가 감소하기 때문에 $i$에 대해 선형 감쇠 파라미터로 $\lambda^i$를 형성한다.
3. Temporal Noise Fusion Module
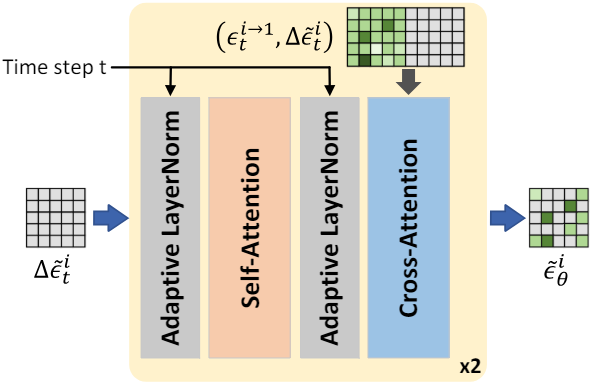
Residual 방식의 이중 경로 noise 예측은 인접한 프레임 간의 시간적 모델링을 용이하게 하기 위해 레퍼런스로 image noise prior를 탐색한다. 그러나 간단한 선형 융합을 사용하는 TNF 모듈의 수작업 설계에는 hyperparameter $\lambda^i$의 세심한 튜닝이 필요하므로 최적이 아닌 생성 결과를 보인다. 대신, image noise prior와 residual noise를 동적으로 융합하는 새로운 Transformer 기반 Temporal Noise Fusion (TNF) 모듈을 고안하여 noise 융합 사이의 관계를 더욱 활용하고 향상시키는 것을 목표로 한다.
위 그림은 TNF 모듈의 구조이다. 추정된 residual noise \(\Delta \tilde{\epsilon}_t^i\)가 주어지면 먼저 공간적 feature 정규화를 위해 timestep $t$에 의해 변조되는 adaptive layer norm 연산을 활용한다. 그 후, feature 향상을 위해 하나의 self-attention layer가 사용되고 동일한 adaptive layer norm 연산이 이어진다. 다음으로, 프로세스 내 중간 feature를 query로 사용하고 concatenate된 feature \([\epsilon_t^{i \rightarrow 1}, \Delta \tilde{\epsilon}_t^i]\)를 key/value로 사용하여 cross-attention layer를 통해 최종 backward diffusion noise \(\tilde{\epsilon}_\theta (z_t, t, c, i)\)를 얻는다.
\[\begin{equation} \tilde{\epsilon}_\theta (z_t, t, c, i) = \tilde{\epsilon}_t^i = \varphi (\Delta \tilde{\epsilon}_t^i, \epsilon^{i \rightarrow 1}, t) \end{equation}\]여기서 $\varphi$는 TNF 모듈이다. Transformer 기반 TNF 모듈은 hyperparameter 튜닝을 회피하고 각 프레임의 image noise prior와 residual noise를 동적으로 병합하여 충실도가 높은 동영상을 생성한다.
Experiments
- 데이터셋: WebVid-10M, DTDB, MSR-VTT
- 구현 디테일
- 3D-UNet: Stable-Diffusion v2.1에서 가져옴
- 학습 샘플: 각 16 프레임, 샘플링레이트는 4 fps
- 해상도: 256$\times$256
- noise scheduler: linear ($\beta_1 = 1 \times 10^{-4}$, $\beta_T = 2 \times 10^{-2}$)
- timestep 수: $T = 1000$
- 샘플링 전략: DDIM (50 steps)
- optimizer: AdamW
- learning rate: 3D-UNet은 $2 \times 10^{-6}$, TNF 모듈은 $2 \times 10^{-4}$
- GPU: NVIDIA A800 8개
1. Comparisons with SOTA Methods
WebVid-10M


DTDB
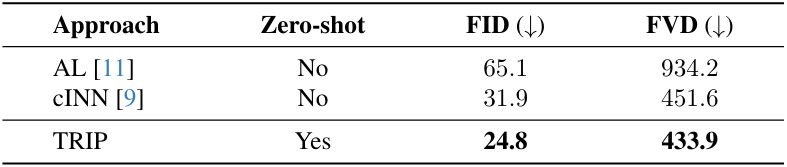

MSR-VTT
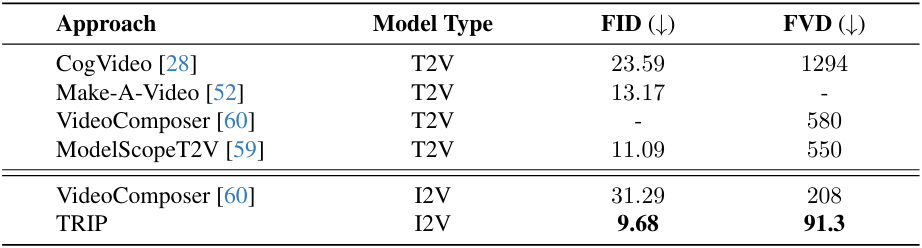
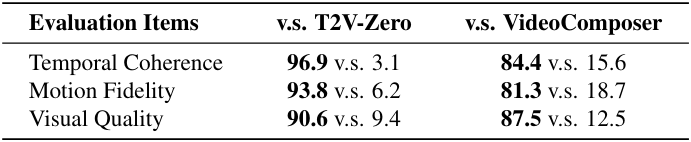
2. Human Evaluation
다음은 WebVid-10M에서의 인간 평가 결과이다.
3. Ablation Study
다음은 여러 컨디셔닝 방법에 대한 성능을 비교한 표이다. (WebVid-10M)
- $\textrm{TRIP}_C$: 채널 차원을 따라 $z_0^1$과 $z_t^i$를 concatenate
- TRIPTE: 시간 차원을 따라 $z_t^i$의 끝 부분에 $z_0^1$를 concatenate
- TRIP: 시간 차원을 따라 $z_t^i$의 시작 부분에 $z_0^1$를 concatenate (논문에서 제안한 방법)
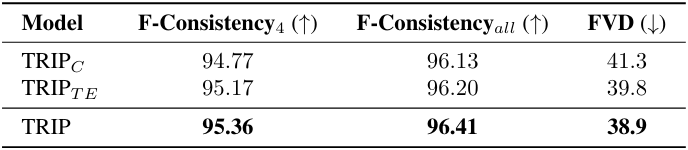
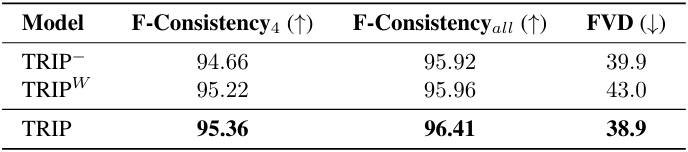
다음은 temporal residual learning에 대한 ablation 결과이다. (WebVid-10M)
- TRIP-: temporal residual learning의 shortcut을 제거하고 noise 예측을 위해 3D-UNet만 활용
- TRIPW: 선형 융합 전략을 통해 image noise prior와 residual noise를 단순히 융합

4. Application: Customized Image Animation
다음은 Stable-Diffusion XL을 사용하여 이미지 애니메이션을 커스터마이징한 결과이다.

다음은 이미지 편집 모델 (ex. InstructPix2Pix, ControlNet)로 이미지 애니메이션을 커스터마이징한 결과이다.
