[논문리뷰] Triangle Splatting for Real-Time Radiance Field Rendering

3DV 2026. [Paper] [Page] [Github]
Jan Held, Renaud Vandeghen, Adrien Deliege, Abdullah Hamdi, Silvio Giancola, Anthony Cioppa, Andrea Vedaldi, Bernard Ghanem, Andrea Tagliasacchi, Marc Van Droogenbroeck
University of Liege | KAUST | University of Oxford | Simon Fraser University | University of Toronto | Google DeepMind
25 May 2025

Introduction

본 논문에서는 Triangle Splatting이라는 실시간 미분 가능한 렌더러를 소개한다. 이 렌더러는 삼각형들을 화면 공간에 splatting하여 표현하는 동시에 end-to-end 기반 최적화를 가능하게 한다. Triangle Splatting은 Gaussian의 적응성과 삼각형 primitive의 효율성을 결합하여, 3DGS, 2DGS, 3DCS 보다 시각적 완성도, 학습 속도, 렌더링 처리량 면에서 우수한 성능을 보여준다. 최적화된 triangle soup은 모든 메쉬 기반 렌더러와 직접 호환된다. 본 논문에서 제안하는 표현 방식은 기존 게임 엔진에서 1280$\times$720 해상도에서 2,400 FPS 이상의 속도로 렌더링될 수 있어 높은 효율성과 원활한 호환성을 입증하였다. Triangle Splatting은 novel view synthesis와 3D 재구성을 위해 삼각형 primitive를 직접 최적화하는 최초의 splatting 기반 접근 방식으로, 기존 렌더링 파이프라인과 최신 미분 가능한 프레임워크를 연결하면서 SOTA 결과를 제공한다.

Method

1. Differentiable rasterization

사용하는 primitive는 3D 삼각형 \(T_\textrm{3D}\)이며, 각 삼각형은 세 개의 vertex \(\textbf{v}_i \in \mathbb{R}^3\), 색상 \(c\), smoothness 파라미터 $\sigma$, 그리고 불투명도 $o$로 정의된다. 세 vertex는 최적화 과정에서 자유롭게 움직일 수 있다. 삼각형을 렌더링하기 위해 먼저 핀홀 카메라 모델을 사용하여 각 vertex \(\textbf{v}_i\)를 이미지 평면에 projection한다.

\[\begin{equation} \textbf{q}_i = \textbf{K} (\textbf{R} \textbf{v}_i + \textbf{t}) \in \mathbb{R}^2 \end{equation}\]

($\textbf{K}$는 intrinsic, $[\textbf{R} \vert \textbf{t}]$는 extrinsic)

\(\textbf{q}_i\)는 2D 이미지 공간에서 projection된 삼각형 \(T_\textrm{2D}\)를 형성한다. 삼각형을 완전히 불투명하게 렌더링하는 대신, 픽셀 $\textbf{p}$를 $[0, 1]$ 내의 값으로 매핑하는 window function $I$를 기반으로 삼각형의 영향을 부드럽게 가중치 부여한다. 삼각형이 projection되면, 각 이미지 픽셀 $\textbf{p}$의 색상은 깊이 순서대로 겹치는 모든 삼각형의 기여도를 누적하여 계산하며, 이때 $I(\textbf{p})$ 값을 불투명도로 간주한다. 렌더링 방정식은 3DGS에서 사용된 것과 동일하다.

Window function

먼저 이미지 공간에서 2차원 삼각형의 SDF $\phi$를 정의한다.

\[\begin{equation} \phi (\textbf{p}) = \max_{i \in \{1, 2, 3\}} (\textbf{n}_i \cdot \textbf{p} + d_i) \end{equation}\]

(\(\textbf{n}_i\)는 삼각형 바깥쪽을 향하는 삼각형 edge의 unit normal 벡터, $d_i$는 삼각형이 함수 $\phi$의 zero-level set으로 주어지도록 하는 offset)

따라서 SDF $\phi$는 삼각형 바깥쪽에서 양수 값을, 안쪽에서 음수 값을 가지며 경계에서는 0이다. Window function $I$는 다음과 같이 정의된다.

\[\begin{equation} I(\textbf{p}) = \left( \textrm{ReLU}\left( \frac{\phi (\textbf{p})}{\phi (\textbf{s})} \right) \right)^\sigma \end{equation}\]

($\textbf{s} \in \mathbb{R}^2$는 projection된 삼각형의 내심)

$I$는 삼각형 내심에서 1, 경계에서 0, 삼각형 외부에서 0이 된다. $\sigma > 0$는 삼각형의 내심과 경계 사이의 전환을 제어하는 smoothness 파라미터이다. 이 공식은 세 가지 중요한 성질을 가지고 있다.

1. 삼각형 내부에 window function이 최댓값 1을 갖는 점(내심)이 존재한다.
2. Window function은 경계와 삼각형 외부에서 0이 되어 윈도우 함수의 지지 영역이 삼각형에 밀착된다.
3. 하나의 파라미터로 window function의 smoothness를 쉽게 제어할 수 있다.

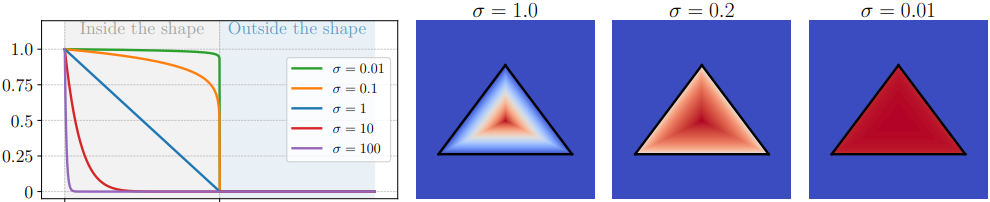
위 그림은 $\sigma$의 다양한 값에 대해 이 세 가지 속성이 모두 만족됨을 보여준다. $\sigma \rightarrow 0$일 때 채워진 삼각형으로 수렴하는 반면, $\sigma$ 값이 클수록 경계에서 0에서 중심으로 갈수록 1로 점진적으로 증가하는 부드러운 window function이 생성된다.

2. Adaptive pruning and splitting

삼각형은 공간 영역이 밀집되어 있고, 따라서 gradient도 밀집되어 있다. 따라서 삼각형의 밀도와 표현력을 조절하여 공간 영역을 삼각형이 덮는 범위를 제어하는 ​​메커니즘이 필요하다. 이는 3DGS와 유사하게 pruning과 densification 루틴을 통해 구현된다.

Pruning

Rasterization 과정에서 각 삼각형에 대해 최대 볼륨 렌더링 블렌딩 가중치 $T \cdot o$를 계산하고, 모든 학습 뷰에서 최대 가중치가 threshold \(\tau_\textrm{prune}\)보다 작은 모든 삼각형을 제거한다. 또한, 한 픽셀을 초과하는 면적으로 최소 두 번 이상 렌더링되지 않은 모든 삼각형은 제거한다. 즉, 학습 데이터에 overfitting되었을 가능성이 높은 삼각형을 제거한다. 아래 그림은 pruning 전략의 효과를 보여준다.

Densification

저자들은 삼각형 추가를 위해 휴리스틱에 의존하는 대신, 3DGS-MCMC에서 제시한 MCMC 기반의 확률적 프레임워크를 채택하였다. 각 densification 단계에서 확률 분포에서 샘플링하여 새로운 삼각형을 추가할 위치를 결정한다. 불투명도 $o$와 smoothness $\sigma$는 모두 학습 과정에서 얻어지므로, 베르누이 샘플링에 $1/\sigma$와 $o$를 번갈아 사용함으로써 확률 분포를 직접 구축한다. 특히, $\sigma$ 값이 낮은 삼각형, 즉 속이 채워진 삼각형을 우선적으로 샘플링한다. Window function 덕분에 삼각형의 영향은 projection된 geomtery에 의해 제한되며 삼각형 내부에 국한된다.

고밀도 영역에서는 각 픽셀에서 많은 삼각형이 겹쳐지므로 각 도형이 더 높은 $\sigma$ 값을 가지게 되어 더 부드러운 결과물을 얻을 수 있다. 반대로 저밀도 영역에서는 픽셀에 영향을 미치는 삼각형의 수가 적기 때문에 각 삼각형이 재구성 과정에 더 많은 기여를 해야 한다. 결과적으로 각 삼각형은 내부 영역에 걸쳐 기여도를 높이기 위해 더 낮은 $\sigma$ 값을 가지게 되며, 이를 통해 기하학적 경계 내에서 최대한의 영역을 커버하여 더욱 선명한 결과물을 만들어낸다.

또한, 저자들은 3DGS-MCMC에서 영감을 받아 샘플링 과정을 방해하지 않도록 업데이트를 설계했다. 특히, 상태의 확률(즉, 모든 삼각형의 현재 파라미터 집합)이 업데이트 전후에 변하지 않도록 하여, 동일한 확률을 가진 샘플 간의 이동으로 해석될 수 있도록 하고 Markov chain의 무결성을 유지하였다. 샘플링 단계 전반에 걸쳐 일관된 표현을 유지하기 위해 선택된 삼각형에 중점 분할(midpoint subdivision)을 적용한다. 각 삼각형은 edge의 중점을 연결하여 네 개의 작은 삼각형으로 분할되며, 이를 통해 새 삼각형들의 면적과 공간 영역이 원래 삼각형과 일치하도록 한다. 삼각형은 3D vertex로 정의되므로 이 연산은 간단하게 수행할 수 있다. 마지막으로, 삼각형의 크기가 임계값 $\tau_\textrm{small}$보다 작으면 분할하지 않고 복제한 후 삼각형 평면 방향을 따라 랜덤 노이즈를 추가한다.

3. Optimization

최적화는 SfM을 통해 얻은 카메라 파라미터, 카메라 포즈, sparse한 포인트 클라우드에서 시작한다. 이 포인트 클라우드의 각 3D 포인트에 대해 3D 삼각형을 생성한다. 그리고 주어진 뷰에서 발생하는 렌더링 오차를 최소화하여 모든 3D 삼각형의 3D vertex 위치 \(\{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3\}\), smoothness $\sigma$, 불투명도 $o$, spherical harmonics 색상 계수 $\textbf{c}$를 최적화한다.

3D 삼각형은 대략 정삼각형이고, orientation이 랜덤하며, 크기는 가장 가까운 세 이웃 포인트까지의 평균 거리 $d$에 비례한다. 이를 위해 단위 구에서 세 개의 vertex \(\{\textbf{u}_1, \textbf{u}_2, \textbf{u}_3\}\)을 균일하게 랜덤 샘플링하고, 모두 $d$만큼 확대한 다음, SfM 포인트 $\textbf{q} \in \mathbb{R}^3$을 더하여 $\textbf{q}$를 중심으로 배치한다.

\[\begin{equation} \textbf{v}_i = \textbf{q} + k \cdot d \cdot \textbf{u}_i \end{equation}\]

($k \in \mathbb{R}$는 scaling 상수)

학습 loss는 photometric loss (\(\mathcal{L}_1\), \(\mathcal{L}_\textrm{D-SSIM}\)), 3DGS-MCMC의 opacity loss \(\mathcal{L}_o\), 2DGS의 distortion loss \(\mathcal{L}_d\) 및 normal loss \(\mathcal{L}_n\)의 결합이다. 또한, 더 큰 삼각형을 유도하기 위해 크기 정규화 항

\[\begin{equation} \mathcal{L}_s = 2 \| (\textbf{v}_1 - \textbf{v}_0) \times (\textbf{v}_2 - \textbf{v}_0) \|_2^{-1} \end{equation}\]

를 추가한다. 최종 loss \(\mathcal{L}\)은 다음과 같다.

\[\begin{equation} \mathcal{L} = (1 - \lambda) \mathcal{L}_1 + \lambda \mathcal{L}_\textrm{D-SSIM} + \beta_1 \mathcal{L}_o + \beta_2 \mathcal{L}_d + \beta_3 \mathcal{L}_n + \beta_4 \mathcal{L}_s \end{equation}\]

Experiments

1. Novel-view synthesis

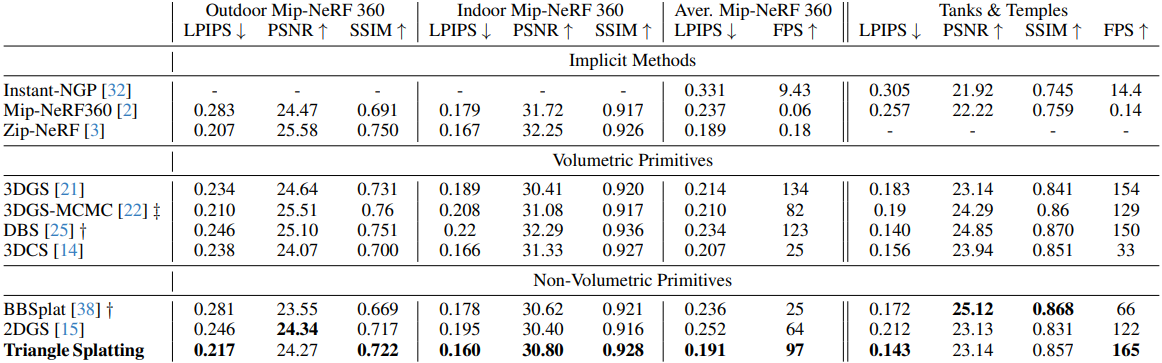
다음은 렌더링 품질을 비교한 결과이다.

2. Speed & Memory

다음은 학습 속도 및 메모리를 비교한 표이다.

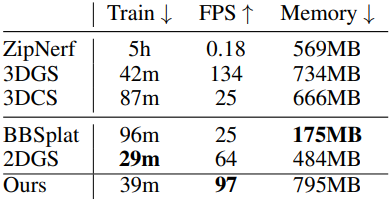
다음은 하드웨어와 해상도에 따른 FPS를 비교한 표이다.

3. Ablations

다음은 ablation study 결과이다.

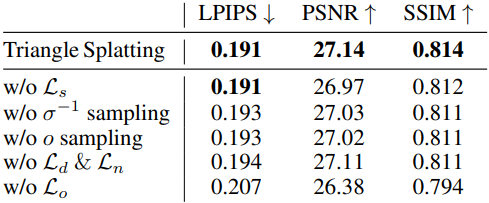
다음은 window function에 대한 ablation 결과이다. 왼쪽은 sigmoid function을 window function으로 사용하였을 때의 결과이다.