[논문리뷰] Transformer²: Self-adaptive LLMs

ICLR 2025. [Paper] [Blog] [Github]
Qi Sun, Edoardo Cetin, Yujin Tang
Sakana AI | Institute of Science Tokyo
9 Jan 2025

Introduction

Self-adaptive LLM은 AI에서 상당한 진전을 나타내며, 모델이 다양한 task와 동적 컨텍스트에 실시간으로 적응할 수 있는 프레임워크를 제공한다. 효과적인 적응에는 compositionality(조합 가능성)와 scalability(확장 가능성)가 필수적이지만, 현재의 LLM 학습 방법론은 이 두 가지 속성을 동시에 달성하지 못한다. 본 논문은 이 비전을 실현하고 이러한 격차를 해소하기 위한 솔루션을 제시하는 것을 목표로 하였다.

전통적으로 LLM post-training은 하나의 광범위한 학습 세션에서 광범위한 역량에 대한 모델을 최적화하려고 했다. 이 one-shot fine-tuning 프레임워크는 단순성 관점에서 이상적이지만 실제로 만들기 어렵다. 예를 들어 post-training은 여전히 ​​리소스 집약적이어서 상당한 계산 비용과 학습 시간이 발생한다. 또한 데이터를 추가로 도입할 때 눈에 띄는 성능 상충이 발생하는 경향이 있어 overfitting과 task 간섭을 동시에 극복하기 어렵다.

대조적으로, self-adaptive 모델은 보다 유연하고 효율적인 접근 방식을 제공한다. 한 번에 모든 task에 대한 LLM을 학습시키려고 시도하는 대신, expert 모듈을 따로 개발하여 필요에 따라 기본 LLM에 증강할 수 있다. 이를 통해 모델은 지속적으로 재조정할 필요 없이 task에 따라 동적으로 동작을 수정할 수 있다. 독립적인 구성 요소를 갖는 이점 외에도 이 모듈성은 지속적인 학습을 지원하여 모델이 시간이 지남에 따라 catastrophic forgetting 없이 새로운 기술을 추가할 수 있도록 한다.

원칙적으로, self-adaptive LLM을 만들기 위해서는 먼저 expert 모듈들을 각각 LoRA와 같은 기술을 통해 fine-tuning하여 개발하는 것이다. 그런 다음 이러한 expert 모듈은 task 요구 사항에 따라 런타임에 동적으로 구성될 수 있으며, 이 프로세스는 Mixture of Experts (MoE)와 같은 시스템을 통해 효율적으로 관리할 수 있다. 그러나 이 접근 방식의 scalability와 compositionality를 위해서는 몇 가지 과제를 해결해야 한다.

1. 여러 expert 모듈을 만들기 위해 LLM을 fine-tuning하면 학습해야 하는 파라미터 수가 크게 늘어난다.
2. Expert 모듈은 종종 overfitting되기 쉽다. 특히 작은 데이터셋이나 좁은 task 도메인에서 학습할 때 흔히 나타나는 현상이다.
3. Expert 모듈의 유연하게 조합하는 것은 현재 거의 해결되지 않은 문제이다.

이러한 한계를 극복하기 위해, 저자들은 먼저 self-adaptation을 위한 새로운 parameter-efficient fine-tuning (PEFT) 방법인 Singular Value Fine-tuning (SVF)을 제안하였다. SVF는 모델의 가중치 행렬 내에서 특이값(singular value)만 추출하고 튜닝한다. 이를 통해 overfitting의 위험을 완화하고, 계산량을 요구 사항을 크게 줄이며, 내재적인 compositionality을 허용한다. 이러한 속성을 통해 RL로 좁은 데이터셋에서 학습하여 효과적인 도메인별 expert 벡터들을 저렴하게 얻을 수 있으며, 개별 주제에 대한 task 성능을 직접 최적화한다.

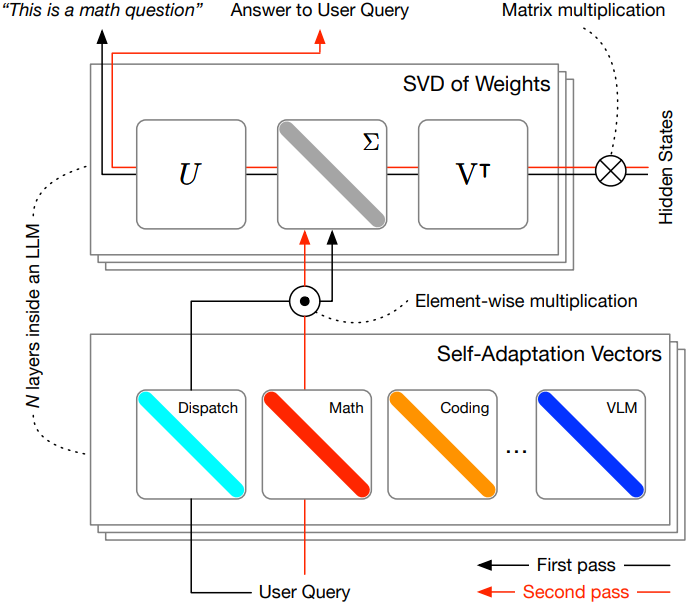
그런 다음 저자들은 LLM이 self-adaptation의 기본 원칙을 통해 힘을 얻을 수 있도록 Transformer² 프레임워크를 소개하였다. 모르는 task에서 프롬프트가 주어지면 Transformer²는 2단계 inference 메커니즘을 사용한다. 첫 번째 단계에서 Transformer²는 모델을 실행하고 test-time 동작을 관찰하여 관련 정보를 수집하여 현재 문제를 해결하는 데 필요한 기술을 이해한다. 두 번째 단계에서는 이 정보를 사용하여 사용 가능한 expert 벡터를 결합하고 test-time 조건에 맞게 특별히 튜닝된 LLM의 기본 가중치에 대한 새로운 수정을 제공한다. 저자들은 Transformer² 내에서 사용할 수 있는 세 가지 다른 적응 전략을 설계하여 test-time 조건에 대한 접근성을 높이면서 성능적인 이점을 제공하였다.

SVF는 도메인별 데이터셋에서 학습했을 때 LoRA와 같은 기존 fine-tuning 전략보다 지속적으로 성능이 뛰어나며, 동시에 파라미터가 수십 배 더 적다. Transformer²는 VQA와 같은 완전히 out-of-distribution인 task에서도 기본 모델의 가중치를 효과적으로 조정하여 성능을 훨씬 더 높다. 또한, 저자들은 현재 test-time 조건에 대한 추가 액세스를 제공하고 모델 아키텍처 전반에 걸쳐 사전 학습된 SVF expert들을 재활용할 수 있도록 하여 이점을 증가시켰다.

Method

1. Singular value fine-tuning

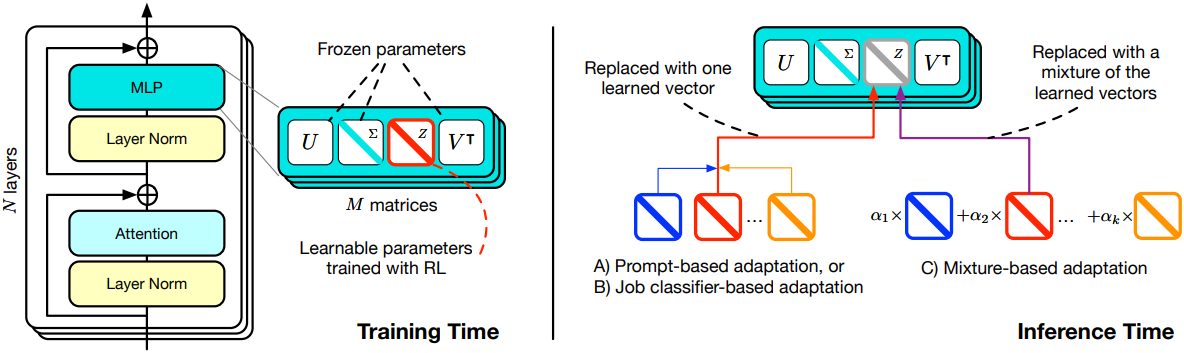
SVF는 Transformer²의 핵심 구성 요소이며, fine-tuning을 위한 매우 효율적인 parameterization을 제공하고 적응을 위한 고유한 compositionality를 제공한다. 기존의 fine-tuning 기술은 종종 가중치 행렬을 수정하여 사전 학습된 모델을 새로운 능력으로 보강하는 것을 목표로 한다. 그러나 LLM의 Transformer 가중치는 사전 학습 데이터의 폭과 광범위한 아키텍처 디자인 덕분에 이미 추상화된 지식의 풍부한 저장소이다. 많은 연구들에서 입증되었듯이 많은 다운스트림 task를 해결하는 데 필요한 능력은 사전 학습된 모델 내에 이미 존재한다.

따라서 효율적인 fine-tuning 방법은 새로운 능력을 추가하려고 하는 대신 이러한 잠재적 능력을 보다 표현 가능하게 만드는 데 중점을 두어야 한다. SVF는 모든 가중치 행렬 $W \in \mathbb{R}^{m \times n}$에 대해 간단한 벡터 $z \in \mathbb{R}^{r}$을 학습하여 새로운 가중치 행렬 $W^\prime$을 생성한다.

\[\begin{equation} W = U \Sigma^\prime V^\top, \quad \textrm{where} \; \Sigma^\prime = \Sigma \otimes \textrm{diag}(z) \end{equation}\]

이 parameterization은 여러 가지 이점을 제공한다.

무시할 수 있는 파라미터

각 가중치 행렬에 대해 벡터 $z$만 학습하면 이전 방식들보다 최적화에 필요한 파라미터가 수십 배 더 적어 매우 효율적인 fine-tuning이 가능하다. 예를 들어, LoRA는 가중치 행렬당 $(m+n) \times r^\prime$개의 학습 가능한 파라미터가 필요하다. 여기서 $r^\prime$은 일반적으로 표현력을 위해 충분히 크게 설정해야 하는 hyperparameter이다. LoRA-XS와 같은 최근 방법은 효율성을 한층 더 끌어올리려고 하지만, 종종 여러 실제 시나리오에서 적용성을 제한하는 제한적인 가정을 도입하였다.

반대로 SVF는 $r = \min (m, n)$개의 파라미터만 필요하지만, LLM의 가중치에 압축된 잠재적 표현력이 제공하는 매우 의미 있는 공간에서 작동하기 때문에 동일한 단점이 나타나지 않는다. SVF가 특이값만 스케일링하는 것은 표현력이 제한되는 것처럼 보일 수 있지만, full-rank 방식으로 가중치 행렬에 영향을 미치기 때문에 기술적으로는 low-rank 방식보다 더 많은 정보를 제공한다.

높은 compositionality

독립적인 $U$, $\Sigma$, $V$로 가중치를 분해하면 학습된 $z$ 벡터가 쉽게 조합 가능하고 해석 가능해져 대수적 조작을 통해 수많은 적응 가능성이 열린다. 반면 LoRA 기반 방법은 본질적으로 이러한 속성이 부족하다. 예를 들어, 동일한 task에서 학습한 두 LoRA가 각 $W$에 대해 정확히 동일하게 학습하더라도 압축된 $A$와 $B$ 행렬 사이를 직접 보간하면 원래 동작을 보존할 가능성이 낮다.

원칙적인 정규화

$U$, $\Sigma$, $V$의 magnitude를 수정하면 원칙적이고 효과적인 정규화 형태가 제공된다. 실제로 이 속성을 사용하면 심각한 collapse나 overfitting의 위험 없이 수백 개의 데이터만으로 임의의 다운스트림 task를 fine-tuning할 수 있다.

2. End-to-end optimization with RL

RL로 임의의 언어 모델 \(\pi_{\theta_W}\)를 fine-tuning하기 위해 SVF 벡터의 집합 \(\theta_z = \{z_1, \cdots, z_{N \times M}\}\)을 학습시켜 task 성능을 위해 직접 최적화한다. 여기서 \(\theta_W = \{W_1, \cdots, W_{N \times M}\}\)은 가중치 행렬의 집합이며, $N$은 레이어의 수이고 $M$은 레이어당 fine-tuning할 가중치 행렬의 수이다.

저자들은 REINFORCE 알고리즘을 사용하였고, 각 프롬프트 $x_i \in D$에 대해 생성된 답변 $y_i$에 정확성에 따른 reward \(r \in \{−1, 1\}\)을 할당하였다. 추가로 원래 모델의 동작에서 벗어나는 데 대한 KL 페널티를 목적 함수에 추가하였다. 따라서 최종 목적 함수는 다음과 같다.

\[\begin{equation} J(\theta_z) = \mathbb{E} [\log (\pi_{\theta_{W^\prime}} (\hat{y}_i \, \vert \, x_i)) \, r (\hat{y}_i, y_i)] - \lambda D_\textrm{KL} (\pi_{\theta_{W^\prime}} \| \pi_{\theta_W}) \end{equation}\]

(\(\pi_{\theta_{W^\prime}}\)는 원래 가중치 행렬 $W$를 $W^\prime$로 대체한 언어 모델)

RL은 일반적으로 next-token prediction보다 덜 안정적이라고 여겨지지만, SVF의 정규화 특성이 이전의 제약이 적은 parameterization의 많은 실패 모드를 피한다. 따라서 이러한 보완적인 구성 요소를 효과적으로 결합하면, 대규모 데이터셋을 사용하는 값비싼 fine-tuning 절차에 의존하지 않고 task 성능을 end-to-end로 직접 극대화할 수 있다.

일반적으로 RL을 사용한 SVF는 학습하는 데이터셋에 대한 요구 사항이 낮다. 예를 들어, LoRA fine-tuning은 next-token prediction을 수행하기 위해 “설명 텍스트”가 필요하므로 데이터셋에 대한 요구 사항이 더 높다. 이러한 이점 덕분에 SVF는 더 일반적이고 효과적일 수 있다.

3. Self-adaptation

저자들은 LLM의 inference 단계에 초점을 맞추었으며, SVF로 학습된 $K$개의 기본 “expert” 벡터 세트 $z^{1:K}$를 결합하여 다양한 종류의 능력을 제공하는 간단한 2단계 적응 전략을 고안하였다.

첫 번째 inference 단계에서 task 또는 개별 입력 프롬프트가 주어지면, Transformer²는 모델을 실행하고 test-time 동작을 관찰하여 test-time 조건에 맞게 튜닝된 새로운 $z^\prime$ 벡터를 도출한다. 이 적응된 $z^\prime$은 두 번째 inference 단계에서 실제 응답을 제공하는 데 사용된다. SVF로 학습된 expert 벡터와 적응 전략 간의 상호 작용은 원활한 통합을 보장하며, 적응 전략은 입력 task를 처리하기 위해 가장 적합한 expert 벡터의 조합을 동적으로 결정하고 조합한다.

저자들은 첫 번째 inference 단계 동안 벡터 $z^\prime$을 생성하는 세 가지 간단한 접근 방식을 제안하여 self-adaptation을 구현하였다.

Prompt engineering

가장 기본적인 접근 방식은 LLM에 입력 프롬프트를 분류하도록 직접 요청하는 데 사용하는 새로운 “adaptation” 프롬프트를 구성하는 것이다. 그런 다음 응답을 기반으로 각 SVF expert들을 학습시키는 데 사용된 도메인 집합에서 하나의 카테고리를 추출한다. 즉, $z^{1:K}$에서 직접 $z^\prime$을 선택한다. Adaptation 프롬프트에서 “Others” 카테고리에 대한 옵션도 명시적으로 제공하여 expert들이 적절한 능력을 제공하지 않는 경우 모델이 기본 가중치를 사용할 수 있도록 한다. 다음은 adaptation 프롬프트를 구성하는 데 사용된 형식이다.

Classification expert

프롬프트 엔지니어링 방식은 task 식별을 처리하기 위해 특수 시스템을 사용하는 것이다. Self-adaptation의 원칙에 따라 SVF를 적용하여 이 task를 처리하도록 기본 LLM 자체를 fine-tuning한다.

먼저, $K$개의 SVF 학습 task에서 데이터셋 \(D = \{(x_{i,k}, k)\}\)를 수집한다. 여기서 $x_{i,k}$는 $k$번째 task의 $i$번째 예제이다. 그러면 각 $(x_{i,k}, k)$는 task classification expert $z^c$를 사전 학습시키기 위한 예제들을 형성한다. 첫 번째 inference 단계 동안에는 $z^c$를 로드하여 기본 모델의 고유한 task 분류 능력을 개선하여 입력 프롬프트를 처리할 더 적절한 $z^\prime$을 선택한다.

Few-shot adaptation

세 번째 방법은 개별 프롬프트를 넘어 test-time 조건에 대한 확장된 액세스를 가정하여 추가 task 정보를 활용하며, few-shot prompting에서 영감을 받았다.

최적화된 각 $W$에 대해 각각 계수 \(\alpha_k\)로 가중된 $K$개의 학습된 SVF 벡터들 사이를 linear interpolation하여 완전히 새로운 $z^\prime$을 생성한다.

\[\begin{equation} z^\prime = \sum_{k=1}^K \alpha_k z_k \end{equation}\]

Cross-entropy method(CEM)를 사용하여 일련의 “few-shot 프롬프트”에 대한 성능에 따라 각 \(\alpha_k\)의 가능한 값을 검색한다. Few-shot 프롬프트는 나머지 테스트 프롬프트에서 선택되고 CEM의 모집단 샘플을 평가하는 데 사용된다. 여러 모집단 샘플이 동일한 점수를 얻는 경우 생성된 정답에서 가장 높은 평균 log-likelihood를 가진 샘플을 선택한다. 중요한 점은, 각 대상 task에 대해 이 프로세스를 한 번만 수행하면 되므로, 기존 few-shot prompting의 단점인 질문 프롬프트의 길이를 늘릴 필요가 없다.

Experiments

• Expert Task
  • 수학: GSM8K
  • 코딩: MBPP-pro
  • 추론: ARC-Easy
  • VLM: TextVQA
• Unseen Task
  • 수학: MATH
  • 코딩: Humaneval
  • 추론: ARC-Challenge
  • VLM: OKVQA

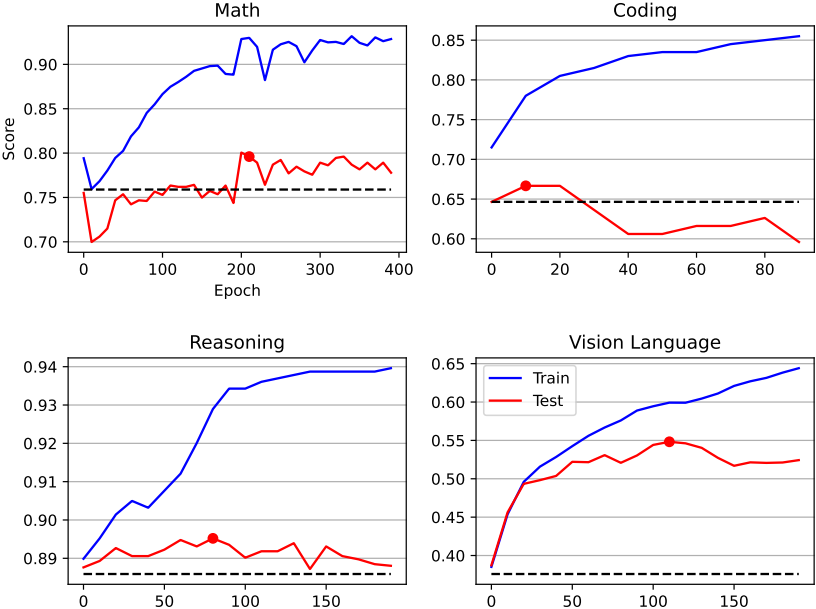
각 task에 대한 SVF learning curve는 아래와 같다.

1. Experimental Results

다음은 fine-tuning 결과이다.

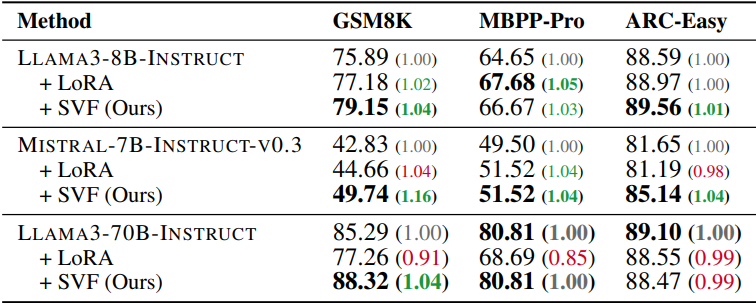
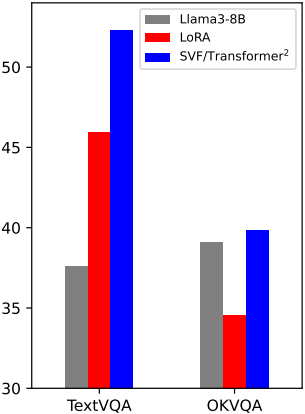
다음은 처음 보는 task에 대한 self-adaptation 성능을 비교한 표이다.

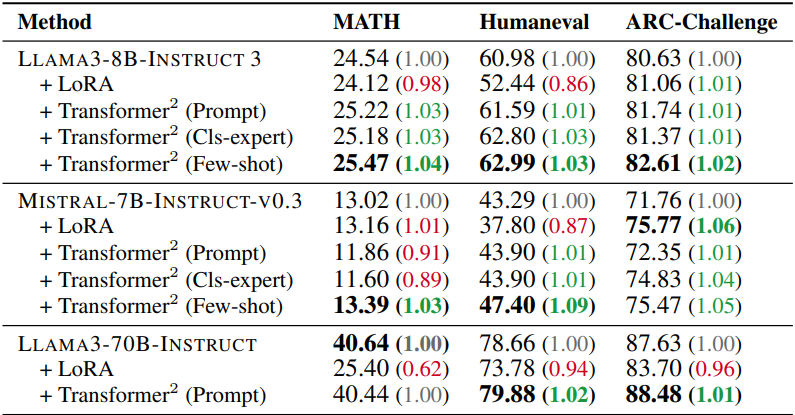
다음은 프롬프트 엔지니어링 전략을 사용할 때, 2단계 inference에 걸리는 시간을 비교한 표이다.

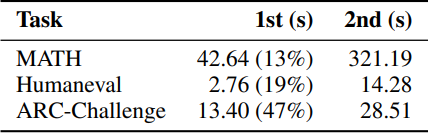
2. Analysis

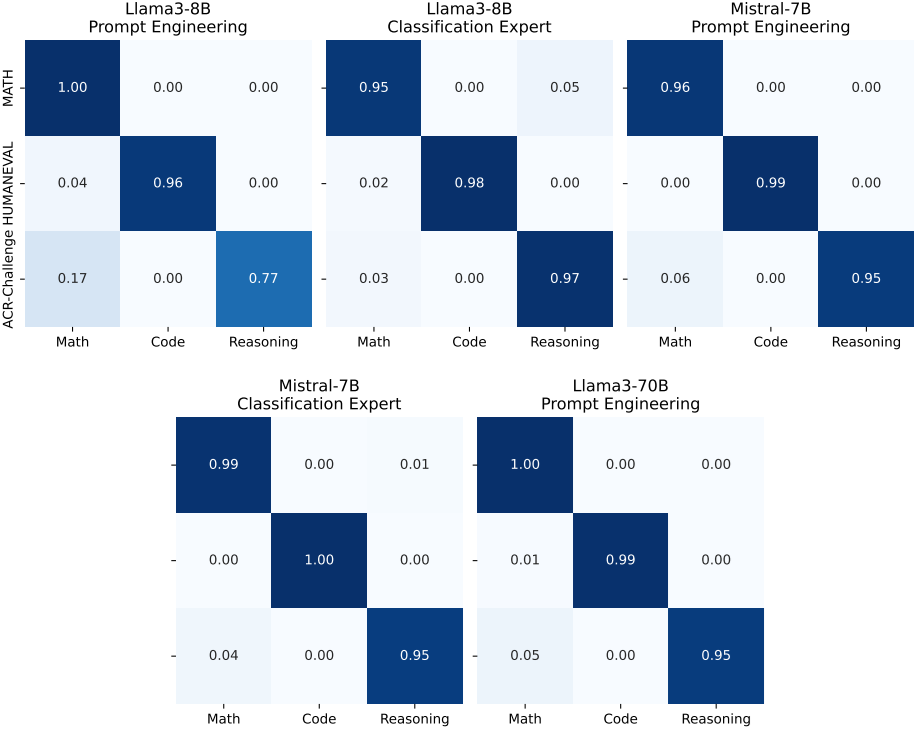
다음은 classification expert의 성능을 나타낸 것이다. 행은 실제 task 클래스이고, 열은 예측된 카테고리이다. 일부 샘플은 “Others”로 잘못 분류되어 합계가 1이 되지 않을 수 있다.

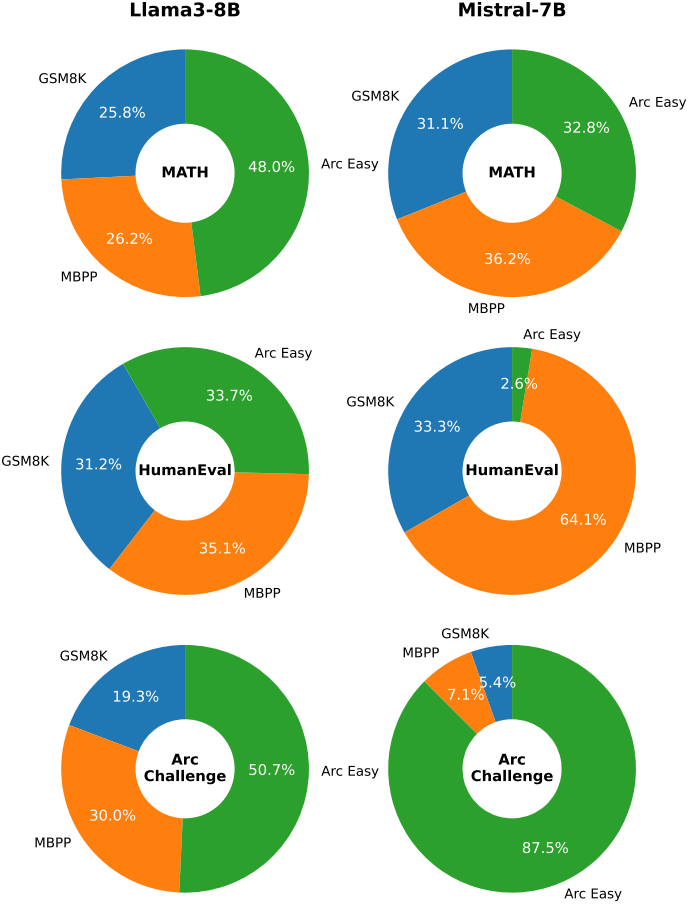
다음은 여러 벤치마크에 대하여 CEM으로 얻은 \(\alpha_k\)를 나타낸 그래프이다.

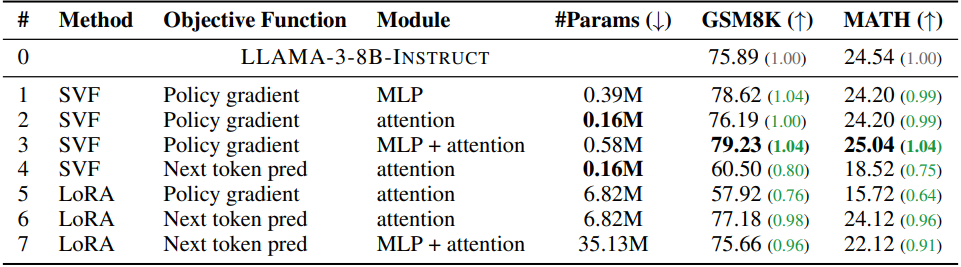
다음은 ablation study 결과이다. (Llama3-8B-Instruct, GSM8K)

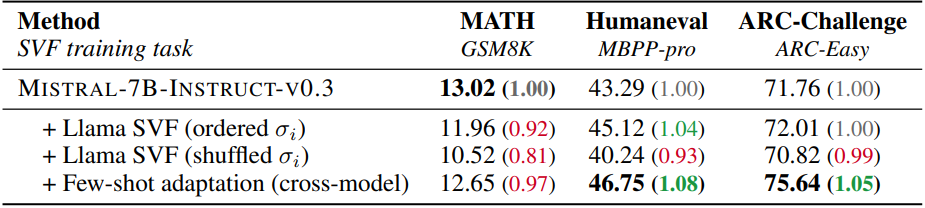
다음은 Llama3-8B-Instruct에서 학습된 expert 벡터들을 Mistral-7B-Instruct-v0.3에서 사용한 결과이다.