[논문리뷰] TokenFormer: Rethinking Transformer Scaling with Tokenized Model Parameters
ICLR 2025 (Spotlight). [Paper] [Page] [Github]
Haiyang Wang, Yue Fan, Muhammad Ferjad Naeem, Yongqin Xian, Jan Eric Lenssen, Liwei Wang, Federico Tombari, Bernt Schiele
Max Planck Institute for Informatics | Google | Peking University
30 Oct 2024
Introduction
Transformer는 일반적으로 하나의 토큰을 처리하는 데 필요한 계산을 두 가지 뚜렷한 부분으로 나눈다.
- 토큰-토큰 상호 작용: 다른 입력 토큰과의 상호 작용
- 토큰-파라미터 상호 작용: 모델 파라미터와 관련된 계산
Attention 메커니즘은 토큰-토큰 상호 작용을 용이하게 하여 최신 foundation model이 멀티모달 데이터를 통합 토큰 시퀀스로 인코딩하고 이들 간의 복잡한 의존성을 효과적으로 캡처할 수 있도록 한다. 반대로 토큰-파라미터 계산은 입력 토큰을 고정된 파라미터 집합으로 곱하는 linear projection에 크게 의존한다.
이러한 디자인은 모델 크기를 늘리려면 핵심 아키텍처 구성 요소를 변경해야 하며, 종종 전체 모델을 처음부터 다시 학습해야 하기 때문에 확장성이 제한된다. 모델이 커질수록 과도한 리소스 소비가 발생하여 점점 비실용적이 된다.
본 논문에서는 토큰-토큰 상호 작용과 토큰-파라미터 상호 작용을 모두 attention 메커니즘을 사용하여 통합하는 새로운 아키텍처인 Tokenformer를 소개한다. 이를 통해 토큰-파라미터 상호 작용의 유연성을 향상시키고, 모델 파라미터의 incremental scaling을 허용하며, 이전에 학습된 모델을 효과적으로 재사용하여 학습 부담을 크게 줄인다. 토큰-파라미터 attention layer의 유연성과 가변적인 수의 파라미터를 처리할 수 있는 능력은 본질적으로 모델의 확장성을 향상시켜 점진적으로 효율적인 스케일링을 용이하게 한다.
입력 토큰 간의 계산 패턴을 보존하고 cross-attention 메커니즘을 사용하여 모든 linear projection을 재구성함으로써 Transformer 아키텍처를 확장한다. 구체적으로, 입력 차원과 출력 차원이 각각 $D_1$, $D_2$인 feature를 projection하기 위해, 각각 채널 차원이 $D_1$과 $D_2$인 $N$개의 학습 가능한 토큰으로 구성된 두 개의 파라미터 세트를 사용한다. 여기서 입력 토큰은 query 역할을 하고 모델 파라미터는 key와 value로 작용한다. 이러한 유연성 덕분에 모델의 파라미터는 변수 $N$으로 본질적으로 확장 가능하여 새로운 key-value 파라미터 쌍을 지속적으로 추가하여 효율적으로 확장할 수 있다.
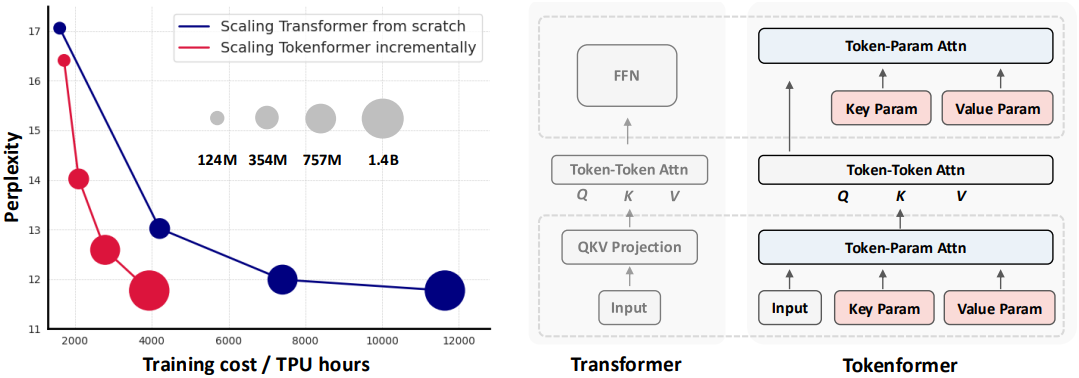
TokenFormer는 학습 비용의 절반 이상을 절약하면서 처음부터 학습하는 것과 유사한 성능을 달성하였다.
Method
1. TokenFormer
Transformer는 다양한 도메인에서 뛰어나지만, 확장성은 지정된 토큰-파라미터 상호작용(즉, linear projection)으로 인한 높은 계산 오버헤드로 제한된다. 결과적으로, 채널 차원과 같은 아키텍처 구성 요소를 조정하는 스케일링 전략은 처음부터 전체 모델을 다시 학습해야 하기 때문에 계산 리소스를 비효율적으로 사용하게 된다.
이러한 과제를 극복하기 위해, 본 논문은 전적으로 attention 메커니즘에 기반한 아키텍처인 Tokenformer를 제안하였다. Tokenformer의 핵심은 token-Parameter attention (Pattention) layer로, 모델 파라미터로 기능하는 일련의 학습 가능한 토큰을 통합한 다음 cross-attention을 사용하여 입력 토큰과 파라미터 토큰 간의 상호 작용을 관리한다.
이런 방식으로 Pattention layer는 입력 및 출력 채널 차원과 독립적으로 작동하는 추가 차원(파라미터 토큰 수)을 도입한다. 이러한 분리를 통해 입력 데이터는 가변적인 수의 파라미터와 동적으로 상호 작용할 수 있으므로 사전 학습된 모델을 재사용하여 incremental model scaling에 필요한 유연성을 제공한다. 결과적으로 더 큰 모델의 학습이 크게 가속화되는 동시에 처음부터 학습된 Transformer와 동일한 성능을 달성한다.
Pattention Layer
입력 토큰과 출력 토큰을 $\mathcal{I} \in \mathbb{R}^{T \times d_1}$ 및 $\mathcal{O} \in \mathbb{R}^{T \times d_2}$로 표현하자. 여기서 $T$는 시퀀스 길이이고 $d_1$과 $d_2$는 각각 입력과 출력의 차원이다.
Pattention 메커니즘을 구현하기 위해 학습 가능한 파라미터 토큰이 각각 $n$개인 두 세트를 도입한다. 하나는 key를 나타내는 $K_P \in \mathbb{R}^{n \times d_1}$이고, 다른 하나는 value를 나타내는 $V_P \in \mathbb{R}^{n \times d_2}$이다. Pattention layer의 출력 $\mathcal{O}$는 다음과 같이 계산된다.
\[\begin{equation} \textrm{Pattention} (X, K_P, V_P) = \Theta (X \cdot K_P^\top) \cdot V_P \end{equation}\]여기서 $\Theta$는 Pattention layer의 안정적인 최적화를 위한 수정된 softmax 연산이다. 출력 Pattention score $S \in \mathbb{R}^{n \times n}$는 다음과 같다.
\[\begin{equation} S_{ij} = f \bigg( \frac{A_{ij} \times \tau}{\sqrt{\sum_{k=1}^n \vert A_{ik} \vert^2}} \bigg), \quad \forall i, j \in 1 \ldots n \end{equation}\]여기서 $A$는 $(X \cdot K_P^\top)$에서 파생된 score이고, $\tau$는 기본적으로 $\sqrt{n}$으로 설정되는 scale factor이며, $f$는 GeLU 함수이다. 이 디자인은 아키텍처의 gradient 안정성을 개선하고 표준 softmax 연산에 비해 더 나은 성능을 제공한다.
Pattention layer는 토큰과 파라미터 간의 상호작용을 관리하기 위해 cross-attention 메커니즘을 사용하여 attention 메커니즘의 적응성 특성을 완전히 보존한다. Transformer 모델의 self-attention이 가변 길이의 시퀀스를 처리하는 방식과 유사하게, Pattention layer는 feature projection에 사용된 입력 및 출력 채널 차원과 무관하게 유연한 수의 파라미터를 처리하도록 설계되었다. 이를 통해 네트워크 파라미터를 파라미터 토큰 축을 따라 원활하게 확장하여 사전 학습된 가중치를 효과적으로 재사용하고 자연스럽게 점진적으로 모델을 스케일링할 수 있다.
Overall Architecture
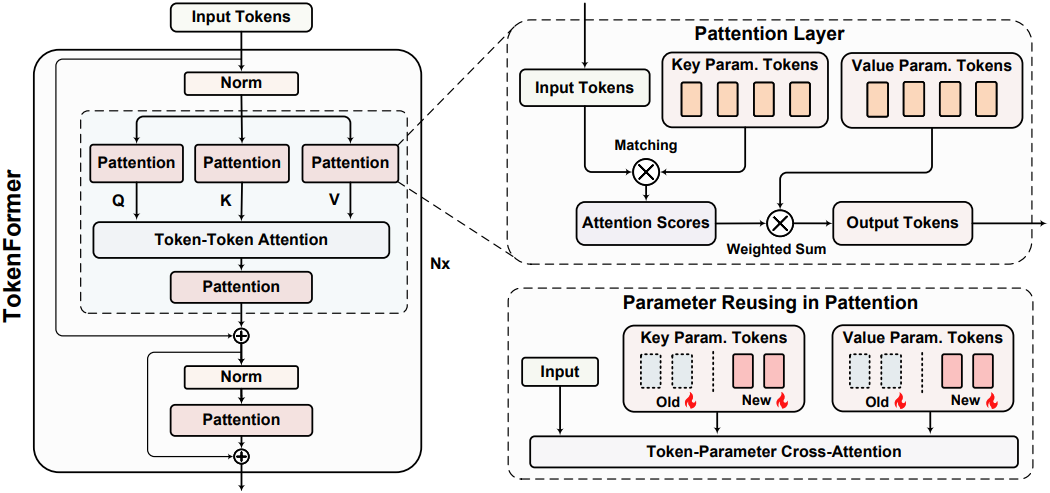
위 그림은 Tokenformer의 아키텍처를 보여준다. 입력 토큰 \(X_\textrm{in} \in \mathbb{R}^{T \times d}\)이 주어지면 pre-norm transformer의 디자인을 따르고 Tokenformer layer의 출력에 대한 계산은 다음과 같이 표현된다.
(LN은 layer normalization, MHA와 FFN은 각각 수정된 multi-head self-attention과 feed-forward layer)
Multi-head self-attention block에서는 단순성을 위해 하나의 head로 변경하고 $d_k$와 $d_v$를 모두 $d$와 같게 설정한다. 그런 다음 모든 linear projection을 Pattention layer로 대체한다. $\textrm{LN}(X_\textrm{in})$을 $X$로 표시하면 이 블록은 다음과 같이 공식화된다.
\[\begin{aligned} Q &= \textrm{Pattention} (X, K_P^Q, V_P^Q) \\ K &= \textrm{Pattention} (X, K_P^K, V_P^K) \\ V &= \textrm{Pattention} (X, K_P^V, V_P^V) \\ X_\textrm{attn} &= \textrm{softmax} \bigg[ \frac{Q \cdot K^\top}{\sqrt{d}} \bigg] \cdot V \\ O_\textrm{attn} &= \textrm{Pattention} (X_\textrm{attn}, K_P^O, V_P^O) \end{aligned}\]QKV projection의 key-value 파라미터 토큰은 $(K_P^Q, V_P^Q) \in \mathbb{R}^{n_q \times d}$, $(K_P^K, V_P^K) \in \mathbb{R}^{n_k \times d}$, $(K_P^V, V_P^V) \in \mathbb{R}^{n_v \times d}$이고, $(K_P^O, V_P^O) \in \mathbb{R}^{n_o \times d}$는 출력 projection layer에 사용된다.
일관성과 단순성을 위해 Tokenformer의 feed-forward block은 하나의 Pattention Layer를 활용한다. \(\textrm{LN}(X_\textrm{inter})\)를 \(X_\textrm{ffn}\)라 하면, FFN 계산은 다음과 같다.
\[\begin{equation} O_\textrm{ffn} = \textrm{Pattention} (X_\textrm{ffn}, K_P^\textrm{ffn}, V_P^\textrm{ffn}) \end{equation}\]여기서 \((K_P^\textrm{ffn}, V_P^\textrm{ffn}) \in \mathbb{R}^{n_\textrm{ffn} \times d}\)는 FFN block에 대한 학습 가능한 key-value 쌍이다.
이런 방식으로 아키텍처를 설계함으로써, 입력 데이터와 모델 파라미터를 포함한 모든 기본 구성 요소를 계산 프레임워크 내의 토큰으로 표현한다. 이 토큰 중심의 관점은 토큰-토큰 및 토큰-파라미터 상호 작용을 통합하여 뛰어난 유연성을 특징으로 하는 완전한 attention 기반 신경망을 구축할 수 있다.
Architecture Configurations
TokenFormer는 표준 Transformer 아키텍처의 hyperparameter 구성을 세심하게 반영하였다. 동일한 layer 수와 hidden dimension을 사용하며, query, key, value 및 출력 projection 모두에서 key-value 파라미터 쌍의 수는 hidden dimension에 직접 대응한다. 반면, FFN 모듈은 hidden size에 비해 4배 많은 파라미터 쌍을 사용한다.
이러한 아키텍처 정렬은 사전 학습된 Transformer를 사용하여 모델의 파라미터를 초기화하는 것을 용이하게 하여 Transformer 사전 학습 생태계에 원활하게 통합할 수 있도록 한다.
2. Progressive Model Scaling
TokenFormer는 Pattention 레이어의 변경하기 쉬운 디자인 덕분에 파라미터 축을 따라 대규모 모델 학습에 강한 적합성을 보인다. 이 디자인은 더 작은 사전 학습된 모델의 파라미터를 재사용하여 점진적으로 더 큰 모델을 개발할 수 있도록 한다.
일반성을 잃지 않고 쉬운 이해를 위해 하나의 Pattention layer를 사용한 모델 스케일링을 살펴보자. 사전 학습된 key-value 파라미터 토큰 세트 \(K_P^\textrm{old}, V_P^\textrm{old} \in \mathbb{R}^{n \times d}\)가 장착된 Tokenformer 모델을 확장하기 위해 새로운 key-value 파라미터 토큰 \(K_P^\textrm{new}, V_P^\textrm{new} \in \mathbb{R}^{m \times d}\)를 추가한다.
\[\begin{equation} K_P^\textrm{scale} = [K_P^\textrm{old}, K_P^\textrm{new}], \quad V_P^\textrm{scale} = [V_P^\textrm{old}, V_P^\textrm{new}] \end{equation}\]($[\cdot^\textrm{old}, \cdot^\textrm{new}]$는 토큰 차원으로의 concat 연산, \(K_P^\textrm{scale}, V_P^\textrm{scale} \in \mathbb{R}^{(m+n) \times d}\)는 스케일링된 파라미터 집합)
스케일링된 모델의 forward pass는 다음과 같이 정의된다.
\[\begin{equation} O = \textrm{Pattention} (X, K_P^\textrm{scale}, V_P^\textrm{scale}) \end{equation}\]이 스케일링 방식은 입력 또는 출력 차원을 변경하지 않고 임의의 수의 파라미터를 통합할 수 있도록 한다. 이 접근 방식은 성능을 저하시키지 않고 더 큰 스케일에서 모델의 학습 효율성을 현저히 향상시킨다.
LoRA와 유사하게 \(K_P^\textrm{new}\)를 0으로 초기화함으로써, 모델은 잘 학습된 지식을 잃지 않고 사전 학습 단계의 모델 상태를 완벽하게 재개할 수 있어 더 빠른 수렴을 용이하게 하고 전반적인 스케일링 프로세스를 가속화할 수 있다.
Experiments
1. Progressive Model Scaling
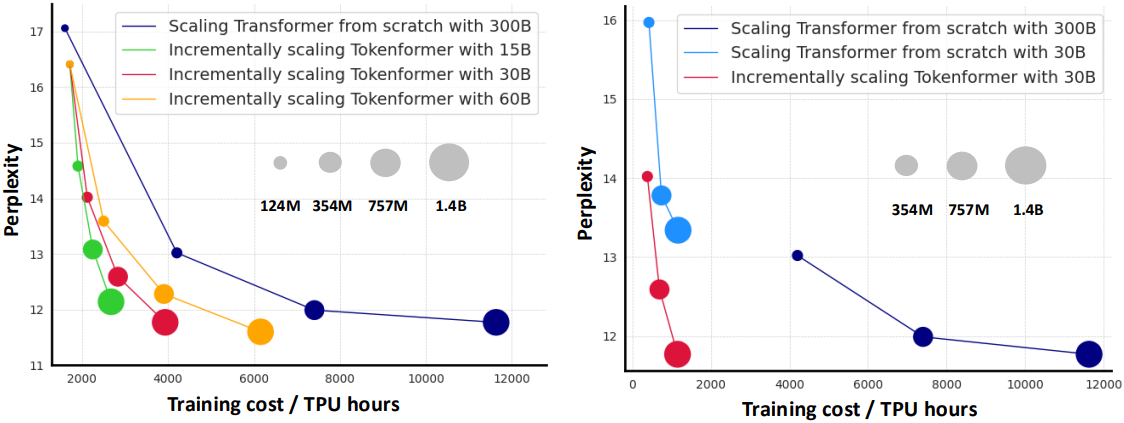
다음은 Transformer와 스케일링 비용을 비교한 그래프이다.
2. Benchmarking of Model Expressiveness
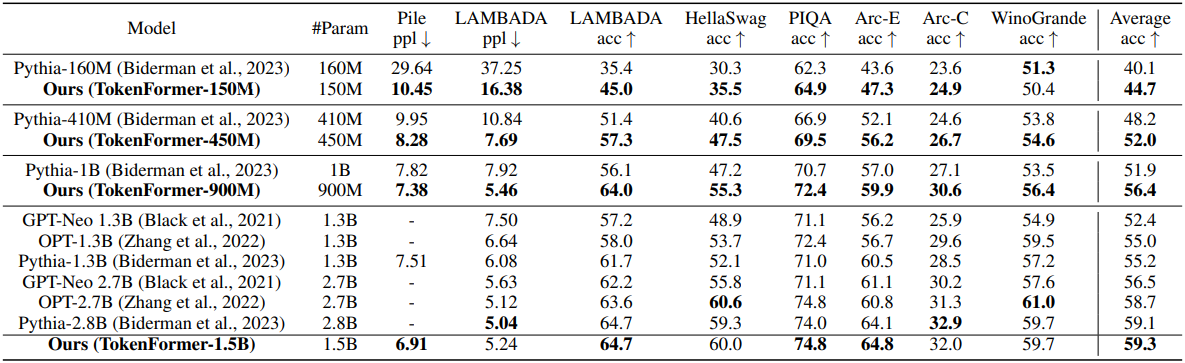
다음은 Transformer 기반의 언어 모델과 zero-shot 성능을 비교한 표이다.
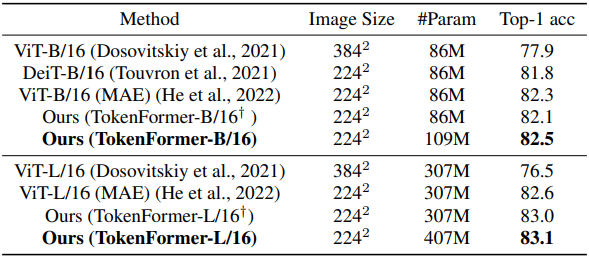
다음은 ViT와 ImageNet-1K classification 성능을 비교한 표이다.
3. Comparison with Standard Transformer
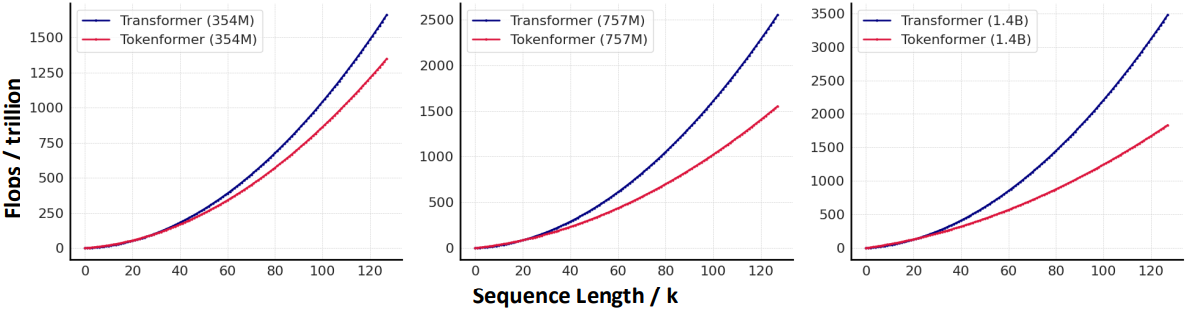
다음은 FLOPS와 텍스트 길이 사이의 관계를 비교한 그래프이다.
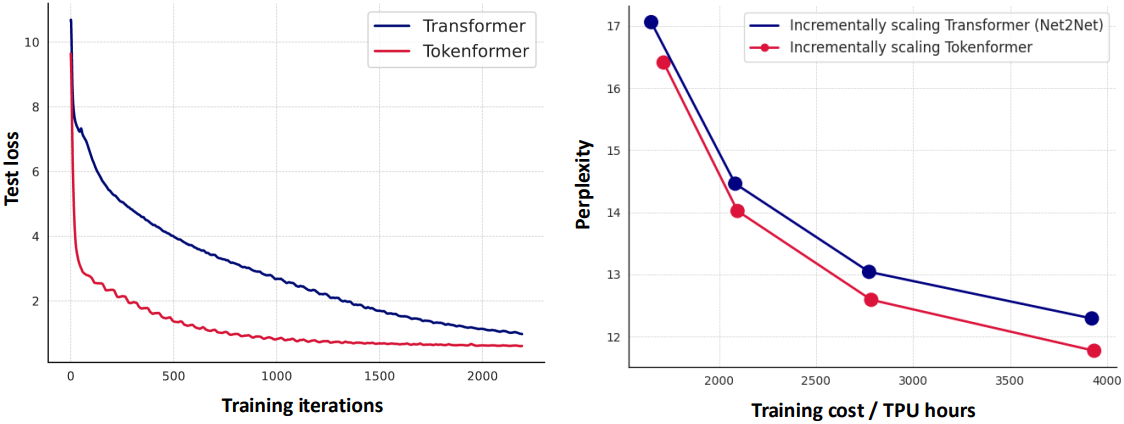
다음은 (왼쪽) loss curve와 (오른쪽) incremental model scaling의 성능을 비교한 그래프이다.
4. Ablation Study
다음은 (왼쪽) softmax와 (오른쪽) layer normalization에 대한 ablation 결과이다. (ImageNet classification)
