[논문리뷰] TinyFusion: Diffusion Transformers Learned Shallow

CVPR 2025. [Paper] [Github]
Gongfan Fang, Kunjun Li, Xinyin Ma, Xinchao Wang
National University of Singapore
2 Dec 2024

Introduction

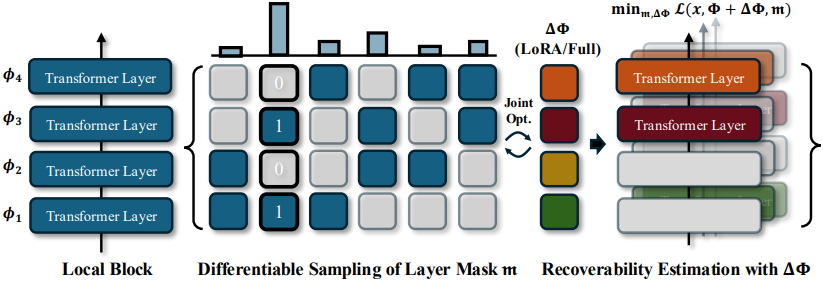
본 연구는 표준 depth pruning 프레임워크를 따라, DiT의 중요하지 않은 레이어를 먼저 제거한 후, pruning된 모델을 fine-tuning하여 성능을 회복한다. DiT fine-tuning은 매우 시간이 많이 소요되는 과정이다. 본 논문은 pruning 직후 loss를 최소화하는 모델을 찾는 대신, 우수한 복구성을 가진 후보 모델을 식별하여 fine-tuning 후 우수한 성능을 구현하는 방안을 제안하였다. 이 목표를 달성하는 것은 특히 어려운데, pruning과 fine-tuning이라는 두 가지 별개의 프로세스를 통합해야 하기 때문이다. 이 프로세스는 미분 불가능한 연산을 포함하며 gradient descent를 통해 직접 최적화할 수 없다.

이를 위해, pruning과 fine-tuning을 효과적으로 통합하는 학습 가능한 depth pruning 방법을 제안하였다. DiT의 pruning과 fine-tuning을 레이어 마스크의 미분 가능한 샘플링 과정으로 모델링하고, 이를 공동 최적화된 가중치 업데이트와 결합하여 향후 fine-tuning을 시뮬레이션한다. 본 논문의 목표는 이러한 분포를 반복적으로 개선하여 복구 가능성이 높은 네트워크가 샘플링될 가능성을 높이는 것이다. 이는 간단한 전략을 통해 달성된다. 샘플링된 pruning 결정이 강력한 복구 가능성을 가져오면, 유사한 pruning 패턴이 샘플링될 확률이 높아진다. 이 접근법은 덜 효과적인 해를 무시하고 잠재적으로 가치 있는 해를 탐색하는 데 도움이 된다. 또한, 제안된 방법은 매우 효율적이며, 몇 step의 학습만으로 적합한 해를 도출할 수 있다.

제안된 방법인 TinyFusion은 1-epoch 학습을 통해 DiT에서 중복 레이어를 식별할 수 있으며, 이를 통해 사전 학습된 모델에서 높은 복구율을 가진 얕은 DiT를 효과적으로 생성할 수 있다. 예를 들어, TinyFusion으로 pruning된 모델은 레이어의 50%를 제거한 후 초기에는 비교적 높은 loss를 보이지만 fine-tuning을 통해 빠르게 복구되어 사전 학습 비용의 1%만 사용하더라도 기존 방법에 비해 훨씬 더 경쟁력 있는 FID를 달성한다 (5.73 vs. 22.28).

또한 저자들은 MaskedKD 변형을 도입하여 복구율을 향상시키는 knowledge distillation의 역할도 탐구하였다. MaskedKD는 fine-tuning의 성능과 안정성에 상당한 영향을 미칠 수 있는 hidden state의 너무 큰 activation의 부정적인 영향을 완화한다. MaskedKD를 사용하면 사전 학습 비용의 1%만으로 FID 점수가 5.73에서 3.73으로 향상된다. 학습 비용을 사전 학습 비용의 7%로 확장하면 FID가 2.86으로 더욱 낮아지는데, 이는 깊이를 두 배로 늘린 원래 모델보다 0.4만 더 높은 수치이다.

Method

1. Shallow Generative Transformers by Pruning

본 연구는 사전 학습된 모델을 pruning하여 얕은 DiT를 만드는 것을 목표로 한다. \(\Phi_{L \times D} = [\phi_1, \cdots, \phi_L]^\top\)로 parameterize된 $L$-layer transformer를 고려하자. 여기서 각 \(\phi_i\)는 transformer layer의 모든 학습 가능한 파라미터를 $D$차원 열 벡터로 포함하며, 여기에는 attention layer와 MLP의 가중치가 모두 포함된다. Depth pruning은 다음과 같이 레이어를 제거하는 바이너리 레이어 마스크 \(\textbf{m}_{L \times 1} = [m_1, \cdots, m_L]^\top\)를 찾는 것이 목표이다.

\[\begin{equation} x_{i+1} = m_i \phi_i (x_i) + (1 - m_i) x_i = \begin{cases} \phi_i (x_i) & \textrm{if} \; m_i = 1 \\ x_i & \textrm{otherwise} \end{cases} \end{equation}\]

($x_i$와 \(\phi_i (x_i)\)는 각각 레이어 \(\phi_i\)의 입력과 출력)

마스크를 얻기 위해 기존의 일반적인 패러다임은 pruning 후 loss $\mathcal{L}$을 최소화하는 것이다.

\[\begin{equation} \min_\textbf{m} \mathbb{E}_x (\mathcal{L} (x, \Phi, \textbf{m})) \end{equation}\]

그러나 이 목적 함수는 DiT를 pruning하는 데 적합하지 않다. 대신, 저자들은 pruning된 모델의 복구 가능성에 더 관심이 있다. 이를 위해, 최적화 문제에 추가 가중치 업데이트를 통합하고 목적 함수를 다음과 같이 확장한다.

\[\begin{equation} \min_\textbf{m} \underbrace{\min_{\Delta \Phi} \mathbb{E}_x [\mathcal{L}(x, \Phi + \Delta \Phi, \textbf{m})]}_{\textrm{Recoverability: Post-Fine-Tuning Performance}} \end{equation}\]

(\(\Delta \Phi = \{\Delta \phi_1, \cdots, \Delta \phi_M\}\)은 fine-tuning을 통한 적절한 업데이트)

위 식은 두 가지 문제점이 존재한다.

1. 레이어 선택의 미분 불가능성으로 인해 gradient descent를 사용한 최적화가 불가능하다.
2. 선택된 모든 후보 모델에 대한 평가를 위해 fine-tuning이 필요하기 때문에 전체 탐색 공간을 탐색하는 것이 계산적으로 어렵다.

본 논문은 이 문제들을 해결하기 위해 pruning과 복구 가능성을 모두 최적화할 수 있는 TinyFusion을 제안하였다.

2. TinyFusion: Learnable Depth Pruning

확률론적 관점

본 논문은 확률론적 관점에서 위 식을 모델링한다. 이상적인 pruning 방법으로 생성된 마스크 $\textbf{m}$은 특정 분포를 따라야 한다고 가정한다. 이를 모델링하기 위해 가능한 모든 마스크 $\textbf{m}$을 확률 값 $p(\textbf{m})$과 연관시켜 카테고리 분포를 형성하는 것이 직관적이다. Pruning 마스크 평가는 균등 분포에서 시작된다. 그러나 이 초기 분포에서 직접 샘플링하는 것은 방대한 검색 공간으로 인해 매우 비효율적이다. 예를 들어, 28-layer 모델을 50% pruning하려면 40,116,600개의 가능한 모든 해를 평가해야 한다.

이러한 문제를 극복하기 위해, 본 논문에서는 평가 결과를 피드백으로 사용하여 마스크 분포를 반복적으로 개선할 수 있는 학습 알고리즘을 도입하였다. 기본 아이디어는 특정 마스크가 긍정적인 결과를 보일 경우, 유사한 패턴을 가진 다른 마스크도 잠재적인 해결책이 될 수 있으며, 따라서 후속 평가에서 샘플링될 가능성이 더 높아져 유망한 해에 대한 더욱 집중적인 탐색이 가능해진다는 것이다.

로컬 구조 샘플링

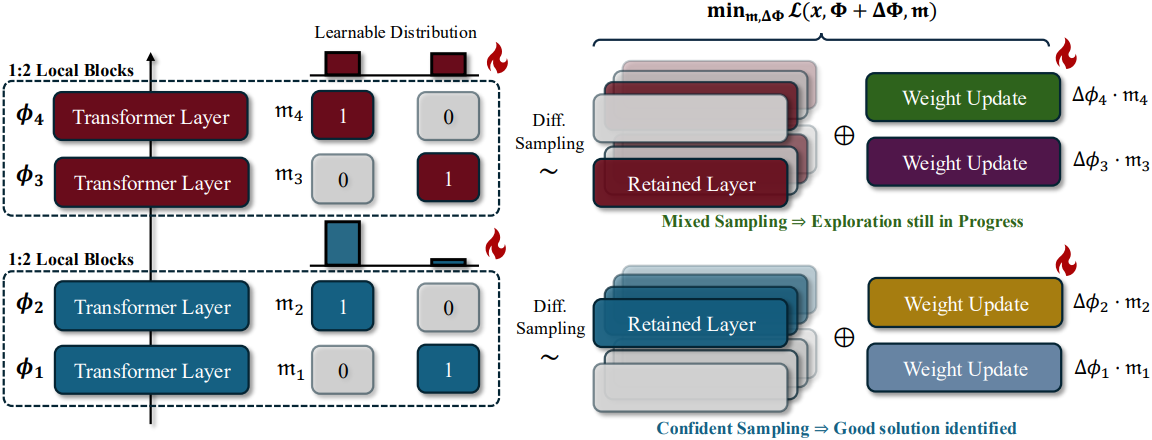
본 논문에서는 로컬 구조가 서로 다른 마스크 간의 관계를 모델링하는 효과적인 앵커 역할을 할 수 있음을 보여준다. Pruning 마스크가 특정 로컬 구조를 유도하고 fine-tuning 후 경쟁력 있는 결과를 도출한다면, 동일한 로컬 패턴을 생성하는 다른 마스크들도 긍정적인 해를 도출할 가능성이 높다. 이는 원래 모델을 $K$개의 겹치지 않는 블록 \(\Phi = [\Phi_1, \cdots, \Phi_K]^\top\)로 나누어 달성할 수 있다. 단순화를 위해 각 블록 \(\Phi_k = [\phi_{k1}, \cdots, \phi_{kM}]^\top\)은 정확히 $M$개의 레이어를 포함하지만, 각 레이어의 길이는 다를 수 있다고 가정한다.

저자들은 모든 레이어에 대하여 동시에 pruning하는 대신, $M$개의 레이어를 갖는 각 블록 \(\Phi_k\)에 대해 $N$개의 레이어를 유지하는 $N:M$ 방식의 local layer pruning을 제안하였다. 이를 통해 로컬 바이너리 마스크의 ​​집합 \(\textbf{m} = [\textbf{m}_1, \cdots, \textbf{m}_K]^\top\)를 얻을 수 있다. 마찬가지로, 로컬 마스크 \(\textbf{m}_k\)의 분포는 카테고리 분포 \(p(\textbf{m}_k)\)를 사용하여 모델링한다. 로컬 바이너리 마스크들을 독립적으로 샘플링하고 이를 결합하여 pruning을 수행한다.

\[\begin{equation} p(\textbf{m}) = p(\textbf{m}_1) \cdot p(\textbf{m}_2) \cdots p(\textbf{m}_K) \end{equation}\]

일부 로컬 분포 \(p(\textbf{m}_k)\)가 해당 블록에서 높은 신뢰도를 보이는 경우, 시스템은 해당 긍정적 패턴을 자주 샘플링하고 다른 로컬 블록에서 활발한 탐색을 유지하는 경향이 있다. 이러한 개념을 바탕으로, 본 논문에서는 미분 가능한 샘플링을 도입하여 위 과정을 학습 가능하게 만들었다.

미분 가능한 샘플링

로컬 블록 \(\phi_k\)에 대응하고 카테고리 분포 \(p(\textbf{m}_k)\)로 모델링되는 로컬 마스크 \(\textbf{m}_k\)의 샘플링 프로세스를 고려하자. $N:M$ 방식을 사용하면 $\binom{M}{N}$개의 가능한 마스크가 있다. 가능한 모든 마스크를 열거하기 위해 특수 행렬 \(\hat{\textbf{m}}^{N:M}\)을 구성한다. 예를 들어, 2:3 layer pruning은 후보 행렬 \(\hat{\textbf{m}^{2:3}} = [[1, 1, 0], [1, 0, 1], [0, 1, 1]]\)을 생성한다. 이 경우 각 블록은 세 가지 확률 \(p(\textbf{m}_k) = [p_{k1}, p_{k2}, p_{k3}]\)을 갖는다. 단순화를 위해 $k$를 생략하고, \(\hat{\textbf{m}}^{N:M}\)의 $i$번째 element를 샘플링할 확률 $p_i$로 나타내자. 샘플링 프로세스를 미분 가능하게 만드는 널리 사용되는 방법은 Gumbel-Softmax이다.

\[\begin{equation} y = \textrm{one-hot} \left( \frac{\exp ((g_i + \log p_i) / \tau)}{\sum_j \exp ((g_j + \log p_j) / \tau)} \right), \quad \textrm{where} \; g_i \sim \textrm{Gumbel}(0, 1) \end{equation}\]

($\tau$는 temperature, $y$는 샘플링된 마스크의 인덱스)

One-hot 연산에 Straight-Through Estimator (STE)가 적용되어, forward에서는 one-hot 연산이 활성화되고 backward에서는 항등 함수로 처리된다. One-hot 인덱스 $y$와 후보 집합 \(\hat{\textbf{m}}^{N:M}\)을 활용하여 간단한 인덱스 연산을 통해 마스크 $\textbf{m} \sim p(\textbf{m})$을 도출할 수 있다.

\[\begin{equation} \textbf{m} = y^\top \hat{\textbf{m}} \end{equation}\]

특히, $\tau \rightarrow 0$일 때 STE gradient는 실제 gradient에 근접하지만, 분산이 더 높아져 학습에 부정적인 영향을 미친다. 따라서 일반적으로 scheduler를 사용하여 높은 $\tau$로 학습을 시작한 후 시간이 지남에 따라 점진적으로 $\tau$를 낮춘다.

복구 가능성을 고려한 공동 최적화

Gradient descent를 사용하여 확률을 업데이트하여 샘플링된 마스크의 복구 가능성을 최대화한다. 학습 가능한 분포를 통합하여 목적 함수를 재구성한다.

\[\begin{equation} \min_{\{p(\textbf{m}_k)\}} \underbrace{\min_{\Delta \Phi} \mathbb{E}_{x, \{\textbf{m}_k \sim p(\textbf{m}_k)\}} [\mathcal{L}(x, \Phi + \Delta \Phi, \{\textbf{m}_k\})]}_{\textrm{Recoverability: Post-Fine-Tuning Performance}} \end{equation}\]

이 식을 기반으로 분포와 가중치 업데이트 $\Delta \Phi$를 공동으로 최적화한다. 가중치를 업데이트하는 간단한 방법은 원래 네트워크를 직접 최적화하는 것이지만, DiT는 파라미터가 매우 많기 때문에 전체 최적화는 학습 프로세스에 비용이 많이 들고 효율적이지 않을 수 있다. 따라서 LoRA를 사용하여 다음과 같이 $\Delta \Phi$를 얻고, 다음과 같이 fine-tuning을 시뮬레이션한다.

\[\begin{equation} \textbf{W}_\textrm{fine-tuned} = \textbf{W} + \alpha \Delta \textbf{W} = \textbf{W} + \alpha \textbf{BA} \end{equation}\]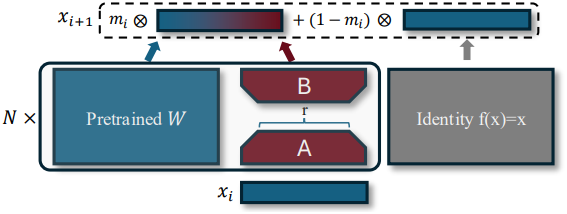

LoRA를 사용하면 파라미터 수가 크게 줄어들어 다양한 pruning 결정에 대한 효율적인 탐색이 용이해진다. 샘플링된 바이너리 마스크 ​​값 $m_i$를 게이트로 사용하여 네트워크를 전달한다.

또한, STE는 pruning된 레이어에 0이 아닌 gradient를 제공하여 추가 업데이트가 가능하도록 한다. 이는 실제로 도움이 되는데, 일부 레이어는 처음에는 경쟁력이 없더라도 충분한 fine-tuning을 통해 경쟁력 있는 후보로 부상할 수 있기 때문이다.

Pruning 결정

학습 후, 가장 높은 확률을 갖는 로컬 구조를 유지하고 추가 업데이트 $\Delta \Phi$를 삭제한다. 그런 다음, 표준 fine-tuning 기법을 적용하여 복구한다.

Experiments

• Task: ImageNet 256$\times$256에 대한 클래스 조건부 이미지 생성

1. Results on Diffusion Transformers

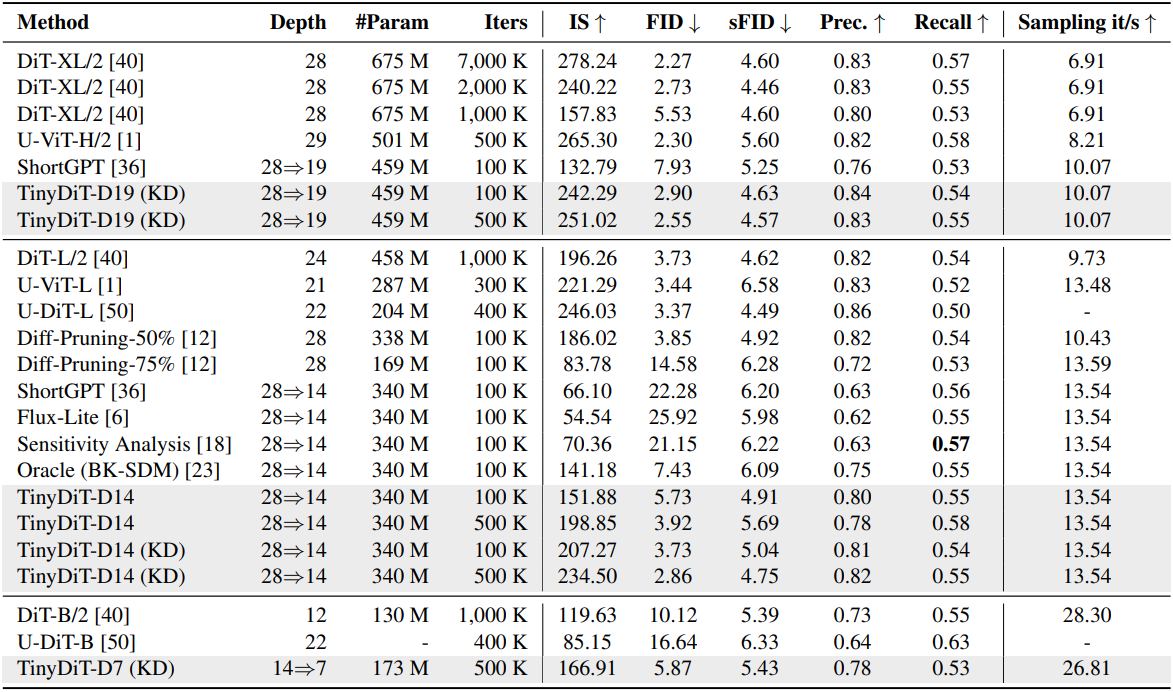
다음은 DiT-XL/2에 대한 layer pruning 결과이다.

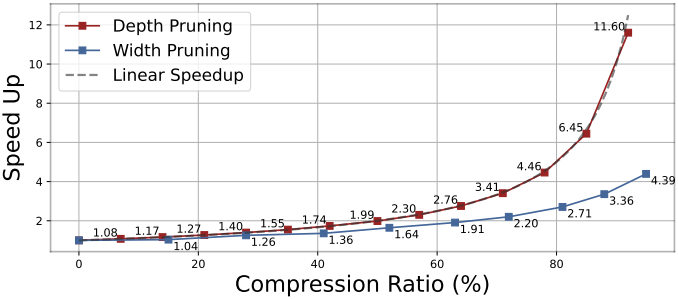
다음은 depth pruning과 width pruning의 성능을 비교한 그래프이다. 압축 비율이 증가함에 따라 depth pruning은 이론적인 선형적인 속도 향상과 밀접하게 일치한다.

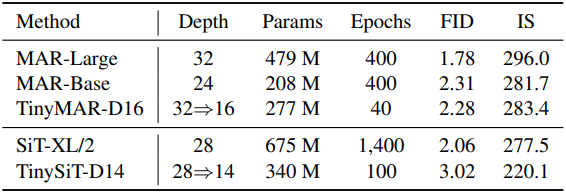
다음은 MAR과 SiT에 대한 layer pruning 결과이다.

2. Analytical Experiments

다음은 후보 모델을 랜덤 샘플링했을 때, calibration loss의 분포를 나타낸 그래프이다.

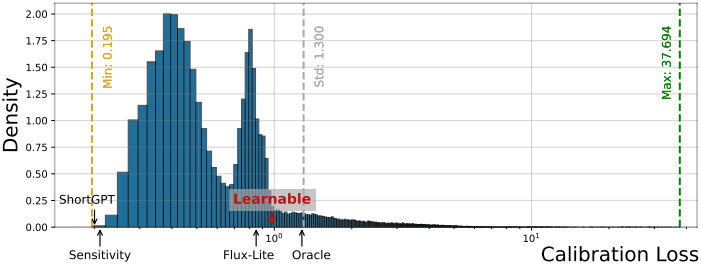
다음은 pruning 전략에 대한 비교 결과이다. Calibration loss가 작은 모델이 최선이 아님을 보여준다.

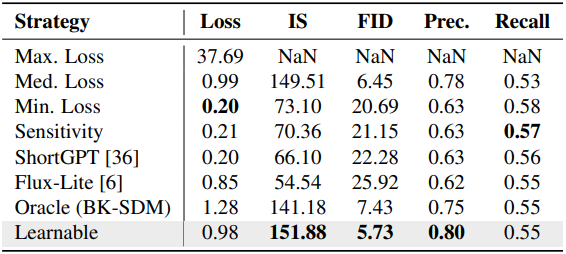
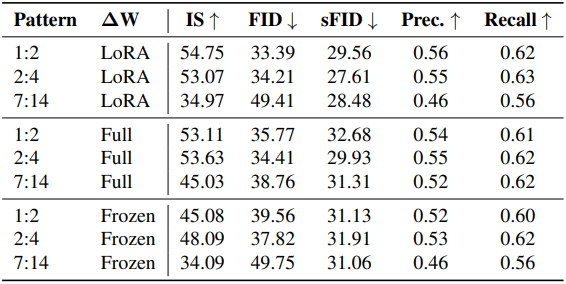
다음은 pruning 패턴과 복구 가능성 평가 전략에 대한 성능 비교 결과이다.

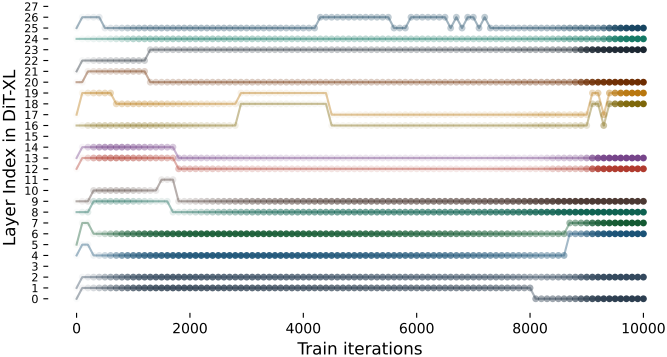
다음은 2:4 방식에서 어떤 레이어가 각 블록에서 선택되는 지를 시각화한 그래프이다. (투명도: 신뢰도 수준)

3. Knowledge Distillation for Recovery

다음은 teacher와 student에 대한 hidden state의 activation 값을 나타낸 그래프이다. DiT는 극단적인 activation 값을 가지고 있기 때문에 activation 값을 바로 distillation하는 것은 학습을 불안정하게 만든다.

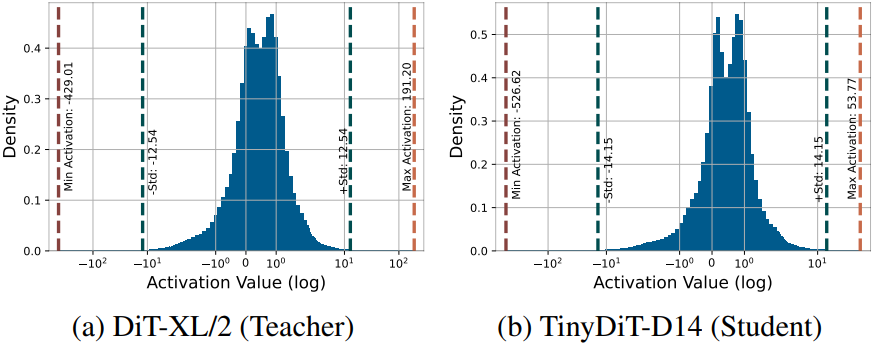
이 문제를 해결하기 위해, 저자들은 지식 전달 과정에서 이러한 극단적인 activation을 선택적으로 배제하는 Masked RepKD을 제안하였다. 간단하게 \(\vert x − \mu_x \vert < k \sigma_x\)로 thresholding하여 극단적인 activation과 관련된 loss를 무시한다.

다음은 복구를 위한 fine-tuning 전략을 비교한 표이다.

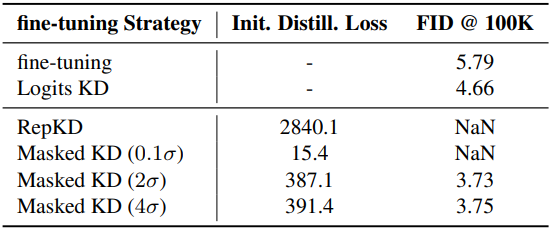
다음은 DiT-XL/2에서 pruning하고 distillation한 TinyDiT-D14로 생성한 이미지들이다.