[논문리뷰] TensoRF: Tensorial Radiance Fields

ECCV 2022. [Paper] [Page] [Github]
Anpei Chen, Zexiang Xu, Andreas Geiger, Jingyi Yu, Hao Su
ShanghaiTech University | Adobe Research | University of Tübingen | MPI-IS | UC San Diego
17 Mar 2022

Introduction

최근 NeRF와 많은 후속 연구들은 장면을 radiance field로 모델링하는 데 성공했으며 사실적인 렌더링이 가능하다. MLP 기반 NeRF 모델은 적은 메모리가 필요하지만 학습시키는 데 오랜 시간이 걸린다.

본 논문에서는 매우 컴팩트하고 빠르게 재구성할 수 있는 새로운 radiance field 표현인 TensoRF를 제안하였으며, SOTA 렌더링 품질을 달성하였다. NeRF에서 사용되는 좌표 기반 MLP와 달리, radiance field를 명시적인 feature voxel grid로 표현한다. Feature grid는 해상도의 세제곱에 비례하여 크기가 커지므로 대용량의 GPU 메모리가 필요하고, 일부는 distillation을 위해 NeRF를 미리 계산해야 하기 때문에 재구성 시간이 매우 길어진다.

저자들은 feature grid를 4D 텐서로 볼 수 있다는 사실을 활용하여 feature grid 표현의 비효율성을 해결하였다. 여기서 3개의 차원은 그리드의 XYZ 축에 해당하고 4번째 차원은 feature 차원이다. 이를 통해 고전적인 tensor decomposition 기술을 radiance field 모델링에 활용할 수 있게 되었다. 따라서 radiance field의 텐서를 여러 개의 low-rank 텐서 성분으로 분해하여 정확하고 컴팩트한 장면 표현을 도출할 수 있다. Radiance field를 텐서화한다는 본 논문의 핵심 아이디어는 일반적이며 모든 tensor decomposition 기술에 채택될 수 있다.

저자들은 먼저 고전적인 CANDECOMP/PARAFAC (CP) decomposition을 시도하였다. CP decomposition을 사용한 TensoRF는 사실적인 렌더링을 달성할 수 있고 MLP 기반인 NeRF보다 더 컴팩트한 모델을 만들어낼 수 있다. 그러나 복잡한 장면의 재구성 품질을 더욱 높이기 위해 더 많은 성분을 사용해야 하며, 이는 학습 시간을 증가시킨다.

따라서 저자들은 동일한 표현 용량에 필요한 성분 수를 효과적으로 줄여 더 빠른 재구성과 더 나은 렌더링으로 이어지는 새로운 vector-matrix (VM) decomposition을 제안하였다. 벡터들의 외적의 합을 사용하는 CP decomposition과 달리 VM decomposition은 벡터-행렬 외적의 합을 고려하였다. 본질적으로 행렬로 두 차원을 공동으로 모델링하여 각 성분의 rank를 완화한다. 이렇게 하면 CP decomposition에 비해 모델 크기가 커지지만 각 성분이 더 높은 rank의 더 복잡한 텐서 데이터를 표현할 수 있으므로 모델링에서 필요한 성분 수를 크게 줄일 수 있다.

CP/VM decomposition을 통해 voxel grid에서 공간적으로 변하는 feature를 컴팩트하게 인코딩한다. Volume density와 뷰에 따른 색상은 feature에서 디코딩될 수 있으며, 이는 볼륨 렌더링을 지원한다. 연속적인 field를 모델링하기 위해 discrete한 표현에 효율적인 trilinear interpolation을 사용하였다.

이 표현은 다양한 디코딩 함수에 사용할 수 있는 다양한 유형의 feature를 지원한다. MLP를 사용하기 위해 neural feature를 사용할 수도 있으며, spherical harmonics (SH)를 사용하기 위해 SH 계수를 사용할 수도 있다. SH 계수를 사용하는 경우, 고정된 SH 함수를 통해 간단한 색상 계산이 가능하고 신경망 없이 표현 가능하게 된다.

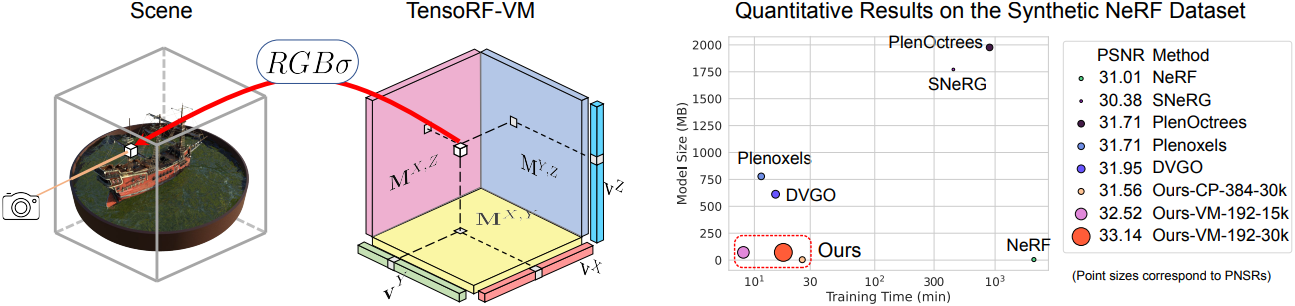
Voxel grid를 직접 재구성하면 공간 복잡도가 $O(N^3)$이지만, CP decomposition을 사용하면 $O(N)$, VM decomposition을 사용하면 $O(N^2)$으로 메모리 복잡도가 줄어든다. TensoRF는 low-rank regularization을 통해 높은 렌더링 품질을 제공하며, 모든 모델이 30분 안에 고품질의 radiance field를 재구성할 수 있다. 특히, VM decomposition을 사용한 모델은 재구성에 10분도 걸리지 않아 NeRF보다 약 100배 빠르며 훨씬 적은 메모리를 필요로 한다.

CP and VM Decomposition

(왼쪽: CP decomposition, 오른쪽: VM decomposition)

CP decomposition

3차원 텐서 $\mathcal{T} \in \mathbb{R}^{I, J, K}$가 주어지면 CP decomposition은 $\mathcal{T}$를 벡터의 외적의 합으로 분해한다.

\[\begin{equation} \mathcal{T} = \sum_{r=1}^R \textbf{v}_r^1 \circ \textbf{v}_r^2 \circ \textbf{v}_r^3 \end{equation}\]

여기서 \(\textbf{v}_r^1 \in \mathbb{R}^I\), \(\textbf{v}_r^2 \in \mathbb{R}^J\), \(\textbf{v}_r^3 \in \mathbb{R}^K\)은 $r$번째 성분의 분해된 벡터이며, $\circ$는 외적을 의미한다. 따라서 각 \(\mathcal{T}_{ijk}\)는 스칼라 곱의 합이다.

\[\begin{equation} \mathcal{T}_{ijk} = \sum_{r=1}^R \textbf{v}_{r,i}^1 \textbf{v}_{r,j}^2 \textbf{v}_{r,k}^3 \end{equation}\]

CP decomposition은 텐서를 여러 벡터로 분해하여 여러 개의 rank가 1인 성분을 컴팩트하게 표현한다. CP는 radiance field 모델링에 직접 적용하여 고품질 결과를 생성할 수 있지만, 너무 컴팩트하여 복잡한 장면을 모델링하는 데 많은 성분이 필요할 수 있으며, 재구성에 높은 계산 비용이 발생할 수 있다.

Vector-Matrix (VM) decomposition

벡터들을 활용하는 CP decomposition과 달리 VM decomposition은 텐서를 여러 벡터와 행렬로 분해한다.

\[\begin{equation} \mathcal{T} = \sum_{r=1}^{R_1} \textbf{v}_r^1 \circ \textbf{M}_r^{2,3} + \sum_{r=1}^{R_2} \textbf{v}_r^2 \circ \textbf{M}_r^{1,3} + \sum_{r=1}^{R_3} \textbf{v}_r^3 \circ \textbf{M}_r^{1,2} \end{equation}\]

여기서 \(\textbf{M}_r^{2,3} \in \mathbb{R}^{J \times K}\), \(\textbf{M}_r^{1,3} \in \mathbb{R}^{I \times K}\), \(\textbf{M}_r^{1,2} \in \mathbb{R}^{I \times J}\)는 2가지 차원을 나타내는 행렬이다. CP에서 별도의 벡터를 사용하는 대신 두 차원을 하나의 행렬로 표현하여 각 차원이 더 적은 수의 성분으로 적절하게 표현될 수 있도록 한다. $R_1$, $R_2$, $R_3$는 서로 다르게 설정할 수 있으며 각 차원의 복잡도에 따라 선택해야 한다.

VM decomposition의 각 성분은 CP decomposition의 성분보다 더 많은 파라미터를 가지고 있다. 이로 인해 압축성이 낮아지지만 더 복잡한 고차원 데이터를 표현할 수 있으므로 동일한 복잡한 함수를 모델링할 때 필요한 성분 수가 줄어든다. VM decomposition은 여전히 매우 높은 압축성을 가지고 있어 voxel grid 표현과 비교했을 때 메모리 복잡도가 $O(N^3)$에서 $O(N^2)$로 줄어든다.

장면 모델링을 위한 텐서

본 논문에서는 radiance field를 모델링하고 재구성하는 데 집중한다. 이 경우, 세 차원은 XYZ 축에 대응하며, 장면이 세 축을 따라 동일하게 복잡하게 보일 수 있기 때문에 $R_1 = R_2 = R_3 = R$을 사용한다.

\[\begin{equation} \mathcal{T} = \sum_{r=1}^{R} \textbf{v}_r^X \circ \textbf{M}_r^{YZ} + \textbf{v}_r^Y \circ \textbf{M}_r^{XZ} + \textbf{v}_r^Z \circ \textbf{M}_r^{XY} \end{equation}\]

또한 표기를 간소화하기 위해 세 가지 유형의 성분 텐서를

\[\begin{equation} \mathcal{A}_r^X = \textbf{v}_r^X \circ \textbf{M}_r^{YZ}, \quad \mathcal{A}_r^Y = \textbf{v}_r^Y \circ \textbf{M}_r^{XZ}, \quad \mathcal{A}_r^Z= \textbf{v}_r^Z \circ \textbf{M}_r^{XY} \end{equation}\]

로 표시한다. 그러면 \(\mathcal{T}_{ijk}\)는 다음과 같아진다.

\[\begin{equation} \mathcal{T}_{ijk} = \sum_{r=1}^R \sum_{m \in XYZ} \mathcal{A}_{r, ijk}^m \\ \mathcal{A}_{r, ijk}^X = \textbf{v}_{r,i}^X \textbf{M}_{r,jk}^{YZ}, \quad \mathcal{A}_{r, ijk}^Y = \textbf{v}_{r,j}^Y \textbf{M}_{r,ik}^{XZ}, \quad \mathcal{A}_{r, ijk}^Z = \textbf{v}_{r,k}^Z \textbf{M}_{r,ij}^{XY} \end{equation}\]

Tensorial Radiance Field Representation

(아래에서는 VM decomposition을 사용한 TensoRF만 다루지만, CP decomposition은 더 간단하고 최소한의 수정으로 적용가능하다.)

1. Feature grids and radiance field

본 논문의 목표는 모든 3D 위치 $\textbf{x}$와 뷰 방향 $d$를 volume density $\sigma$와 뷰에 따른 색상 $c$에 매핑하는 함수인 radiance field를 모델링하는 것이다. 이러한 함수를 모델링하기 위해 geometry grid \(\mathcal{G}_\sigma\)와 appearance grid \(\mathcal{G}_c\)로 분할하여 $\sigma$와 $c$를 별도로 모델링한다.

이 접근 방식은 appearance feature 벡터와 뷰 방향 $d$를 색상 $c$로 변환하는 미리 선택된 함수 $S$에 따라 \(\mathcal{G}_c\)에서 다양한 유형의 feature를 지원한다. 예를 들어, $S$는 작은 MLP 또는 spherical harmonics (SH) 함수일 수 있으며, 이 경우 \(\mathcal{G}_c\)는 각각 neural feature와 SH 계수이다. \(\mathcal{G}_\sigma\)는 변환 함수 없이 volume density를 직접 나타낸다.

\[\begin{equation} \sigma, c = \mathcal{G}_\sigma (\textbf{x}), S (\mathcal{G}_c (\textbf{x}), d) \end{equation}\]

\(\mathcal{G}_\sigma (\textbf{x})\)와 \(\mathcal{G}_c (\textbf{x})\)는 위치 $\textbf{x}$에서 trilinear interpolatation된 feature이다.

2. Factorizing radiance fields

\(\mathcal{G}_\sigma \in \mathbb{R}^{I \times J \times K}\)는 3D 텐서이지만 \(\mathcal{G}_c \in \mathbb{R}^{I \times J \times K \times P}\)는 4D 텐서이다. $P$는 appearance feature의 채널 수이다.

\(\mathcal{G}_\sigma\)는 VM decomposition을 통해 다음과 같이 분해된다.

\[\begin{aligned} \mathcal{G}_\sigma &= \sum_{r=1}^{R_\sigma} \textbf{v}_{\sigma,r}^X \circ \textbf{M}_{\sigma,r}^{YZ} + \textbf{v}_{\sigma,r}^Y \circ \textbf{M}_{\sigma,r}^{XZ} + \textbf{v}_{\sigma,r}^Z \circ \textbf{M}_{\sigma,r}^{XY} \\ &= \sum_{r=1}^{R_\sigma} \sum_{m \in XYZ} \mathcal{A}_{\sigma, r}^m \end{aligned}\]

\(\mathcal{G}_c\)에는 feature에 해당하는 추가 차원이 있다. XYZ 차원과 비교할 때 feature 차원은 rank가 ​​낮다. 따라서 feature 차원을 다른 차원과 결합하지 않고 대신 feature 차원에 대해 벡터 \(\textbf{b}_r\)만 사용한다.

\[\begin{aligned} \mathcal{G}_c &= \sum_{r=1}^{R_c} \textbf{v}_{c,r}^X \circ \textbf{M}_{c,r}^{YZ} \circ \textbf{b}_{3r-2} + \textbf{v}_{c,r}^Y \circ \textbf{M}_{c,r}^{XZ} \circ \textbf{b}_{3r-1} + \textbf{v}_{c,r}^Z \circ \textbf{M}_{c,r}^{XY} \circ \textbf{b}_{3r} \\ &= \sum_{r=1}^{R_c} \mathcal{A}_{c,r}^X \circ \textbf{b}_{3r-2} + \mathcal{A}_{c,r}^Y \circ \textbf{b}_{3r-1} + \mathcal{A}_{c,r}^Z \circ \textbf{b}_{3r} \end{aligned}\]

총 성분 수와 일치하도록 \(\textbf{b}_r\)은 $3R_c$개가 있다.

전반적으로, 전체 radiance field를 \(3R_\sigma + 3R_c\)개의 행렬과 \(3R_\sigma + 6R_c\)개의 벡터로 분해한다. 일반적으로 $I, J, K$보다 훨씬 작은 \(R_\sigma\)와 \(R_c\)를 채택하여 고해상도 density grid를 인코딩할 수 있는 매우 컴팩트한 표현을 얻는다. 모든 \(\textbf{b}_r\)을 열로 쌓으면 행렬 \(\textbf{B} \in \mathbb{R}^{P \times 3R_c}\)가 되며, 이 행렬은 전체 장면에서 나타나는 외형의 공통점을 추상화한 글로벌 사전으로 볼 수도 있다.

3. Efficient feature evaluation

직접적인 평가

VM decomposition을 사용하면 인덱스 $ijk$에서 density 값 \(\mathcal{G}_{\sigma, ijk}\)를 직접적이고 효율적으로 평가할 수 있다.

\[\begin{equation} \mathcal{G}_{\sigma, ijk} = \sum_{r=1}^{R_\sigma} \sum_{m \in XYZ} \mathcal{A}_{\sigma,r,ijk}^m \end{equation}\]

각 \(\mathcal{A}_{\sigma,r,ijk}^m\)를 계산하려면 해당 벡터와 행렬에서 두 값을 인덱싱하고 곱하기만 하면 된다.

\(\mathcal{G}_c\)의 경우, 항상 셰이딩 함수 $S$가 입력으로 요구하는 전체 $P$-채널 feature 벡터를 계산해야 하며, 이는 고정된 XYZ 인덱스 $ijk$에서 \(\mathcal{G}_c\)의 1D 슬라이스에 해당한다.

\[\begin{equation} \mathcal{G}_c = \sum_{r=1}^{R_c} \mathcal{A}_{c,r,ijk}^X \textbf{b}_{3r-2} + \mathcal{A}_{c,r,ijk}^Y \textbf{b}_{3r-1} + \mathcal{A}_{c,r,ijk}^Z \textbf{b}_{3r} \end{equation}\]

전체 벡터를 계산하므로 feature 차원에 대한 추가 인덱싱이 없다. 계산을 재정렬하여 위 식을 더욱 단순화할 수 있다.

\[\begin{equation} \mathcal{G}_{c,ijk} = \textbf{B}(\oplus [\mathcal{A}_{c,ijk}^m]_{m,r}) \end{equation}\]

여기서 \(\oplus [\mathcal{A}_{c,ijk}^m]_{m,r}\)은 $m = X, Y, Z$와 $r = 1, \ldots, R_c$에 대한 모든 \(\mathcal{A}_{c,ijk}^m\) 값을 쌓는 $3 R_c$ 차원의 벡터이다. $\oplus$는 실제로 모든 스칼라 값을 $3R_c$ 채널의 벡터로 concatenate하는 concatenation 연산자로 간주할 수도 있다.

많은 수의 voxel을 병렬로 계산할 때, 먼저 행렬의 열 벡터로서 모든 voxel에 대해 \(\mathcal{A}_{c,ijk}^m\)를 계산하고 concatenate한 다음 공유 행렬 $\textbf{B}$를 한 번 곱하기 때문에 위 식은 형식적으로 더 간단할 뿐만 아니라 실제로 구현이 더 간단하다.

Trilinear interpolation

연속적인 radiance field를 모델링하기 위해 trilinear interpolation을 적용한다. 단순하게 trilinear interpolation을 구현하는 것은 비용이 많이 들며, 8개의 텐서 값을 평가하고 보간해야 하며, 하나의 텐서 성분을 계산하는 것보다 8배의 계산이 필요하다. 그러나 텐서를 trilinear interpolation하는 것은 해당 차원에 대해 벡터/행렬을 각각 linear/bilinear로 보간하는 것과 자연스럽게 동일하다.

예를 들어, 각 텐서 성분이 \(\mathcal{A}_{r,ijk}^X = \textbf{v}_{r,i}^X \textbf{M}_{r,ijk}^{YZ}\)인 텐서 \(\mathcal{A}_r^X = \textbf{v}_r^X \circ \textbf{M}_r^{YZ}\)가 주어지면 보간된 값을 다음과 같이 계산할 수 있다.

\[\begin{equation} \mathcal{A}_r^X (\textbf{x}) = \textbf{v}_r^X (x) \textbf{M}_r^{YZ} (y, z) \end{equation}\]

\(\mathcal{A}_r^X (\textbf{x})\)는 3차원 공간에서 trilinear interpolatation된 $\textbf{x} = (x, y, z)$에서의 \(\mathcal{A}_r^X\)의 값이며, \(\textbf{v}_r^X (x)\)는 X축을 따라 $x$에서 linear interpolatation된 $\textbf{v}_r^X$의 값이고, \(\textbf{M}_r^{YZ} (y, z)\)는 YZ 평면에서 bilinear interpolatation된 $(y, z)$에서의 \(\textbf{M}_r^{YZ}\) 값이다.

마찬가지로 \(\mathcal{A}_r^Y (\textbf{x}) = \textbf{v}_r^Y (y) \textbf{M}_r^{XZ} (x,z)\)이고 \(\mathcal{A}_r^Z (\textbf{x}) = \textbf{v}_r^Z (z) \textbf{M}_r^{XY} (x,y)\)이다. 따라서 두 그리드를 trilinear interpolatation하는 것은 다음과 같이 표현된다.

\[\begin{aligned} \mathcal{G}_\sigma (\textbf{x}) &= \sum_r \sum_m \mathcal{A}_{\sigma,r}^m (\textbf{x}) \\ \mathcal{G}_c (\textbf{x}) &= \textbf{B} (\oplus [\mathcal{A}_{c,r}^m (\textbf{x})]_{m,r}) \end{aligned}\]

Trilinear interpolatation을 위해 8개의 개별 텐서 성분을 복구하는 것을 피하고 대신 보간된 값을 직접 복구하여 런타임 시 계산 및 메모리 비용이 낮아진다.

4. Rendering and reconstruction

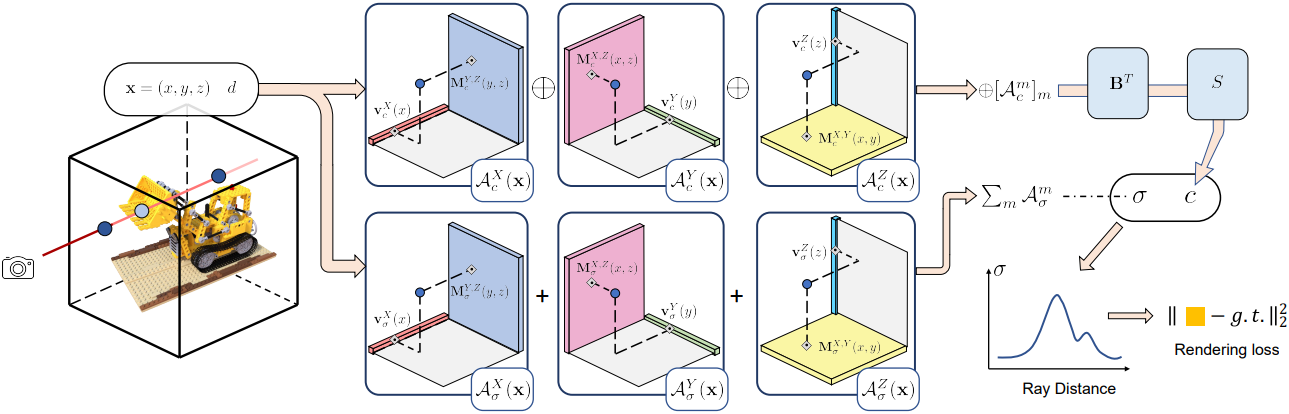
위의 식들을 결합하면 radiance field는 다음과 같이 표현될 수 있다.

\[\begin{aligned} \sigma &= \sum_r \sum_m \mathcal{A}_{\sigma,r}^m (\textbf{x}) \\ c &= S (\textbf{B} (\oplus [\mathcal{A}_{c,r}^m (\textbf{x})]_{m,r}), d) \end{aligned}\]

얻은 $\sigma$와 $c$를 사용하여 고품질의 재구성 및 렌더링이 가능하다.

Volume rendering

이미지를 렌더링하기 위해 NeRF를 따라 미분 가능한 볼륨 렌더링을 사용한다. 구체적으로, 각 픽셀에 대해 광선을 따라 이동하면서 광선을 따라 $Q$개의 shading point들을 샘플링하고 픽셀 색상을 계산한다.

\[\begin{equation} C = \sum_{q=1}^Q \tau_q (1 - \exp (-\sigma_q \Delta_q)) c_q, \quad \tau_q = \exp (- \sum_{p=1}^{q-1} \sigma_p \Delta_p) \end{equation}\]

$\sigma_q$와 $c_q$는 \(\textbf{x}_q\)에서 계산된 volume density와 색상이며, $\Delta_q$는 ray step size이다.

Reconstruction

알려진 카메라 포즈가 있는 멀티뷰 입력 이미지 세트가 주어지면, gradient descent를 통해 장면별로 최적화되어 L2 렌더링 loss를 최소화하고, GT 픽셀 색상만을 supervision으로 사용한다. Radiance field는 텐서 분해로 설명되고, 글로벌 벡터와 행렬 세트로 모델링된다. 그러나 이것은 때때로 overfitting과 local minima 문제를 야기하여 관측 정보가 적은 영역에서 outlier나 noise를 유발할 수 있다.

저자들은 벡터와 행렬에 대한 정규화 loss \(\mathcal{L}_\textrm{reg}\)로 L1 norm loss \(\mathcal{L}_\textrm{L1}\) 또는 TV (total variation) loss \(\mathcal{L}_\textrm{TV}\)를 사용하여 이러한 문제를 효과적으로 해결하였다. L1 norm loss만 적용하여도 대부분의 데이터셋에 적합하지만, 입력 이미지가 매우 적은 실제 데이터셋 (ex. LLFF) 또는 캡처 조건이 불완전한 실제 데이터셋 (ex. 노출이 다양하고 마스크가 일관되지 않은 Tanks and Temples)의 경우 TV loss가 L1 norm loss보다 효율적이다.

\[\begin{aligned} \mathcal{L} &= \| C - C_\textrm{GT} \|_2^2 + \omega \cdot \mathcal{L}_\textrm{reg} \\ \mathcal{L}_\textrm{L1} &= \frac{1}{N} \sum_{r=1}^{R_\sigma} (\| \textbf{M}_{\sigma, r} \| + \| \textbf{v}_{\sigma, r} \|) \\ \mathcal{L}_\textrm{TV} &= \frac{1}{N} \sum ( \sqrt{\Delta^2 \mathcal{A}_{\sigma, r}^m} + 0.1 \cdot \sqrt{\Delta^2 \mathcal{A}_{c,r}^m} ) \end{aligned}\]

$\Delta^2$는 이웃 값 사이의 차이의 제곱이며, $N$은 파라미터의 총 개수이다. 정규화 항으로 \(\mathcal{L}_\textrm{L1}\)을 사용하면 $\omega = 0.0004$이고, \(\mathcal{L}_\textrm{TV}\)를 사용하면 $\omega = 1$이다.

추가로, 품질을 더욱 개선하고 local minima를 피하기 위해 coarse-to-fine reconstruction을 적용하였으며, 단순히 XYZ 벡터와 행렬 성분을 linear 및 bilinear interpolatation으로 업샘플링하여 적용할 수 있다.

Experiments

• 구현 디테일
  • $P$ = 27
    • SH의 경우 RGB 3개 $\times$ 3rd-order SH 계수 9개
    • MLP의 경우 2-layer FC + ReLU를 사용 (hidden layer는 128차원)
  • optimizer: Adam
  • 초기 learning rate
    • 텐서의 벡터와 행렬: 0.02
    • MLP: 0.001
  • batch size: 4096 pixel ray
  • coarse-to-fine reconstruction
    • 초기 그리드 해상도: $128^3$
    • 2000, 3000, 4000, 5500, 7000 iteration에서 업샘플링
    • 그리드 해상도는 최종 그리드 해상도까지 로그로 증가
  • 최종 그리드 해상도, 전체 iteration, $R_\sigma$, $R_c$는 장면마다 다름
  • GPU: Tesla V100 GPU (16GB) 1개

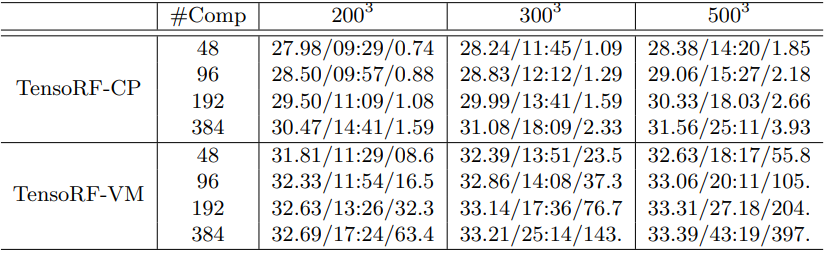
다음은 Synthetic-NeRF에서 다양한 TensorRF 모델을 분석한 표이다. (평균 PSNR / 최적화 시간 (분:초) / 모델 크기 (MB))

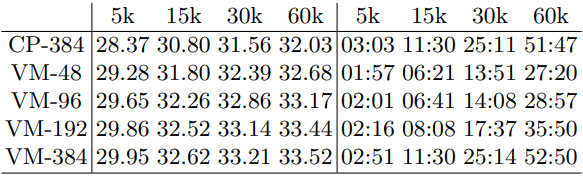
다음은 Synthetic-NeRF에서 학습 iteration에 따른 PSNR과 최적화 시간을 비교한 표이다.

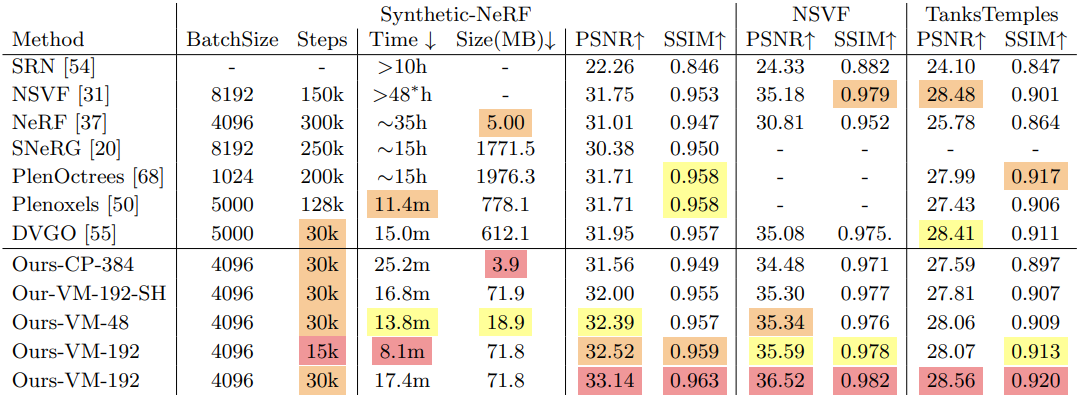
다음은 기존 방법들과 세 가지 데이터셋에서 비교한 표이다.

다음은 Synthetic-NeRF에서의 재구성 결과를 정성적으로 비교한 것이다.

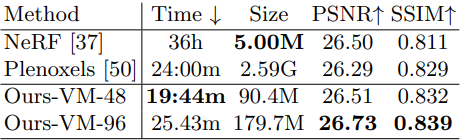
다음은 앞을 향한 장면에 대한 재구성 결과를 비교한 표이다.

Limitations

경계가 있는 장면만 지원하고 전경과 배경 콘텐츠가 모두 있는 경계가 없는 장면을 처리할 수 없다.