[논문리뷰] Bridging the Skeleton-Text Modality Gap: Diffusion-Powered Modality Alignment for Zero-shot Skeleton-based Action Recognition

ICCV 2025. [Paper] [Page] [Github]
Jeonghyeok Do, Munchurl Kim
KAIST
16 Nov 2024

Introduction

Fully supervised learning 방식의 스켈레톤 기반 동작 인식 방법은 일반적으로 우수한 성능을 보이지만, 수많은 동작 클래스에 대해 모두 주석을 다는 것은 현실적으로 불가능하다. 또한, 새로운 클래스에 대한 모델 재학습에는 상당한 비용이 소요된다. 따라서 zero-shot skeleton-based action recognition (ZSAR)은 명시적인 학습 데이터 없이도 미지의 동작에 대한 예측을 가능하게 함으로써 이러한 문제를 해결한다.

중요한 것은 인간의 동작들이 관련 동작들 간에 공통적인 스켈레톤 움직임 패턴을 공유하는 경우가 많다는 점이다. ZSAR 방법은 이러한 공유 패턴을 활용하여 사전 학습된 스켈레톤 feature를 텍스트 기반 동작 설명과 정렬함으로써, 모델이 관찰된 동작에서 미지의 동작으로 extrapolation할 수 있도록 한다. 이러한 정렬 기반 접근 방식은 모델의 판별력을 강화하여 실제 시나리오에서 확장성과 신뢰성 있는 zero-shot 인식을 보장한다.

그러나 스켈레톤 feature와 텍스트 feature 간의 효과적인 정렬을 달성하는 것은 상당한 어려움을 수반한다. 스켈레톤 데이터는 시간적, 공간적 움직임 패턴을 포착하는 반면, 동작 레이블에 대한 텍스트 설명은 고차원적인 semantic 정보를 담고 있다. 이러한 모달리티 차이로 인해 두 latent space를 효과적으로 정렬하기 어렵고, 결과적으로 학습되지 않은 동작에 대한 일반화 학습이 저해된다.

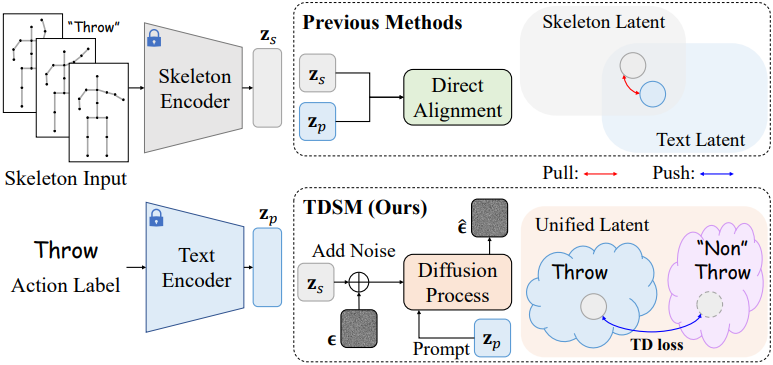
Diffusion model의 컨디셔닝 메커니즘은 정확한 cross-modal 정렬을 가능하게 하여 생성된 출력이 주어진 조건에 충실하게 부합하도록 한다. 이러한 특성에 착안하여, 본 논문에서는 diffusion model을 ZSAR에 적용하고 텍스트 프롬프트를 기반으로 denoising process를 컨디셔닝하는 새로운 프레임워크인 Triplet Diffusion for Skeleton-Prompt Matching (TDSM)을 제안하였다. 본 접근 방식은 reverse process를 활용하여 공유된 latent space 내에서 스켈레톤 feature와 텍스트 feature를 암시적으로 정렬함으로써, 직접적인 feature space 정렬의 어려움을 극복한다.

구체적으로, TDSM은 텍스트 프롬프트를 조건으로 하여 noise가 더해진 스켈레톤 feature의 noise를 제거하고, 프롬프트를 통합된 스켈레톤-텍스트 latent space에 임베딩하여 동작 레이블의 semantic을 더욱 효과적으로 포착한다. 이러한 암시적 정렬은 직접적인 latent space 매핑의 한계를 완화하고 robustness를 향상시킨다.

또한, 본 논문에서는 triplet diffusion (TD) loss를 도입하여, 올바른 스켈레톤-텍스트 쌍에 대해서는 더욱 긴밀한 정렬을 유도하고, 잘못된 쌍에 대해서는 정렬을 약화시킴으로써 모델의 판별력을 더욱 향상시킨다. 추가적인 이점으로, 학습 중에 추가되는 랜덤 noise로 인해 발생하는 diffusion process의 확률적 특성은 자연스러운 정규화 메커니즘 역할을 한다. 이는 overfitting을 방지하고 모델이 이전에 보지 못한 동작에 대해 효과적으로 일반화하는 능력을 향상시킨다.

Method

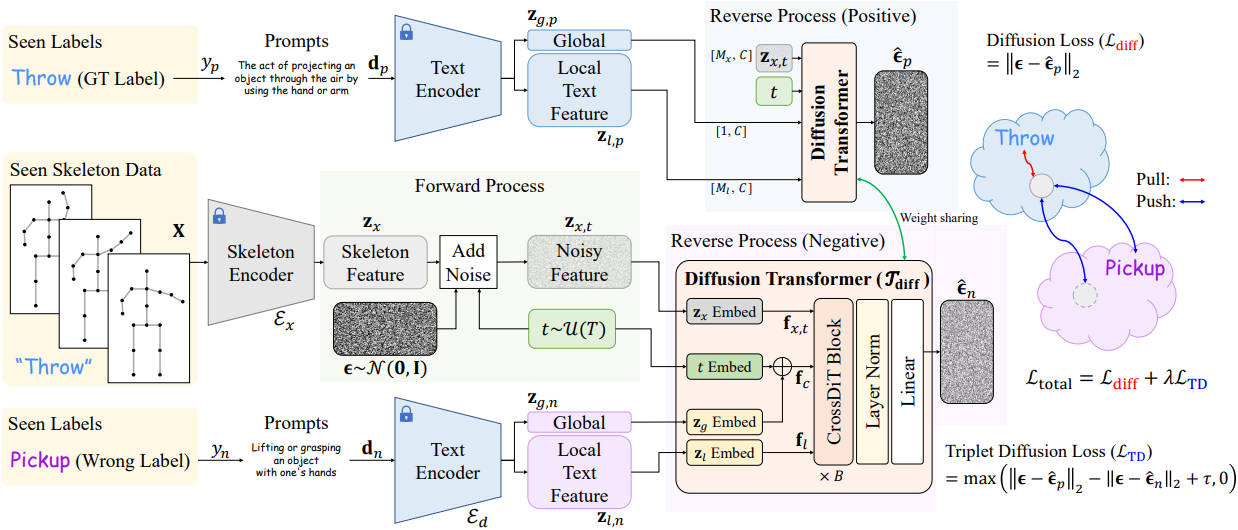
데이터셋은 다음과 같이 주어진다.

\[\begin{equation} \mathcal{D}_\textrm{train} = \{(\textbf{X}_i, y_i)\}_{i=1}^N, \; \mathcal{D}_\textrm{train} = \{(\textbf{X}_j^u, y_j^u)\}_{j=1}^{N_u} \\ y_i \in \mathcal{Y}, \; y_j^u \in \mathcal{Y}_u, \; \mathcal{Y} \cap \mathcal{Y}_u = \varnothing \end{equation}\]

\(\textbf{X}_i, \textbf{X}_j^u \in \mathbb{R}^{T \times V \times M \times C_\textrm{in}}\)은 스켈레톤 시퀀스이며, 시퀀스 길이가 $T$, joint의 수가 $V$, actor의 수가 $M$, 각 joint 차원이 \(C_\textrm{in}\)이다.

1. Embedding Skeleton and Prompt Input

사전 학습된 스켈레톤 인코더 \(\mathcal{E}_x\)와 텍스트 인코더 \(\mathcal{E}_d\)는 스켈레톤 입력 $\textbf{X}$와 프롬프트 입력 $\textbf{d}$를 동작 레이블 $\textbf{y}$와 함께 각각의 feature space에 임베딩하여 스켈레톤 feature \(\textbf{z}_x\)와 글로벌 텍스트 feature \(\textbf{z}_g\) 및 로컬 텍스트 feature \(\textbf{z}_l\)을 생성한다.

스켈레톤 인코더 \(\mathcal{E}_x\)의 경우, 아키텍처로 Graph Convolutional Network (GCN)을 채택하고, 이를 학습 데이터셋 \(\mathcal{D}_\textrm{train}\) 사용하여 cross-entropy loss로 학습시킨다.

\[\begin{equation} \mathcal{L}_\textrm{CE} = -\sum_{k=1}^{\vert \mathcal{Y} \vert} \textbf{y}(k) \log \hat{\textbf{y}}(k), \quad \textrm{where} \; \hat{\textbf{y}} = \textrm{MLP} (\mathcal{E}_x (\textbf{X})) \end{equation}\]

학습이 완료되면 스켈레톤 인코더 \(\mathcal{E}_x\)의 파라미터가 고정되어 스켈레톤 latent 표현 \(\textbf{z}_x = \mathcal{E}_x (\textbf{X})\)를 생성하는 데 사용된다. Attention layer를 위해 feature를 reshape하면 \(\textbf{z}_x\)는 $\mathbb{R}^{M_x \times C}$이 된다.

텍스트 인코더 \(\mathcal{E}_d\)의 경우, 텍스트 프롬프트를 활용하여 동작 레이블에 대한 풍부한 semantic 정보를 추출한다. 각 GT 레이블 \(\textbf{y}_p = y\)는 프롬프트 \(\textbf{d}_p\)이 할당되고, 무작위로 선택된 오답 레이블 \(\textbf{y}_n \in \mathcal{Y} \backslash \{\textbf{y}_p\}\)에는 프롬프트 \(\textbf{d}_n\)이 할당된다. 프롬프트를 인코딩하기 위해 CLIP과 같은 사전 학습된 텍스트 인코더를 사용하며, 글로벌 텍스트 feature \(\textbf{z}_g \in \mathbb{R}^{1 \times C}\)와 로컬 텍스트 feature \(\textbf{z}_l \in \mathbb{R}^{M_l \times C}\)의 두 가지 유형의 feature를 사용한다. 주어진 프롬프트 $\textbf{d}$에 대한 텍스트 인코더의 출력은 다음과 같이 표현할 수 있다.

\[\begin{equation} [\textbf{z}_g \; \vert \; \textbf{z}_l] = \mathcal{E}_d (\textbf{d}) \end{equation}\]

($[\cdot \vert \cdot]$은 token-wise concat)

\(\textbf{d}_p\)와 \(\textbf{d}_n\)에 대해 각각 \(\textbf{z}_{g,p}\), \(\textbf{z}_{l,p}\)와 \(\textbf{z}_{g,n}\), \(\textbf{z}_{l,n}\)이 추출되며, 이 4개의 feature는 diffusion process를 컨디셔닝하는 데 사용된다.

2. Diffusion Process

본 프레임워크는 denoising process를 활용하여 데이터를 생성하는 것이 아니라, reverse process를 통해 스켈레톤 feature과 텍스트 프롬프트를 융합하여 판별력이 뛰어난 스켈레톤 latent space를 학습한다. TDSM은 스켈레톤 feature의 noise를 제거하여 결과적으로 생성되는 latent space가 동작 레이블에 대해 판별력을 갖도록 학습된다.

Forward process

총 $T$ timestep 내에서 샘플링한 랜덤 timestep $t \sim \mathcal{U}(T)$에 대하여 랜덤 Gaussian noise가 추가된다.

\[\begin{equation} \textbf{z}_{x,t} = \sqrt{\vphantom{1} \bar{\alpha}_t} \textbf{z}_x + \sqrt{1 - \bar{\alpha}_t} \epsilon \end{equation}\]

Reverse process

DiT \(\mathcal{T}_\textrm{diff}\)는 주어진 timestep $t$에서의 글로벌 텍스트 feature \(\textbf{z}_g\)와 로컬 텍스트 feature \(\textbf{z}_l\)을 조건으로 하여 noise가 포함된 \(\textbf{z}_{x,t}\)로부터 noise \(\hat{\epsilon}\)을 예측한다.

\[\begin{equation} \hat{\epsilon} = \mathcal{T}_\textrm{diff} (\textbf{z}_{x,t}, t; \textbf{z}_g, \textbf{z}_l) \end{equation}\]

GT 레이블에 대하여 \(\hat{\epsilon}_p\)를, 오답 레이블에 대하여 \(\hat{\epsilon}_n\)를 예측한다. 저자들은 상대적으로 작은 규모의 스켈레톤 데이터를 수용하기 위해 block/채널 수를 줄이고, 스켈레톤-텍스트 정렬을 향상시키기 위해 글로벌 및 로컬 텍스트 임베딩을 모두 통합하였다.

Triplet diffusion (TD) loss

전체 학습 loss는 diffusion loss와 기존의 triplet loss에서 영감을 받아 재구성한 TD loss를 결합한 것이다.

\[\begin{equation} \mathcal{L}_\textrm{total} = \mathcal{L}_\textrm{diff} + \lambda \mathcal{L}_\textrm{TD} \end{equation}\]

Diffusion loss \(\mathcal{L}_\textrm{diff}\)는 정확한 denoising을 보장하고, TD loss \(\mathcal{L}_\textrm{TD}\)는 올바른 레이블 예측과 잘못된 레이블 예측을 구별하는 능력을 향상시킨다.\(\mathcal{L}_\textrm{diff}\)와 \(\mathcal{L}_\textrm{TD}\)는 다음과 같다.

\[\begin{aligned} \mathcal{L}_\textrm{diff} &= \| \hat{\epsilon} - \epsilon_p \|_2 \\ \mathcal{L}_\textrm{TD} &= \max(\| \epsilon - \hat{\epsilon}_p \|_2 - \| \epsilon - \hat{\epsilon}_n \|_2 + \tau, 0) \end{aligned}\]

($\epsilon$은 실제 noise, \(\hat{epsilon}_p\)는 GT 텍스트 feature에 대한 예측 noise, \(\hat{\epsilon}_n\)은 잘못된 텍스트 feature에 대한 예측 noise, $\tau$는 margin 파라미터)

\(\mathcal{L}_\textrm{TD}\)는 간단하지만 매우 효과적이며, $\epsilon$과 \(\hat{epsilon}_p\) 사이의 거리를 최소화하는 동시에 \(\hat{\epsilon}_n\)에 대한 거리를 최대화하도록 유도하여 학습된 스켈레톤-텍스트 latent space에서 두 가지 모달리티의 판별적인 융합을 보장한다.

3. Inference Phase

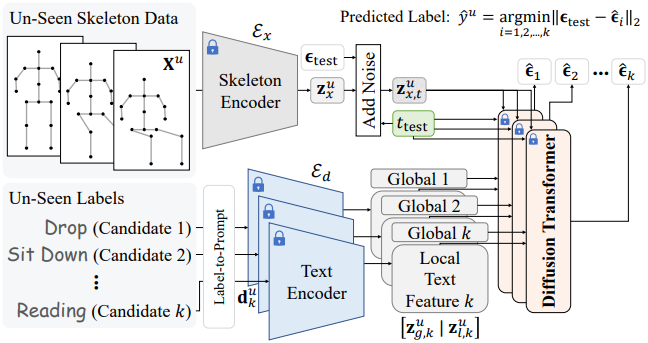
Inference 시에는 각 미지의 스켈레톤 시퀀스 \(\textbf{X}_u\)와 모든 후보 텍스트 프롬프트가 TDSM에 입력되고, 모든 후보 텍스트 프롬프트에 대한 결과 noise는 고정된 GT noise \(\epsilon_\textrm{test} \sim \mathcal{N}(0,I)\)와 비교된다. \(\textbf{X}_u\)는 먼저 \(\mathcal{E}_x\)를 통해 다음과 같이 스켈레톤 latent space로 인코딩된다.

\[\begin{equation} \textbf{z}_x^u = \mathcal{E}_x (\textbf{X}^u) \end{equation}\]

각 후보 동작 레이블 \(y_k^u \in \mathcal{Y}_u\)는 프롬프트 \(\textbf{d}_k^u\)와 연결되며, \(\textbf{d}_k^u\)는 \(\mathcal{E}_d\)를 통해 처리되어 글로벌 및 로컬 텍스트 feature가 추출된다.

\[\begin{equation} [\textbf{z}_{g,k}^u \; \vert \; \textbf{z}_{l,k}^u] = \mathcal{E}_d (\textbf{d}_k^u) \end{equation}\]

다음으로, 고정된 Gaussian noise \(\epsilon_\textrm{test}\)와 고정된 timestep \(t_\textrm{test}\)로 forward process를 수행하여 noise가 포함된 스켈레톤 feature을 생성한다.

\[\begin{equation} \textbf{z}_{x,t}^u = \sqrt{\vphantom{1} \bar{\alpha}_{t_\textrm{test}}} \textbf{z}_x^u + \sqrt{1 - \bar{\alpha}_{t_\textrm{test}}} \epsilon_\textrm{test} \end{equation}\]

$y_k^u$에 대하여, \(\mathcal{T}_\textrm{diff}\)는 noise \(\hat{\epsilon}_k\)를 예측한다.

\[\begin{equation} \hat{\epsilon}_k = \mathcal{T}_\textrm{diff} (\textbf{z}_{x,t}^u, t_\textrm{test}; \textbf{z}_{g,k}^u, \textbf{z}_{l,k}^u) \end{equation}\]

$y_k^u$에 대한 점수는 \(\epsilon_\textrm{test}\)와 \(\hat{\epsilon}_k\) 사이의 \(\ell_2\)-norm으로 계산된다. 예측 레이블 \(\hat{y}^u\)는 이 거리를 최소화하는 레이블이다.

\[\begin{equation} \hat{y}^u = \underset{k}{\arg \min} \| \epsilon_\textrm{test} - \hat{\epsilon}_k \|_2 \end{equation}\]

이 과정을 통해 모델은 텍스트 프롬프트가 스켈레톤 시퀀스와 잘 일치하는 동작 레이블을 선택하게 되므로, 이전에 보지 못한 동작 레이블이 있는 스켈레톤 시퀀스에 대해서도 정확한 zero-shot 인식이 가능하다. 샘플을 반복적으로 개선하는 생성 모델과 달리, 본 논문에서 제시하는 TDSM은 고정된 timestep으로 한 번의 inference를 수행하므로 효율적이며 판별적인 스켈레톤-텍스트 정렬에 매우 적합하다.

Experiments

• 구현 디테일
  • GPU: NVIDIA GeForce RTX 3090 1개
  • iteration: 50,000
  • optimizer: AdamW
    • learning rate: $1 \times 10^{-4}
    • weight decay: 0.01
    • warm-up: 100 step
    • cosine-annealing scheduler
  • batch size: 256
  • $\lambda = 1.0$, $\tau = 1.0$
  • timestep: $T = 50$, \(t_\textrm{test} = 25\)

1. Performance Evaluation

다음은 SynSE와 PURLS 벤치마크에 대한 비교 결과이다.

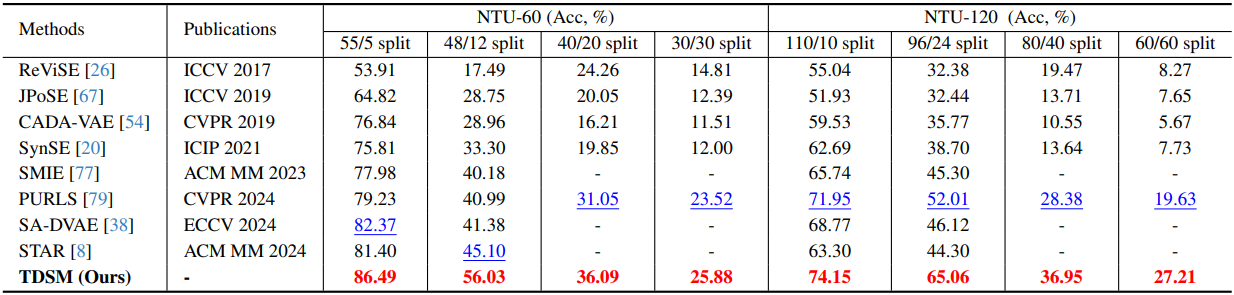
다음은 SMIE 벤치마크에 대한 비교 결과이다.

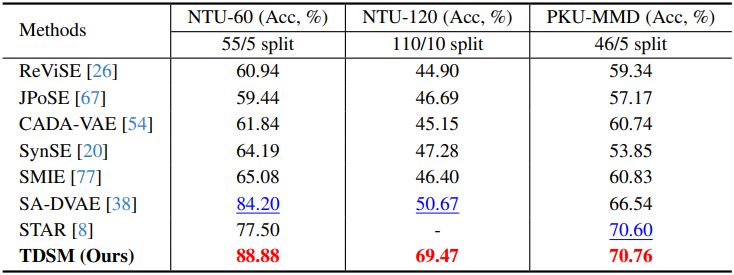
2. Ablation Studies

다음은 loss function에 대한 ablation study 결과이다.

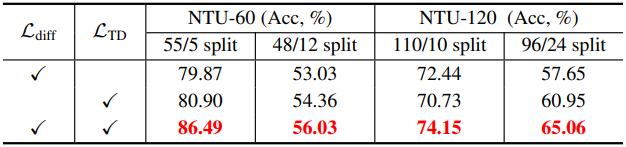
다음은 텍스트 feature 유형에 대한 ablation study 결과이다.

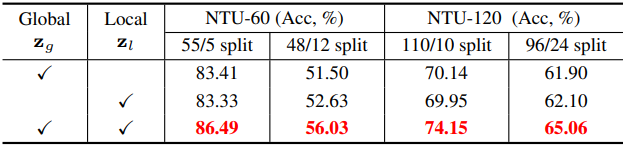
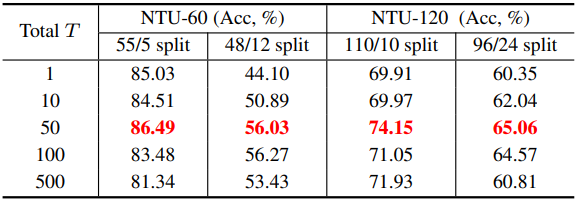
다음은 총 timestep 수 $T$에 대한 ablation study 결과이다.

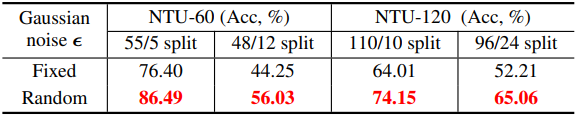
다음은 학습 중에 사용한 Gaussian noise $\epsilon$에 대한 ablation study 결과이다.

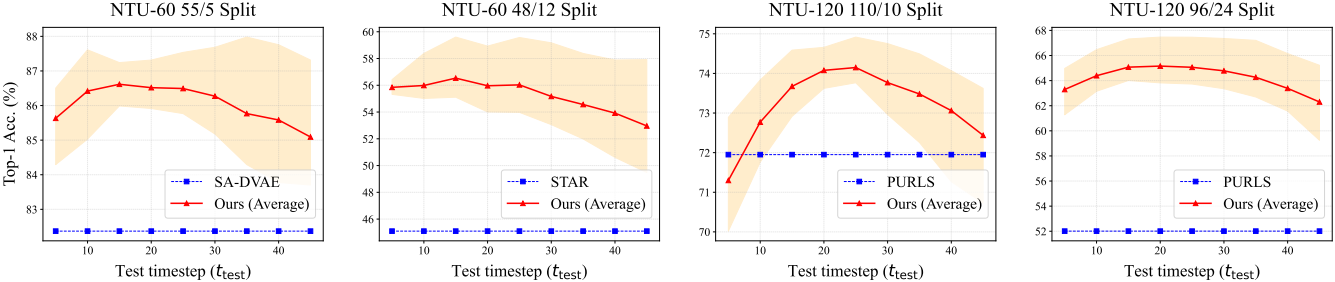
다음은 \(t_\textrm{test}\)에 대한 ablation study 결과이다.