[논문리뷰] Truncated Consistency Models

ICLR 2025. [Paper] [Page] [Github]
Sangyun Lee, Yilun Xu, Tomas Geffner, Giulia Fanti, Karsten Kreis, Arash Vahdat, Weili Nie
Carnegie Mellon University | NVIDIA
18 Oct 2024

Introduction

Consistency model은 diffusion model의 생성 속도를 높이기 위해 one-step으로 초기 noise로부터 PF ODE의 해를 직접 예측하는 방법을 학습한다. 많은 수의 noise-데이터 쌍을 시뮬레이션할 필요성을 피하기 위해 consistency model은 ODE 궤적을 따라 두 인접 지점에서 모델 출력 간의 불일치를 최소화하는 방법을 학습한다. $t = 0$의 경계 조건은 앵커 역할을 하여 이러한 출력을 실제 데이터에 연결한다. 시뮬레이션 없는 학습을 통해 모델은 서로 다른 시간에 대한 매핑을 점진적으로 개선하여 경계 조건을 $t = 0$에서 초기 $t = T$로 전파한다.

그러나 시뮬레이션 없는 학습의 장점은 trade-off들을 수반한다. Consistency model은 위 그림의 (a)에서 볼 수 있듯이, PF ODE 궤적 위의 모든 지점을 해당 데이터 종점에 매핑하는 방법을 학습해야 한다. 이를 위해서는 데이터가 부분적으로만 손상되는 PF ODE에서 더 짧은 시간 동안의 denoising과, 대부분의 원본 데이터 정보가 삭제되는 $t = T$ 시점으로의 생성을 모두 학습해야 한다. 이러한 이중 task는 더 큰 네트워크 용량을 필요로 하며, 하나의 모델이 두 task 모두에서 뛰어난 성과를 내는 것은 어렵다. 경험적으로 모델은 학습이 진행됨에 따라 생성 품질을 위해 작은 $t$에 대한 denoising 성능을 점진적으로 희생한다. 최종 목표가 denoising이 아닌 생성이기 때문에 이러한 행동은 바람직하지만, 저자들은 모델이 시간에 따라 네트워크 용량을 제어할 수 없게 할당하는 대신 이러한 trade-off를 명시적으로 제어할 것을 주장하였다.

생성 성능을 향상시키기 위해 denoising task에 할당된 네트워크 용량을 명시적으로 줄일 수 있을까?

본 논문에서는 작은 $t$에서 denoising을 덜 강조하면서도 큰 $t$에 대한 consistency mapping을 보존하기 위해 Truncated Consistency Models (TCM)이라는 새로운 학습 알고리즘을 제안하였다. TCM은 PF ODE 궤적의 전체 시간 범위 $[0, T]$에 걸쳐 학습을 요구하는 기존의 consistency objective를 완화하여, $[t^\prime, T]$라는 잘린 시간 범위에 초점을 맞춘 새로운 objective로 전환한다. 여기서 $t^\prime$은 denoising task와 생성 task를 구분하는 분기 시점으로 작용한다. 이를 통해 모델은 용량을 주로 생성에 전념하여 더 이른 시간 $[0, t^\prime)$에서 denoising task에서 벗어날 수 있다.

새로운 모델이 원래의 일관성 매핑을 고수하도록 하려면 $t^\prime$에서 적절한 경계 조건이 필요하다. 이를 위해 저자들은 2단계 학습 절차를 제안하였다. 첫 번째 단계는 전체 시간 범위에 걸쳐 표준 consistency model을 사전 학습시킨다. 이렇게 사전 학습된 모델은 TCM의 후속적인 truncated consistency training 단계에 대한 $t^\prime$의 경계 조건으로 작용한다.

TCM은 다양한 데이터셋과 샘플링 step 수에서 consistency model의 샘플 품질과 학습 안정성을 모두 향상시킨다. 비슷한 크기의 가장 우수한 consistency model인 iCT보다 성능이 뛰어나며, 네트워크 크기가 2배 큰 iCT-deep 보다도 성능이 뛰어나다. TCM은 ImageNet 64$\times$64에서 one-step FID의 SOTA를 달성하였으며, 표준 consistency training에서 관찰되는 발산은 TCM에서는 나타나지 않는다.

Consistency Model

Consistency model은 $t \in [0,T]$에서 시작하여 PF ODE의 해를 출력하는 consistency function을 학습함으로써 noise에서 데이터로 직접 매핑하는 것을 목표로 한다. Consistency function $\textbf{f}$는 다음 두 가지 속성을 만족해야 한다.

\[\begin{aligned} & \textbf{f}(\textbf{x}_0, 0) = \textbf{x}_0 \\ & \textbf{f}(\textbf{x}_t, t) = \textbf{f}(\textbf{x}_s, s), \quad \forall (s, t) \in [0, T]^2 \end{aligned}\]

첫 번째 조건은 reparameterization을 통해 충족될 수 있다.

\[\begin{equation} \textbf{f}_\theta (\textbf{x}, t) := c_\textrm{out} (t) \textbf{F}_\theta (\textbf{x}, t) + c_\textrm{skip} \textbf{x} \end{equation}\]

\(\textbf{f}_\theta\)를 직접 학습시키는 대신, 위의 reparameterization 하에 신경망 \(\textbf{F}_\theta\)를 학습시킨다.

두 번째 조건은 다음과 같은 consistency training objective를 최적화하여 학습시킬 수 있다.

\[\begin{equation} \mathcal{L}_\textrm{CT} (\textbf{f}_\theta, \textbf{f}_{\theta^{-}}) := \mathbb{E}_{t \sim \psi_t, \textbf{x} \sim p_\textrm{data}, \boldsymbol{\epsilon} \sim \mathcal{N}(0,\textbf{I})} [\frac{\omega (t)}{\Delta_t} d (\textbf{f}_\theta (\textbf{x} + t \boldsymbol{\epsilon}, t), \textbf{f}_{\theta^{-}} (\textbf{x} + (t - \Delta_t) \boldsymbol{\epsilon}, t - \Delta_t)) ] \\ \textrm{where} \quad \theta^{-} = \textrm{stopgrad}(\theta) \end{equation}\]

(\(\psi_t\)는 시간 샘플링 분포, $\omega(t)$는 weighting function, $d(\cdot, \cdot)$는 distance function)

$\theta$에 대한 \(\mathcal{L}_\textrm{CT}\)의 기울기는 \(\mathcal{O}(\max_t \Delta_t)\) 오차를 갖는 consistency distillation loss의 근사치이다. \(\Delta_t\)는 학습 초기에는 커야 하며, 이는 편향된 기울기를 발생시키지만 안정적인 학습을 가능하게 하고, 후반 단계에서는 어닐링되어야 하며, 이는 오차 항을 감소시키지만 분산을 증가시킨다.

Truncated Consistency Model

표준 consistency model은 다른 많은 생성 모델보다 학습 과정에서 더 큰 어려움을 겪는다. 단순히 noise를 데이터에 매핑하는 대신, consistency model은 PF ODE 궤적의 어느 지점에서든 데이터 종점까지의 매핑을 학습해야 한다. 따라서 consistency model은 denoising task와 생성 task로 네트워크 용량을 분배해야 한다. 이러한 어려움은 네트워크 용량이 유사한 다른 생성 모델에 비해 consistency mdoel의 성능이 떨어지는 주요 원인이다.

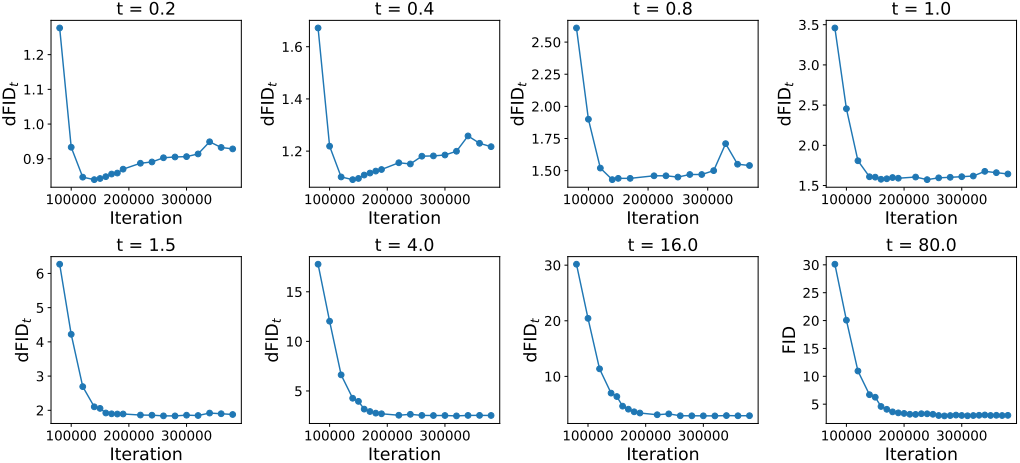
표준 consistency model은 denoising task와 생성 task 간의 trade-off를 암시적으로 탐색한다. 표준 consistency training 과정에서 모델은 낮은 $t$에서 점차 denoising 성능을 잃는다. 구체적으로, 몇 번의 학습 iteration 후 낮은 $t$에서는 denoising FID가 증가하는 반면, 높은 $t$에서는 denoising FID가 계속 감소하는 trade-off를 보여준다. 이는 모델이 denoising과 생성을 동시에 학습하는 데 어려움을 겪고 있으며, 하나를 위해 다른 하나를 희생하고 있음을 시사한다.

Truncated consistency model (TCM)은 consistency training 과정에서 $t$ 값이 작을 때 denoising task를 무시하도록 강제함으로써 이러한 trade-off를 명시적으로 제어하고, 이를 통해 생성 시 네트워크 사용량을 개선하는 것을 목표로 한다. 따라서 consistency model objective를 일반화하고, $t^\prime \in (0, T)$인 절단된 시간 범위 $[t^\prime, T]$에만 적용한다.

단순한 해결책

간단한 접근 방식은 잘린 시간 범위에서 consistency model을 직접 학습시키는 것이다. 그러나 상수 함수 \(\textbf{f}_\theta (x, t) = \textrm{const}\)가 consistency training objective를 최소화하기 때문에 모델 출력은 임의의 상수로 붕괴될 수 있다. 표준 consistency model에서 경계 조건 \(\textbf{f}(\textbf{x}_0, 0) = \textbf{x}_0\)는 붕괴를 방지하지만 이 단순한 해결책에서는 그러한 의미 있는 경계 조건이 없다.

저자들은 이를 해결하기 위해 2단계 학습 절차를 제안하고 적절한 경계 조건을 사용하여 새로운 parameterization을 설계하였다.

제안된 해결책

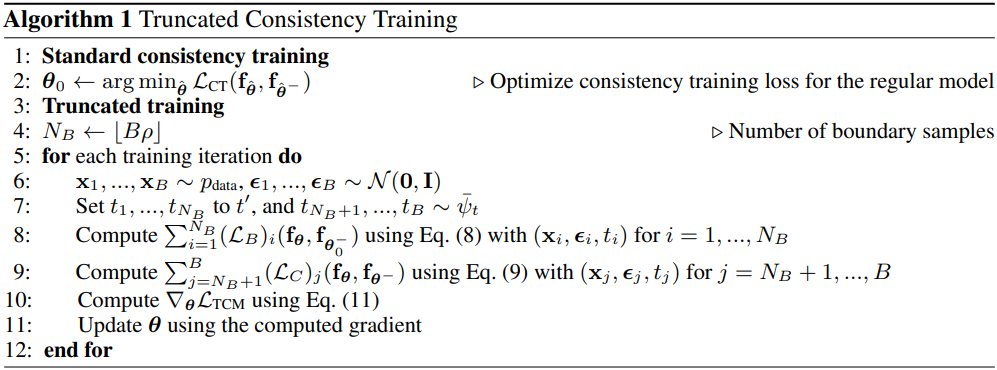
TCM은 두 단계로 학습을 수행한다.

1. 1단계 (Standard consistency training): 표준 consistency training objective를 가지고 일반적인 방식으로 consistency model \(\textbf{f}_{\theta_0}\)을 사전 학습시킨다.
2. 2단계 (Truncated consistency training): 사전 학습된 가중치 \(\textbf{f}_{\theta_0}\)를 사용하여 새로운 consistency model \(\textbf{f}_\theta\)를 초기화하고, 절단된 시간 범위 $[t^\prime, T]$에 대해 학습시킨다. 시간 $t^\prime$에서의 경계 조건은 사전 학습된 \(\textbf{f}_{\theta_0}\)에 의해 제공된다.

먼저 다음과 같은 parameterization을 도입한다.

\[\begin{equation} \textbf{f}_{\theta, \theta_0^{-}}^\textrm{trunc} (\textbf{x}, t) = \textbf{f}_\theta (\textbf{x}, t) \cdot \unicode{x1D7D9} \{t \ge t^\prime\} + \textbf{f}_{\theta_0^{-}} (\textbf{x}, t) \cdot \unicode{x1D7D9} \{t < t^\prime\} \\ \textrm{where} \quad \theta_0^{-} = \textrm{stopgrad}(\theta_0) \end{equation}\]

직관적으로, $t \ge t^\prime$일 때만 최종 모델 \(\textbf{f}_\theta\)를 사용하고, $t < t^\prime$인 경우에는 사전 학습된 \(\textbf{f}_{\theta_0^{-}}\)를 조회한다. 이 접근법은 \(\textbf{f}_\theta\)가 $[0, t^\prime)$에서 네트워크 용량을 낭비하지 않도록 보장하며, \(\textbf{f}_\theta\)가 잘 학습되면 경계에서 사전 학습된 모델 \(\textbf{f}_{\theta_0^{-}}\)을 모방하여 데이터를 생성하는 방법을 학습한다. 샘플링 과정에서 모든 $t \in [t^\prime. T]$에 대해 \(\textbf{f}_{\theta, \theta_0^{-}}^\textrm{trunc} = \textbf{f}_\theta\)이므로, 이 parameterization을 무시하고 \(\textbf{f}_\theta\)만 사용하여 샘플을 생성할 수 있다.

경계 조건을 설명하기 위해, $[t^\prime, T]$를 2개의 범위로 분할한다.

1. 경계 시간 영역 \(S_{t^\prime} = \{t \in \mathbb{R} \, : \, t^\prime \le t \le t^\prime + \Delta_t\}\)
2. Consistency training 시간 영역 \(S_{t^\prime}^{-} = \{t \in \mathbb{R} \, : \, t^\prime + \Delta_t < t \le T\}\)

사전 학습된 모델 \(\textbf{f}_{\theta_0}\)를 사용하여 경계 조건을 효과적으로 적용하려면 \(\psi_t\)에서 샘플링된 무시할 수 없는 양의 $t$가 간격 \(S_{t^\prime}\) 내에 있어야 한다. 그렇지 않으면 연속적인 timestep $t$와 \(t - \Delta_t\)가 대부분 $t^\prime$보다 크거나 같아 사전 학습된 모델의 영향이 제한된다.

이 시간 분할과 새로운 parameterization을 통해 \(\mathcal{L}_\textrm{CT}\)는 다음과 같이 분해될 수 있다.

\[\begin{aligned} \mathcal{L}_\textrm{CT} (\textbf{f}_{\theta, \theta_0^{-}}^\textrm{trunc}, \textbf{f}_{\theta^{-}, \theta_0^{-}}^\textrm{trunc}) &= \underbrace{\int_{t \in S_{t^\prime}} \psi_t (t) \frac{\omega (t)}{\Delta_t} d (\textbf{f}_\theta (\textbf{x} + t \boldsymbol{\epsilon}, t), \textbf{f}_{\theta_0^{-}} (\textbf{x} + (t - \Delta_t) \boldsymbol{\epsilon}, t - \Delta_t)) dt}_{\textrm{Boundary loss}} \\ &+ \underbrace{\int_{t \in S_{t^\prime}^{-}} \psi_t (t) \frac{\omega (t)}{\Delta_t} d (\textbf{f}_\theta (\textbf{x} + t \boldsymbol{\epsilon}, t), \textbf{f}_{\theta^{-}} (\textbf{x} + (t - \Delta_t) \boldsymbol{\epsilon}, t - \Delta_t)) dt}_{\textrm{Consistency loss}} \end{aligned}\]

(간단한 표기를 위해 \(\textbf{x} \sim p_\textrm{data}\)와 \(\boldsymbol{\epsilon} \sim \mathcal{N}(0,\textbf{I})\)에 대한 기대값 계산은 생략)

일반적인 consistency training과 달리 TCM은 boundary loss와 consistency loss라는 두 가지 항을 갖는다. Boundary loss는 모델이 사전 학습된 모델로부터 학습할 수 있도록 하여 상수로의 붕괴를 방지한다.

\(S_{t^\prime}^{-}\)에서 충분한 시간 $t$를 샘플링하지 않아 경계 조건을 충분히 활용하지 않으면 위 objective에 대한 학습이 여전히 상수로 붕괴될 수 있다. 특히 consistency training이 수렴에 가까워 $\Delta_t$가 0에 가까울 때 이런 일이 발생할 수 있다. 저자들은 이를 방지하기 위해 \(\int_{t \in S_{t^\prime}} \psi_t (t) dt > 0\)을 만족하도록 \(\psi_t\)를 설계하였다. 즉, \(\Delta_t\)가 0에 가까울 때에도 \(S_{t^\prime}^{-}\)의 한 지점을 샘플링할 엄격한 양의 확률이 있다. 구체적으로 \(\psi_t\)를 $t^\prime$에서의 디랙 델타 함수 $\delta (\cdot)$와 다른 분포 \(\bar{\psi}_t (t)\)의 혼합으로 정의한다.

\[\begin{equation} \psi_t (t) = \lambda_b \delta(t - t^\prime) + (1 - \lambda_b) \bar{\psi}_t (t) \end{equation}\]

(\(\lambda_b \in (0, 1)\)는 가중 계수, \(bar{\psi}_t\)는 $(t^\prime, T]$에서 정의됨)

\(\int_{t \in S_{t^\prime}} \psi_t (t) dt \ge \lambda_b\)이고 \(\lambda_b\)는 경계 조건을 얼마나 강조할지 제어한다.

첫 번째 단계에서 consistency model이 $[0, t^\prime]$에서 완벽하게 학습되었다고 가정하자 (즉, 모든 $t \in [0, t^\prime]$에 대해 \(\textbf{f}_{\theta_0} (\textbf{x}_t, t) = \textbf{x}_0\)). 만일 \(\textbf{f}_\theta (\textbf{x}_{t^\prime}, t^\prime) \ne \textbf{f}_{\theta_0} (\textbf{x}_{t^\prime}, t^\prime)\)이면 \(\textbf{f}_\theta\)는 boundary loss로 인해 페널티를 받는다. Boundary loss를 최소화하면 \(\textbf{f}_\theta\)에서 경계 조건이 적용되고,

\[\begin{equation} \textbf{f}_\theta (\textbf{x}_{t^\prime}, t^\prime) = \textbf{f}_{\theta_0} (\textbf{x}_{t^\prime}, t^\prime) = \textbf{x}_0 \end{equation}\]

consistency loss를 최소화하면 경계 조건이 $t = T$까지 전파된다.

\[\begin{equation} \textbf{f}_\theta (\textbf{x}_T, T) = \textbf{f}_\theta (\textbf{x}_{t^\prime}, t^\prime) \end{equation}\]

결과적으로, loss는 모델을 \(\textbf{f}_\theta (\textbf{x}_T, T) = \textbf{x}_0\)로 효과적으로 가이드한다. 앞서 정의한 시간 분포 \(\psi_t\)를 사용하면 학습 loss는 다음과 같다.

\[\begin{aligned} \mathcal{L}_\textrm{CT} (\textbf{f}_{\theta, \theta_0^{-}}^\textrm{trunc}, \textbf{f}_{\theta^{-}, \theta_0^{-}}^\textrm{trunc}) &\approx \underbrace{\lambda_b \frac{\omega (t^\prime)}{\Delta_{t^\prime}} d (\textbf{f}_\theta (\textbf{x} + t^\prime \boldsymbol{\epsilon}, t^\prime), \textbf{f}_{\theta_0^{-}} (\textbf{x} + (t^\prime - \Delta_{t^\prime}) \boldsymbol{\epsilon}, t^\prime - \Delta_{t^\prime}))}_{\textrm{Boundary loss} := \mathcal{L}_B (\textbf{f}_\theta, \textbf{f}_{\theta_0^{-}})} \\ &+ (1 - \lambda_b) \underbrace{\mathbb{E}_{\bar{\psi}_t} [\frac{\omega (t)}{\Delta_t} d (\textbf{f}_\theta (\textbf{x} + t \boldsymbol{\epsilon}, t), \textbf{f}_{\theta^{-}} (\textbf{x} + (t - \Delta_t) \boldsymbol{\epsilon}, t - \Delta_t))]}_{\textrm{Consistency loss} := \mathcal{L}_C (\textbf{f}_\theta, \textbf{f}_{\theta^{-}})} \end{aligned}\]

이 근사는 truncated consistency training에서 \(\Delta_t\)가 충분히 작기 때문에 성립한다. \((1 − \lambda_b)\)를 \(\lambda_b\)에 흡수하면 최종 학습 loss는 다음과 같이 표현된다.

\[\begin{equation} \mathcal{L}_\textrm{TCM} = w_b \mathcal{L}_B (\textbf{f}_\theta, \textbf{f}_{\theta_0^{-}}) + \mathcal{L}_C (\textbf{f}_\theta, \textbf{f}_{\theta^{-}}) \\ \textrm{where} \quad w_b = \frac{\lambda_b}{1 - \lambda_b} \end{equation}\]

두 loss를 추정하기 위해 크기 $B$의 각 mini-batch를 두 개의 부분 집합으로 분할한다. Boundary loss \(\mathcal{L}_B\)는 $N_B = \lfloor \rho B \rfloor$개의 샘플을 사용하여 추정한다 ($\rho \in (0,1)$는 hyperparameter). Consistency loss \(\mathcal{L}_C\)는 나머지 $B − N_B$개의 샘플을 사용하여 추정한다. $\rho$를 증가시키면 boundary loss gradient 추정량의 분산은 감소하지만 consistency loss gradient 추정량의 분산은 증가하고, 그 반대의 경우도 마찬가지이다.

최종 mini-batch loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{TCM} \approx \frac{w_b}{N_B} \sum_{i=1}^{N_B} \nabla_\theta (\mathcal{L}_B)_i (\textbf{f}_\theta, \textbf{f}_{\theta_0^{-}}) + \frac{1}{B - N_B} \sum_{j = N_B + 1}^B \nabla_\theta (\mathcal{L}_C)_j (\textbf{f}_\theta, \textbf{f}_{\theta^{-}}) \end{equation}\]

(\((\mathcal{L}_B)_i\)는 $\delta (t - t^\prime)$에서의 $i$번째 샘플에 대한 boundary loss, \((\mathcal{L}_C)_j\)는 \(\bar{\psi}_t\)에서의 $j$번째 샘플에 대한 consistency loss)

Experiments

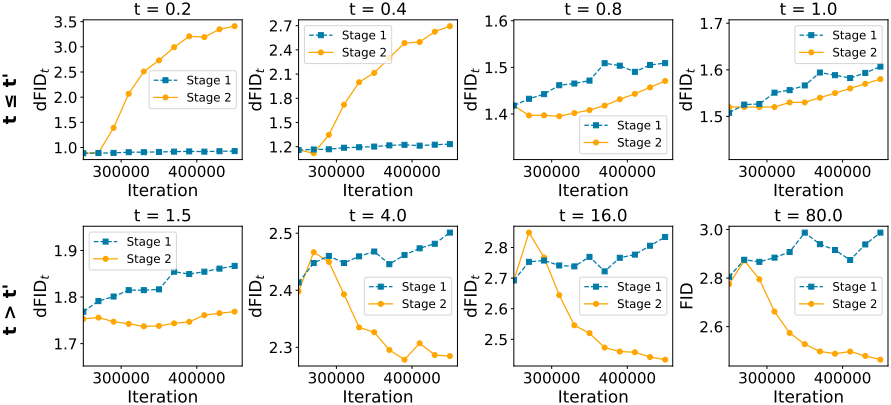
1. Truncated training allocates capacity toward generation

다음은 학습에 따른 denoising FID (dFID)의 변화를 학습 단계에 대하여 비교한 그래프이다.

2. TCM improves the sample quality of consistency models

다음은 (왼쪽) CIFAR-10과 (오른쪽) ImageNet 64$\times$64에서 다른 방법들과 비교한 결과이다.

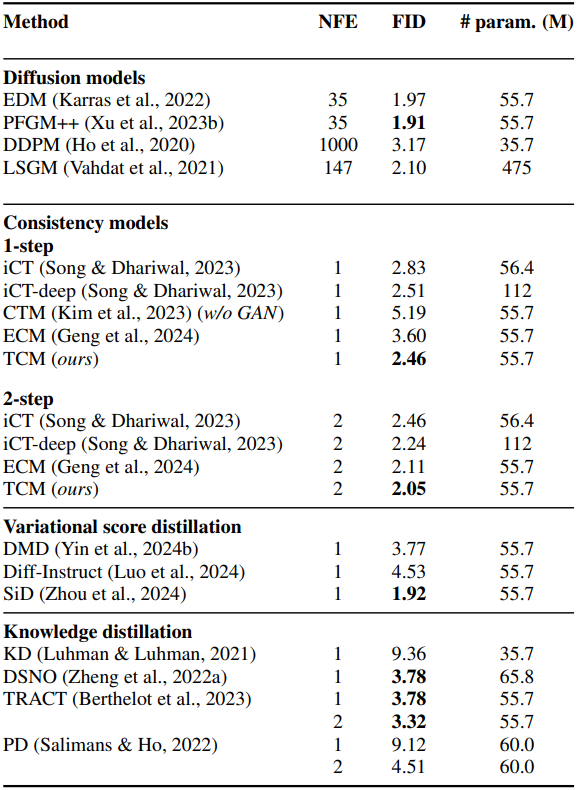
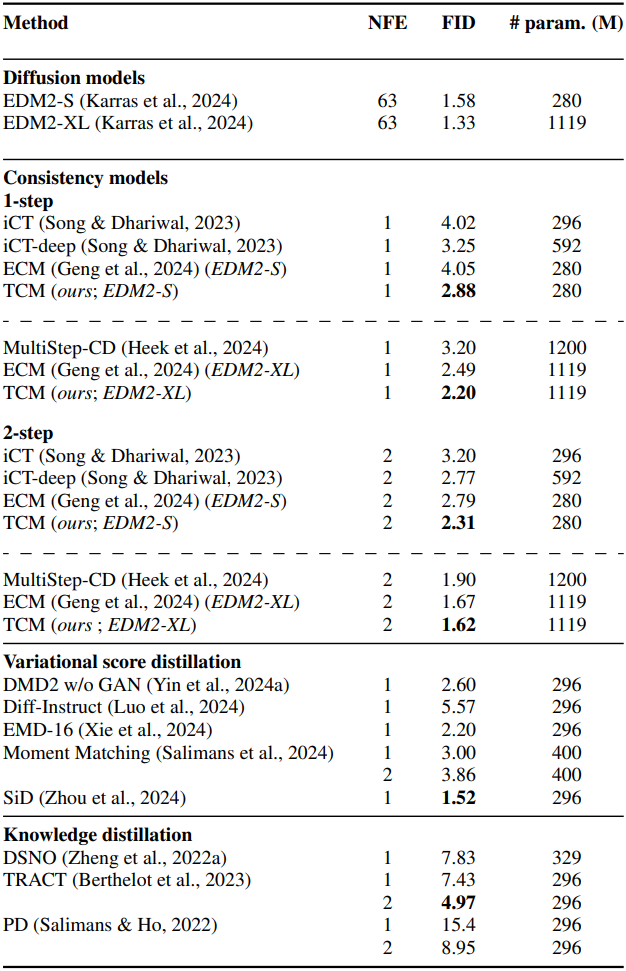
다음은 1-step과 2-step으로 생성한 샘플들의 예시이다.

3. Analyses of design choices

다음은 hyperparameter에 대한 ablation 결과이다.

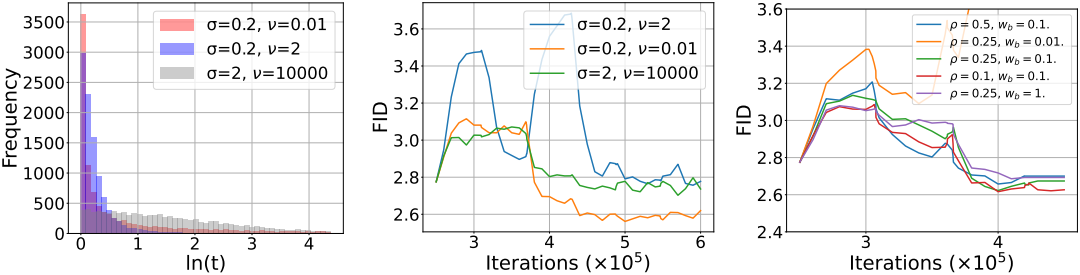
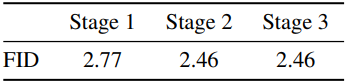
다음은 $t^\prime$에 대한 CIFAR-10 FID를 비교한 표이다.

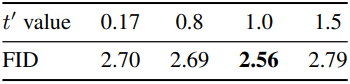
다음은 $t^\prime = 4$를 기준으로 3번째 학습 단계를 추가하였을 때의 결과이다.