[논문리뷰] Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

ICCV 2021. [Paper] [Github]
Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, Baining Guo
Microsoft Research Asia
25 Mar 2021

Introduction

컴퓨터 비전의 모델링은 오랫동안 CNN에 의해 지배되었다. AlexNet과 ImageNet image classification 챌린지에 대한 혁신적인 성능을 시작으로 CNN 아키텍처는 더 큰 스케일, 더 광범위한 연결, 더 정교한 convolution 형식을 통해 점점 더 강력해졌다. 다양한 비전 task를 위한 backbone 네트워크 역할을 하는 CNN과 함께 이러한 아키텍처의 발전은 전체 분야를 광범위하게 끌어올린 성능 향상으로 이어졌다.

반면에 자연어 처리(NLP)에서 네트워크 아키텍처의 진화는 오늘날 널리 사용되는 아키텍처가 Transformer인 다른 경로를 택했다. 시퀀스 모델링 및 변환 task를 위해 설계된 Transformer는 데이터의 장거리 의존성 (long-range dependency)을 모델링하는 데 attention을 사용하는 것으로 유명하다. 언어 도메인에서의 엄청난 성공으로 연구자들은 컴퓨터 비전에 대한 Transformer를 조사하게 되었으며, 최근 특정 tak, 특히 image classification 분류와 비전-언어 공동 모델링에 대한 유망한 결과를 보여주었다.

본 논문은 Transformer가 NLP에서, CNN이 비전에서 하는 것처럼 컴퓨터 비전을 위한 범용 backbone 역할을 할 수 있도록 Transformer의 적용 가능성을 확장하고자 한다. 저자들은 언어 도메인에서 비전 영역으로 고성능을 전환하는 데 있어 중요한 문제가 두 modality 간의 차이로 설명될 수 있음을 관찰했습다. 이러한 차이점 중 하나는 스케일과 관련이 있다. 언어 Transformer에서 처리의 기본 요소 역할을 하는 단어 토큰과 달리 시각적 요소는 스케일이 상당히 다를 수 있다. 기존 Transformer 기반 모델에서 토큰은 모두 고정된 스케일이며 이러한 비전 애플리케이션에 적합하지 않은 속성이다.

또 다른 차이점은 텍스트 구절의 단어에 비해 이미지의 픽셀 해상도가 훨씬 더 높다는 것이다. 픽셀 레벨에서 조밀한 예측을 필요로 하는 semantic segmentation과 같은 많은 비전 task가 존재하며, self-attention의 계산 복잡도가 이미지 크기의 제곱에 비례하기 때문에 고해상도 이미지에서 Transformer의 경우 처리하기 어렵다.

이러한 문제를 극복하기 위해 본 논문은 계층적 feature map을 구성하고 이미지 크기에 대한 선형 계산 복잡도를 갖는 Swin Transformer라는 범용 Transformer backbone을 제안하였다.

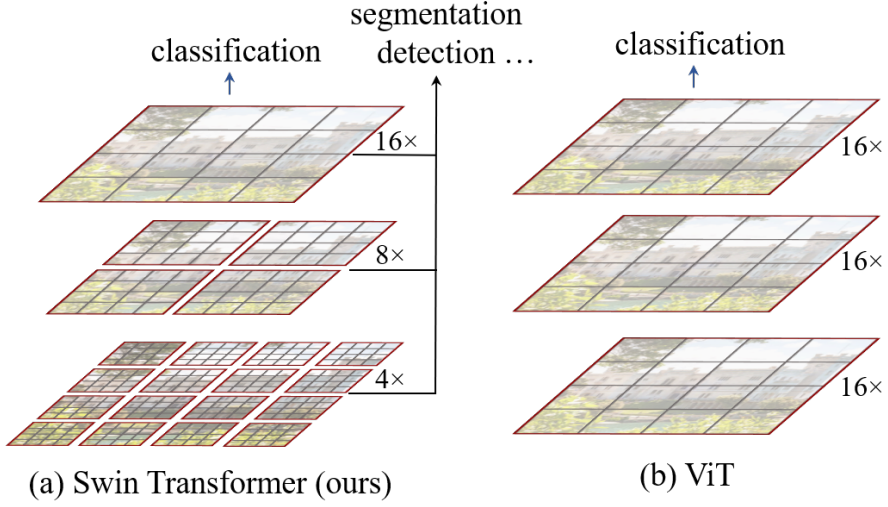
위 그림과 같이 Swin Transformer는 작은 크기의 패치 (회색 윤곽선)에서 시작하여 점점 더 깊은 Transformer 레이어에서 인접한 패치를 병합하여 계층적 표현을 구성한다. 이러한 계층적 feature map을 통해 Swin Transformer 모델은 feature pyramid network (FPN) 또는 U-Net과 같은 조밀한 예측을 위한 고급 기술을 편리하게 활용할 수 있다.

이미지를 분할하는 겹치지 않는 window (빨간색 윤곽선) 내에서 로컬로 self-attention을 계산하여 선형 계산 복잡도를 달성된다. 각 window의 패치 수는 고정되어 있으므로 복잡도는 이미지 크기에 비례한다. 이러한 장점으로 인해 Swin Transformer는 단일 해상도의 feature map을 생성하고 2차 복잡도를 갖는 이전 Transformer 기반 아키텍처와 달리 다양한 비전 task를 위한 범용 backbone으로 적합하다.

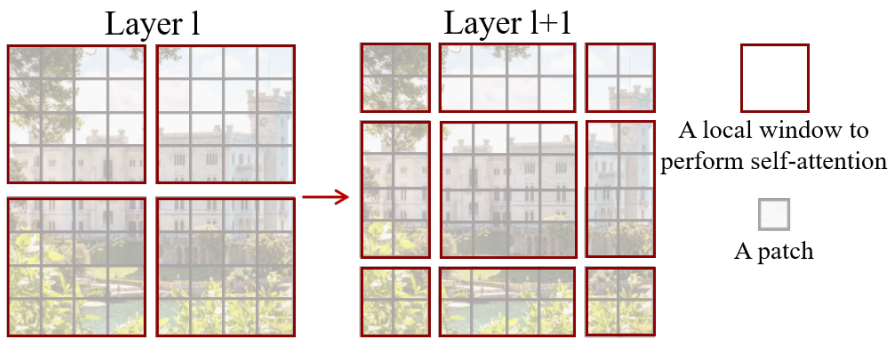
Swin Transformer의 핵심 설계 요소는 위 그림과 같이 연속적인 self-attention 레이어 사이의 window 파티션의 이동이다. Shifted window는 이전 레이어의 window를 연결하여 모델링 능력을 크게 향상시키는 연결을 제공한다. 이 전략은 또한 실제 지연 시간과 관련하여 효율적이다. Window 내의 모든 쿼리 패치는 하드웨어에서 메모리 액세스를 용이하게 하는 동일한 키 세트를 공유한다.

대조적으로 이전의 슬라이딩 window 기반 self-attention 접근 방식은 다른 쿼리 픽셀에 대한 다른 키 세트로 인해 일반 하드웨어에서 낮은 지연 시간으로 어려움을 겪고 있다. 제안된 shifted window 방식이 sliding window 방식보다 지연 시간이 훨씬 짧지만 모델링 능력은 비슷하다. 또한 shfted window 접근 방식은 모든 MLP 아키텍처에도 유익하다.

Method

1. Overall Architecture

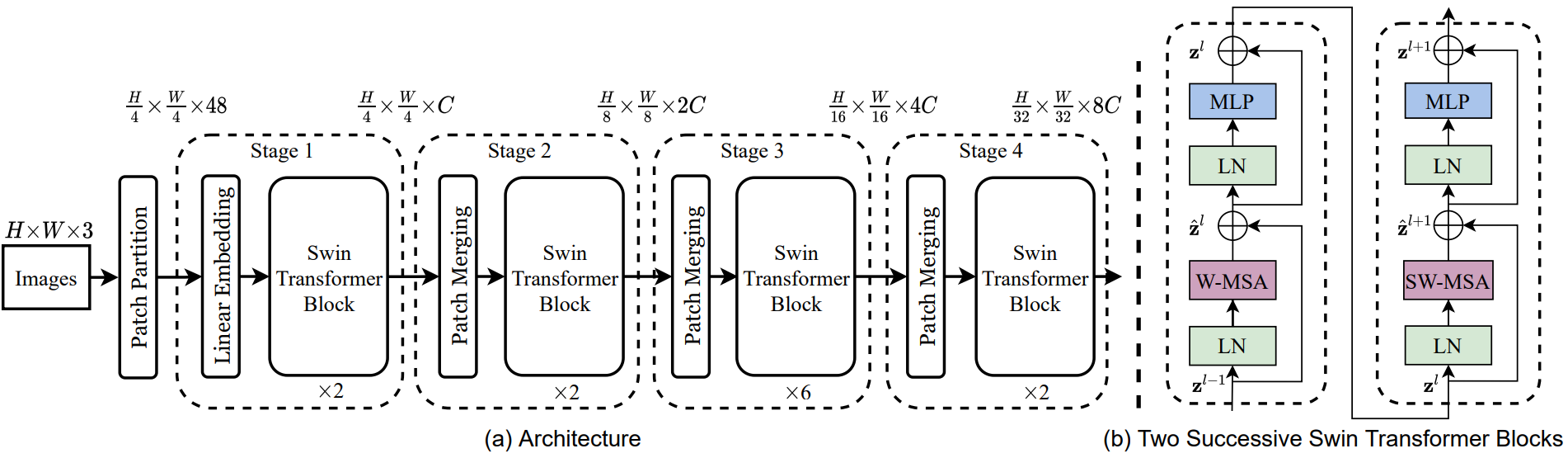
Swin Transformer 아키텍처의 개요는 tiny 버전인 SwinT를 보여주는 위 그림에 나와 있다. 먼저 ViT와 같은 패치 분할 모듈에 의해 입력 RGB 이미지를 겹치지 않는 패치로 분할한다. 각 패치는 “토큰”으로 취급되며 해당 feature는 픽셀 RGB 값의 concatenation으로 설정된다. 구현에서는 4$\times$4의 패치 크기를 사용하므로 각 패치의 feature 차원은 $4 \times 4 \times 3 = 48$이다. 이 feature에 선형 임베딩 레이어를 적용하여 임의의 차원 $C$로 project한다.

수정된 self-attention 계산(Swin Transformer 블록)이 포함된 여러 Transformer 블록이 이러한 패치 토큰에 적용된다. Transformer 블록은 토큰 수 ($\frac{H}{4} \times \frac{W}{4}$)를 유지하며 선형 임베딩과 함께 “1단계”라고 부른다.

계층적 표현을 생성하기 위해 네트워크가 깊어짐에 따라 레이어를 패치 병합하여 토큰 수를 줄인다. 첫 번째 패치 병합 레이어는 2$\times$2 인접 패치의 각 그룹의 feature를 concat하고 $4C$ 차원의 concat된 feature에 linear layer를 적용한다. 이렇게 하면 4의 배수만큼 토큰 수가 줄어들고 출력 차원은 $2C$로 설정된다. Swin Transformer 블록은 $\frac{H}{8} \times \frac{W}{8}$에서 해상도를 유지하면서 feature 변환을 위해 나중에 적용된다. 이 패치 병합 및 feature 변환의 첫 번째 블록은 “2단계”로 부른다. 이 절차는 각각 $\frac{H}{16} \times \frac{W}{16}$과 $\frac{H}{32} \times \frac{W}{32}$의 출력 해상도로 “3단계”와 “4단계”로 두 번 반복된다. 이러한 단계는 일반적인 convolution network (ex. VGG, ResNet)와 동일한 feature map 해상도로 계층적 표현을 공동으로 생성한다. 결과적으로 제안하는 아키텍처는 다양한 비전 task를 위해 기존 방식의 backbone 네트워크를 편리하게 대체할 수 있다.

Swin Transformer block

Swin Transformer는 Transformer 블록의 multi-head self-attention (MSA) 모듈을 shifted window를 기반으로 하는 모듈로 교체하고 다른 레이어는 동일하게 유지함으로써 구축된다. Swin Transformer 블록은 shifted window 기반 MSA 모듈과 중간에 GELU nonlinearity가 있는 2-layer MLP로 구성된다. LN (LayerNorm) layer는 각 MSA 모듈과 각 MLP 이전에 적용되고 residual connection은 각 모듈 이후에 적용된다.

2. Shifted Window based Self-Attention

표준 Transformer 아키텍처와 image classification을 위한 버전은 토큰과 다른 모든 토큰 간의 관계가 계산되는 글로벌 self-attention을 수행한다. 글로벌 계산은 토큰 수와 관련하여 2차 복잡도를 초래하여 조밀한 예측이나 고해상도 이미지를 나타내기 위해 막대한 토큰 세트가 필요한 많은 비전 문제에 적합하지 않다.

Self-attention in non-overlapped windows

본 논문은 효율적인 모델링을 위해 로컬한 window 내에서 self-attention을 계산할 것을 제안한다. Window는 겹치지 않는 방식으로 이미지를 균등하게 분할하도록 배열된다. 각 window에 $M \times M$개의 패치가 포함되어 있다고 가정하면 글로벌 MSA 모듈의 계산 복잡도와 $h \times w$ 패치 이미지를 기반으로 하는 window의 계산 복잡도는 다음과 같다.

\[\begin{equation} \Omega (\textrm{MSA}) = 4hwC^2 + 2(hw)^2 C \\ \Omega (\textrm{W-MSA}) = 4hw C^2 + 2 M^2 hw C \end{equation}\]

여기서 MSA는 패치 수 $hw$에 대해 2차이고 W-MSA는 M이 고정된 경우 (default는 7) 선형이다. 글로벌 self-attention 계산은 일반적으로 큰 $hw$에 적합하지 않은 반면 window 기반 self-attention은 확장 가능하다.

Shifted window partitioning in successive blocks

Window 기반 self-attention 모듈은 window 간의 연결이 부족하여 모델링 능력이 제한된다. 저자들은 겹치지 않는 창의 효율적인 계산을 유지하면서 window 사이의 연결을 도입하기 위해 연속되는 Swin Transformer 블록에서 두 개의 파티션 구성을 번갈아 가며 전환하는 shifted window 파티셔닝 방식을 제안하였다.

첫 번째 모듈은 왼쪽 상단 픽셀에서 시작하는 일반적인 window 분할 전략을 사용하고 8$\times$8 feature map은 크기가 4$\times$4 ($M = 4$)인 2$\times$2 창으로 고르게 분할된다. 그러면 다음 모듈은 규칙적으로 분할된 window에서 $(\lfloor \frac{M}{2} \rfloor, \lfloor \frac{M}{2} \rfloor)$ 픽셀만큼 window를 대체하여 이전 레이어의 구성에서 shifted window 구성을 채택한다. Shifted window 파티셔닝 접근 방식을 사용하면 연속되는 Swin Transformer 블록이 다음과 같이 계산된다.

\[\begin{equation} \hat{z}^l = \textrm{W-MSA} (\textrm{LN} (z^{l-1})) + z^{l-1} \\ z^l = \textrm{MLP} (\textrm{LN} (\hat{z}^l)) + \hat{z}^l \\ \hat{z}^{l+1} = \textrm{SW-MSA} (\textrm{LN} (z^l)) + z^l \\ z^{l+1} = \textrm{MLP} (\textrm{LN} (\hat{z}^{l+1})) + \hat{z}^{l+1} \\ \end{equation}\]

여기서 $\hat{z}^l$과 $z^l$은 각각 블록 $l$에 대한 (S)W-MSA 모듈과 MLP 모듈의 출력 feature를 나타낸다. W-MSA와 SW-MSA는 각각 일반 및 shfted window 파티션 구성을 사용하는 window 기반 MSA를 나타낸다.

Shifted window 파티셔닝 접근법은 이전 레이어에서 인접한 겹치지 않는 window 사이의 연결을 도입하고 image classification, object detection, semantic segmentation에 효과적이다.

Efficient batch computation for shifted configuration

Shifted window 파티셔닝의 문제는 더 많은 window를 만들며, 일부 창은 $M \times M$보다 작아야 한다.

\[\begin{equation} \lceil \frac{h}{M} \rceil \times \lceil \frac{w}{M} \rceil \rightarrow \bigg( \lceil \frac{h}{M} \rceil + 1 \bigg) \times \bigg( \lceil \frac{w}{M} \rceil + 1 \bigg) \end{equation}\]

Naive한 해결책은 attention을 계산할 때 더 작은 window를 $M \times M$ 크기로 채우고 패딩된 값을 마스킹하는 것이다. 일반 파티셔닝의 window 수가 적은 경우, 이 naive한 솔루션으로 증가된 계산은 상당하다. 예를 들어 2$\times$2의 경우 3$\times$3이 되어 window 수가 2.25배 커진다.

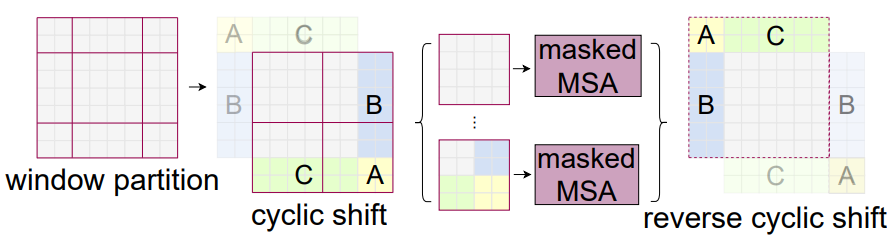
본 논문은 위 그림과 같이 왼쪽 위 방향으로 순환 이동 (cyclic-shifting)하여 보다 효율적인 배치 계산 방식을 제안한다. 이 이동 후 일괄 처리된 window는 feature map에서 인접하지 않은 여러 개의 하위 window로 구성될 수 있다. 따라서 마스킹 메커니즘을 사용하여 각 하위 window 내에서 self-attention 계산을 제한한다. Cyclic-shifting를 사용하면 배치된 window의 수가 일반 window 파티션과 동일하게 유지되므로 효율적이다.

Relative position bias

Self-attention 계산에서 각 head에 대한 상대적 위치 바이어스 $B \in \mathbb{R}^{M^2 \times M^2}$을 포함한다.

\[\begin{equation} \textrm{Attention} (Q, K, V) = \textrm{SoftMax} (\frac{QK^\top}{\sqrt{d}} + B) V \end{equation}\]

여기서 $Q, K, V \in \mathbb{R}^{M^2 \times d}$는 각각 query, key, value 행렬이며 $d$는 query와 key의 차원이다. $M^2$은 window의 패치 수이다. 각 축을 따라 상대적 위치가 $[-M+1, M-1]$ 범위에 있기 때문에 더 작은 크기의 바이어스 행렬 $\hat{B} \in \mathbb{R}^{(2M−1) \times (2M−1)}$을 parameterize하고 $B$의 값은 $\hat{B}$에서 가져온다.

사전 학습 시 학습된 상대적 위치 바이어스는 bi-cubic interpolation을 통해 다른 window 크기의 fine-tuning을 위한 모델을 초기화하는 데에도 사용할 수 있다.

3. Architecture Variants

저자들은 ViT-B/DeiT-B와 유사한 모델 크기와 계산 복잡도를 갖도록 Swin-B라는 기본 모델을 구축하였다. 또한 모델 크기와 계산 복잡도가 각각 약 0.25배, 0.5배, 2배인 버전인 Swin-T, Swin-S, Swin-L을 도입한다. Swin-T와 Swin-S의 복잡도는 각각 ResNet-50 (DeiT-S)과 ResNet-101의 복잡도와 유사하다. Window 크기는 기본적으로 $M = 7$로 설정된다. 모든 실험에서 각 head의 query 차원은 $d = 32$이고 각 MLP의 expansion layer은 $\alpha = 4$이다. 이러한 모델 변형의 아키텍처 hyperparameter는 다음과 같다.

1. Swin-T: $C$ = 96, layer 수 = {2, 2, 6, 2}
2. Swin-S: $C$ = 96, layer 수 = {2, 2, 18, 2}
3. Swin-B: $C$ = 128, layer 수 = {2, 2, 18, 2}
4. Swin-L: $C$ = 192, layer 수 = {2, 2, 18, 2}

여기서 $C$는 1단계에 있는 hidden layer의 채널 수다.

Experiments

• 데이터셋
  • ImageNet-1K image classification
  • COCO object detection
  • ADE20K semantic segmentation

1. Image Classification on ImageNet-1K

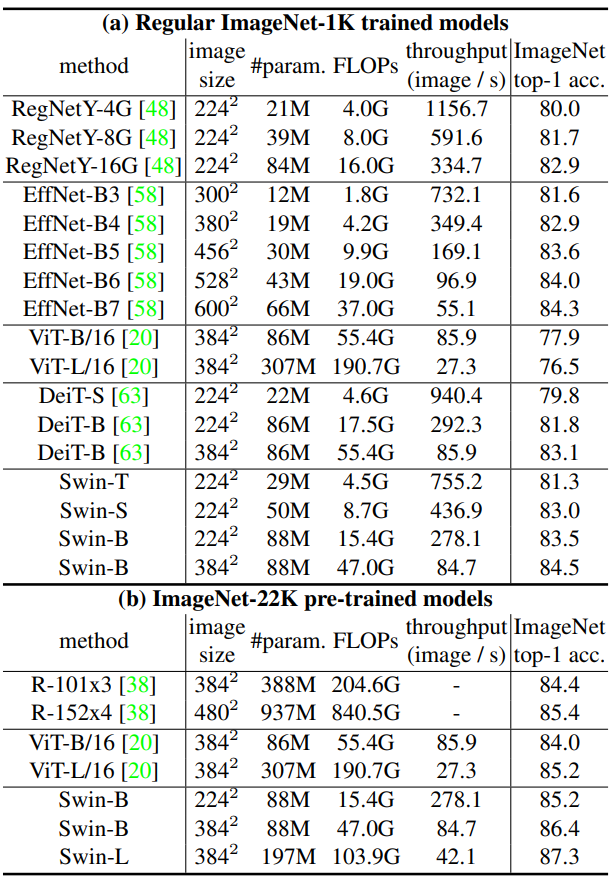
2. Object Detection on COCO

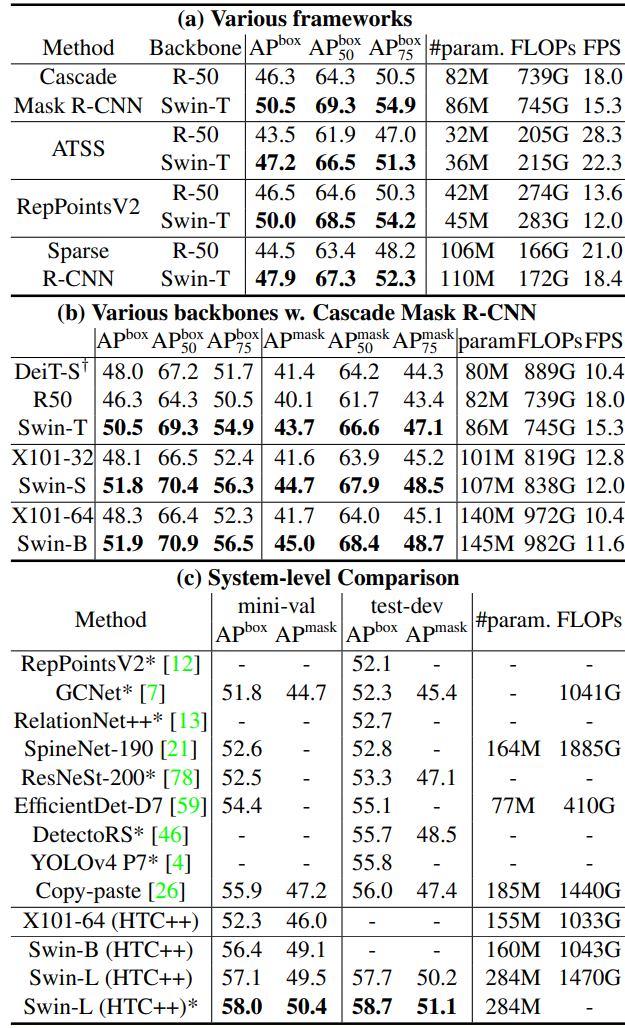
3. Semantic Segmentation on ADE20K

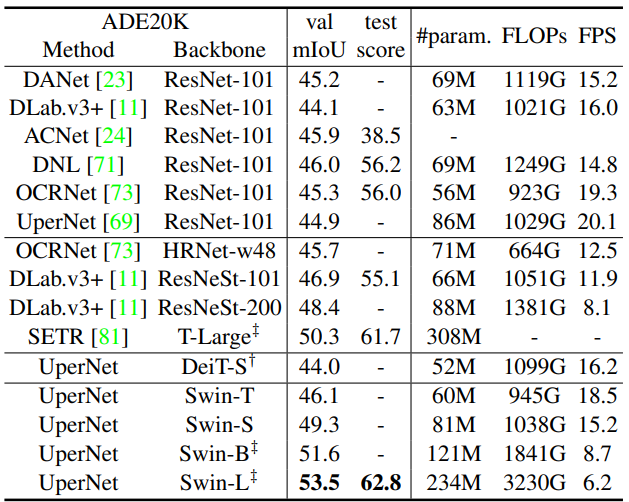
4. Ablation Study

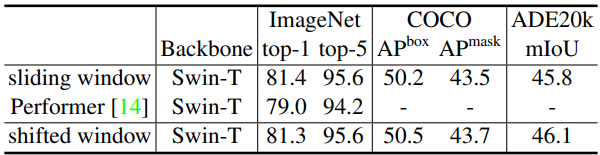
다음은 shifted window 접근법과 다양한 위치 임베딩 방법에 대한 ablation study 결과이다. (Swin-T 아키텍처)

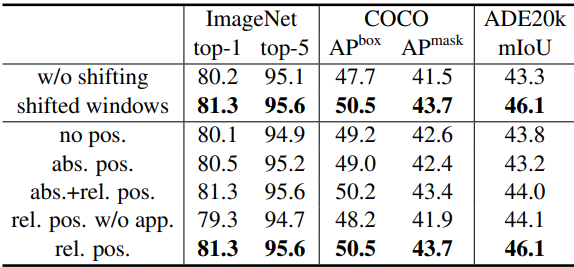
다음은 다양한 self-attention 계산 방법에 대한 실제 속도를 비교한 표이다.

다음은 다양한 self-attention 계산 방법을 사용한 Swin Transformer의 정확도를 비교한 표이다.