Diffusion은 신이고 GPT는 무적이다

CVPR 2025. [Paper] [Page] [Github]
Cheng Sun, Jaesung Choe, Charles Loop, Wei-Chiu Ma, Yu-Chiang Frank Wang
NVIDIA | Cornell University | National Taiwan University
5 Dec 2024

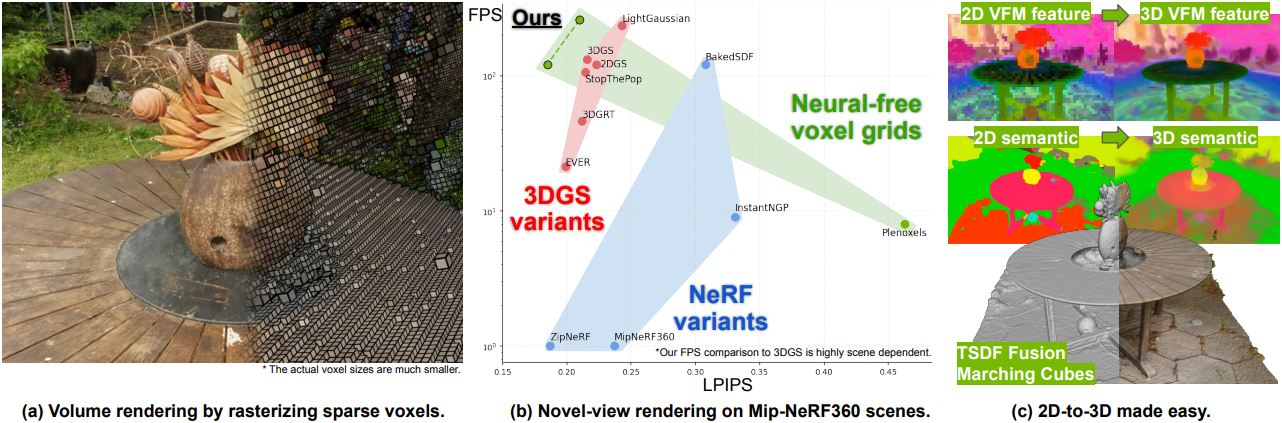
Introduction

3D Gaussian Splatting (3DGS)은 뛰어난 렌더링 속도와 장면의 미묘한 디테일을 포착하는 능력을 가지고 있지만, 두 가지 주요 한계점이 있다.

  1. Gaussian을 중심을 기준으로 정렬해도 적절한 깊이 순서가 보장되지 않는다. 뷰를 변경할 때 팝핑 아티팩트(갑작스러운 색상 변경)가 발생할 수 있다.
  2. 3D 포인트의 volume density는 여러 Gaussian으로 덮여 있을 때 잘 정의되지 않는다. 이러한 모호성으로 인해 표면 재구성이 쉽지 않다.

반면, 그리드 표현은 본질적으로 이러한 문제를 피하며, 순서와 볼륨이 모두 잘 정의되어 있다. 그러나 ray casting으로 인해 렌더링 속도가 3DGS보다 느리다. 본 논문은 두 방법의 장점을 모두 취하여, 즉 3DGS의 효율성을 잘 정의된 그리드 속성과 결합하는 것에 초점을 맞추었다.

저자들의 핵심 통찰력은 voxel을 사용하는 것이다. Voxel 표현은 본질적으로 현대 그래픽 엔진과 호환되며 효율적으로 rasterization할 수 있다. 또한 volume ray casting을 통해서도 volume density를 모델링할 수 있다. 그러나 장면은 여러 level of detail로 구성될 수 있기 때문에, 단순하게 voxel을 사용하는 것은 잘 작동하지 않는다.

저자들은 3DGS의 rasterization 효율성과 그리드 기반 표현의 구조화된 접근 방식을 결합한 새로운 프레임워크인 SVRaster를 제시하였다. SVRaster는 여러 레벨의 sparse voxel을 활용하여 3D 장면을 모델링하고, 적응형 크기의 sparse voxel 표현에서 rasterization 렌더링을 용이하게 하는 방향에 따른 Morton order 인코딩을 사용한다.

SVRaster는 3D 공간이 분리된 voxel로 분할되고 정렬을 통해 올바른 렌더링 순서가 보장되므로 팝핑 아티팩트가 없다. 또한, TSDF Fusion과 Marching Cubes 등 기존 그리드 기반 3D 처리 알고리즘과 쉽고 원활하게 통합될 수 있다.

SVRaster는 빠르게 학습되고, 빠르게 렌더링되며, SOTA와 비슷한 수준의 렌더링 품질을 보여준다. 또한, 학습된 sparse voxel 그리드에서 sparse-voxel TSDF-Fusion과 sparse-voxel Marching Cubes를 통해 메쉬를 추출할 수 있으며, 표면 정확도와 처리 속도 간의 좋은 균형을 보여준다.

Approach

1. Sparse Voxels Rasterization

NeRF나 3DGS와 같은 radiance field 렌더링 방법과 동일하게, 픽셀의 색상 $C$를 렌더링하기 위해 다음과 같은 알파 블렌딩을 사용한다.

\[\begin{equation} C = \sum_{i=1}^N T_i \cdot \alpha_i \cdot c_i, \quad T_i = \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]

(\(\alpha_i \in \mathbb{R}_{\in [0,1]}\)와 \(c_i \in \mathbb{R}_{\in [0,1]}^3\)는 픽셀 광선의 $i$번째 샘플링된 포인트 또는 primitive의 alpha와 색상, $T_i$는 투과율)

알파 블렌딩을 위한 장면 표현을 위해서는 두 가지를 결정해야 한다.

  1. 어떻게 $N$개의 포인트 또는 primitive를 찾을 것인가?
  2. 장면 표현에서 RGB 값과 alpha 값을 어떻게 결정할 것인가?

Scene Representation

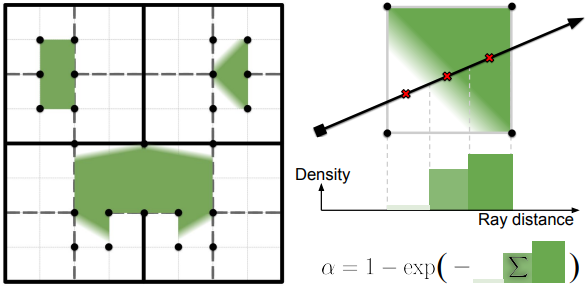
Sparse voxel grid

SVRaster는 sparse voxel 표현을 사용하여 3D 장면을 구성한다. Voxel은 Octree layout에 따라 할당되는데, 이는 고품질 결과를 얻는 데 필요한 두 가지 이유 때문이다.

  1. 다양한 크기의 voxel을 올바르게 렌더링하는 데 도움이 된다.
  2. Sparse voxel을 다양한 level-of-detail에 적응적으로 맞출 수 있다.

이 표현은 부모-자식 포인터나 linear Octree를 사용하는 기존 Octree 데이터 구조를 사용하지 않는다. 구체적으로, 조상 노드가 없는 Octree 리프 노드에만 voxel을 보관한다. 이러한 정렬 기반 rasterizer는 voxel을 이미지 공간에 projection하고 렌더링할 때 모든 voxel이 올바른 순서로 정렬되도록 보장한다. 즉, rasterizer가 제공하는 유연성 덕분에 더 복잡한 데이터 구조를 유지할 필요 없이 임의의 순서로 개별 voxel을 저장한다.

저자들은 최대 그리드 해상도를 $(2^L)^3$로 정의하는 최대 level of detail $L = 16$을 선택하였다. \(\textbf{w}_s \in \mathbb{R}\)와 \(\textbf{w}_c \in \mathbb{R}^3\)를 각각 world space에서의 Octree 크기와 Octree 중심이라고 하자. Voxel 인덱스 \(v = \{i, j, k\} \in [0, \ldots, 2^L - 1]^3\)와 Octree 레벨 $l \in [1,L]$에 대한 voxel 크기 \(\textbf{v}_s\)와 voxel 중심 \(\textbf{v}_c\)는 다음과 같이 정의된다.

\[\begin{equation} \textbf{v}_s = \textbf{w}_s \cdot 2^{-l}, \quad \textbf{v}_c = \textbf{w}_c - 0.5 \cdot \textbf{w}_s + \textbf{v}_s \cdot v \end{equation}\]

(루트 노드 $l = 0$은 사용되지 않음)

Voxel alpha

장면 형상의 경우 voxel 모서리에 해당하는 8개의 파라미터 \(\textbf{v}_\textrm{geo} \in \mathbb{R}^{2 \times 2 \times 2}\)를 사용하여 각 voxel 내부의 density field를 trilinear하게 모델링한다. 인접한 voxel 간에 모서리를 공유하면 연속적인 density field가 생성된다.

또한 \(\textbf{v}_\textrm{geo}\)의 density가 0보다 크거나 값을 가지도록 보장하기 위해 activation function이 필요하다. 이를 위해 exponential-linear activation을 사용한다.

\[\begin{equation} \textrm{explin} (x) = \begin{cases} x & \textrm{if} \; x > 1.1 \\ \exp (\frac{x}{1.1} - 1 + \textrm{log} 1.1) & \textrm{otherwise} \end{cases} \end{equation}\]

이 activation function은 softplus를 근사하지만 계산이 더 효율적이다. Voxel 내부의 선명한 density field를 위해, trilinear interpolation 후에 activation을 적용한다.

알파 블렌딩에 기여하는 voxel의 alpha 값을 도출하기 위해, 광선-voxel 교차점의 세그먼트에서 $K$개의 포인트를 균등하게 샘플링한다. 이 방정식은 NeRF에서와 같이 볼륨 렌더링을 위한 수치 적분을 따른다.

\[\begin{equation} \alpha = 1 - \exp \left( - \frac{l}{K} \sum_{k=1}^K \textrm{explin} (\textrm{interp} (\textbf{v}_\textrm{geo}, \textbf{q}_k)) \right) \end{equation}\]

($l$은 세그먼트 길이, \(\textbf{q}_k\)는 로컬 voxel 좌표, $\textrm{interp}(\cdot)$는 trilinear interpolation)

Voxel 색상

뷰에 따른 외형을 모델링하기 위해 \(N_\textrm{shd}\) degree의 SH를 사용한다. 효율성을 높이기 위해 SH 계수 \(\textbf{v}_\textrm{sh} \in \mathbb{R}^{(N_\textrm{shd} + 1)^2 \times 3}\)가 voxel 내부에서 일정하게 유지된다고 가정한다. 효율성을 위해 3DGS를 따라 개별 광선 방향 \(\textbf{r}_d\) 대신 카메라 위치 \(\textbf{r}_o\)에서 voxel 중심 \(\textbf{v}_c\)까지의 방향에 따라 voxel 색상을 근사한다.

\[\begin{equation} c = \max (0, \textrm{sh_eval} (\textbf{v}_\textrm{sh}, \textrm{normalize} (\textbf{v}_c - \textbf{r}_o))) \end{equation}\]

근사화로 인해 voxel의 SH 색상은 voxel에 해당하는 이미지의 모든 픽셀에서 공유될 수 있다.

Voxel normal

다른 feature나 속성의 렌더링은 색상 $c$를 normal과 같은 타겟 모달리티로 대체하여 렌더링하는 것과 유사하다. 렌더링 효율성을 위해 normal이 voxel 내부에서 일정하게 유지된다고 가정한다. 이는 voxel 중심에서 density field의 analytical gradient로 표현된다.

\[\begin{equation} \textbf{n} = \textrm{normalize} (\nabla_\textbf{q} \textrm{interp} (\textbf{v}_\textrm{geo}, \textbf{q}_c)), \quad \textrm{where} \; \textbf{q}_c = (0.5, 0.5, 0,5) \end{equation}\]

SH 색상과 유사하게, 미분 가능한 voxel normal은 전처리에서 한 번 계산되고 해당하는 이미지의 모든 픽셀에서 공유된다.

Voxel 깊이

색상, normal과 달리 깊이는 계산이 효율적이므로, 볼륨 렌더링을 위한 수치 적분에서와 같이 $K$개의 포인트를 샘플링하여 더 정확한 깊이 렌더링을 수행한다.

Rasterization Algorithm

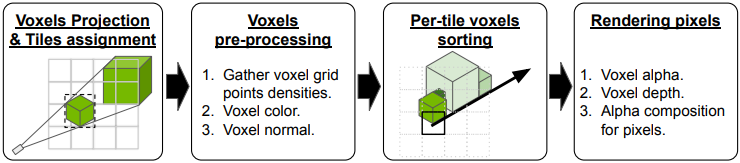
이미지 공간으로 projection

Rasterization의 첫 번째 단계는 sparse voxel을 이미지 공간에 projection하고 voxel을 덮는 타일(즉, 이미지 패치)에 할당하는 것이다. 실제로는 각 voxel의 8개 모서리 점을 projection한다. Voxel은 projection된 8개 점으로 형성된 axis-aligned bounding box (AABB)와 겹치는 모든 타일에 할당된다.

Voxel 전처리

대상 뷰의 타일에 할당된 활성 voxel의 경우, 그리드 포인트들에서 density \(\textbf{v}_\textrm{geo}\)를 수집하고, 앞서 설명한 방식으로 뷰에 따른 색상과 normal을 도출한다. 전처리된 voxel 속성은 렌더링하는 동안 모든 픽셀에서 공유된다.

Voxel 정렬


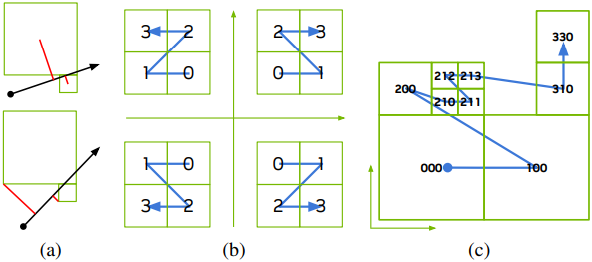
정확한 rasterization을 위해 렌더링 순서가 중요하다. (a)는 단순한 정렬 기준을 사용하였을 때 발생하는 잘못된 순서를 보여준다. Octree layout 덕분에 sparse voxel 표현을 사용하여 Morton order로 정렬할 수 있다.

(b)에서 볼 수 있듯이, 특정 유형의 Morton order를 따라 voxel을 렌더링하면 올바른 순서로 렌더링 할 수 있다. 따라야 할 Morton order의 유형은 광선 방향의 부호에만 따라 달라지며, 광선 원점은 중요하지 않다. 즉, 3D 공간에서 서로 다른 광선 방향에 대해 8가지 Morton order 순열이 있다. 3개의 레벨에 대한 2D 예시가 (c)에 나와 있다.

정렬은 각 이미지 타일에 적용된다. 타일의 모든 픽셀이 동일한 광선 방향 부호를 공유하는 경우, 할당된 voxel을 Morton order 유형에 따라 간단히 정렬할 수 있다. 여러 Morton order가 필요한 경우 코너 케이스를 처리한다.

픽셀 렌더링

마지막으로, 픽셀을 렌더링하기 위해 알파 블렌딩을 진행한다. 각 픽셀의 알파 블렌딩은 각 픽셀이 속한 타일에 할당된 sparse voxel의 수에 따라 달라진다. 픽셀 광선에 대한 sparse voxel을 렌더링할 때, 샘플링할 광선 세그먼트를 결정하기 위해 광선과 AABB 사이의 교차점을 계산하고 교차되지 않은 sparse voxel을 건너뛴다. Sparse voxel의 투과율이 임계값 $T_i < h_T$ 아래이면 알파 블렌딩을 조기에 종료한다.

안티 앨리어싱

앨리어싱 아티팩트를 완화하기 위해 \(h_\textrm{ss}\)배 더 높은 해상도로 렌더링한 후 앤티앨리어싱 필터를 사용하여 대상 해상도로 이미지를 다운샘플링한다.

2. Progressive Sparse Voxels Optimization

Voxel max sampling rate

먼저, 학습 이미지에서 각 voxel의 최대 샘플링 레이트 \(\textbf{v}_\textrm{rate}\)를 정의한다. 이는 voxel이 커버할 수 있는 이미지 영역을 반영한다. \(\textbf{v}_\textrm{rate}\)가 작을수록 voxel에 대한 관찰이 적어 overfitting될 가능성이 높아진다. 따라서 \(\textbf{v}_\textrm{rate}\)를 voxel 초기화와 voxel subdivision 프로세스에서 \(\textbf{v}_\textrm{rate}\)를 사용한다.


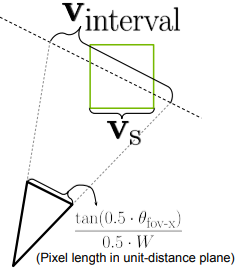
\(N_\textrm{cam}\)개의 학습 카메라가 주어지면, 다음과 같이 voxel의 최대 샘플링 레이트를 추정한다.

\[\begin{aligned} \textbf{v}_\textrm{rate} &= \max_i^{N_\textrm{cam}} \frac{\textbf{v}_s}{\textbf{v}_\textrm{interval}^{(i)}} \\ \textbf{v}_\textrm{interval}^{(i)} &= \underbrace{(\textbf{v}_c - \textbf{r}_o^{(i)})^\top \ell^{(i)}}_{\textrm{Voxel z-distance}} \cdot \underbrace{\frac{\tan (0.5 \cdot \theta_\textrm{fov-x}^{(i)})}{0.5 \cdot W^{(i)}}}_{\textrm{Unit-distance pixel size}} \end{aligned}\]

($\ell$은 카메라 lookat 벡터, \(\theta_\textrm{fov-x}\)는 카메라 수평 FOV, $W$는 이미지 너비)

샘플링 레이트는 voxel에 충돌할 수 있는 이미지의 수평 축 방향을 따라 추정된 광선 수를 나타낸다.

Scene Initialization

추가적인 prior를 사용하지 않고 모든 파라미터를 상수로 초기화한다. Volume density가 0에 가까워지도록 초기화하기 위해 voxel density를 음수인 \(h_\textrm{geo}\)로 설정하여 초기 density가 \(\textrm{explin}(h_\textrm{geo}) \approx 0\)이 되도록 한다.

SH 계수의 경우, degree가 0인 계수는 0.5로 (회색), 나머지는 0으로 설정한다.

Bounded scenes

재구성할 장면이나 물체가 알려진 경계 영역에 둘러싸여 있는 경우, \(h_\textrm{lv}\)개의 레벨이 있는 그리드로 레이아웃을 초기화하고 어떠한 학습 이미지에서도 관찰되지 않은 voxel을 제거한다. 초기화 후 voxel 수는 \((2^{h_\textrm{lv}})^3\)보다 적다.

Unbounded scenes


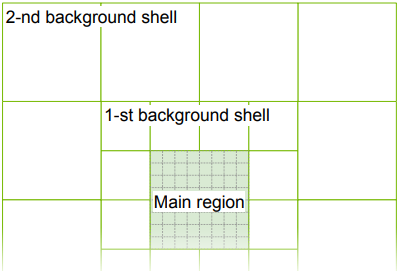
Unbounded scene의 경우, 먼저 공간을 위 그림에서와 같이 메인 영역과 배경 영역으로 분할한다. 각 영역은 서로 다른 휴리스틱을 사용한다. 학습 카메라 위치를 사용하여 메인 영역에 해당하는 직육면체를 결정한다. 직육면체의 중심은 평균 카메라 위치로 설정되고 반경은 직육면체 중심과 카메라 사이의 중간 거리로 설정된다. 메인 영역은 bounded scene과 마찬가지로 \(h_\textrm{lv}\)개의 레벨이 있는 그리드로 초기화된다.

배경 영역의 경우 메인 영역을 둘러싸는 \(h_\textrm{out}\)개의 레벨로 구성된 배경 셸을 할당한다. 즉, 전체 장면의 반경은 메인 영역의 \(2^{h_\textrm{out}}\)배이다. 각 배경 셸 레벨은 가장 coarse한 voxel 크기, 즉 $4^3 - 2^3 = 56$개의 voxel로 시작한다. 그런 다음 가장 높은 샘플링 레이트로 셸 voxel을 반복적으로 subdivision하고 어떤 학습 카메라에서도 관찰되지 않은 voxel을 제거한다. 배경 영역과 메인 영역의 voxel 수의 비율이 \(h_\textrm{ratio}\)가 될 때까지 프로세스가 반복된다. 초기화 후 voxel 수는 \((1 + h_\textrm{ratio})(2^{h_\textrm{lv}})^3\)보다 적다.

Adaptive Pruning and Subdivision

초기화된 그리드 레이아웃은 학습 진행 중에 장면의 다양한 level of detail에 적응적으로 정렬되어야 하는 전체 장면을 대략적으로만 포함한다. 이 목적을 달성하기 위해 모든 학습 반복마다 pruning과 subdivision를 적용한다.

Pruning

모든 학습 카메라를 사용하여 각 voxel의 최대 블렌딩 가중치 \(T_i \alpha_i\)를 계산한다. 그런 다음, \(h_\textrm{prune}\)보다 낮은 최대 블렌딩 가중치를 가진 voxel을 제거한다.

Subdivision

학습 loss의 gradient가 더 큰 voxel은 voxel 영역이 더 미세한 voxel을 필요로 한다는 것을 나타낸다. 구체적으로, 다음과 같이 subdivision 우선순위를 누적한다.

\[\begin{equation} \textbf{v}_\textrm{priority} = \sum_{\textbf{r} \in R} \| \alpha (\textbf{r}) \cdot \frac{\partial \mathcal{L} (\textbf{r})}{\partial \alpha (\textbf{r})} \| \end{equation}\]

($R$은 모든 학습 픽셀 광선의 집합, $\mathcal{L}(\textbf{r})$은 광선의 학습 loss)

Gradient는 voxel에서 광선으로 기여한 alpha 값으로 가중된다. \(\textbf{v}_\textrm{priority}\)가 높을수록 subdivision 우선순위가 높다. Voxel이 몇몇 픽셀에 overfitting되는 것을 방지하기 위해 샘플링 레이트 threshold \(2h_\textrm{rate}\)보다 낮은 최대 샘플링 레이트 \(\textbf{v}_\textrm{rate}\)를 가진 voxel에 대한 우선순위를 0으로 설정한다.

마지막으로, subdivision할 상위 \(h_\textrm{percent}\) 퍼센트의 높은 우선순위를 가지는 voxel을 선택한다. 즉, voxel의 총 수는 \(7 h_\textrm{percent}\) 퍼센트만큼 증가한다. Octree layout에서는 리프 노드만 유지하므로 subdivision되면 원래 voxel을 제거한다.

Voxel을 pruning하고 subdivision할 때 voxel SH 계수와 격자점 density를 그에 따라 업데이트해야 한다. SH 계수는 간단하게 voxel과 동일하게 pruning되고 subdivision된 자식 voxel에 복제된다. 격자점 density는 8개의 voxel 모서리 격자점이 인접한 voxel 간에 공유되므로 약간 더 복잡하다. Pruning의 경우, 어떤 voxel 모서리에도 속하지 않을 때만 격자점을 제거한다. Subdivision의 경우, trilinear interpolation을 사용하여 새로운 격자점의 density를 계산하고, 복제된 격자점은 병합되고 density는 평균화된다.

Optimization objectives

렌더링된 이미지와 실제 이미지 사이의 photometric loss로 MSE와 SSIM을 사용한다. 전반적인 학습 loss는 다음과 같다.

\[\begin{aligned} \mathcal{L} = \,& \mathcal{L}_\textrm{mse} + \lambda_\textrm{ssim} \mathcal{L}_\textrm{ssim} \\ &+ \lambda_\textrm{T} \mathcal{L}_\textrm{T} + \lambda_\textrm{dist} \mathcal{L}_\textrm{dist} + \lambda_\textrm{R} \mathcal{L}_\textrm{R} + \lambda_\textrm{tv} \mathcal{L}_\textrm{tv} \end{aligned}\]
  • \(\mathcal{L}_\textrm{T}\): 최종 광선 투과율이 0 또는 1이 되도록 장려
  • \(\mathcal{L}_\textrm{dist}\): Mip-NeRF 360의 distortion loss
  • \(\mathcal{L}_\textrm{R}\)은 DVGO의 per-point rgb loss
  • \(\mathcal{L}_\textrm{tv}\): sparse density grid의 total variation loss

메쉬 추출 task에서는 2DGS의 depth-normal consistency loss도 추가한다.

\[\begin{equation} \mathcal{L}_\textrm{mesh} = \lambda_\textrm{n-dmean} \mathcal{L}_\textrm{n-dmean} + \lambda_\textrm{n-dmed} \mathcal{L}_\textrm{n-dmed} \end{equation}\]

두 loss 모두 평균 및 중앙값 깊이에서 렌더링된 normal과 깊이에서 계산된 normal 간의 정렬을 촉진한다.

Sparse-voxel TSDF Fusion and Marching Cubes

Sparse voxel은 그리드 기반 알고리즘과 완벽하게 통합될 수 있다. 메쉬를 추출하기 위해 Marching Cubes를 구현하여 sparse voxel에서 density에 대한 등위면(isosurface)의 삼각형을 추출한다. 인접한 voxel에서 복제된 vertex들은 병합되어 고유한 vertex 집합을 생성한다. 인접한 voxel이 다른 Octree 레벨에 속할 때, density field가 다른 레벨의 voxel에 대해 연속적이지 않기 때문에 추출된 삼각형이 연결되지 않을 수 있다. 이러한 불연속성은 모든 voxel을 가장 미세한 레벨로 subdivision하여 제거할 수 있다.

Density field에서 등위면을 추출하기 위한 타겟 level set을 결정하는 것은 까다로울 수 있다. 대신, sparse-voxel TSDF-Fusion을 구현하여 sparse 그리드 포인트의 TSDF 값을 계산한다. 그런 다음, sparse-voxel Marching Cubes를 사용하여 zero-level set의 표면을 직접 추출할 수 있다.

Experiments

  • 구현 디테일
    • $h_\textrm{geo} = -10$
    • $h_\textrm{lv} = 6$
    • $h_\textrm{out} = 5$, $h_\textrm{ratio} = 2$
    • $h_\textrm{T} = 1 \times 10^{-4}$, $h_\textrm{ss} = 1.5$
    • $K$: novel view synthesis는 1, mesh reconstruction은 3
    • $h_\textrm{every} = 1,000$
    • $h_\textrm{prune}$: 0.0001에서 0.05로 선형적으로 증가
    • $h_\textrm{percent} = 5$

1. Novel-view Synthesis

다음은 MipNeRF-360 데이터셋에서 novel view synthesis를 비교한 결과이다.


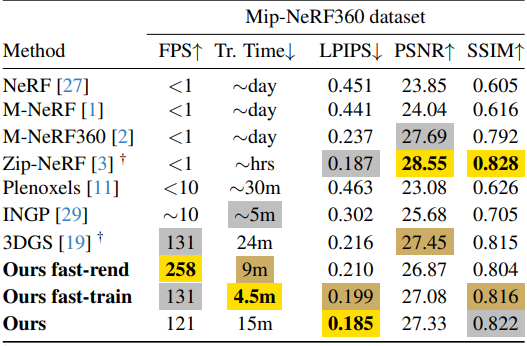
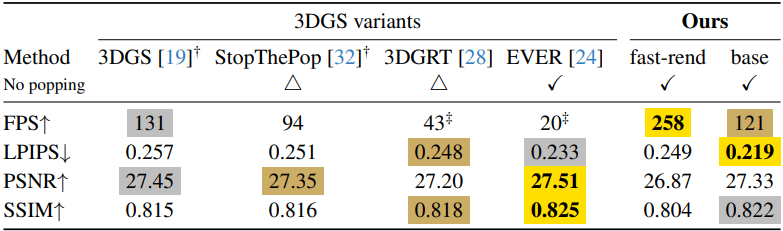
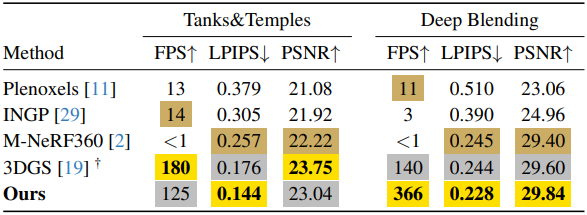
다음은 Tanks&Temples와 Deep Blending에서 novel view synthesis를 비교한 표이다.


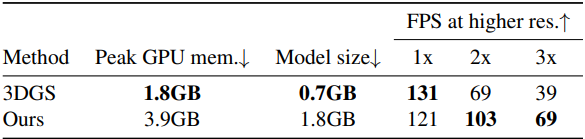
다음은 MipNeRF-360 데이터셋에서 GPU 메모리, 모델 크기, 더 높은 해상도에서의 FPS를 3DGS와 비교한 표이다.

2. Ablation Studies

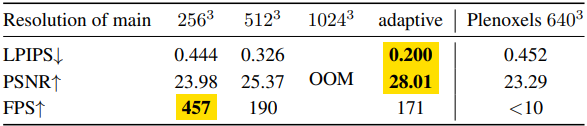
다음은 메인 영역의 voxel 크기에 대한 ablation 결과이다.

3. Mesh Reconstruction

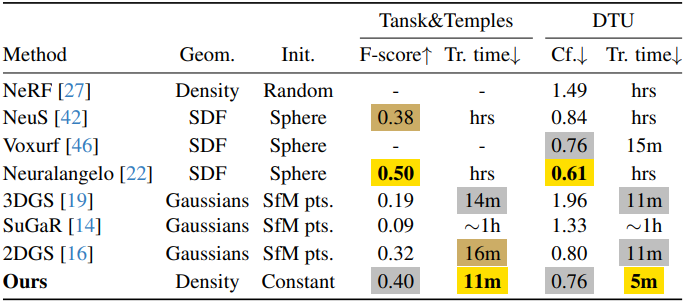
다음은 Tanks&Temples와 DTU 데이터셋에서 메쉬 재구성을 비교한 결과이다.

Limitation


학습 뷰의 노출 변화가 심한 장면의 경우, 서로 다른 밝기의 명확한 경계를 생성하고 많은 floater를 할당한다. 3DGS는 GT의 이러한 변화에 덜 민감하다.

You may also enjoy