[논문리뷰] SuGaR: Surface-Aligned Gaussian Splatting for Efficient 3D Mesh Reconstruction and High-Quality Mesh Rendering

CVPR 2024. [Paper] [Page] [Github]
Antoine Guédon, Vincent Lepetit
LIGM | Ecole des Ponts | Univ Gustave Eiffel | CNRS
21 Nov 2023

Introduction

최근 3D Gaussian Splatting은 3D 장면을 캡처하고 새로운 뷰에서 렌더링하는 데 매우 인기가 있다. 3D Gaussian Splatting은 장면의 형상과 외형을 캡처하기 위해 장면의 학습 이미지셋을 기반으로 많은 3D Gaussian들의 위치, 방향, 외형(spherical harmonics로 표현), alpha blendin을 최적화한다. Gaussian 렌더링은 neural field 렌더링보다 훨씬 빠르기 때문에 3D Gaussian Splatting은 NeRF보다 훨씬 빠르며 몇 분 안에 장면을 캡처할 수 있다.

Gaussian은 장면의 매우 사실적인 렌더링을 가능하게 하지만 장면의 표면을 추출하는 것은 여전히 어렵다. 3D Gaussian Splatting으로 최적화한 후 Gaussian들은 일반적으로 정렬된 구조를 취하지 않으며 장면의 실제 표면과 잘 일치하지 않는다. 메쉬는 많은 파이프라인에서 선택적으로 사용되는 표현이기 때문에 장면을 메쉬로 표현하는 것이 바람직한 경우가 많다. 메쉬 기반 표현을 사용하면 편집, 조각, animating, relighting 등을 위한 강력한 도구를 사용할 수 있다. Gaussian Splatting 이후의 Gaussian은 구조화되지 않았기 때문에 여기서 메쉬를 추출하는 것은 매우 어렵다. 비록 다른 이유가 있기는 하지만 이는 NeRF에서도 어려운 일이다.

본 논문에서는 Gaussian들이 표면에 잘 분산되어 형상을 훨씬 더 잘 포착할 수 있도록 하는 정규화 항을 제안하였다. 본 논문의 접근 방식은 Gaussian들이 평평하고 표면에 잘 분포되어 있다는 가정하에 Gaussian에서 볼륨 밀도를 도출하는 것이다. 이 밀도와 최적화 중에 Gaussian에서 계산된 실제 밀도 사이의 차이를 최소화함으로써 3D Gaussian들이 형상을 잘 표현하도록 권장한다.

이 정규화 항 덕분에 Gaussian에서 메쉬를 추출하는 것이 더 쉬워졌다. 실제로 정규화 항을 평가하기 위해 밀도 함수를 도입했기 때문에 자연스러운 접근 방식은 이 밀도 함수의 level set을 추출하는 것이다. 그러나 Gaussian Splatting은 장면의 디테일을 높은 정확도로 캡처하기 위해 densification을 수행하므로 Gaussian 수가 급격히 증가한다. 실제 장면은 일반적으로 크기와 회전이 서로 다른 수백만 개의 3D Gaussian들로 구성되며, 그 중 대부분은 장면의 텍스처와 디테일을 재현하기 위해 매우 작다. 이로 인해 거의 모든 곳에서 0에 가까운 밀도 함수가 생기며 Marching Cubes 알고리즘은 미세한 복셀 그리드에서도 이러한 sparse한 밀도 함수의 적절한 level set들을 추출하지 못한다.

대신에 밀도 함수의 level set의 보이는 부분에서 포인트를 매우 효율적으로 샘플링하는 방법을 도입하여 이러한 포인트에서 Poisson reconstruction 알고리즘을 실행하여 삼각형 메쉬를 얻을 수 있다. Marching Cubes 알고리즘과 달리 이 접근 방식은 확장 가능하며, 여러 GPU에서 24시간이 걸리는 nerual SDF를 사용하는 다른 SOTA 방법과 달리 단일 GPU에서 몇 분 내에 표면 메쉬를 재구성한다.

본 논문의 방법은 고품질 메쉬를 생성한다. 문제는 level set에 있는 포인트를 효율적으로 식별하는 것이다. 이를 위해 학습 뷰에서 본 Gaussian depth map을 사용한다. 이 depth map은 Gaussian Splatting rasterizer를 확장하여 얻을 수 있으며 이 depth map에서 시작하여 level set의 포인트를 정확하게 샘플링한다.

마지막으로, 저자들은 이 메쉬를 추출한 후 Gaussian Splatting 렌더링만을 통해 메쉬와 3D Gaussian 집합을 공동으로 최적화하는 선택적 개선 전략을 제안하였다. 이러한 최적화를 통해 기존 텍스처 메쉬 렌더링 대신 Gaussian Splatting 렌더링을 사용하여 메쉬의 고품질 렌더링이 가능해졌다. 이는 inference 시 기본 메쉬에 의존하는 다른 radiance field 모델보다 렌더링 품질 측면에서 더 높은 성능을 제공한다. 이를 통해 장면의 Gaussian Splatting 표현을 편집하기 위한 전통적인 메쉬 편집 도구를 사용할 수 있어 컴퓨터 그래픽에 대한 무한한 가능성을 제공한다.

Method

1. Aligning the Gaussians with the Surface

Gaussian에서 메쉬 생성을 용이하게 하기 위해 Gaussian이 표면에 정렬되고 이 표면에 잘 분산되도록 하는 정규화 항을 Gaussian Splatting 최적화에 도입한다. 본 논문의 접근 방식은 Gaussian들이 원하는 속성을 가지고 있다는 가정하에 Gaussian으로부터 SDF를 도출하는 것이다. 이 SDF와 Gaussian에 대해 계산된 실제 SDF 간의 차이를 최소화함으로써 Gaussian이 이러한 속성을 갖도록 장려한다.

주어진 Gaussian Splatting 장면에 대해 해당 밀도 함수 $d: \mathbb{R}^3 \rightarrow \mathbb{R}^{+}$를 고려하는 것부터 시작한다. 이는 임의의 공간 위치 $p$에서 alpha-blending 계수로 가중된 Gaussian 값의 합으로 계산된다.

\[\begin{equation} d(p) = \sum_g \alpha_g \exp \bigg( -\frac{1}{2} (p - \mu_g)^\top \Sigma_g^{-1} (p - \mu_g) \bigg) \end{equation}\]

여기서 $\mu_g$, $\Sigma_g$, $\alpha_g$는 각각 Gaussian의 중심, 공분산, alpha-blending 계수이다. Gaussian이 잘 분포되고 표면과 정렬되면 이 밀도 함수가 어떻게 되는지 생각해 보자.

먼저, 이러한 시나리오에서 Gaussian은 이웃과 겹치는 것이 제한적이다. 표면에 가까운 임의의 점 $p \in \mathbb{R}^3$에 대해 점 $p$에 가장 가까운 Gaussian $g^\ast$는 밀도 값 $d(p)$에 다른 것보다 훨씬 더 많이 기여할 가능성이 높다. 그러면 $p$에서 Gaussian 밀도를 다음과 같이 근사화할 수 있다.

\[\begin{equation} \alpha_{g^\ast} \exp \bigg( -\frac{1}{2} (p - \mu_{g^\ast})^\top \Sigma_{g^\ast}^{-1} (p - \mu_{g^\ast}) \bigg) \end{equation}\]

여기서 가장 가까운 Gaussian $g^\ast$는 $p$에서 가장 큰 기여를 하는 Gaussian으로 간주된다.

\[\begin{equation} g^\ast = \underset{g}{\arg \min} \{ (p - \mu_g)^\top \Sigma_g^{-1} (p - \mu_g) \} \end{equation}\]

따라서 $p$에서의 Gaussian 밀도 식은 밀도에 가장 가까운 Gaussian $g^\ast$의 기여도가 다른 Gaussian의 기여도보다 훨씬 높다는 것을 고려한다. 이는 Gaussian이 잘 확산되도록 장려하는 데 도움이 될 것이다.

또한 3D Gaussian이 메쉬 표면과 더 가깝게 정렬되므로 평평해져야 한다. 결과적으로, 모든 Gaussian $g$는 세 가지 scaling factor 중 하나가 0에 가까워야하며 다음과 같다.

\[\begin{equation} (p - \mu_g)^\top \Sigma_g^{-1} (p - \mu_g) \approx \frac{1}{s_g^2} \langle p - \mu_g, n_g \rangle^2 \end{equation}\]

여기서 $s_g$는 Gaussian의 가장 작은 scaling factor이고 $n_g$는 해당 축의 방향이다. 게다가 Gaussian이 장면의 실제 표면을 묘사하여야 하기 때문에 반투명한 Gaussian을 피해야 한다. 따라서 Gaussian이 불투명하거나 완전히 투명해야 하며, 이 경우 렌더링을 위해 Gaussian을 삭제할 수 있다. 결과적으로 모든 Gaussian $g$에 대해 $\alpha_g = 1$이어야 한다.

이러한 시나리오에서 Gaussian의 밀도는 최종적으로 다음과 같이 밀도 $\bar{d}(p)$로 근사화될 수 있다.

\[\begin{equation} \bar{d} (p) = \exp \bigg( - \frac{1}{2 s_{g^\ast}^2} \langle p - \mu_{g^\ast}, n_{g^\ast} \rangle^2 \bigg) \end{equation}\]

정규화를 위한 첫 번째 전략은 $\vert d(p) − \bar{d}(p) \vert$ 항을 최적화 loss에 추가하는 것이다. 이 접근 방식은 Gaussian을 표면에 정렬하는 데 효과적이지만, 저자들은 밀도가 아닌 SDF에 의존하여 약간 다른 loss를 계산하면 표면에 대한 Gaussian 정렬이 더욱 잘 된다는 것을 발견했다. 주어진 평평한 Gaussian ($s_g = 0$)에 대하여 모든 level set이 법선 $n_g$를 사용하여 Gaussian의 중심 $\mu_g$를 통과하는 평면을 향해 degenerate되기 때문에 level set을 고려하는 것은 의미가 없다. 포인트 $p$와 장면의 실제 표면 사이의 거리는 대략 $\vert \langle p − \mu_g, n_g \rangle \vert$이다. 결과적으로, SDF의 zero-crossing

\[\begin{equation} \bar{f}(p) = \pm s_{g^\ast} \sqrt{-2 \log (\bar{d} (p))} \end{equation}\]

은 장면의 표면에 해당한다. 보다 일반적으로 밀도 함수와 관련된 이상적인 거리 함수 $d$를 다음과 같이 정의한다.

\[\begin{equation} f(p) = \pm s_{g^\ast} \sqrt{-2 \log (d(p))} \end{equation}\]

이 거리 함수는 $d = \bar{d}$인 이상적인 시나리오에서 장면의 실제 표면에 해당한다. 따라서 정규화 항 $\mathcal{R}$을 다음과 같다.

\[\begin{equation} \mathcal{R} = \frac{1}{\mathcal{P}} \sum_{p \in \mathcal{P}} \vert \hat{f} (p) - f(p) \vert \end{equation}\]

3D 포인트 $p$를 샘플링하고 이러한 포인트들에서의 이상적인 SDF $f(p)$와 현재 Gaussian에 의해 생성된 표면 SDF의 추정치 $f(p)$ 사이의 차이를 합산한다. $\mathcal{P}$는 샘플링된 포인트 집합이다.

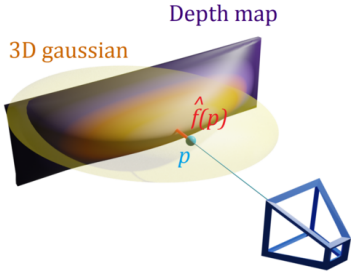
$\hat{f}(p)$를 효율적으로 계산하는 것은 어려운 일이다. 이를 위해 학습에 사용되는 뷰에서 Gaussian의 depth map을 사용한다. 이러한 depth map은 Gaussian Splatting rasterizer를 확장하여 효율적으로 렌더링할 수 있다. 그러면 위 그림에서 볼 수 있듯이 학습 뷰에서 보이는 포인트 $p$에 대해 이상적인 SDF $f(p)$는 $p$의 깊이와 $p$의 projection에서 해당 depth map의 깊이 사이의 차이다. 또한 Gaussian 분포에 따라 점 $p$를 샘플링한다.

\[\begin{equation} p \sim \prod_g \mathcal{N} (\cdot; \mu_g, \Sigma_g) \end{equation}\]

평균이 $\mu_g$이고 공분산이 $\Sigma_g$인 Gaussian 분포 $\mathcal{N} (\cdot; \mu_g, \Sigma_g)$을 사용하면 샘플링된 $p$들이 $\mathcal{R}$에 대한 높은 기울기에 해당할 가능성이 높기 때문이다.

또한 SDF $f$의 법선과 SDF $\bar{f}$의 법선이 비슷하도록 장려하기 위해 정규화 항을 추가한다.

\[\begin{equation} \mathcal{R}_\textrm{Norm} = \frac{1}{\mathcal{P}} \sum_{p \in \mathcal{P}} \bigg\| \frac{\nabla f(p)}{\| \nabla f(p) \|_2} - n_{g^\ast} \bigg\|_2^2 \end{equation}\]

2. Efficient Mesh Extraction

두 정규화 항을 사용한 최적화 후 얻은 Gaussian들로부터 메쉬를 생성하기 위해 Gaussian에서 계산된 밀도 level set에서 3D 포인트를 샘플링한다. Level set은 level parameter $\lambda$에 따라 달라진다. 그런 다음 이 포인트에서 간단히 Poisson reconstruction을 실행하여 메쉬를 얻는다. 또한 SDF의 법선을 사용하여 점을 쉽게 할당할 수 있으므로 메쉬 품질이 향상된다.

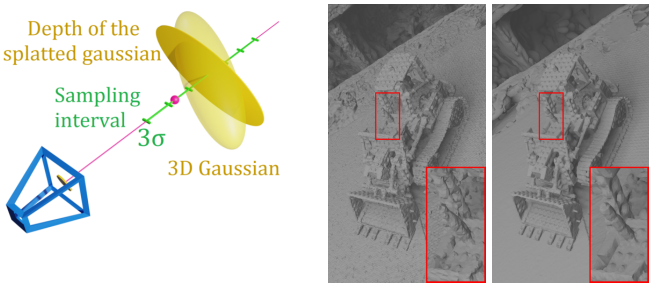
문제는 level set에 있는 포인트를 효율적으로 식별하는 것이다. 이를 위해 위 그림에서 볼 수 있듯이 학습 뷰에서 볼 수 있는 Gaussian depth map에 다시 의존한다. 먼저 각 depth map에서 무작위로 픽셀을 샘플링한다. 각 픽셀 $m$에 대해 광선을 샘플링하여 level set에서 3D 포인트를 찾는다.

$n$개의 포인트 $p + t_i v$를 샘플링한다. 여기서 $p$는 픽셀 $m$에 재투영되는 depth map의 3D 포인트이고, $v$는 광선의 방향이며, $t_i \in [-3 \sigma_g (v), 3 \sigma_g (v)]$이다. 여기서 $\sigma_g (v)$는 카메라 방향의 3D Gaussian $g$의 표준 편차이다. $[-3 \sigma_g (v), 3 \sigma_g (v)]$은 광선의 $t$에 대한 1D Gaussian 함수의 99.7 신뢰 수준에 대한 신뢰 구간이다.

그런 다음 샘플링된 점들의 밀도 값 $d_i = d(p + t_i v)$를 계산한다. $d_i < \lambda < d_j$인 $i$, $j$가 존재하는 경우 이 범위에 level set 포인트가 있다. 그렇다면 linear interpolation을 사용하여 $p + t^\ast v$가 카메라에 가장 가까운 level set 포인트가 되도록 $t^\ast$를 계산하고 $d(p + t^\ast v) = λ$를 확인한다. 또한 포인트 $\hat{p}$에서 표면의 법선을 밀도의 정규화된 기울기로 계산한다.

\[\begin{equation} \frac{\nabla d (\hat{p})}{\| \nabla d (\hat{p}) \|_2} \end{equation}\]

마지막으로, level set 포인트들과 해당 법선으로부터 표면 메쉬를 재구성하기 위해 Poisson reconstruction을 적용한다.

3. Binding New 3D Gaussians to the Mesh

첫 번째 메쉬를 추출한 후에는 새 Gaussian을 메쉬 삼각형에 바인딩하여 이 메쉬를 개선하고 Gaussian Splatting rasterizer를 사용하여 Gaussian과 메쉬를 공동으로 최적화할 수 있다. 이를 통해 Gaussian 덕분에 고품질 렌더링을 유지하면서 널리 사용되는 메쉬 편집 도구를 사용하여 Gaussian Splatting 장면을 편집할 수 있다.

초기 메쉬가 주어지면 메쉬에 새로운 3D Gaussian를 instantiate한다. 보다 정확하게는 아래 그림과 같이 삼각형의 표면에서 샘플링된 $n$개의 얇은 3D Gaussian 집합을 메쉬의 각 삼각형에 연관시킨다. 이를 위해 원래 3D Gaussian Splatting 모델의 구조를 약간 수정한다.

최적화 중에 해당 삼각형에 미리 정의된 무게 중심 좌표를 사용하여 메쉬 정점에서 Gaussian 평균을 명시적으로 계산한다. 또한 Gaussian에는 3개가 아닌 2개의 학습 가능한 scaling factor와 복소수로 인코딩된 1개의 학습 가능한 2D rotation만 있어 Gaussian을 평평하게 유지하고 메쉬 삼각형과 정렬된다. 원본 모델과 마찬가지로 모든 Gaussian에 대한 불투명도 값과 spherical harmonics 집합을 최적화하여 모든 방향으로 방출되는 색상을 인코딩한다.

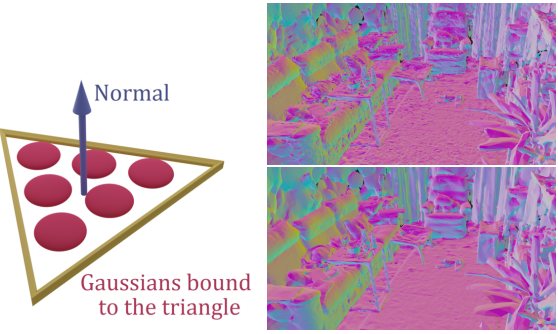
위 그림은 미세 조정 전과 후의 메쉬의 예를 보여준다.

Experiments

• 구현 디테일
  • GPU: Nvidia Tesla V100 SXM2 32B 1개
  • Regularization
    • 처음 7,000 iteration에는 Gaussian들이 제약조건을 가지지 않도록 정규화를 사용하지 않음
    • 그런 다음 2,000 iteration동안 불투명도 $\alpha_g$에 대한 추가 entropy loss를 적용
    • 불투명도가 0.5보다 작은 Gaussian들을 제거 후 정규화 항을 추가하여 6,000 iteration 수행
    • 밀도 계산 시 16개의 가까운 Gaussian들만 계산하고 500 iteration마다 nearest neighbors를 업데이트
    • 일반적으로 15분에서 45분 소요
  • Mesh extraction
    • $\lambda = 0.3$
    • Poisson reconstruction: depth 10, quadric error metrics
    • 일반적으로 5분에서 10분 소요
  • Joint refinement
    • iteration: 2,000 / 7,000 / 15,000
    • iteration 수에 따라 몇 분에서 1시간 소요

1. Real-Time Rendering of Real Scenes

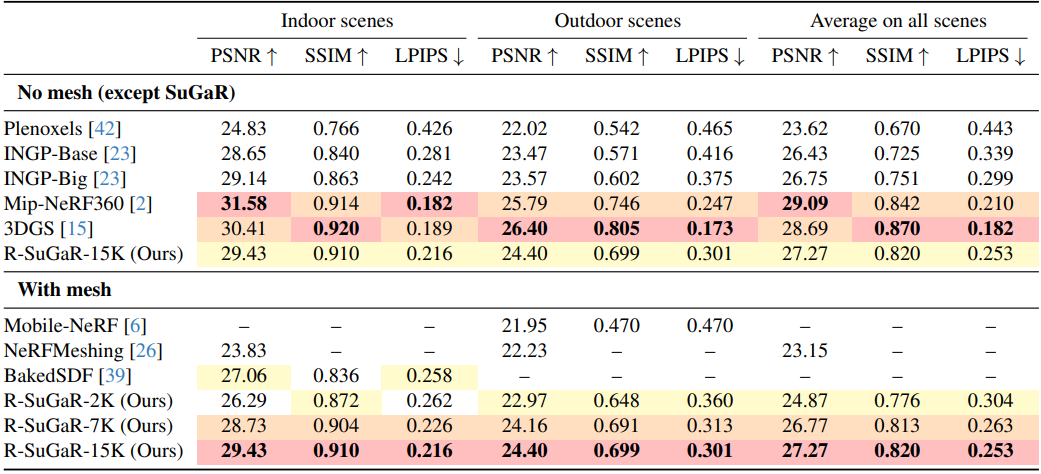
다음은 Mip-NeRF360 데이터셋에 대한 렌더링 품질을 비교한 표이다.

다음은 SuGaR의 렌더링 결과(a)와 재구성된 메쉬들(b)이다.

2. Mesh Extraction

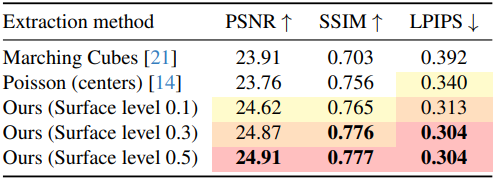
다음은 메쉬 추출 방법에 대한 ablation 결과이다. (Mip-NeRF360)

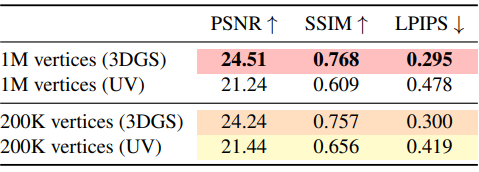
3. Mesh Rendering Ablation

다음은 표면이 정렬된 3D Gaussian들과 최적화된 전통적인 UV 텍스처를 비교한 표이다. (Mip-NeRF360)