[논문리뷰] Revisiting Stereo Depth Estimation From a Sequence-to-Sequence Perspective with Transformers (STTR)

ICCV 2021 (Oral). [Paper] [Github]
Zhaoshuo Li, Xingtong Liu, Nathan Drenkow, Andy Ding, Francis X. Creighton, Russell H. Taylor, Mathias Unberath
Johns Hopkins University
5 Nov 2020

Introduction

Stereo depth estimation은 3D 정보를 재구성할 수 있기 때문에 상당한 관심을 끌고 있다. 이를 위해 왼쪽과 오른쪽 카메라 이미지 간에 해당 픽셀이 매칭된다. 해당 픽셀 위치의 차이, 즉 disparity(시차)를 사용하여 깊이를 추론하고 3D 장면을 재구성할 수 있다. Stereo depth estimation에 대한 최근 딥러닝 기반 접근 방식은 유망한 결과를 보여주었지만 몇 가지 과제가 남아 있다.

그러한 과제 중 하나는 제한된 disparity 범위를 사용하는 것과 관련이 있다. 이론적으로 disparity 값의 범위는 카메라의 해상도/baseline과 물리적 물체와의 근접성에 따라 0부터 이미지 너비까지일 수 있다. 그러나 최고의 성능을 내는 접근 방식 중 다수는 수동으로 미리 지정된 disparity 범위(일반적으로 최대 192px)로 제한된다. 이러한 방법은 여러 후보에 대해 매칭 비용이 계산되고 최종 예측된 disparity 값이 합계로 계산되는 “cost volume”에 의존한다. 이러한 자체적으로 부과된 disparity 범위는 이러한 방법의 메모리에서 맞는 구현을 위해 필요하지만 실제 장면 및 카메라 설정의 속성에는 유연하지 않다. 자율 주행이나 내시경과 같은 응용 분야에서는 충돌을 피하기 위해 카메라 설정에 관계없이 가까운 물체를 인식하는 것이 중요하므로 고정된 disparity 범위 가정을 완화할 필요가 있다.

비학습 기반 접근 방식에서 사용되는 occlusion 및 매칭 uniqueness에 대한 기하학적 특성 및 제약 조건도 학습 기반 접근 방식에서 누락되는 경우가 많다. Stereo depth estimation의 경우 가려진 영역에는 유효한 disparity가 없다. 이전 알고리즘들은 일반적으로 조각별 smoothness 가정을 통해 가려진 영역에 대한 차이를 추론하는데, 이는 항상 유효하지 않을 수 있다. Disparity 값과 함께 신뢰도 추정치를 제공하는 것은 가려지거나 신뢰도가 낮은 추정치에 가중치를 부여하거나 거부할 수 있도록 다운스트림 분석에 유리할 것이다. 그러나 대부분의 이전 접근 방식들은 그러한 정보를 제공하지 않는다. 또한 한 이미지의 픽셀은 실제 장면의 동일한 위치에 해당하므로 다른 이미지의 여러 픽셀과 일치해서는 안 된다. 이 제약 조건은 모호성을 해결하는 데 분명히 유용할 수 있지만 대부분의 기존 학습 기반 접근 방식에서는 이를 부과하지 않는다.

앞서 언급한 문제는 cost volume을 구성하려는 현대 stereo matching 관점의 단점에서 크게 발생한다. Epipolar line을 따라 sequence-to-sequence matching 관점에서 disparity 추정을 고려하는 접근 방식을 사용하면 이러한 문제를 피할 수 있다. 이러한 방법은 새로운 것이 아니며, 동적 프로그래밍을 사용한 첫 번째 시도가 1985년에 제안되었다. 여기서 epipolar line 내외의 정보는 uniqueness 제약 조건과 함께 사용된다. 그러나 픽셀 강도 간의 유사도만 매칭 기준으로 사용했는데, 이는 로컬 매칭만으로는 부족하여 성능이 제한되었다.

Feature descriptor 간의 장거리 연관성을 포착하는 attention 기반 네트워크의 최근 발전으로 인해 저자들은 이러한 관점을 재검토하게 되었다. 본 논문은 Transformer 아키텍처와 feature matching의 최근 발전을 활용하여 STereo TRansformer (STTR)라는 새로운 end-to-end로 학습된 stereo depth estimation 네트워크를 제시하였다. STTR의 주요 장점은 픽셀별 상관관계를 dense하게 계산하고 고정된 disparity의 cost volume을 구성하지 않는다는 것이다. 따라서 STTR은 성능 저하가 거의 또는 전혀 없이 위에 자세히 설명된 대부분의 최신 접근 방식의 단점을 완화할 수 있다. STTR은 합성 및 실제 이미지 벤치마크에 대하여 경쟁력 있는 성능을 보였으며 합성 이미지에 대해서만 학습된 STTR은 개선 없이 다른 도메인에도 잘 일반화된다.

The Stereo Transformer Architecture

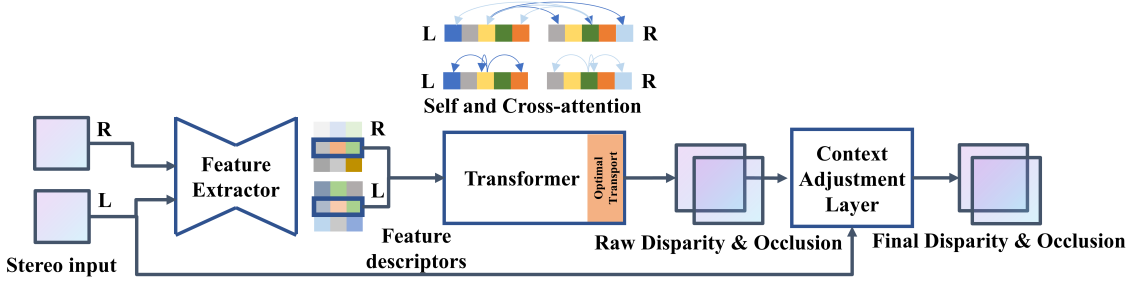
Rectify된 이미지 쌍의 높이와 너비를 각각 $I_h$와 $I_w$라 하고 feature descriptor의 채널 차원을 $C$로 나타낸다.

1. Feature Extractor

보다 효율적인 글로벌 컨텍스트 획득을 위해 residual connection과 및 spatial pyramid pooling module로 인코딩 경로가 수정된다는 점을 제외하고 Extremely Dense Point Correspondences using a Learned Feature Descriptor와 유사한 모래시계 모양의 아키텍처를 사용한다. 디코딩 경로는 transposed convolution, Dense-Blocks, 최종 convolution layer로 구성된다. 크기가 $C_e$인 각 픽셀의 feature descriptor $e_I$는 로컬 및 글로벌 컨텍스트를 모두 인코딩한다. 최종 feature map은 입력 이미지와 동일한 공간 해상도를 갖는다.

2. Transformer

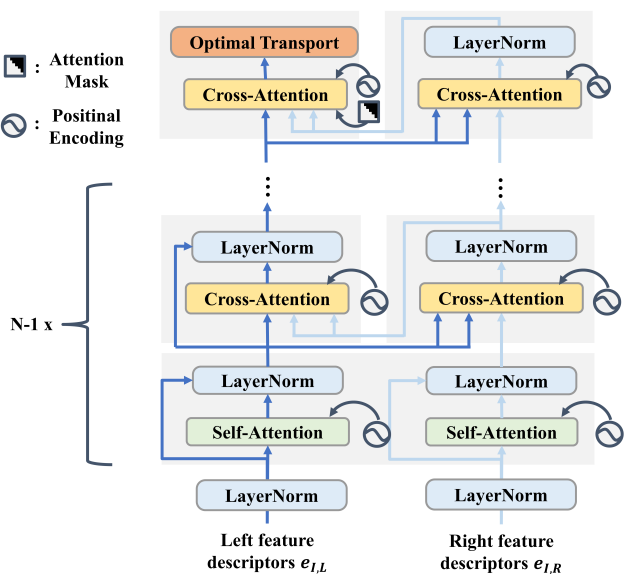
여기에 사용된 Transformer 아키텍처의 개요는 위 그림에 나와 있다. 저자들은 SuperGlue의 교대 attention 메커니즘을 채택하였다. Self-attention은 동일한 이미지에서 epipolar line을 따라 픽셀 간의 attention을 계산하는 반면, cross-attention은 왼쪽과 오른쪽 이미지의 대응되는 epipolar line을 따라 픽셀의 attention을 계산한다. 위 그림에서 볼 수 있듯이 $N - 1$개의 레이어에 대해 self-attention과 cross-attention 계산을 번갈아 가며 수행한다. 이 교대 방식은 이미지 컨텍스트와 상대적 위치를 기반으로 feature descriptor를 계속 업데이트한다.

마지막 cross-attention 레이어에서는 가장 많이 attention된 픽셀을 사용하여 raw disparity를 추정한다. Uniqueness 제약 조건을 준수하기 위한 Optimal Transport와 검색 공간 축소를 위한 attention mask를 이 레이어에만 추가한다.

Attention

Attention 모듈은 내적 유사도를 사용하여 일련의 query 벡터와 key 벡터 사이의 attention을 계산한 다음 value 벡터들에 가중치를 부여하는 데 사용된다.

저자들은 feature descriptor의 채널 차원 $C_e$를 $N_h$개의 그룹 $C_h = C_e / N_h$로 분할하여 feature descriptor의 표현성을 높이는 multi-head attention을 채택했다. 여기서 $C_h$는 각 head의 채널 차원이고 $N_h$는 head의 수이다. 따라서 각 head는 서로 다른 표현을 가질 수 있으며 head별로 유사도를 계산할 수 있다. 각 attention head $h$에 대힌 linear projection들은 feature descriptor $e_I$를 입력으로 사용하여 query 벡터 \(\mathcal{Q}_h\), key 벡터 \(\mathcal{K}_h\), value 벡터 \(\mathcal{V}_h\)를 계산하는 데 사용된다.

\[\begin{aligned} \mathcal{Q}_h &= W_{\mathcal{Q}_h} e_I + b_{\mathcal{Q}_h} \\ \mathcal{K}_h &= W_{\mathcal{K}_h} e_I + b_{\mathcal{K}_h} \\ \mathcal{V}_h &= W_{\mathcal{V}_h} e_I + b_{\mathcal{V}_h} \end{aligned}\]

여기서 \(W_{\mathcal{Q}_h}, W_{\mathcal{K}_h}, W_{\mathcal{V}_h} \in \mathbb{R}^{C_h \times C_h}\)이고 \(b_{\mathcal{Q}_h}, b_{\mathcal{K}_h}, b_{\mathcal{V}_h} \in \mathbb{R}^{C_h}\)이다. Softmax를 통해 유사도를 정규화하고 다음과 같이 $\alpha_h$를 얻는다.

\[\begin{equation} \alpha_h = \textrm{softmax} (\frac{\mathcal{Q}_h^\top \mathcal{K}_h}{\sqrt{C_h}}) \end{equation}\]

출력 값 벡터 \(\mathcal{V}_\mathcal{O}\)는 다음과 같이 계산할 수 있다.

\[\begin{equation} \mathcal{V}_\mathcal{O} = \mathcal{W}_\mathcal{O} \textrm{Concat} (\alpha_1 \mathcal{V}_1, \ldots, \alpha_{N_h} \mathcal{V}_{N_h}) + b_\mathcal{O} \end{equation}\]

여기서 \(\mathcal{W}_\mathcal{O} \in \mathbb{R}^{C_e \times C_e}\)이고 \(b_\mathcal{O} \in \mathbb{R}^{C_e}\)이다. 그런 다음 출력 값 벡터 \(\mathcal{V}_\mathcal{O}\)가 원래 feature descriptor에 추가되어 residual connection을 형성한다.

\[\begin{equation} e_I = e_I + \mathcal{V}_\mathcal{O} \end{equation}\]

Self-attention의 경우 \(\mathcal{Q}_h\), \(\mathcal{K}_h\), \(\mathcal{V}_h\)는 동일한 이미지에서 계산된다. Cross-attention의 경우 \(\mathcal{Q}_h\)는 소스 이미지에서 계산되고 \(\mathcal{K}_h\)와 \(\mathcal{V}_h\)는 타겟 이미지에서 계산된다. Cross-attention은 양방향으로 적용된다. (소스→타겟: 왼쪽→오른쪽 & 오른쪽→왼쪽)

Relative Positional Encoding

텍스처가 없는 넓은 영역에서는 픽셀 간의 유사성이 모호할 수 있다. 그러나 이러한 모호함은 가장자리와 같은 눈에 띄는 feature에 대한 상대적인 위치 정보를 고려함으로써 해결될 수 있다. 따라서 위치 인코딩 $e_p$를 통해 데이터에 대한 공간 정보를 제공한다. Shift-invariance로 인해 절대적인 픽셀 위치 대신 상대적인 픽셀 거리를 인코딩한다. 바닐라 Transformer에서는 절대적인 위치 인코딩 $e_p$가 feature descriptor에 직접 더해진다.

\[\begin{equation} e = e_I + e_p \end{equation}\]

이 경우, $i$번째 픽셀과 $j$번째 픽셀 사이의 attention은 다음과 같이 확장될 수 있다. (단순화를 위해 bias를 무시)

\[\begin{aligned} \alpha_{i,j} = &\; e_{I, i}^\top W_\mathcal{Q}^\top W_\mathcal{K} e_{I, j} + e_{I, i}^\top W_\mathcal{Q}^\top W_\mathcal{K} e_{p, j} \\ &+ e_{p, i}^\top W_\mathcal{Q}^\top W_\mathcal{K} e_{I, j} + e_{p, i}^\top W_\mathcal{Q}^\top W_\mathcal{K} e_{p, j} \end{aligned}\]

4번째 항은 전적으로 위치에 의존하므로 생략되어야 한다. 왜냐하면 disparity는 기본적으로 이미지 콘텐츠에 의존하기 때문이다. 대신 상대적 위치 인코딩을 사용하고 다음과 같이 4번째 항을 제거한다.

\[\begin{aligned} \alpha_{i,j} = &\; e_{I, i}^\top W_\mathcal{Q}^\top W_\mathcal{K} e_{I, j} \\ &+ e_{I, i}^\top W_\mathcal{Q}^\top W_\mathcal{K} e_{p, i-j} + e_{p, i-j}^\top W_\mathcal{Q}^\top W_\mathcal{K} e_{I, j} \end{aligned}\]

여기서 $e_{p, i−j}$는 $i$번째 픽셀과 $j$번째 픽셀 사이의 위치 인코딩이며, $e_{p, i−j} \ne e_{p, j−i}$이다. 직관적으로 attention은 콘텐츠 유사성과 상대적 거리에 따라 달라진다.

그러나 상대적 거리의 계산 비용은 이미지 너비 $I_w$의 제곱에 비례한다. 왜냐하면 각 픽셀에 대해 상대적 거리가 $I_w$개 있고 이 계산은 $I_w$번 수행되어야 하기 때문이다. 따라서 저자들은 비용을 선형으로 줄이는 효율적인 구현을 사용하였다.

Optimal Transport

오른쪽 이미지의 각 픽셀이 왼쪽 이미지의 최대 한 픽셀에 할당되는 stereo matching의 uniqueness 제약 조건을 적용하는 하드한 할당은 gradient flow를 막는다. 대조적으로, 엔트로피 정규화된 Optimal Transport는 소프트한 할당 및 미분 가능성으로 인해 이상적인 대안이며 sparse feature 및 semantic correspondence matching에 유용한 것으로 입증되었다. 길이 $I_w$의 두 주변 분포 $a$와 $b$의 cost matrix $M$이 주어지면 엔트로피 정규화된 Optimal Transport는 다음을 풀어 최적의 coupling matrix $\mathcal{T}$를 찾으려고 시도한다.

\[\begin{equation} \mathcal{T} = \underset{\mathcal{T} \in R_{+}^{I_w \times I_w}}{\arg \min} \sum_{i,j=1}^{I_w, I_w} \mathcal{T}_{i,j} M_{i,j} - \gamma E(\mathcal{T}) \\ \textrm{s.t.} \quad \mathcal{T} 1_{I_w} = a, \quad \mathcal{T}^\top 1_{I_w} = b \end{equation}\]

여기서 $E(\mathcal{T})$는 엔트로피 정규화이다. 두 개의 주변 분포 $a$, $b$가 균등 분포인 경우 $\mathcal{T}$는 소프트한 uniqueness 제약 조건을 부과하고 모호성을 완화하는 할당 문제에도 최적이다. 위 식의 해는 반복적인 Sinkhorn 알고리즘을 통해 찾을 수 있다. 직관적으로 $\mathcal{T}$의 값은 softmax attention과 유사한 쌍별 매칭 확률을 나타낸다. Occlusion(가려짐)으로 인해 일부 픽셀을 일치시킬 수 없다. SuperGlue를 따라 일치하지 않는 픽셀을 설정하는 비용을 직관적으로 나타내는 학습 가능한 파라미터 $\phi$를 사용하여 cost matrix를 augment한다.

STTR에서 cost matrix $M$은 cross-attention 모듈에 의해 계산된 attention의 음수로 설정되지만 softmax는 없다. 이는 Optimal Transport가 attention 값을 정규화하기 때문이다.

Attention Mask

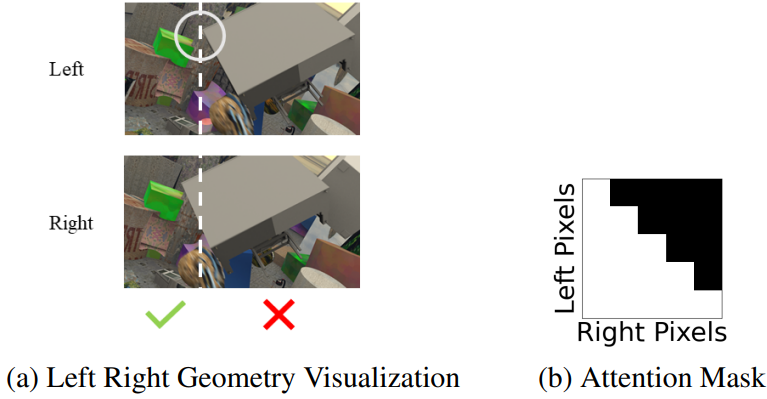
$x_L$, $x_R$을 각각 왼쪽 및 오른쪽 epipolar line에 대한 동일한 물리적 점의 투영된 위치라 하자 (왼쪽에서 오른쪽으로 $+x$). 스테레오 장비의 카메라 공간 배열은 rectification 후 모든 점에 대해 $x_R \le x_L$이 되도록 보장한다. 따라서 마지막 cross-attention 레이어에서는 왼쪽 이미지의 각 픽셀이 오른쪽 이미지의 동일한 좌표에서 더 왼쪽에 있는 픽셀에만 attention하는 것으로 충분하다. 이러한 제약을 적용하기 위해 attention에 lower-triangular binary mask를 도입한다.

Raw Disparity and Occlusion Regression

대부분의 이전 연구들에서는 모든 후보 disparity 값의 가중 합이 사용되었다. 대신 멀티모달 분포에 대해 강력한 수정된 승자 독식 접근 방식을 사용하여 disparity를 회귀한다.

Raw disparity는 Optimal Transport 할당 행렬 $\mathcal{T}$에서 가장 가능성 있는 매칭 위치 $k$를 찾고 그 주위에 3px window \(\mathcal{N}_3 (k)\)을 구축하여 계산된다. 합이 1이 되도록 3px window 내의 매칭 확률에 재정규화가 적용된다. 후보 disparity의 가중 합은 회귀된 raw disparity \(\tilde{d}_\textrm{raw} (k)\)이다. 할당 행렬 $\mathcal{T}$의 매칭 확률을 $t$로 표시하면 다음과 같다.

\[\begin{equation} \tilde{t}_l = \frac{t_l}{\sum_{l \in \mathcal{N}_3 (k)} t_l}, \quad \textrm{for} \; l \in \mathcal{N}_3 (k) \\ \tilde{d}_\textrm{raw} (k) = \sum_{l \in \mathcal{N}_3 (k)} d_l \tilde{t}_l \end{equation}\]

이 3px window 내의 확률 합계는 occlusion 확률의 역 형태로 현재 할당에 대한 네트워크의 신뢰도 추정치를 나타낸다. 그러므로 다음과 같은 정보를 사용하여 occlusion 확률 $p_\textrm{occ} (k)$를 회귀할 수 있다.

\[\begin{equation} p_\textrm{occ} (k) = 1 - \sum_{l \in \mathcal{N}_3 (k)} t_l \end{equation}\]

3. Context Adjustment Layer

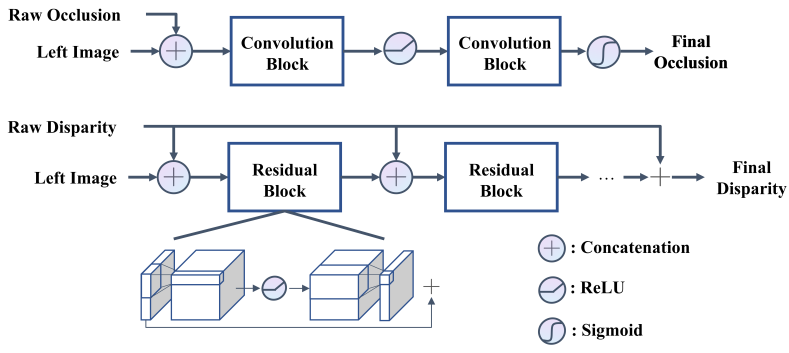
Raw disparity map과 raw occlusion map은 epipolar line에 대해 회귀되므로 여러 epipolar line에 대한 컨텍스트가 부족하다. 이를 완화하기 위해 convolution을 사용하여 epipolar line 사이의 정보를 사용하여 입력 이미지를 조건으로 추정 값을 조정한다. 컨텍스트 조정 레이어의 개요는 위 그림에 나와 있다.

Raw disparity map과 raw occlusion map은 먼저 채널 차원을 따라 왼쪽 이미지와 concatenate된다. 두 개의 convolution block이 occlusion 정보를 집계하는 데 사용되고 그 뒤에 ReLU가 사용된다. 최종 occlusion은 sigmoid에 의해 추정된다. ReLU 전에 채널 차원을 확장한 후 원래 채널 차원으로 복원하는 residual block을 통해 disparity가 개선된다. ReLU 이전의 확장은 더 나은 정보 흐름을 장려하는 것이다. 더 나은 컨디셔닝을 위해 raw disparity가 residual block과 반복적으로 concatenate된다. Residual block의 최종 출력은 긴 skip connection을 통해 raw disparity에 더해진다.

4. Loss

저자들은 occlusion으로 인해 일치하는 픽셀 집합 $\mathcal{M}$과 일치하지 않는 픽셀 집합 $\mathcal{U}$에 대해 할당 행렬 $\mathcal{T}$에서 제안된 Relative Response loss $L_{rr}$을 채택한다. 네트워크의 목표는 실제 대상 위치에 대한 attention을 극대화하는 것이다. Disparity는 가장 가까운 정수 픽셀 사이의 interpolation between을 사용하여 매칭 확률 $t^\ast$를 찾는다. 구체적으로, ground truth disparity $d_{gt,i}를 갖는 왼쪽 이미지의 $i$번째 픽셀에 대해 다음과 같다.

\[\begin{aligned} t_i^\ast &= \textrm{interp} (\mathcal{T}_i, p_i - d_{gt, i}) \\ L_rr &= \frac{1}{N_\mathcal{M}} \sum_{i \in \mathcal{M}} - \log (t_i^\ast) + \frac{1}{N_\mathcal{U}} \sum_{i \in \mathcal{U}} -\log (t_{i, \phi}) \end{aligned}\]

여기서 $\textrm{interp}$는 linear interpolation을 나타내고 $t_{i,\phi}$는 일치하지 않는 확률이다. 또한 Raw disparity와 최종 disparity 모두에 대해 smooth L1 loss $L_{d1,r}$과 $L_{d1,f}$를 사용한다. 최종 occlusion map은 binary-entropy loss $L_{be,f}를 통해 supervise된다. 총 loss는 다음과 같다.

\[\begin{equation} L = w_1 L_{rr} + w_2 L_{d1,r} + w_3 L_{d1,f} + w_4 L_{be,f} \end{equation}\]

여기서 $w$는 loss 가중치이다.

5. Memory-Feasible Implementation

Attention 메커니즘의 메모리 소비는 시퀀스 길이의 제곱에 비례한다. 특히 float32 정밀도 계산의 경우 총 $32 I_h I_w^2 N_h N$ bit의 메모리 소비가 발생한다. 예를 들어, $I_w = 960$, $I_h = 540$, $N_h = 8$인 경우 $N = 6$ layer Transformer를 학습시키면 약 216GB가 소비되며 이는 기존 하드웨어에서는 실용적이지 않다.

Sparse Transformer를 따라 각 self-attention과 cross-attention 레이어에 gradient checkpointing를 채택하여 forward pass 중에 중간 변수가 저장되지 않도록 한다. Backward pass 동안 checkpointed layer에 대해 forward pass를 다시 실행하여 gradient를 다시 계산한다. 따라서 메모리 소비는 attention 레이어 1개의 요구량에 의해 제한되며, 이는 이론적으로 네트워크가 attention 레이어 N의 수에 따라 무한하게 확장될 수 있도록 한다.

또한 학습 속도를 높이고 메모리 소비를 줄이기 위해 mixed-precision training을 사용한다. 마지막으로, attention stride $s > 1$를 사용하여 feature descriptor를 sparse하게 샘플링한다. 이는 feature map을 다운샘플링하는 것과 같다.

Complexity Analysis

기존 cost volume 패러다임에서 correlation 기반 네트워크는 $\mathcal{O} (I_h I_w D)$의 메모리 복잡도를 갖는 반면, 3D convolution 기반 네트워크는 $\mathcal{O} (I_h I_w D C)$의 메모리 복잡도를 갖는다. 여기서 $D$는 disparity의 최대값이고 $C$는 채널 크기이다. $D$는 일반적으로 $I_w$보다 작은 고정 값으로 설정되므로 범위 밖의 disparity 값을 예측하는 능력이 희생된다. STTR의 메모리 복잡도는 $\mathcal{O} (I_h I_w^2 / s^3)$이며, 이는 최대 disparity가 설정되지 않은 경우 trade-off를 제공한다. 주어진 $s$에서 STTR은 다양한 disparity 범위에서 일정한 메모리 소비로 실행된다. Inference 중에 $s$는 메모리 소비를 줄이고 작업 성능을 약간 희생하면서 최대 disparity 범위를 유지하는 더 큰 값으로 조정될 수 있다. 또한 저자들은 더 빠른 속도와 더 낮은 메모리 소비를 위해 $s$를 조정할 수 있는 유연성 없이 STTR의 경량화 구현을 도입하였다.

Experiments

• 데이터셋: Scene Flow, MPI Sintel, KITTI 2015, Middlebury 2014, SCARED
• 구현 디테일
  • self-attention layer와 cross-attention layer는 각각 6개, $C_e = 128$
  • Sinkhorn 알고리즘은 10번 실행됨
  • attention stride: $s = 3$
  • optimizer: Adam (weight decay = $10^{-4}$)
  • 가중치: $w_1 = w_2 = w_3 = w_4 = 1$
  • Scene Flow에서 15 epochs 사전 학습
  • learning rate: feature extractor와 Transformer는 $10^{-4}$, context adjustment layer는 $2 \times 10^{-4}$

1. Ablation Studies

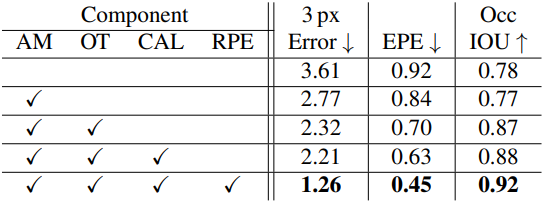
다음은 Scene Flow 데이터셋에서의 ablation study 결과이다.

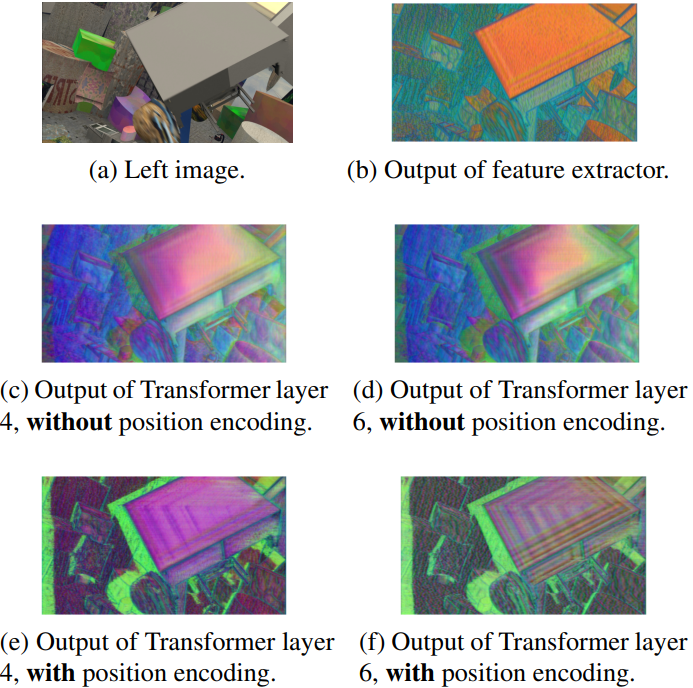
다음은 feature descriptor를 시각화한 것이다.

2. Comparison with Prior Work

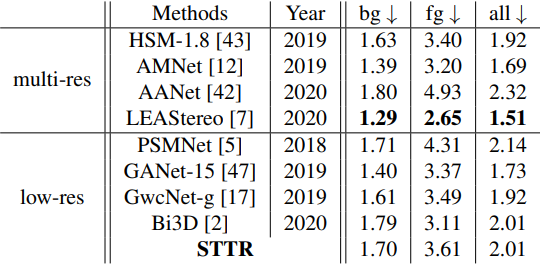
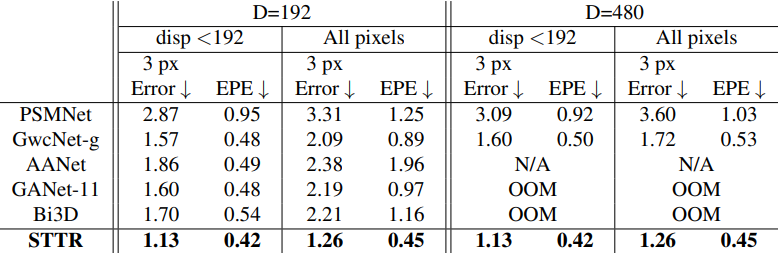
다음은 Scene Flow 데이터셋에서 다른 방법들과 비교한 표이다.

다음은 MPI Sintel, KITTI 2015, Middlebury 2014, SCARED 데이터셋에서 fine-tuning 없이 일반화 성능을 비교한 표이다.

다음은 KITTI 2015에서 3px / 5% Error를 비교한 표이다.