[논문리뷰] Street Gaussians for Modeling Dynamic Urban Scenes
ECCV 2024. [Paper] [Page]
Yunzhi Yan, Haotong Lin, Chenxu Zhou, Weijie Wang, Haiyang Sun, Kun Zhan, Xianpeng Lang, Xiaowei Zhou, Sida Peng
Zhejiang University | Li Auto
2 Jan 2024

Introduction
이미지에서 동적 3D 거리를 모델링하는 것은 도시 시뮬레이션, 자율 주행, 게임 등 중요한 응용 분야가 많다. 예를 들어, 도시 거리의 디지털 복사본을 자율주행 자동차의 시뮬레이션 환경으로 활용해 학습 및 테스트 비용을 절감할 수 있다. 이러한 애플리케이션을 사용하려면 캡처된 데이터에서 3D 거리 모델을 효율적으로 재구성하고 고품질의 새로운 뷰를 실시간으로 렌더링해야 한다.
NeRF를 사용하여 거리 장면을 재구성하려는 몇 가지 방법이 있었다. 모델링 능력을 향상시키기 위해 Block-NeRF는 거리를 여러 블록으로 나누고 각 블록을 NeRF 네트워크로 표현하였다. 이 전략을 사용하면 대규모 거리 장면을 사실적으로 렌더링할 수 있지만 Block-NeRF는 많은 양의 네트워크 파라미터로 인해 학습 시간이 길어진다. 게다가 자율주행 환경 시뮬레이션에서 중요한 측면인 거리의 역동적인 차량을 처리할 수 없다.
최근 일부 방법에서는 동적 거리 장면을 움직이는 자동차와 정적 배경으로 표현하는 것을 제안하였다. 동적인 자동차를 다루기 위해 이 방법들은 추적된 차량 포즈를 활용하여 관찰 공간과 표준 공간 사이의 매핑을 설정하고 NeRF 네트워크를 사용하여 자동차의 기하학적 구조와 외관을 모델링하였다. 결과적으로 이러한 방법은 추적된 bounding box의 정확성에 민감하며, 여전히 높은 학습 비용과 낮은 렌더링 속도로 인해 제한된다.
본 논문에서는 이미지로부터 동적 3D 거리 장면을 재구성하기 위한 새롭고 명시적인 장면 표현을 제안하였다. 기본 아이디어는 포인트 클라우드를 활용하여 동적 장면을 구축하는 것이다. 이를 통해 추적된 차량 포즈의 정확도에 대한 의존도를 줄이면서 학습 및 렌더링 효율성을 크게 높일 수 있다. 구체적으로 도시의 거리 장면을 정지된 배경과 움직이는 차량으로 분해하여 3D Gaussian을 기반으로 별도로 제작한다. 차량의 역학을 처리하기 위해 각 포인트가 학습 가능한 3D Gaussian 파라미터를 저장하는 포인트의 집합으로 형상을 모델링하며, 이 포인트들은 최적화 가능한 차량 포즈를 가지고 있다. 또한, 시간에 따라 변하는 외관은 시계열 함수를 사용하여 모든 timestep에서 spherical harmonics(SH)를 예측하는 4D SH 모델로 표현된다. 동적인 Gaussian 표현 덕분에 30분 안에 도시의 거리를 충실하게 재구성하고 실시간 렌더링(133FPS @ 1066$\times$1600)을 달성할 수 있다.
저자들은 제안된 장면 표현을 기반으로 추적된 포즈 최적화 전략을 추가로 개발하였다. 최적화 가능한 포즈 입력은 렌더링된 동영상과 입력 동영상 간의 더 나은 정렬을 보장한다. 본 논문의 방법은 명시적 표현에 의한 더 나은 기울기 전파 덕분에 기존 추적기의 포즈만 활용하면서 실제 포즈로 달성한 결과와 비슷한 결과를 얻을 수 있다.
Method
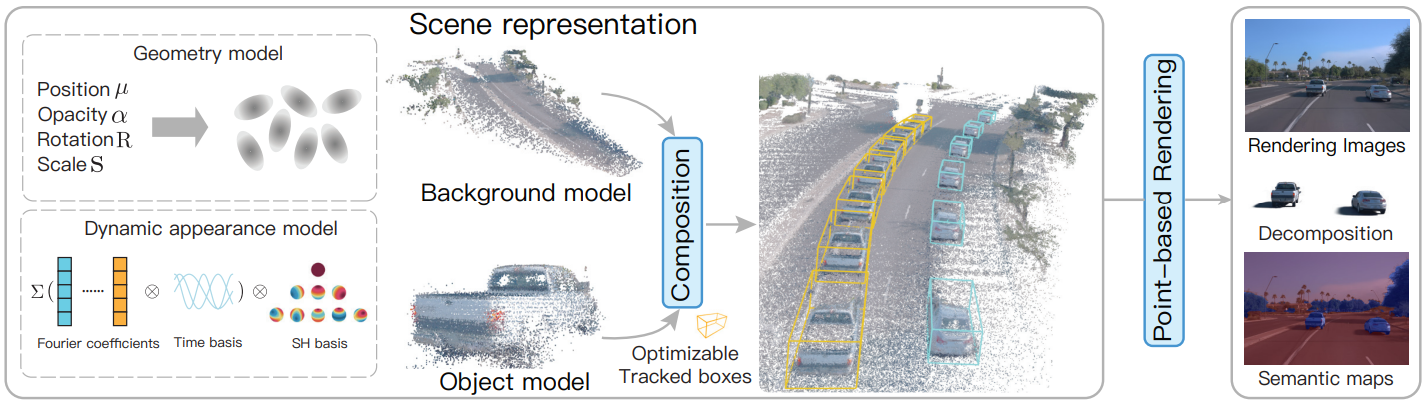
본 논문의 목표는 도시의 거리 장면에서 움직이는 차량에서 캡처한 일련의 이미지를 바탕으로 입력 timestep과 시점에 대해 사실적인 이미지를 생성할 수 있는 모델을 개발하는 것이다. 저자들은 동적인 거리 장면을 표현하기 위해 특별히 설계된 Street Gaussian이라는 새로운 장면 표현을 제안하였다. 위 그림에서 볼 수 있듯이 동적 도시 거리 장면을 포인트 클라우드의 집합으로 표현하며, 각각은 정적 배경 또는 움직이는 차량에 해당한다. 명시적인 포인트 기반 표현을 통해 별도의 모델을 쉽게 구성할 수 있어 실시간 렌더링은 물론 편집 애플리케이션을 위한 전경 객체를 분리하는 것도 가능하다. 제안된 장면 표현은 추적된 차량 포즈 최적화 전략으로 기존 추적기로 추적된 차량 포즈와 함께 RGB 이미지만을 사용하여 효과적으로 학습될 수 있다.
1. Street Gaussians
실시간으로 빠르게 구성하고 렌더링할 수 있는 동적 장면 표현을 찾는 것이 목표이다. 이전 방법들은 일반적으로 낮은 학습 및 렌더링 속도와 정확한 차량 포즈 문제에 직면했다. 이 문제를 해결하기 위해 저자들은 3D Gaussian을 기반으로 구축된 Street Gaussian이라는 새로운 명시적 장면 표현을 제안하였다. Street Gaussians에서는 정적 배경과 움직이는 차량 객체를 별도의 뉴럴 포인트 클라우드로 표현한다.
Background model
Background model은 월드 좌표계에서의 포인트의 집합으로 표시된다. 각 포인트에는 3D Gaussian이 할당되어 연속적인 장면 형상과 색상을 부드럽게 표현한다. Gaussian 파라미터는 공분산 행렬 \(\boldsymbol{\Sigma}_b\)와 평균값을 나타내는 위치 벡터 \(\boldsymbol{\mu}_b \in \mathbb{R}^3\)으로 구성된다. 최적화 중에 유효하지 않은 공분산 행렬을 피하기 위해 각 공분산 행렬은 스케일링 행렬 \(\mathbf{S}_b\)와 회전 행렬 \(\mathbf{R}_b\)로 분리된다. 여기서 \(\mathbf{S}_b\)는 대각 성분으로 특징지어진다. \(\mathbf{R}_b\)는 단위 quaternion으로 변환된다. 공분산 행렬 \(\boldsymbol{\Sigma}_b\)는 \(\mathbf{S}_b\)와 \(\mathbf{R}_b\)에서 다음과 같이 복구할 수 있다.
\[\begin{equation} \boldsymbol{\Sigma}_b = \mathbf{R}_b \mathbf{S}_b \mathbf{S}_b^\top \mathbf{R}_b^\top \end{equation}\]위치 및 공분산 행렬 외에도 각 Gaussian에는 불투명도 값 $\alpha_b \in \mathbb{R}$과 spherical harmonics(SH) 계수 집합 \(\mathbf{z}_b = (z_{m,l})_{l: 0 \le \ell \le \ell_\textrm{max}}^{m:−\ell \le m \le \ell}\)가 할당되며, 장면 형상과 모양을 나타낸다. 뷰에 따른 색상을 얻으려면 SH 계수에 뷰 방향에서 투영된 SH basis function을 더 곱해야 한다. 3D semantic 정보를 표현하기 위해 각 포인트에는 semantic logit \(\boldsymbol{\beta}_b \in \mathbb{R}^M\)이 추가된다. 여기서 $M$은 semantic 클래스의 수이다.
Object model
$N$개의 움직이는 차량이 포함된 장면을 생각해 보자. 각 객체는 최적화 가능한 차량 포즈 세트와 포인트 클라우드로 표현되며, 각 포인트에는 3D Gaussian, semantic logit, 동적 외관 모델이 할당된다.
객체와 배경 모두의 Gaussian 속성은 유사하며 불투명도 $\alpha_o$와 스케일링 행렬 \(\mathbf{S}_o\)는 의미가 동일하다. 그러나 위치, 회전, 외관은 background model과 다르게 모델링된다. 위치 \(\boldsymbol{\mu}_o\)와 회전 \(\mathbf{R}_o\)는 객체 로컬 좌표계에서 정의된다. 이를 월드 좌표계(배경 좌표계)로 변환하기 위해 객체에 대한 추적된 포즈의 정의를 도입한다. 구체적으로, 차량의 추적된 포즈는 rotation matrix \(\{\mathbf{R}_t\}_{t=1}^{N_t}\)와 translation vector \(\{\mathbf{T}_t\}_{t=1}^{N_t}\)의 집합으로 정의된다. 여기서 $N_t$는 프레임 수이다. Transformation은 다음과 같이 정의할 수 있다.
\[\begin{aligned} \boldsymbol{\mu}_w &= \mathbf{R}_t \boldsymbol{\mu}_o + \mathbf{T}_t \\ \mathbf{R}_w &= \mathbf{R}_o \mathbf{R}_t^\top \end{aligned}\]여기서 \(\boldsymbol{\mu}_w\)와 \(\mathbf{R}_w\)는 각각 세계 좌표계에서 해당 객체 Gaussian의 위치와 회전이다. Transformation 후 객체의 공분산 행렬 $\boldsymbol{\Sigma}_w$는
\[\begin{equation} \boldsymbol{\Sigma}_w = \mathbf{R}_w \mathbf{S}_o \mathbf{S}_o^\top \mathbf{R}_w^\top \end{equation}\]로 얻을 수 있다. 또한 저자들은 기성 추적기에서 추적된 차량 포즈에 잡음이 많다는 것을 발견했다. 이 문제를 해결하기 위해 추적된 차량 포즈를 학습 가능한 파라미터로 처리한다.
SH 계수를 사용하여 물체의 외관을 단순히 표현하는 것만으로는 움직이는 차량의 모양을 모델링하는 데 충분하지 않다. 왜냐하면 움직이는 차량의 모양은 글로벌 장면에서의 위치에 영향을 받기 때문이다. 한 가지 간단한 해결책은 별도의 SH를 사용하여 각 timestep에 대한 객체를 표현하는 것이다. 그러나 이렇게 표현하면 저장 비용이 크게 증가한다. 대신, 각 SH 계수 $z_{m,l}$을 푸리에 변환 계수의 집합 $\mathbf{f} \in \mathbb{R}^k$로 대체하여 4D SH 모델을 도입한다. 여기서 $k$는 푸리에 계수의 수이다. Timestep $t$가 주어지면 $z_{m,l}$은 Inverse Discrete Fourier Transform을 수행하여 복구된다.
\[\begin{equation} z_{m,l} = \sum_{i=0}^{k-1} \mathbf{f}_i \cos \bigg( \frac{i \pi}{N_t} t \bigg) \end{equation}\]제안된 모델을 사용하여 높은 저장 비용 없이 시간 정보를 외관으로 인코딩한다.
Object model의 semantic 표현은 background model의 semantic 표현과 다르다. 가장 큰 차이점은 object model의 semantic이 background model과 같은 $M$차원 벡터 \(\boldsymbol{\beta}_b\)가 아닌 1차원 스칼라 $\beta_o$라는 점이다. 전경 객체 차량 모델에 대한 이 semantic 모델은 객체에 대한 semantic 카테고리가 두 개, 즉 차량과 비차량만 있기 때문에 이진 분류 또는 신뢰도 예측 문제로 간주될 수 있다.
2. Rendering of Street Gaussians
Street Gaussian을 렌더링하려면 각 모델의 기여도를 집계하여 최종 이미지를 렌더링해야 한다. 모든 포인트 클라우드를 2D 이미지 공간에 투영하여 Street Gaussian을 렌더링할 수 있다. 구체적으로, 렌더링된 timestep $t$가 주어지면 먼저 SH를 계산하고 추적된 차량 포즈 $(\mathbf{R}_t, \mathbf{T}_t)$에 따라 객체 포인트 클라우드를 월드 좌표계로 변환한다. 그런 다음 배경 포인트 클라우드와 변환된 객체 포인트 클라우드를 연결하여 새로운 포인트 클라우드를 형성한다. 이 포인트 클라우드를 camera extrinsic $\mathbf{W}$와 camera intrinsic $\mathbf{K}$를 사용하여 2D 이미지 공간에 투영하기 위해 포인트 클라우드의 각 포인트에 대해 2D Gaussian을 계산한다.
\[\begin{aligned} \boldsymbol{\mu}^\prime &= \mathbf{K} \mathbf{W} \boldsymbol{\mu} \\ \boldsymbol{\Sigma}^\prime &= \mathbf{J} \mathbf{W} \boldsymbol{\Sigma} \mathbf{W}^\top \mathbf{J}^\top \end{aligned}\]여기서 $\mathbf{J}$는 $\mathbf{K}$의 Jacobian 행렬이다. \(\boldsymbol{\mu}^\prime\)와 \(\boldsymbol{\Sigma}^\prime\)는 각각 2D 이미지 공간의 위치 행렬과 공분산 행렬이다. 각 픽셀에 대한 포인트 기반 $\alpha$-blending은 색상 $\mathbf{c}$를 계산하는 데 사용된다.
\[\begin{equation} \mathbf{c} = \sum_{i \in N} \mathbf{c}_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]여기서 $\alpha_i$는 불투명도 $\alpha$에 2D Gaussian의 확률을 곱한 값이고 \(\mathbf{c}_i\)는 뷰 방향에 따른 SH $\mathbf{z}$에서 계산된 색상이다.
Semantic map은 위 식의 색상 $c$를 semantic logit $\boldsymbol{\beta}$로 변경하여 간단하게 렌더링할 수 있다.
3. Training
Tracking pose optimization
렌더링하는 동안 객체 Gaussian의 위치 및 공분산 행렬은 추적된 포즈 파라미터와 밀접한 상관 관계가 있다. 그러나 추적기 모델에 의해 생성된 bounding box에는 일반적으로 잡음이 있다. 장면 표현을 최적화하기 위해 이를 직접 사용하면 렌더링 품질이 저하된다. 따라서 각 transformation 행렬에 학습 가능한 transformation을 추가하여 추적된 포즈를 학습 가능한 파라미터로 처리한다. 구체적으로, \(\mathbf{R}_t\)와 \(\mathbf{T}_t\)는 다음과 같이 정의되는 \(\mathbf{R}_t^\prime\)와 \(\mathbf{T}_t^\prime\)로 대체된다.
\[\begin{aligned} \mathbf{R}_t^\prime &= \mathbf{R}_t \Delta \mathbf{R}_t \\ \mathbf{T}_t^\prime &= \mathbf{T}_t + \Delta \mathbf{T}_t \end{aligned}\]여기서 \(\Delta \mathbf{R}_t\)와 \(\Delta \mathbf{T}_t\)는 학습 가능한 transformation이다. \(\Delta \mathbf{T}_t\)는 3D 벡터로, \(\Delta \mathbf{R}_t\)는 yaw 오프셋 각도 \(\Delta \theta_t\)에서 변환된 회전 행렬로 나타낸다. 이러한 transformation의 기울기는 역전파 중에 추가 계산이 필요하지 않은 암시적 함수나 중간 프로세스 없이 직접 얻을 수 있다.
Loss function
다음 손실 함수를 사용하여 장면 표현과 추적된 포즈를 공동으로 최적화한다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{color} + \lambda_1 \mathcal{L}_\textrm{sem} + \lambda_2 \mathcal{L}_\textrm{reg} \end{equation}\]위 식에서 \(\mathcal{L}_\textrm{color}\)는 렌더링된 이미지와 관찰된 이미지 간의 재구성 loss이다. \(\mathcal{L}_\textrm{sem}\)은 렌더링된 semantic logit과 입력 2D 의미론적 분할 예측 사이의 per-pixel softmaxcross-entropy loss이다. 잡음이 있는 semantic label 입력이 형상에 영향을 미치는 것을 방지하기 위해 $\mathcal{L}_\textrm{sem}$의 $\alpha$로의 기울기를 중지한다. \(\mathcal{L}_\textrm{reg}\)는 floater를 제거하고 분해 효과를 향상시키는 데 사용되는 엔트로피 정규화 항이다. 실제로 \(\lambda_1 = 0.1\), \(\lambda_2 = 0.1\)로 설정했다.
Experiments
- 데이터셋: Waymo Open Dataset, KITTI
- 구현 디테일
- 초기화: LiDAR 포인트 클라우드
- object model: bounding box 내의 포인트로 초기화
- background model: 나머지 포인트 중 보이는 포인트만 사용
- 색상은 이미지 평면의 픽셀 값을 쿼리하여 사용
- 먼 영역은 SfM 포인트 클라우드를 통합
- Densification and pruning
- 장면의 반경: background model은 LiDAR 포인트 클라우드로, object model은 bounding box 스케일로 결정
- 최적화 중에 bounding box 밖의 포인트들은 pruning
- iteration: 30,000
- optimizer: Adam
- learning rate: \(\Delta \mathbf{T}_t\)는 0.005, \(\Delta \mathbf{R}_t\)는 0.001
- GPU: RTX 4090 GPU 1개
- 초기화: LiDAR 포인트 클라우드
1. Comparisons with the State-of-the-art
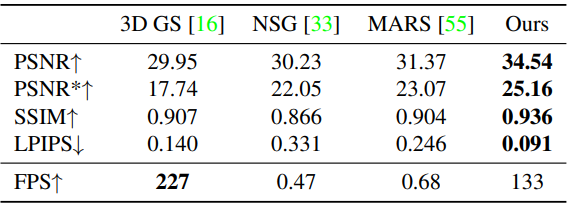
다음은 Waymo에서의 결과를 정량적으로 비교한 표이다.
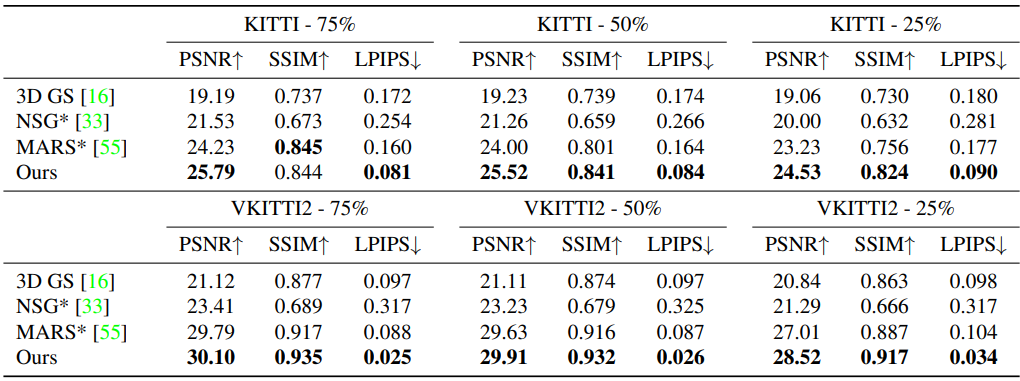
다음은 KITTI와 VKITTI2에서의 결과를 정량적으로 비교한 표이다.
다음은 Waymo에서의 결과를 비교한 것이다.

다음은 KITTI에서의 결과를 비교한 것이다.

2. Ablations and Analysis
다음은 Waymo에서의 ablation study 결과이다.
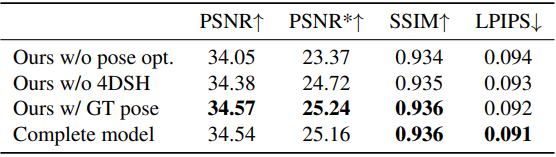

다음은 4D SH 모델에 대한 ablation study 결과이다. (Waymo)

3. Applications
다음은 KITTI에서의 객체 분리 결과를 비교한 것이다.

다음은 Waymo에서의 장면 편집 결과이다.

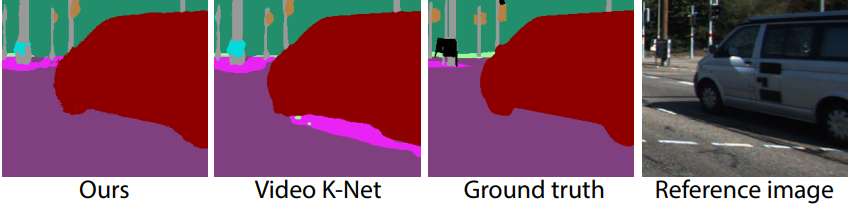
다음은 KITTI에서의 semantic segmentation 결과를 비교한 것이다.