[논문리뷰] STaR: Bootstrapping Reasoning With Reasoning

NeurIPS 2022. [Paper]
Eric Zelikman, Yuhuai Wu, Jesse Mu, Noah D. Goodman
Stanford University | Google Research
28 Mar 2022

Introduction

인간의 의사결정은 종종 길고 복잡한 사고 과정을 거쳐 이루어진다. 최근 연구에 따르면, 명시적인 중간 추론 단계(rationale)를 포함시키는 것이 LLM의 성능을 향상시킬 수 있다는 것이 밝혀졌다. 수학적 추론, 상식 추론, 코드 평가, 사회적 편향 추론, 자연어 추론 등 다양한 task에서 LLM이 최종 답변을 제시하기 전에 명시적인 이유를 생성하는 이유 생성(rationale generation)은 유용하다.

그러나 현재 이유 생성을 유도하는 주요 방법 두 가지에는 각각 심각한 단점이 존재한다. 첫 번째 접근법은 인간 주석자들이 수작업으로 또는 수작업 템플릿을 통해 fine-tuning 데이터셋을 구성하는 것이다. 그러나 수작업 방식은 비용이 많이 들고, 템플릿 기반 방식은 이미 일반적인 해결책이 알려져 있거나 합리적인 하드코딩된 휴리스틱을 만들 수 있을 때만 작동한다. 이에 대한 대안으로는, in-context learning을 활용하는 방법이 있으며, 이유 없이 직접 정답을 요구하는 프롬프트보다 정확도를 향상시키는 것으로 나타났다. 그러나 in-context learning 기법들은 일반적으로 더 큰 데이터셋을 활용하여 정답을 직접 예측하도록 fine-tuning된 모델보다는 성능이 떨어지는 경향이 있다.

본 논문에서는 기존 접근 방식과는 다른 방법을 채택하였다. LLM이 이미 갖고 있는 추론 능력을 활용하여, 고품질의 이유(rationale)를 생성하는 능력을 점진적으로 부트스트랩하는 방식을 사용한다. 구체적으로, 먼저 few-shot 프롬프트를 사용하여 LLM이 스스로 이유를 생성하게 하고, 그 이유가 정답에 도달한 경우에만 해당 이유를 사용하여 모델을 추가로 fine-tuning한다. 이 과정을 반복하면서, 매번 향상된 모델을 이용해 다음 학습 데이터를 생성한다. 이유 생성 능력이 향상되면 학습 데이터의 질도 향상되고, 학습 데이터의 질이 향상되면 다시 이유 생성 능력이 좋아진다.

그러나 모델이 정답을 맞히지 못한 문제들에 대해서는 직접적인 학습 신호를 받지 못하기 때문에, 이 루프는 결국 학습 데이터셋 내의 새로운 문제들을 해결하는 데 실패하게 된다. 이 문제를 해결하기 위해, 본 논문은 합리화(rationalization)라는 방법을 제안하였다. 이는 모델이 정답을 맞히지 못한 문제들에 대해 정답을 제공한 상태에서 새로운 이유를 생성하도록 하는 것이다. 즉, 정답을 알고 있는 상태에서 역추론을 수행하게 하여, 모델이 보다 유용한 이유를 생성할 수 있게 한다. 이렇게 생성된 이유들은 새로운 학습 데이터로 수집되며, 이는 전체 정확도를 종종 향상시킨다.

본 논문은 이러한 방식을 통해 Self-Taught Reasoner (STaR)라는 방법을 개발하였다. STaR는 모델이 스스로 이유를 생성하는 방법을 학습할 수 있게 해 주는 확장 가능한 부트스트랩 방법이며, 동시에 점점 더 어려운 문제들을 해결하는 능력도 키울 수 있다.

구체적으로, 다음의 과정을 반복한다.

1. 현재 모델의 이유 생성 능력을 사용해 데이터셋 문제들을 해결하고, 그 결과로 fine-tuning용 데이터셋을 구성한다.
2. 모델이 해결하지 못한 문제들에 대해서는 정답을 제공하여 새로운 이유를 생성하고 (합리화), 이를 데이터셋에 추가한다.
3. 이 결합된 데이터셋을 기반으로 모델을 다시 fine-tuning한다.

STaR는 산술 문제, 수학 서술형 문제, 상식 추론에서 소수의 few-shot 프롬프트만을 가지고도 대규모 이유 데이터셋으로 확장 가능하며, 성능이 눈에 띄게 향상된다. 예를 들어, CommonsenseQA 벤치마크에서는 STaR가 few-shot baseline보다 35.9%, 정답만을 직접 예측하도록 fine-tuning된 baseline보다 12.5% 더 나은 성능을 보였으며, 30배 더 큰 모델과 거의 동등한 성능을 달성했다.

Method

1. Rationale Generation Bootstrapping (STaR Without Rationalization)

사전 학습된 LLM $M$과 문제 $x$와 답 $y$의 쌍으로 구성된 초기 데이터 집합 \(\mathcal{D} = \{(x_i, y_i)\}_{i=1}^D\)가 주어진다. 먼저, 중간 이유 $r$을 갖는 예제들로 구성된 작은 프롬프트 세트 $\mathcal{P}$로 시작한다.

\[\begin{equation} \mathcal{P} = \{(x_i^p, r_i^p, y_i^p)\}_{i=1}^P, \quad \textrm{where} \; P \ll D \end{equation}\]

표준적인 few-shot prompting과 같이 $\mathcal{P}$를 $\mathcal{D}$의 각 예제에 concat한다.

\[\begin{equation} x_i = (x_1^p, r_1^p, y_1^p, \ldots, x_P^p, r_P^p, y_P^p, x_i) \end{equation}\]

이를 통해 모델은 $x_i$에 대한 이유 \(\hat{r}_i\)와 답 \(\hat{y}_i\)를 생성한다. 정답으로 이어지는 이유는 오답으로 이어지는 이유보다 품질이 더 좋다고 가정한다. 따라서 생성된 이유를 필터링하여 정답으로 이어지는 이유만 포함한다 (\(\hat{y}_i = y_i\)).

필터링된 데이터셋을 기반으로 기본 모델 $M$을 fine-tuning한 후, 새롭게 fine-tuning된 모델을 사용하여 새로운 이유를 생성하여 이 과정을 다시 시작한다. 성능이 안정화될 때까지 이 과정을 반복한다. 이 과정에서 새로운 데이터셋을 수집하면 하나의 모델을 계속 학습하는 대신, overfitting을 방지하기 위해 원래 사전 학습된 모델 $M$을 사용하여 학습한다.

STaR는 RL 스타일의 policy gradient의 근사치로 볼 수 있다. $M$은 discrete latent variable model

\[\begin{equation} p_M (y \, \vert \, x) = \sum_r p(r \, \vert \, x) p(y \, \vert \, x, r) \end{equation}\]

로 볼 수 있다. 즉, $M$은 $y$를 예측하기 전에 $r$을 먼저 샘플링한다. 이제 reward function $\unicode{x1D7D9}(\hat{y} = y)$가 주어지면 데이터셋 전체의 총 reward 기대값은 다음과 같다.

\[\begin{aligned} J (M, X, Y) &= \sum_i \mathbb{E}_{\hat{r}_i, \hat{y}_i \sim p_M (\cdot \vert x_i)} \unicode{x1D7D9} (\hat{y}_i = y_i) \\ \nabla J (M, X, Y) &= \sum_i \mathbb{E}_{\hat{r}_i, \hat{y}_i \sim p_M (\cdot \vert x_i)} [\unicode{x1D7D9} (\hat{y}_i = y_i) \cdot \nabla \log p_M (\hat{y}_i, \hat{r}_i \, \vert \, x_i)] \end{aligned}\]

Indicator function는 정답 $y_i$로 이어지지 않는 모든 샘플링된 이유에 대한 gradient를 버린다. 이것이 STaR의 필터링 프로세스이다. 따라서 STaR는 \((\hat{r}_i, \hat{y}_i)\)의 샘플을 greedy decoding하여 이 추정치의 분산을 줄이고, 동일한 데이터 batch에서 여러 gradient step을 수행하여 $J$를 근사한다. 이러한 근사화로 인해 STaR는 표준 LLM 학습 장비로 구현할 수 있는 간단하고 광범위하게 적용 가능한 방법이 된다.

2. Rationalization

이유 생성 부트스트래핑 알고리즘에는 한계가 있다. 모델은 정답으로 답한 예제에 대해서만 학습되기 때문에, 모델이 학습 세트에서 새로운 문제를 해결하지 못하면 더 이상 개선이 되지 못한다. 이는 알고리즘이 실패한 예제에서 학습 신호를 얻을 수 없기 때문이다.

Q: Where do you put your grapes just before checking out?
Answer Choices:
(a) mouth
(b) grocery cart (CORRECT)
(c) super market
(d) fruit basket
(e) fruit market
A: The answer should be the place where grocery items are placed before checking out. Of the above choices, grocery cart makes the most sense for holding grocery items. Therefore, the answer is grocery cart (b).

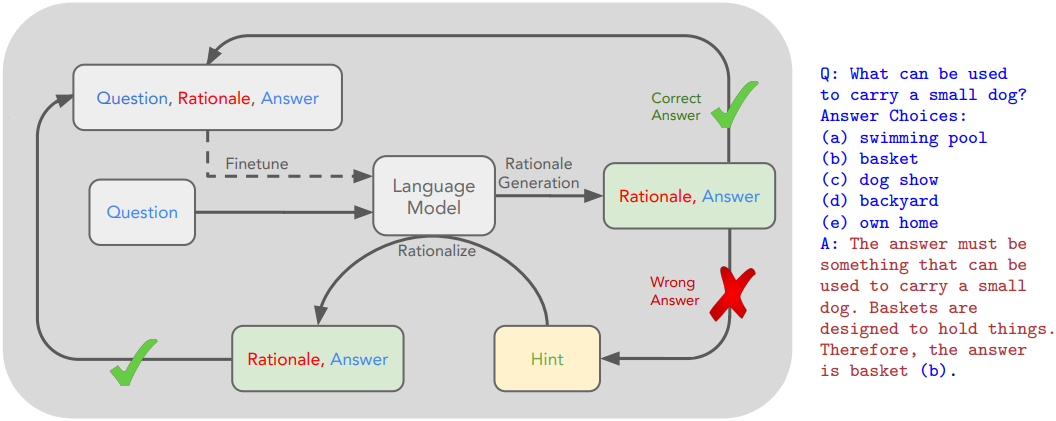
본 논문은 합리화(rationalization)라고 부르는 기법을 제안하였다. 구체적으로, 모델에 정답을 힌트로 제공하고 이전 이유 생성 단계와 동일한 방식으로 이유를 생성하도록 한다. 답이 주어지면 모델은 역추론을 통해 정답으로 이어지는 이유를 더 쉽게 생성할 수 있다. 예를 들어, 위 예시에서 “(b) grocery cart”가 정답이라는 힌트를 프롬프트에 제공하여 이유를 생성한다. 모델이 이유 생성을 통해 해결하지 못한 문제에는 합리화를 적용한다. 합리화로 생성된 이유를 데이터셋에 추가할 때는, 마치 모델이 힌트 없이 이유를 도출한 것처럼 해당 프롬프트에 힌트를 포함하지 않는다. 필터링 후, 이전에 생성된 데이터셋과 합리화를 통해 생성된 데이터셋을 결합하여 fine-tuning한다.

Algorithm 1은 전체 알고리즘이며, 파란색 부분은 합리화에 해당한다. 합리화로 생성된 데이터셋에 대한 fine-tuning은 모델을 fine-tuning 데이터셋에서는 나타나지 않았을 어려운 문제에 노출시키는 중요한 이점을 제공한다. 이는 모델이 실패했던 문제에 대해 “틀에서 벗어난 사고”를 하도록 유도하는 것으로 이해할 수 있다. 합리화의 두 번째 이점은 데이터셋 크기가 증가한다는 것이다.

Experiments

1. Symbolic Reasoning: Results on Arithmetic

실험에 사용된 산술 문제는 두 개의 n자리 정수의 합을 계산하는 것이다. 아래는 3자리 정수의 합을 구하는 예시이다.

Input:
6 2 4 + 2 5 9
Target:
<scratch>
6 2 4 + 2 5 9 , C: 0
2 + 5 , 3 C: 1
6 + 2 , 8 3 C: 0
, 8 8 3 C: 0
0 8 8 3
</scratch>
8 8 3

다음은 합리화 유무에 따른 STaR의 정확도를 자릿수에 따라 비교한 그래프이다.

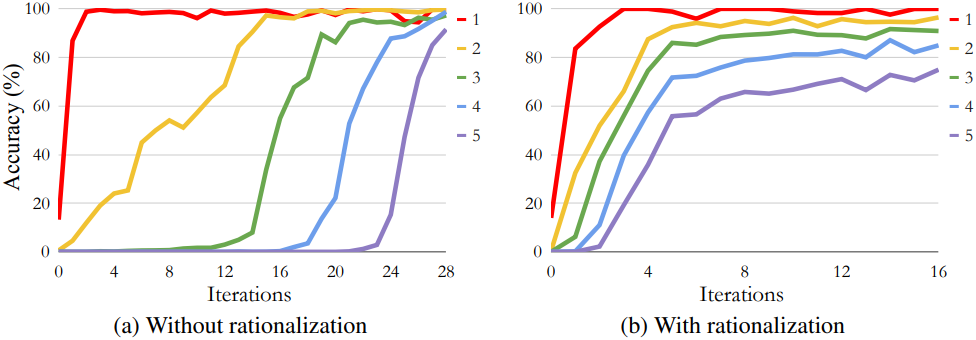
다음은 20번째 iteration에 추가 자릿수를 도입하였을 때, 합리화를 사용한 STaR의 정확도를 나타낸 그래프이다.

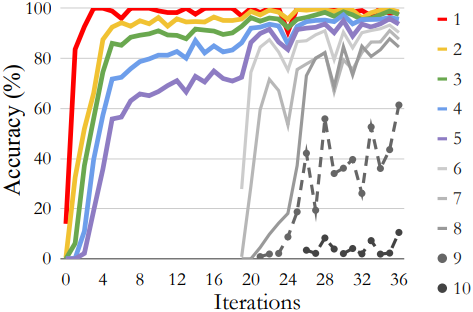
2. Natural Language Reasoning: Commonsense Question Answering

다음은 CommonsesenseQA (CQA)에서의 자연어 추론 성능을 비교한 결과이다.

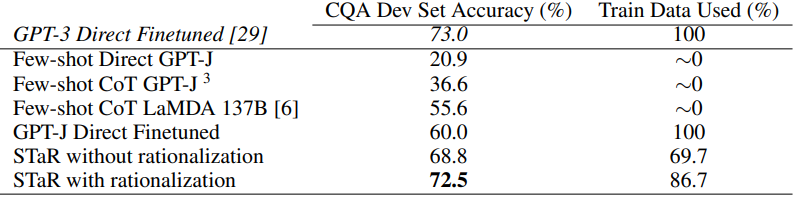
3. Mathematical Reasoning in Language: Grade School Math

다음은 GSM8K에서의 수학적 추론 성능을 비교한 결과이다.

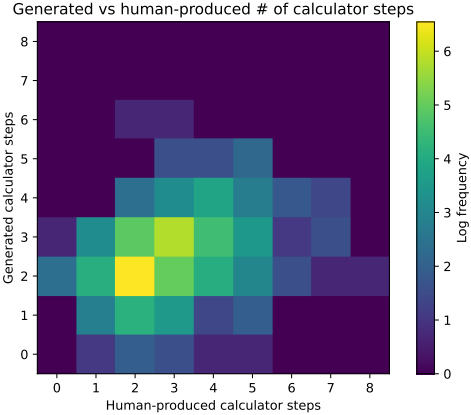
다음은 학습 세트의 예제를 풀기 위해 모델이 생성한 계산 단계 수를 GT에서 사용된 단계 수와 비교한 것이다.