[논문리뷰] StableNormal: Reducing Diffusion Variance for Stable and Sharp Normal
SIGGRAPH Asia 2024. [Paper] [Page] [Github]
Chongjie Ye, Lingteng Qiu, Xiaodong Gu, Qi Zuo, Yushuang Wu, Zilong Dong, Liefeng Bo, Yuliang Xiu, Xiaoguang Han
The Chinese University of Hongkong | Alibaba Group | Max Planck Institute for Intelligent Systems
24 Jun 2024
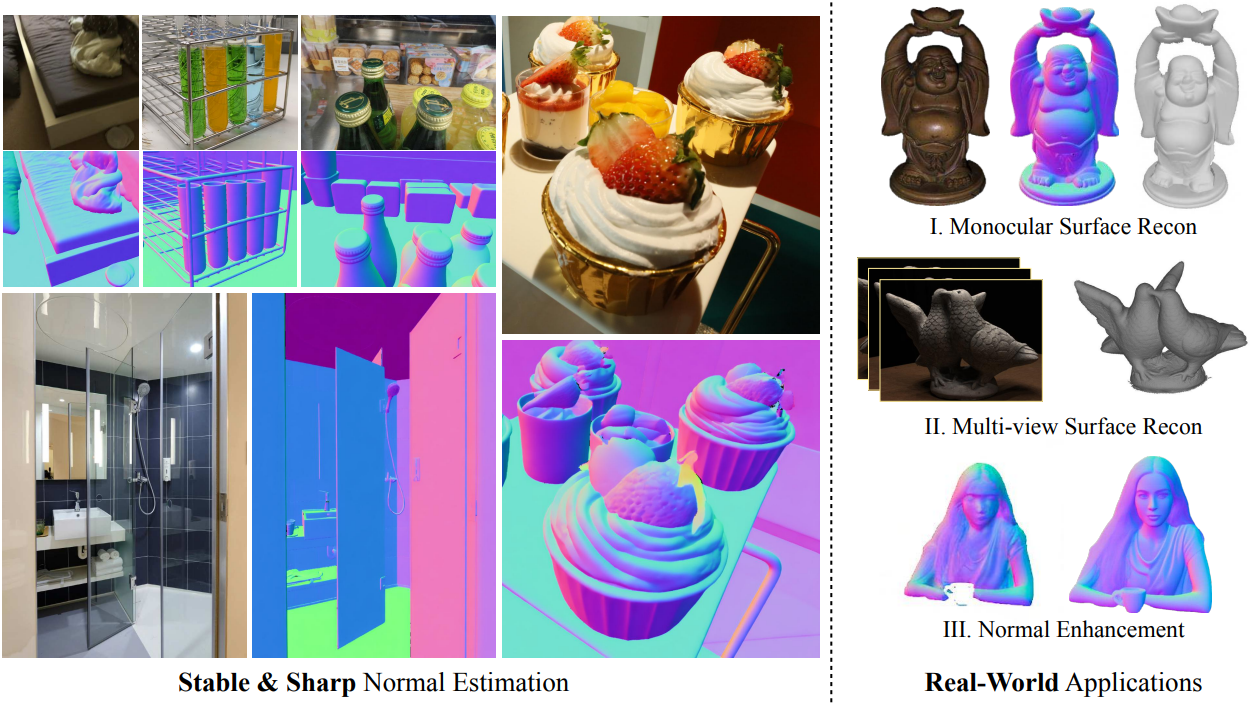
Introduction
Image-to-normal task는 여러 연구에서 활발히 연구되어 왔다. 최근, 대규모 데이터셋을 학습하는 diffusion 기반 이미지 생성 모델의 발전으로 인해 비전 분야의 관심은 diffusion prior를 활용하여 normal을 추정하는 방향으로 옮겨갔다. 이러한 노력의 결과로 선명한 normal 결과가 도출되었지만, 시간적 불일치가 존재하며, 앙상블을 거친 후에도 결과가 실제 normal 데이터와 크게 차이가 난다. 즉, 결과가 선명하지만 정확하거나 안정적이지는 않다.
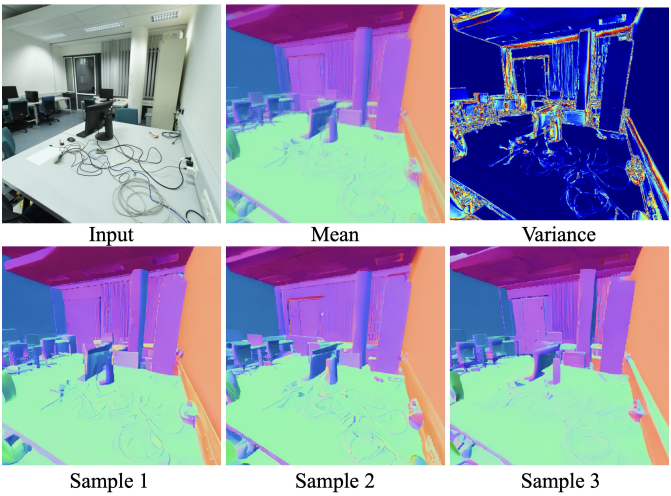
이러한 현상은 두 가지 요인에 기인한다.
- 극단적인 조명, 극적인 카메라 움직임, 모션 블러, 저화질 이미지와 같은 불안정한 이미징 조건.
- Diffusion process의 stocasticity는 가능한 한 deterministic해야 하는 추정 과정의 본질과 모순된다.
Normal 추정은 depth 추정보다 더 deterministic하기 때문에 diffusion process의 내재적 확률성을 완하하는 것이 더 중요하다. 그러나 diffusion process에서 stocasticity를 제거하면 고주파 디테일의 복원력이 저하되고 지나치게 매끄러운 normal이 생성될 수 있다. 따라서 안정성과 선명도 사이의 균형을 찾는 것이 필요하다.
본 논문은 이러한 상충 관계를 해결하기 위한 StableNormal을 제시하였다. StableNormal은 안정적인 초기화와 안정적인 정제가 정확하고 안정적인 normal 추정값을 생성하는 데 필수적임을 보여준다. StableNormal은 coarse-to-fine 체계를 따른다.
- 안정적인 초기화를 위한 one-step normal 추정
- Semantic을 기반으로 점진적으로 normal map을 선명하게 정제
구체적으로, Shrinkage Regularizer를 도입하여 one-step normal 추정 모델을 학습시키는데, 이는 원래 diffusion loss를 생성 항과 재구성 항으로 분할하여 학습 분산을 줄인다. YOSO (You-Only-Sample-Once)라 부르는 이 one-step 추정 모델은 이미 SOTA 모델과 동등한 성능을 보인다. 또한, DINOv2 semantic prior를 통합하여 diffusion 기반 정제 과정의 안정성을 향상시키기 위해 Semantic-Guided Diffusion Refinement Network (SG-DRN)를 제시하였다. Semantic prior는 로컬 디테일을 향상시키면서 표본 분산을 감소시킨다.
Method
1. Diffusion-based Normal Estimator
Normal Estimation with SD
Normal 추정은 RGB 이미지를 normal map 이미지로 변환하는 것으로 볼 수 있으므로 SD에서 diffusion prior를 효과적으로 활용할 수 있다. 간단한 접근 방식은 RGB 이미지를 컨디셔닝 신호로 사용하여 해당 normal map을 생성하는 것이다. 더 구체적으로, 컨디셔닝 신호는 먼저 RGB 입력 이미지 $I$를 사전 학습된 VAE 인코더 $\textrm{En}$을 사용하여 latent code로 인코딩한 다음 ControlNet과 유사하게 이 latent code를 추가 인코더 $f_\phi$를 통해 U-Net 디코더 블록에 대한 제어 신호로 변환한다. U-Net의 디코더 블록과 인코더 $f_\phi$는 다음과 같은 loss로 학습된다 ($\epsilon$-reparameterization).
\[\begin{equation} L_{\theta, \phi} = \mathbb{E}_{\epsilon, c, I, t} \| \epsilon - \mu_\theta^{\epsilon} (x_t, c, t, f_\phi (\textrm{En}(I))) \|^2 \end{equation}\]($I$는 입력 이미지, $x_t = q(\textrm{En}(N_\textrm{gt}))$는 GT normal map $N_\textrm{gt}$에서 인코딩된 timestep $t$에서의 latent feature)
Inference 시에는 학습된 diffusion model에 대해 샘플링 알고리즘을 실행하여 주어진 RGB 이미지의 normal map을 간단하게 추정할 수 있다. 추정된 normal map은 보기에는 선명해 보이지만, stocastic하게 생성된다. 추정된 normal map의 높은 분산은 일반적으로 해당 입력 이미지와 정렬되지 않는다. 여러 결과의 평균화을 취하는 앙상블 방식을 사용할 수 있지만, 결과는 여전히 만족스럽지 않으며 전체 앙상블 과정에 상당한 시간이 소요된다.
The Variance from the Diffusion Model
Diffusion 기반 normal 추정의 주요 문제는 inference 절차의 높은 분산이다. Diffusion 샘플링 알고리즘의 무작위성 원인은 대부분 초기 Gaussian noise와 중간에 주입된 모든 Gaussian noise이다. 본 논문은 2단계 inference 방식을 통해 분산을 완화할 것을 제안하였다. 초기 단계에서는 높은 확실성을 가진 신뢰할 수 있는 초기 추정값이 생성된다. 이후, 제한된 수의 diffusion 샘플링 step을 사용하여 결과를 조정하고, Gaussian noise 주입을 최소화한다.
2. You-Only-Sample-Once Normal Initialization
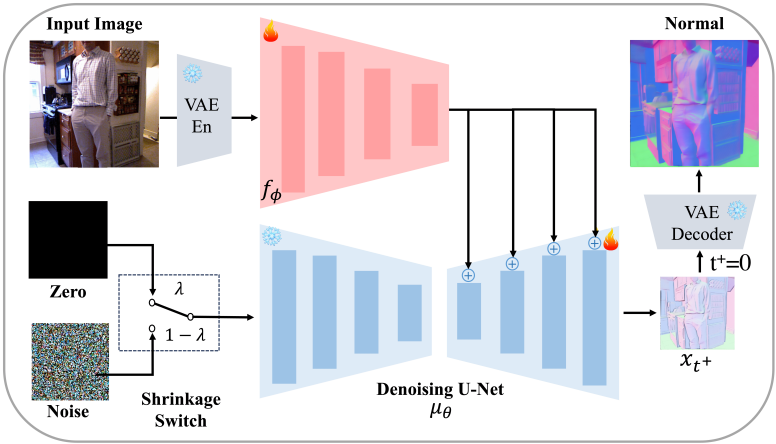
One-step Estimation
Normal 추정을 위한 one-step 샘플링 전략은 GenPercept에 처음 도입되었다. GenPercept은 Gaussian noise를 도입하지 않아 추정 결과가 deterministic하지만 출력이 over-smoothing되는 단점이 있다. 대신, 본 논문은 선명도와 안정성의 균형을 맞추기 위해 Gaussian noise 입력을 사용하여 one-step 샘플링을 수행한다. 수학적으로, $x_0$-parameterization 대신 $x_{t^{+}}$-parameterization을 채택하고, loss function을 다음과 같이 재구성한다.
\[\begin{equation} L_{\theta, \phi} = \mathbb{E}_{x_{t^{+}}, c, I, t^{+}} \| x_{t^{+}} - \mu_\theta^{x_{t^{+}}} (x_\infty, c, t^{+}, f_\phi (\textrm{En}(I))) \|^2 \end{equation}\]($x_\infty$ $t$가 무한대에 접근하는 forward diffusion process를 실행하여 생성된 Gaussian 분포의 noise 샘플)
여기서는 시간 $t = 0$이 아닌 시간 $t^{+} \in (0,T)$에 해당하는 Gaussian 일대일 분포를 매핑하는 데 관심이 있다. 이러한 one-step 추정을 You-Only-Sample-Once (YOSO)라고 부른다. 안타깝게도 Gaussian 분포에서 $x_{t^{+}}$를 단순하게 추정하는 것은 다대일 매핑을 학습하는 것을 의미하며, 이는 어렵다. 이 문제를 해결하기 위해 Shrinkage Regularizer를 사용한다.
Shrinkage Regularizer
정규화된 loss로 diffusion model을 학습시켜 예측된 normal map의 분산을 더욱 줄인다. 일반적으로 어려운 예측 분포의 엔트로피에 페널티를 주는 대신, 예측된 normal map의 분포 \(\mu_\theta^{x_{t^{+}}} (x_\infty, c, t, f_\phi (\textrm{En}(I)))\)를 디랙 델타 함수 \(\delta (x - \mu_\theta^{x_{t^{+}}} (0, c, t, f_\phi (\textrm{En}(I))))\)로 축소시킨다.
\[\begin{equation} L_{\theta, \phi} = \begin{cases} \mathbb{E}_{x_{t^{+}}, c, I, t^{+}} \| x_{t^{+}} - \mu_\theta^{x_{t^{+}}} (x_\infty, c, t, f_\phi (\textrm{En}(I))) \|^2 & \textrm{if} \; p \ge \lambda \\ \mathbb{E}_{x_{t^{+}}, c, I, t^{+}} \| x_{t^{+}} - \mu_\theta^{x_{t^{+}}} (0, c, t, f_\phi (\textrm{En}(I))) \|^2 & \textrm{if} \; p < \lambda \end{cases} \\ \textrm{where} \quad p \sim U(0, 1), \; \lambda = 0.4 \end{equation}\]3. Semantic-guided Normal Refinement
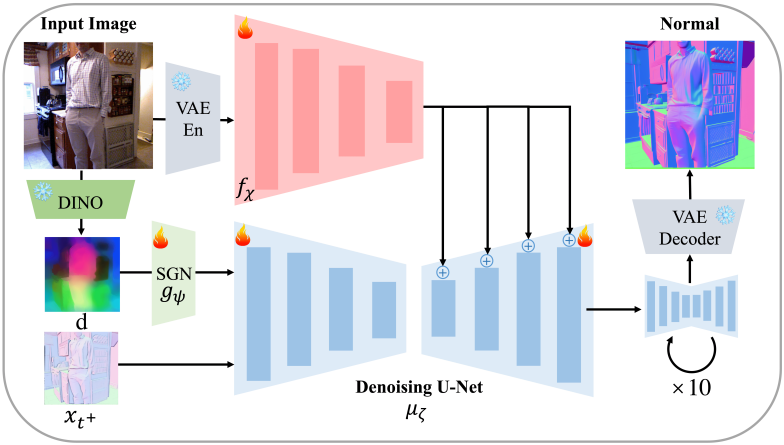
초기 normal 추정값을 개선하는 후속 샘플링 단계에서, 이미지 조건 diffusion model은 RGB 이미지 입력의 글로벌 정보 대신 로컬 정보를 활용하는 경향이 있다. 그러나 직관적으로 로컬 이미지 정보에만 의존해서는 안 된다. 예를 들어, 벽에 해당하는 픽셀의 normal을 결정할 때 글로벌 정보가 일반적으로 훨씬 더 많은 정보를 제공한다. 따라서 사전 학습된 DINOv2의 semantic feature를 보조 조건 신호로 포함한다.
Architecture of SG-DRN
SG-DRN의 아키텍처는 YOSO와 유사한 네트워크 아키텍처를 사용하며, U-Net 인코더 레이어 \(\mu_\zeta\)에 semantic feature를 주입하는 매우 가벼운 semantic-injection 네트워크 \(g_\psi\)를 제외하고는 YOSO와 유사하다.
Semantic-injection Network
효율성을 위해 U-Net에 semantic feature를 입력하는 경량 네트워크를 사용한다. 구체적으로, 이 네트워크는 조건 인코더와 유사한 4개의 conv layer를 사용하여 DINOv2 feature의 공간 해상도를 noise가 더해진 latent feature의 공간 해상도와 일치시킨다. DINOv2 feature는 일반적으로 diffusion latent feature보다 해상도가 낮기 때문에, 해상도 일치를 위해 FeatUp과 bi-linear interpolation을 사용하여 DINOv2 feature를 업샘플링한다. Noise가 더해진 latent feature는 정렬된 DINOv2 feature와 더해진 후, denoising U-Net에 입력된다. 학습 과정에서 네트워크 가중치는 Gaussian 분포를 사용하여 초기화되지만, 최종 projection layer는 zero convolution으로 초기화된다.
Loss function
I2VGen-XL을 따라 \(\mu_\zeta\)에 $x_0$-reparameterization를 적용한다. \(\mu_\zeta\)의 loss function은 다음과 같이 정의할 수 있다.
\[\begin{equation} L_{\theta, \chi, \psi} = \mathbb{E}_{x_0, c, I, d, t} \| x_0 - \mu_\zeta^{x_0} (x_t, c, t, f_\chi (\textrm{En} (I)), g_\psi (d)) \|^2 \end{equation}\]($d$는 처리된 DINOv2 semantic feature)
4. Heuristic Denoising Sampling
Inference 과정에서는 DDIM을 적용하여 최종 normal 예측값을 구한다. 구체적으로, YOSO에서 예측된 초기 normal latent \(x_{t^{+}}\)는 10-step DDIM을 통해 solver에 입력된다. 저자들은 경험적으로 초기 샘플링 step $t^{+}$를 401로 설정했으며, 이는 안정성과 선명도 간의 최적의 절충안을 제공한다.
\[\begin{aligned} x_{t-1} &= \sqrt{\alpha_{t-1}} \cdot (\hat{x}_0) + \textrm{direction} (x_t) + \tau \epsilon \\ \hat{x}_0 &= \mu_\zeta^{x_0} \left( x_t, c, t, f_\chi (\textrm{En}(I)), g_\psi (d) \right) \\ x_{t^{+}} &= \mu_\theta^{x_{t^{+}}} \left( x_\infty, c, t^{+}, f_\phi (\textrm{En} (I)) \right) \end{aligned}\]Experiments
- 구현 디테일
- base model: Stable Diffusion V2.1
- optimizer: AdamW
- learning rate: $3 \times 10^{-5}$
1. Comparison to the state-of-the-art
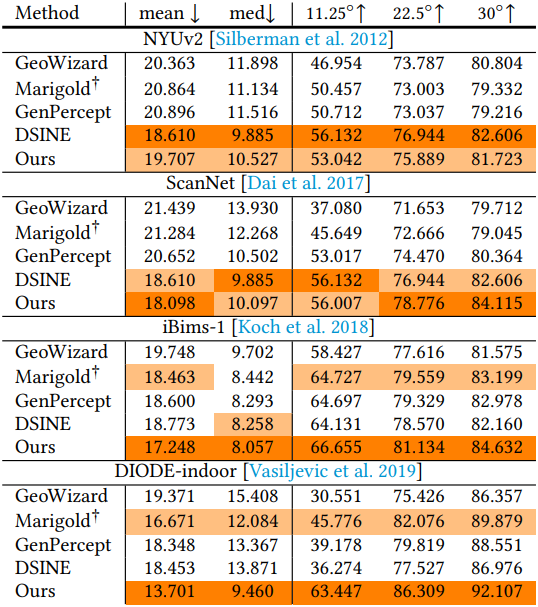
다음은 4가지 실내 벤치마크에 대한 비교 결과이다.

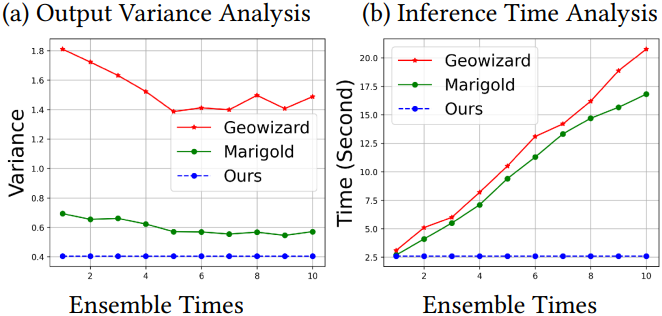
다음은 (왼쪽) 출력의 분산과 (오른쪽) inference 시간을 비교한 결과이다.
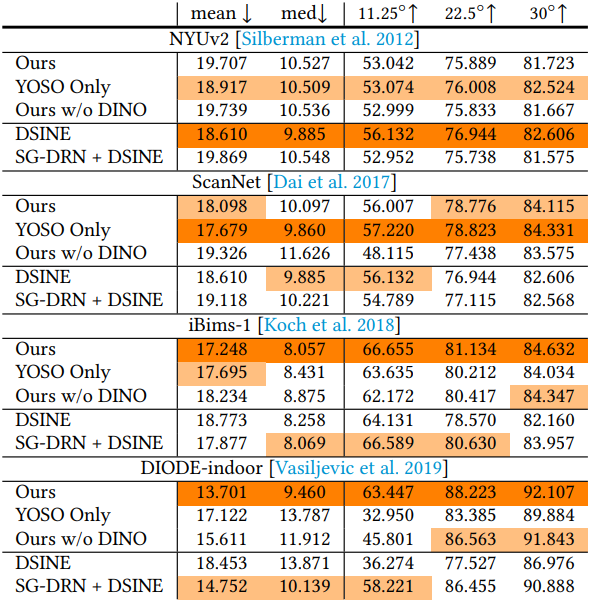
2. Ablation study
다음은 ablation 결과이다.

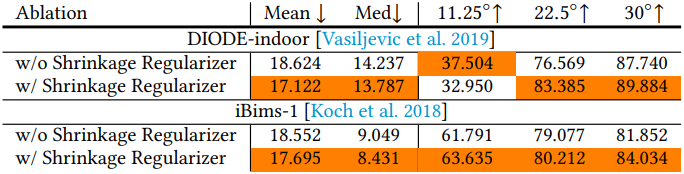
다음은 Shrinkage Regularizer에 대한 ablation 결과이다.
3. Applications
다음은 멀티뷰 표면 재구성에 대한 비교 결과이다.


다음은 monocular 표면 재구성에 대한 비교 결과이다. (DiLiGenT 데이터셋)
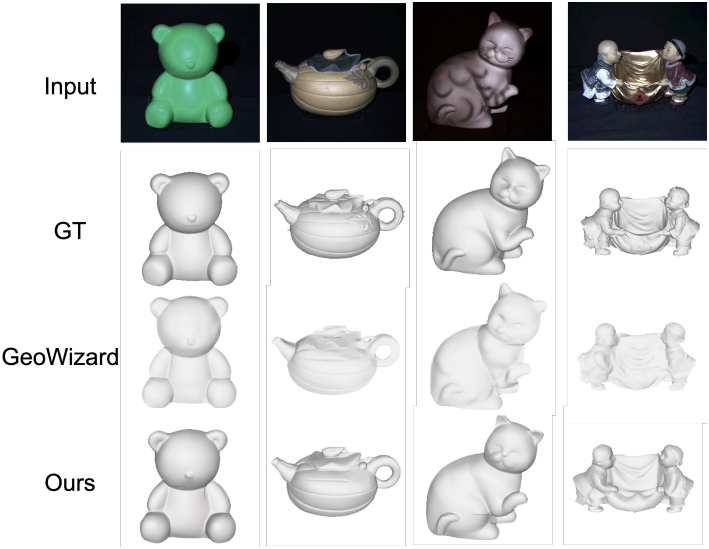

다음은 Wonder3D에 StableNormal을 적용하여 normal map의 디테일을 개선한 예시이다.
