[논문리뷰] Detection Transformer with Stable Matching (Stable-DINO)
ICCV 2023. [Paper] [Page]
Shilong Liu, Tianhe Ren, Jiayu Chen, Zhaoyang Zeng, Hao Zhang, Feng Li, Hongyang Li, Jun Huang, Hang Su, Jun Zhu, Lei Zhang
Tsinghua University | International Digital Economy Academy (IDEA) | Alibaba Group | The Hong Kong University of Science and Technology | South China University of Technology
10 Apr 2023
Introduction
Object detection은 다양한 응용 분야에서 비전의 기본 task이다. 지난 수십 년 동안 딥러닝, 특히 CNN의 발전으로 큰 진전이 있었다.
Detection Transformer (DETR)은 새로운 Transformer 기반 object detector를 제안하여 연구 커뮤니티에서 많은 관심을 끌었다. 모든 수작업 모듈이 필요하지 않으며 end-to-end 학습이 가능하다. DETR의 핵심 디자인 중 하나는 Hungarian matching을 사용하여 ground truth 레이블에 예측을 일대일 할당하는 매칭 전략이다. 새로운 디자인에도 불구하고 DETR에는 느린 수렴과 낮은 성능을 포함하여 이 혁신적인 접근 방식과 관련된 특정 제한 사항이 있다. 많은 후속 연구들에서는 위치 prior, 추가 positive example들, 효율적인 연산자의 도입과 같은 다양한 관점에서 DETR을 개선하려고 노력했다. 많은 최적화를 통해 DINO는 COCO detection 순위표에서 새로운 기록을 세웠으며 Transformer 기반 방법이 대규모 학습을 위한 주류 detector가 되었다.
DETR-like detector는 인상적인 성능을 달성하지만 현재까지 충분히 주목받지 못한 중요한 문제 중 하나는 모델의 학습 안정성을 잠재적으로 손상시킬 수 있다는 것이다. 이 문제는 다양한 디코더 레이어 간의 불안정한 매칭 문제와 관련이 있다. DETR-like 모델은 Transformer 디코더에 여러 디코더 레이어를 쌓는다. 모델은 각 디코더 레이어 이후에 예측을 할당하고 loss를 계산한다. 그러나 이러한 예측에 할당된 레이블은 레이어마다 다를 수 있다. 이러한 불일치는 각 ground truth 레이블이 하나의 예측과만 일치하는 DETR 변형의 일대일 매칭 전략에 따라 최적화 대상 충돌로 이어질 수 있다.
현재까지 불안정한 매칭 문제를 해결하려고 시도한 연구는 단 하나뿐이다. DN-DETR은 불일치를 방지하기 위해 추가로 hard-assigned query를 도입하여 새로운 denoising 학습 접근 방식을 제안했다. 일부 다른 연구들에서는 더 빠른 수렴을 위해 추가 query를 추가했지만 불안정한 매칭 문제에 중점을 두지 않았다. 이에 비해 본 논문은 매칭 및 loss 계산 과정에 중점을 두어 이 문제를 해결한다.
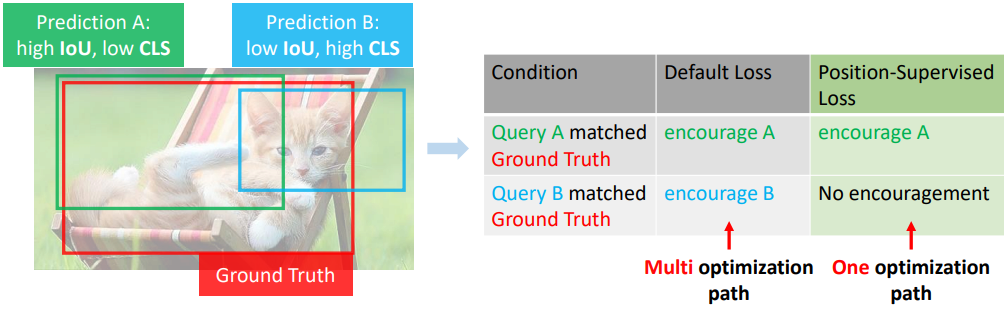
불안정한 매칭 문제의 핵심은 다중 최적화 경로 문제이다. 위 그림에서 볼 수 있듯이 학습 중에 두 가지 불완전한 예측이 있다. 예측 A는 IoU 점수가 더 높지만 분류 점수는 더 낮다. 반면 예측 B는 그 반대이다. 이는 학습 중에 가장 간단하지만 가장 일반적인 경우이다. 모델은 그 중 하나를 ground truth에 할당하여 두 가지 최적화 기본 설정을 생성한다. 하나는 더 나은 분류 결과를 얻기 위해 높은 위치 메트릭을 사용하여 A를 장려하고, 다른 하나는 더 나은 IoU 점수를 얻기 위해 높은 semantic 메트릭 (여기서는 분류 점수)을 사용하여 B를 장려한다. 이러한 기본 설정을 다양한 최적화 경로라고 한다. 학습 중 랜덤성으로 인해 각 예측은 positive example로 할당되고 다른 예측은 negative example로 간주될 확률이 있다. 기본 loss 디자인이 주어지면 A 또는 B가 positive example로 선택되는지 여부에 관계없이 모델은 ground truth bounding box와의 정렬을 향해 이를 최적화한다. 이는 위 그림의 오른쪽 표에 표시된 것처럼 모델에 다중 최적화 경로가 있음을 의미한다. 이 문제는 여러 query가 positive example로 선택되므로 기존 detector에서는 덜 중요하다. 그러나 DETR-like 모델의 일대일 매칭은 예측 A와 B 사이의 최적화 격차를 확대하여 모델 학습 효율성을 떨어뜨린다.
문제를 해결하기 위해 가장 중요한 디자인은 위치 메트릭 (ex. IOU)을 사용하여 positive example의 분류 점수를 supervise하는 것이다. 분류 점수를 제한하기 위해 위치 정보를 사용하는 경우 예측 B는 IoU 점수가 낮기 때문에 일치하더라도 권장되지 않는다. 결과적으로 하나의 최적화 경로만 사용할 수 있어 다중 최적화 경로 문제가 완화된다. 추가 분류 점수 관련 supervision이 도입되면 예측 B의 분류 점수가 더 높기 때문에 다중 최적화 경로는 여전히 모델 성능을 저하시킨다. 이 원칙을 통해 loss와 매칭 비용에 대한 두 가지 간단하지만 효과적인 수정, 즉 position-supervised loss와 position-modulated cost를 제안한다. 둘 다 더 빠른 수렴과 더 나은 모델 성능을 가능하게 한다. 본 논문이 제안한 접근 방식은 또한 DETR-like 모델과 기존 detector 사이의 연결을 설정한다. 둘 다 높은 위치 점수를 가진 예측이 더 나은 분류 점수를 갖도록 장려하기 때문이다.
더욱이 모델의 backbone과 인코더 feature들을 융합하면 사전 학습된 backbone feature들의 활용을 용이하게 하여 특히 초기 학습 iteration에서 수렴을 더 빠르게 하고 거의 추가 비용 없이 모델의 성능을 향상시킬 수 있다. 본 논문은 세 가지 융합 방법을 제안하고 실험을 위해 dense memory fusion을 경험적으로 선택하였다.
저자들은 여러 가지 DETR 변형에 대한 방법을 검증하였으며, 모든 실험에서 일관된 개선을 보여주었다. 그런 다음 본 논문의 방법을 DINO와 결합하여 Stable-DINO라는 강력한 detector를 구축하였다. Stable-DINO는 COCO detection 벤치마크에서 인상적인 결과를 제공하였다.
Stable Matching
1. Revisit DETR Losses and Matching Costs
대부분의 DETR 변형들은 유사한 loss와 매칭 디자인을 가지고 있다. 저자들은 SOTA 모델 DINO를 예로 사용하였다. Deformable DETR의 loss와 매칭을 상속하며 디자인은 DETR-like detector에 일반적으로 사용된다. 일부 다른 DETR-like 모델은 약간의 수정만으로 다른 디자인을 사용할 수 있다.
DINO의 최종 loss는 classification loss \(\mathcal{L}_\textrm{cls}\), box L1 loss \(\mathcal{L}_\textrm{bbox}\), GIOU loss \(\mathcal{L}_\textrm{GIOU}\)의 세 부분으로 구성된다. Box L1 loss와 GIOU loss는 객체 위치 파악에 사용되며 모델에서는 수정되지 않는다. 본 논문에서는 classification loss에 중점을 둔다. DINO는 focal loss를 classification loss로 사용한다.
\[\begin{equation} \mathcal{L}_\textrm{cls} = \sum_{i=1}^{N_\textrm{pos}} \vert 1 - p_i \vert^\gamma \textrm{BCE} (p_i, 1) + \sum_{i=1}^{N_\textrm{neg}} p_i^\gamma \textrm{BCE} (p_i, 0) \end{equation}\]여기서 $N_\textrm{pos}$와 $N_\textrm{neg}$는 positive example과 negative example의 수이고, $\textrm{BCE}$는 binary cross-entropy loss를 의미하고, $p_i$는 $i$번째 example의 예측 확률, $\gamma$는 focal loss에 대한 hyperparameter이다.
매칭 프로세스는 positive example과 negative example을 결정한다. 일반적으로 ground truth에는 positive example로 하나의 예측만 할당된다. Ground truth에 할당되지 않은 예측은 negative example로 간주된다.
Ground truth로 예측을 할당하기 위해 먼저 둘 사이의 비용 행렬 $\mathcal{C} \in \mathbb{R}^{N_\textrm{pred} \times N_\textrm{gt}}$를 계산한다. $N_\textrm{pred}$와 $N_\textrm{gt}$는 예측과 ground truth의 수이다. 그런 다음 Hungarian 매칭 알고리즘은 비용 행렬에 대해 수행하여 총 비용을 최소화하여 각 ground truth에 예측을 할당한다.
Loss function과 유사하게 최종 비용에는 classification cost \(\mathcal{C}_\textrm{cls}\), box L1 cost \(\mathcal{C}_\textrm{bbox}\), GIOU cost \(C_\textrm{GIOU}\)의 세 가지가 포함된다. 본 논문은 classification cost에만 중점을 둔다. $i$번째 예측과 $j$번째 ground truth의 경우 classification cost는 다음과 같다.
\[\begin{equation} \mathcal{C}_\textrm{cls} (i, j) = \vert 1 - p_i \vert^\gamma \textrm{BCE} (p_i, 1) - p_i^\gamma \textrm{BCE} (1 - p_i, 1) \end{equation}\]위 식은 focal cost와 유사하지만 약간의 수정이 있다. Focal loss는 positive example이 1을 예측하도록 장려하는 반면, classification cost는 positive example을 0으로 피하기 위해 추가 페널티 항을 추가한다.
2. Position-Supervised Loss
다중 최적화 문제를 해결하기 위해 positive example의 학습 확률을 감독하기 위해 위치 점수만 사용한다. 이전 연구에서 영감을 받아 classification loss를 다음과 같이 간단히 수정할 수 있다.
\[\begin{equation} \mathcal{L}_\textrm{cls}^{(\textrm{new})} = \sum_{i=1}^{N_\textrm{pos}} \vert f_1 (s_i) - p_i \vert^\gamma \textrm{BCE} (p_i, f_1 (s_i)) + \sum_{i=1}^{N_\textrm{neg}} p_i^\gamma \textrm{BCE} (p_i, 0) \end{equation}\]$s^i$를 $i$번째 ground truth와 해당 예측 사이의 IOU와 같은 위치 메트릭으로 사용한다. 몇 가지 예로 $f_1 (s_i)$를 $s_i$, $s_i^2$, $e^{s_i}$로 사용할 수 있다.
저자들은 $f_1 (s_i) = \epsilon (s_i^2)$가 가장 잘 작동한다는 것을 발견했다. 여기서 $\epsilon$은 IOU 값이 때때로 매우 작을 수 있기 때문에 일부 퇴보된 솔루션을 피하기 위해 숫자를 다시 조정하는 변환이다. 저자들은 두 가지 재조정 전략을 시도했다. 첫 번째는 학습 example에서 가능한 모든 쌍 중에서 가장 높은 $s_i^2$가 최대 IOU 값과 같도록 하는 것이다. 다른 하나는 가장 높은 $s_i^2$가 1.0과 같도록 하는 것이다. 전자는 DINO와 같이 더 많은 query (900개)가 있는 detector에 더 잘 작동하고, 후자는 300개의 query가 있는 detector에서 더 잘 작동한다.
이 디자인은 IOU와 같은 위치 메트릭을 사용하여 분류 점수를 supervise하려고 한다. 분류 점수가 낮고 IOU 점수가 높은 예측을 장려하는 반면, 분류 점수는 높지만 IOU 점수가 낮은 예측에는 페널티를 적용한다.
3. Position-Modulated Matching
Position-supervised classification loss는 IOU 점수는 높지만 분류 점수는 낮은 예측을 장려하는 것을 목표로 한다. 새로운 loss의 취지에 따라 매칭 비용에 일부 수정을 가한다.
\[\begin{equation} \mathcal{L}_\textrm{cls}^{(\textrm{new})} = \vert 1 - p_i f_2 (s_i^\prime) \vert^\gamma \textrm{BCE} (p_i f_2 (s_i^\prime), 1) - (p_i f_2 (s_i^\prime))^\gamma \textrm{BCE} (1 - p_i f_2 (s_i^\prime), 1) \end{equation}\]$s_i^\prime$는 GIOU의 범위가 $[-1, 1]$이기 때문에 $[0, 1]$ 범위로 이동하고 크기를 조정한 위치 메트릭이다. $f_2$는 튜닝할 또 다른 함수이다. 저자들은 구현에서 경험적으로 $f_2 (s_i^\prime) = (s_i^\prime)^{0.5}$를 사용한다.
직관적으로, $f_2 (s_i^\prime)$는 부정확한 예측 상자를 사용하여 예측의 가중치를 낮추기 위한 변조된 함수로 사용된다. 분류 점수와 bounding box 예측을 더 잘 정렬하는 데도 도움이 된다.
흥미로운 질문 중 하나는 왜 새로운 classification loss를 새로운 classification cost로 직접 사용하지 않는가이다. 매칭은 모든 예측과 ground truth 사이에서 계산되며, 그 아래에는 품질이 낮은 예측이 많이 있다. 이상적으로는 IOU 점수가 높고 분류 점수가 높은 예측이 매칭 비용이 낮기 때문에 positive example로 선택되기를 바란다. 그러나 IOU 점수와 분류 점수가 낮은 예측도 매칭 비용이 낮아 모델이 퇴화된다.
4. Analyses
위치 점수만으로 분류를 supervise하는 이유는 무엇인가?

저자들은 불안정한 매칭의 원인이 다중 최적화 경로 문제라고 주장한다. 가장 간단한 시나리오에 대해 논의하자. 두 개의 불완전한 예측 A와 B가 있다. 위 그림에 표시된 것처럼 예측 A는 IOU 점수가 더 높지만 중심이 배경에 있기 때문에 분류 점수가 더 낮다. 이와 대조적으로 예측 B는 분류 점수가 더 높지만 IOU 점수는 더 낮다. 두 가지 예측은 실제 개체를 놓고 경쟁한다. 하나가 positive example로 할당되면 다른 하나는 negative example로 설정된다. 두 개의 불완전한 후보가 포함된 ground truth는 학습 중에, 특히 초기 step에서 흔히 발생한다.
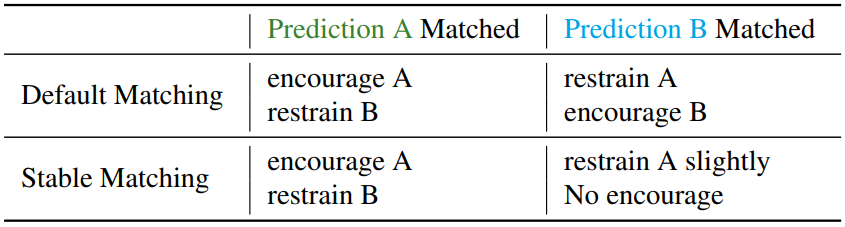
학습 중 랜덤성으로 인해 두 예측 중 각각은 positive example로 할당될 확률이 있다. 기본 DETR 변형 loss 디자인에서는 위 표와 같이 기본 loss 디자인이 positive example을 장려하고 negative example을 제한하므로 각 가능성이 증폭된다. Detection 모델에는 두 가지 다른 최적화 경로가 있다. 모델은 IOU가 높은 샘플을 선호하거나 분류 점수가 높은 샘플을 선호한다. 다양한 최적화 경로는 학습 중에 모델을 혼란스럽게 할 수 있다. 좋은 질문은 모델이 두 가지 예측을 모두 장려할 수 있는지 여부이다. 불행히도 이는 일대일 매칭 요구 사항을 위반하게 된다. 각 ground truth에 여러 예측을 할당하는 기존 detector에서는 문제가 중요하지 않다. DETR-like 모델의 일대일 매칭 전략은 충돌을 증폭시킨다.
대조적으로, IOU와 같은 위치 메트릭을 사용하여 분류 점수를 감독하면 위 표의 하단 행에 표시된 것처럼 문제가 제거된다. 예측 A만 권장되며, 예측 B가 일치하면 IOU 점수가 낮기 때문에 지속적으로 최적화되지 않는다. 모델에 대한 최적화 경로는 하나만 있으며 이를 통해 학습이 안정적으로 이루어진다.
분류 점수를 감독하기 위해 분류 정보를 사용하는 것은 어떠한가? 기존 detector의 일부 이전 연구들에서는 분류 점수와 IOU 점수의 조합인 품질 점수를 사용하여 분류 점수와 IOU 점수를 정렬하려고 시도했다. 불행하게도 이 디자인은 불안정한 매칭, 다중 최적화 경로 문제의 근본 원인을 해결할 수 없기 때문에 DETR-like 모델에는 적합하지 않다. 분류 점수와 IOU 점수가 모두 타겟에 포함되어 있다고 가정하자. 이 경우 예측 B도 분류 점수가 높으므로 일치하면 권장된다. 모델 학습을 손상시키는 다중 최적화 경로 문제도 존재한다.
또 다른 직접적인 질문은 모델을 다른 경로로 최적화할 수 있는지 여부이다. 높은 분류 점수를 선호하도록 모델을 가이드하려는 경우 (즉 예측 B를 권장), 동일한 카테고리에 두 개의 객체가 있는 경우 모호성이 발생한다. 예를 들어, 위 그림에 고양이 두 마리가 있다. 분류 점수는 semantic 정보에 따라 결정된다. 즉, 고양이 근처의 상자는 분류 점수가 높기 때문에 모델 학습에 손상을 줄 수 있다.
Detection Transformer에서 분류 점수의 역할 재고
새로운 매칭 loss는 DETR-like 모델을 기존 detector에 연결한다. 새로운 loss 디자인은 기존 detector와 유사한 최적화 경로를 공유한다.
Object detector에는 두 가지 최적화 경로가 있다. 하나는 좋은 예측 상자를 찾아 분류 점수를 최적화하는 것이고, 다른 하나는 분류 점수가 높은 예측을 ground truth 상자에 최적화하는 것이다. 대부분의 기존 detector는 위치 정확도만 확인하여 예측을 할당한다. 모델은 실제값에 가까운 anchor box를 권장한다. 이는 대부분의 전통적인 detector가 첫 번째 최적화 방법을 선택한다는 것을 의미한다. 이와 달리 DETR-like 매칭은 분류 점수를 추가로 고려하고 분류 점수와 localization 점수의 가중 합을 최종 비용 행렬로 사용한다. 새로운 매칭 방법으로 인해 두 가지 방법 간에 충돌이 발생한다.
그 이후에도 DETR-like 모델이 학습 중에 분류 점수를 사용하는 이유는 무엇인가? 저자들은 오히려 일대일 매칭을 하기에는 꺼려지는 디자인에 가깝다고 주장한다. 이전 연구에서는 classification cost를 도입하는 것이 일대일 매칭의 핵심이라는 것을 보여주었다. 이는 ground truth에 대한 단 하나의 positive example만을 보장할 수 있다. Localization loss (box L1 loss, GIOU loss)는 negative example을 제한하지 않으므로 ground truth에 가까운 모든 예측은 ground truth를 향해 최적화된다. 매칭 시 위치 정보만 고려하면 불안정한 결과가 발생한다. 매칭에서 분류 점수를 사용하면 분류 점수를 어떤 예측을 positive example로 사용해야 하는지 나타내는 표시로 사용하므로 위치만 사용한 매칭에 비해 학습 중에 안정적인 매칭이 보장된다.
그러나 분류 점수는 위치 정보와의 상호 작용 없이 독립적으로 최적화되므로 때로는 모델을 다른 최적화 경로로 유도한다. 즉, 분류 점수는 더 높지만 IOU 점수는 더 낮은 상자를 권장한다. 본 논문의 position-supervised loss는 분류와 localization을 정렬하는 데 도움이 될 수 있으며, 이는 일대일 매칭을 보장할 뿐만 아니라 다중 최적화 문제도 해결한다.
새로운 loss로 인해 DETR-like 모델은 둘 다 더 큰 IOU 점수로 예측을 장려하지만 더 나쁜 분류 점수로 예측을 장려하므로 기존 detector와 더 유사하게 작동한다.
불안정한 점수의 비교
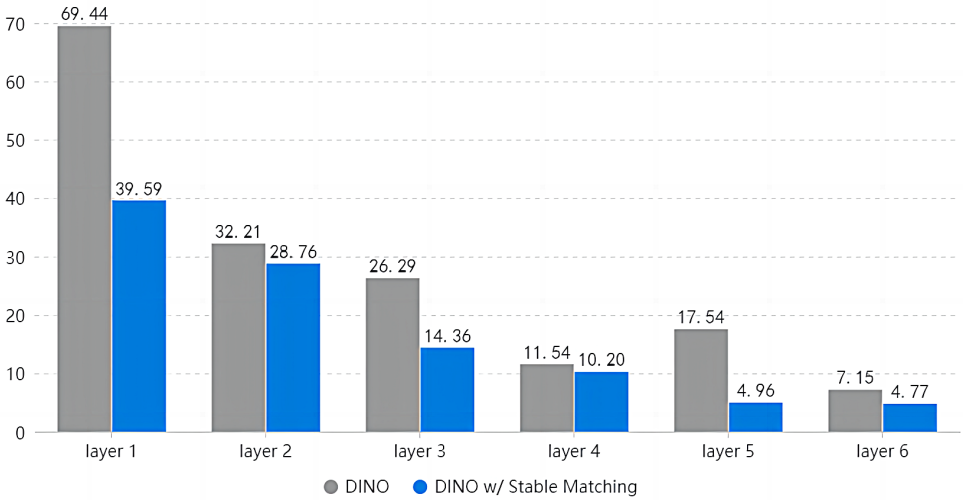
본 논문의 방법의 효율성을 확인하기 위해 위 그래프에서 바닐라 DINO와 안정적인 매칭을 사용하는 DINO 사이의 불안정한 점수를 비교하였다. 불안정한 점수는 인접한 디코더 레이어 간의 일치하지 않는 매칭 결과이다. 예를 들어, 이미지에 10개의 ground truth 상자가 있고 단 하나의 상자에만 $(i − 1)$번째 레이어와 $i$번째 레이어에서 일치하는 다른 예측 인덱스가 있는 경우 레이어 $i$의 불안정한 점수는 $1/10 = 10.00\%$이다. 일반적으로 모델에는 6개의 디코더 레이어가 있다. 레이어 1의 불안정한 점수는 인코더와 첫 번째 디코더 레이어의 매칭 결과를 비교하여 계산한다.
저자들은 5000번째 step의 모델 체크포인트를 사용하고 COCO val2017 데이터셋의 처음 20개 이미지에 대한 모델을 평가하였다. 결과는 본 논문의 모델이 DINO보다 더 안정적이라는 것을 보여준다. 위 그래프에는 두 가지 흥미로운 관찰이 있다.
- 불안정한 점수는 일반적으로 첫 번째 디코더 레이어에서 마지막 디코더 레이어로 감소한다. 이는 더 인덱스가 큰 디코더 레이어가 더 안정적인 예측을 가질 수 있음을 의미한다.
- DINO의 불안정한 점수 중 레이어 5에는 이상한 피크가 있는 반면, 안정적인 매칭을 사용한 DINO는 그렇지 않다. 이는 랜덤성이 피크를 유발하는 것으로 의심된다.
Memory Fusion
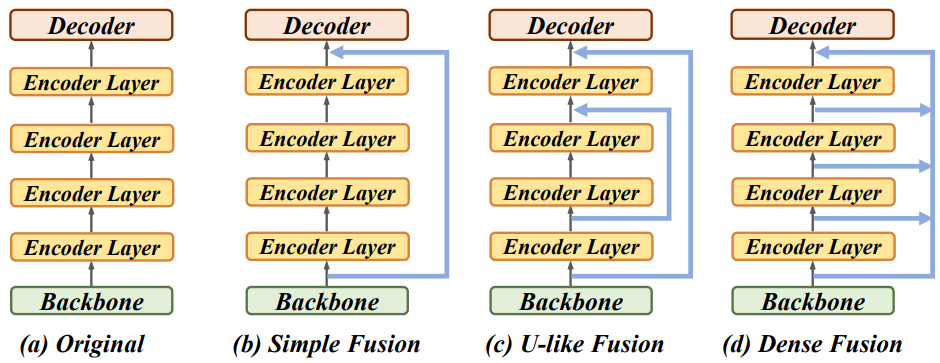
초기 학습 단계에서 모델 수렴 속도를 더욱 향상시키기 위해 본 논문은 다양한 수준의 인코더 출력 feature들을 멀티스케일 backbone feature와 병합하는 memory fusion이라는 간단한 feature 융합 기술을 제안했다. 저자들은 위 그림의 (b), (c), (d)에 표시된 simple fusion, U-like fusion, dense fusion이라는 세 가지 memory fusion 방식을 제안한다. 여러 feature들을 융합하려면 먼저 feature 차원을 따라 feature들을 concat한 다음 concat된 feature을 원래 차원에 project한다.
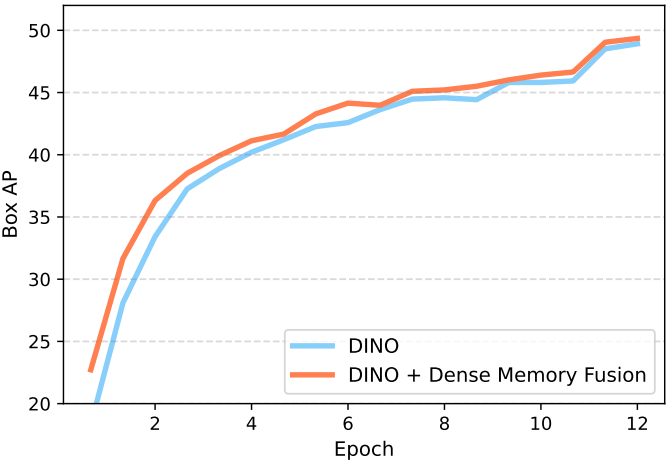
Dense fusion은 더 나은 성능을 달성하며, 실험에서 기본 feature fusion으로 사용된다. 위 그림은 DINO와 dense fusion을 사용한 DINO의 학습 곡선을 비교한 그래프이다. 이는 융합이 특히 초기 단계에서 더 빠른 수렴을 가능하게 함을 보여준다.
Experiments
- 데이터셋: COCO 2017 object detection
- 구현 디테일
- optimizer: AdamW
- learning rate: $1 \times 10^{-4}$ (12 epochs 유지 후 11 epochs 마다 0.1배)
- weight decay: $1 \times 10^{-4}$
- hyperparameter는 DETR 변형들과 동일하게 사용
- classification loss 가중치: 6.0
- NMS threshold: 0.8
1. Main Results
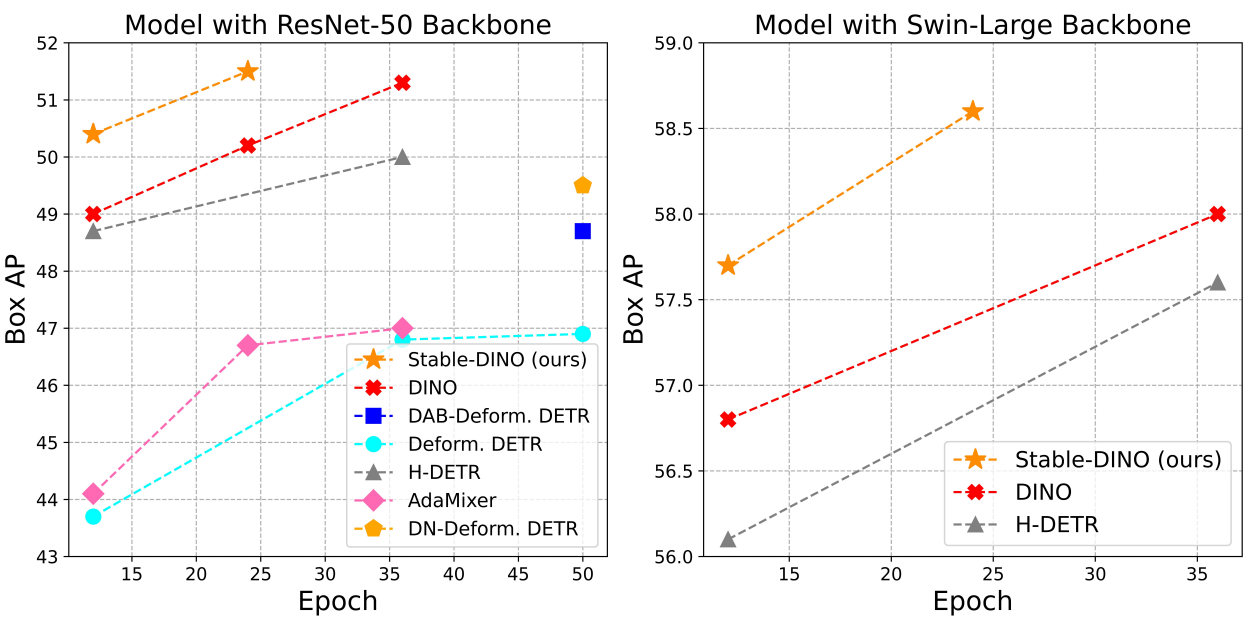
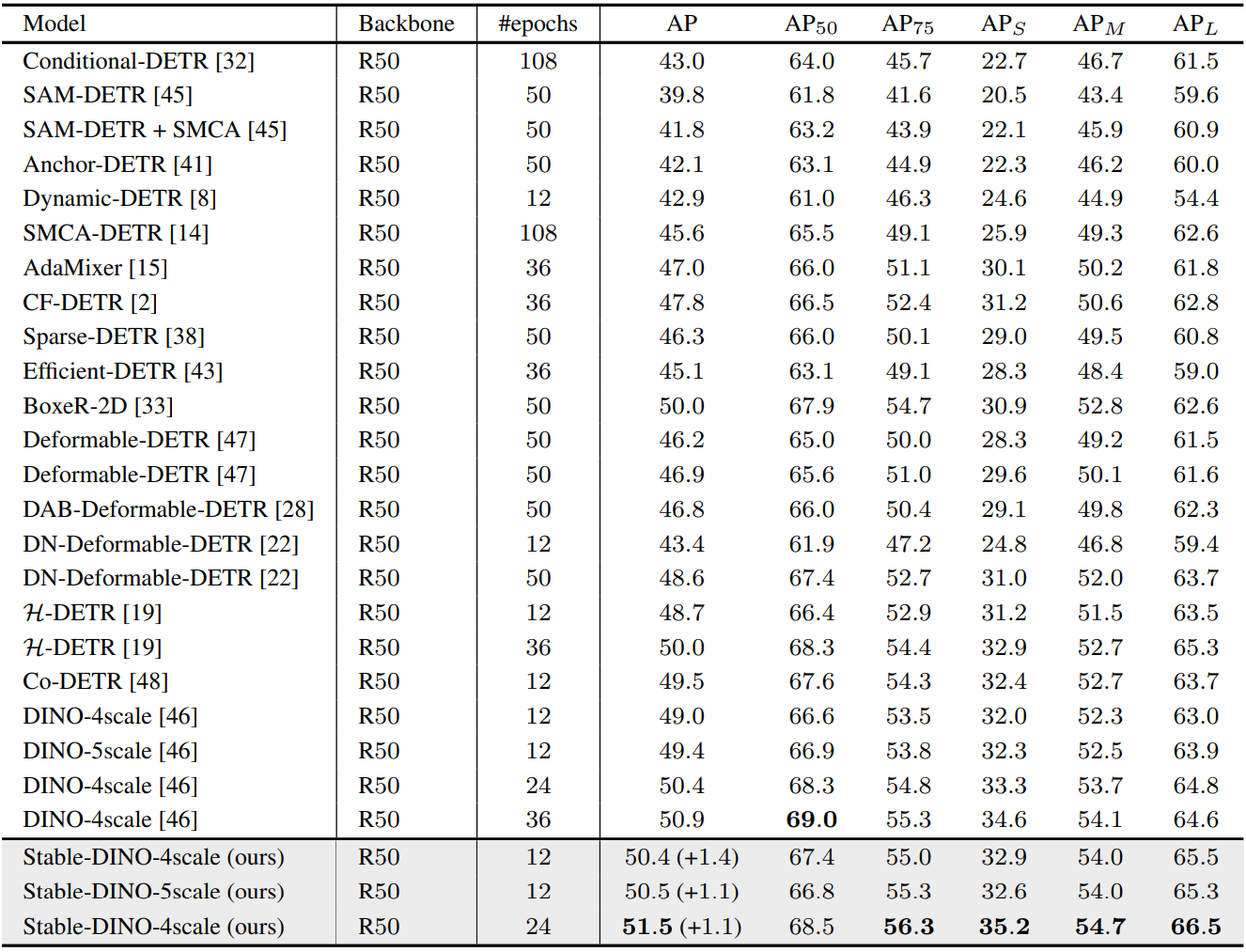
다음은 COCO val2017에서 ResNet-50 backbone을 사용하는 이전 DETR 변형들과 비교한 표이다.
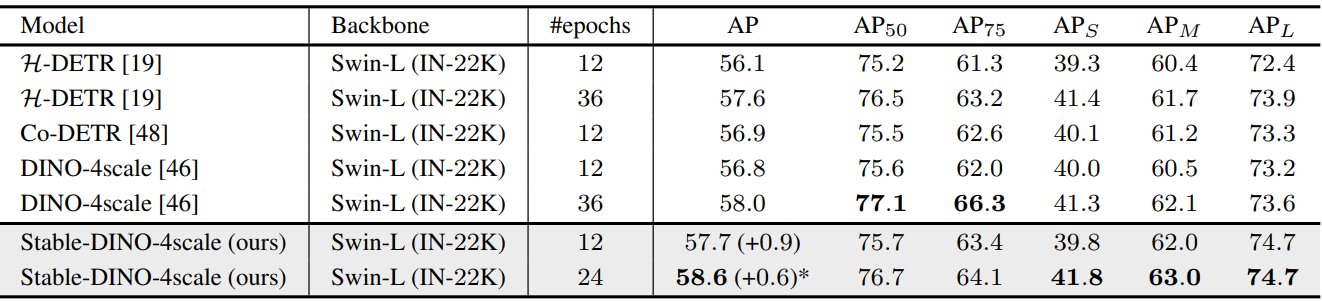
다음은 COCO val2017에서 Swin-L backbone을 사용하는 이전 DETR 변형들과 비교한 표이다.
다음은 COCO val2017에서 SOTA instance segmentation 모델과 Stable-MaskDINO를 비교한 표이다.

2. Generalization of our Methods
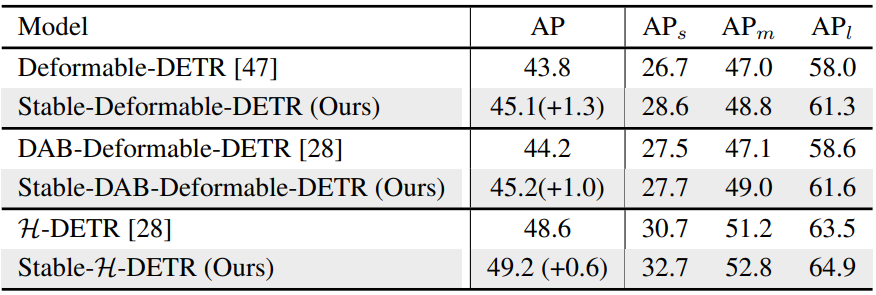
다음은 다른 DETR 변형들에 대한 본 논문의 방법의 효과를 비교한 표이다.
3. Ablation Study
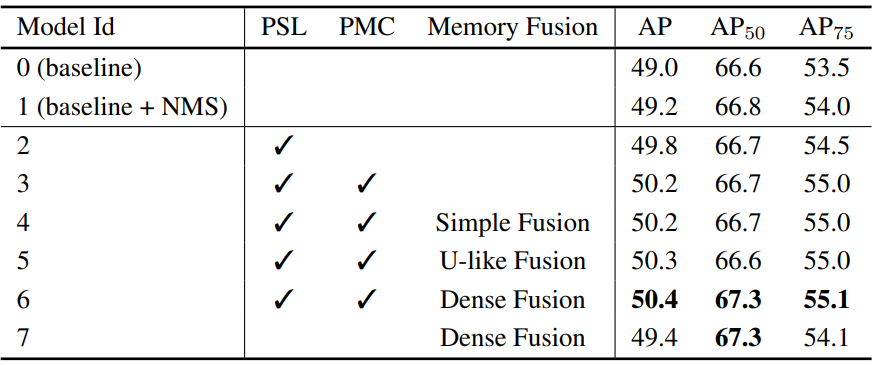
다음은 다양한 구성에 대한 ablation 결과이다. PSL은 position-supervised loss, PMC는 position-modulated cost를 의미한다.
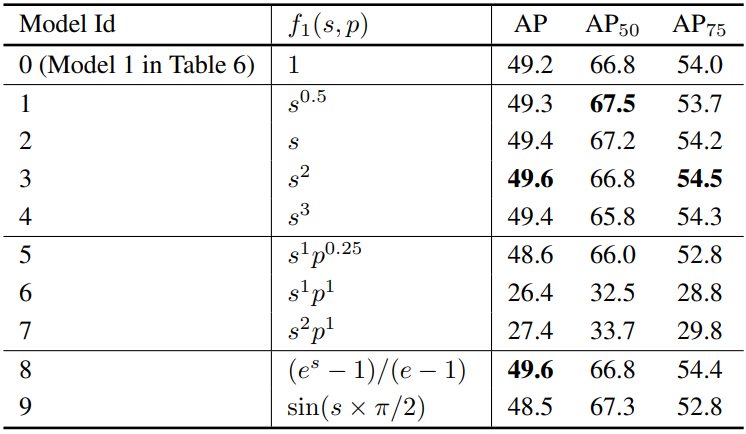
다음은 position-supervised loss에 대한 다양한 loss 디자인을 비교한 표이다. $s$와 $p$는 각각 IOU 점수와 분류 확률을 의미한다.
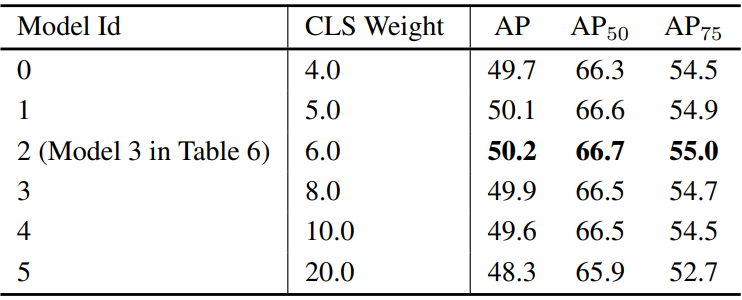
다음은 position-supervised loss에 대한 다양한 loss 가중치를 비교한 표이다.
다음은 position-modulated cost에 대한 다양한 디자인과 가중치를 비교한 표이다. $s$는 IOU 점수를 의미한다.